基于CFD的方柱繞流水動力數值模擬
劉志江,郭建廷,孟小峰,劉浩然
(1. 華中科技大學 船舶與海洋工程學院,湖北 武漢 430074;2. 江蘇科技大學 船舶與海洋工程學院,江蘇 鎮江 212000)
0 引 言
出于減噪的目的,一些船舶設置有自循環系統,利用船舶航行時迎流面所產生的動壓頭抽吸海水,降低冷凝器的用水量減少水泵的運行次數[1-2]。然而在系統與海水連通處,為防止各種雜物進入系統管道,通常在入口處設置格柵,當自循環系統工作時,海水流經格柵會產生剪切層分離等現象,從而在格柵表面及附近流場產生強大的壓力脈動場,分析格柵的壓力脈動特性,對船舶降噪具有重大意義。
本文基于計算流體力學(CFD)分析方法,在不同雷諾數Re、不同長寬比L/B下進行數值模擬,分析單方柱[3-4]的主要繞流參數和壓力脈動的變化規律。在此基礎上,取定截面長寬比,分析雷諾數以及間距比對多方柱[5-6]繞流參數以及壓力脈動的影響。
1 數學模型
計算流體力學(CFD)是流體力學的重要分支,在計算機科學發展下產生的介于數學、流體力學和計算機之間的交叉學科,主要研究內容是通過計算機和數值方法來求解流體力學的控制方程,對流體力學問題進行模擬和分析,主要遵循質量守恒、動量守恒和能量守恒三大定律,使用三大基礎方程對其進行描述,文章中未考慮溫度變化,因此不考慮能量守恒方程,剩余兩項的表述如下:
1)連續性方程
連續性方程是質量守恒定律在流體力學中具體表達,對流體采用連續介質模型,密度和速度在時間以及空間上都是連續、可微函數,數學表達式如下:
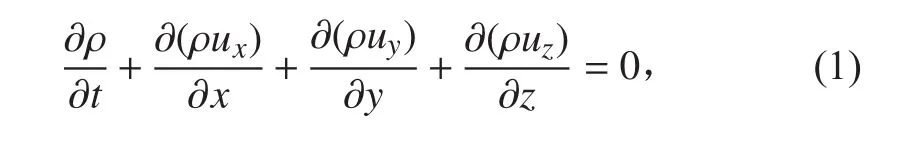
2)運動方程
運動方程是牛頓第二定律即動量守恒定律在流體力學中的具體表達,假設流體不可壓縮時,數學表達式如下:
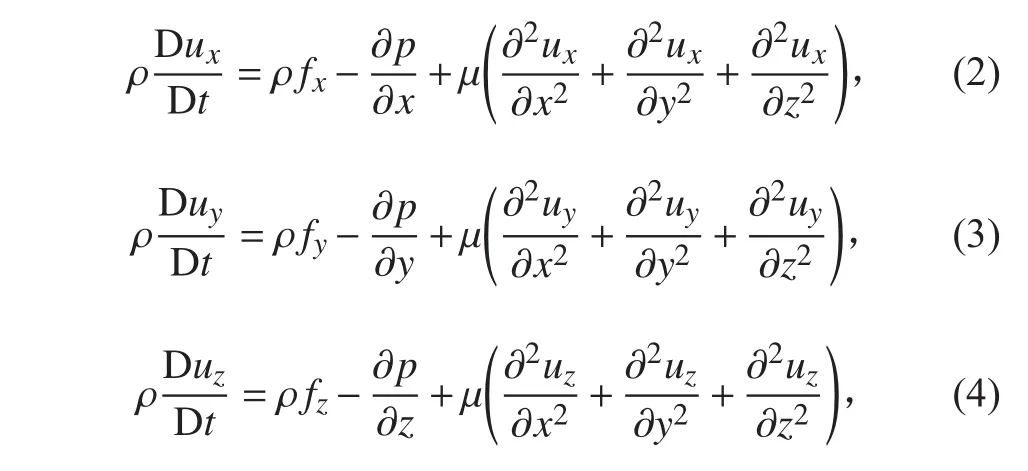
本文計算主要采用SSTk-ω,集成k-ε與k-ω兩種模型的優勢,近壁面處使用k-ω模型,邊界層使用kε模型,考慮湍流剪應力的輸運效應,對有壓力梯度引起的分離現象模擬更加精確,數學表達式如下:
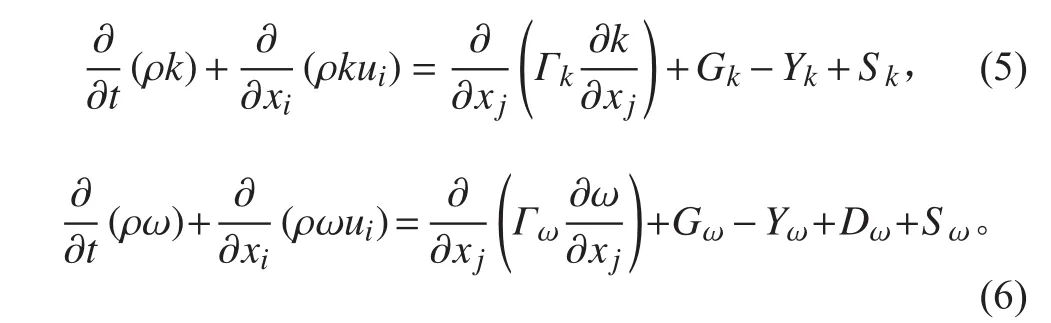
式中:Gk為層流速度梯度產生的湍流動能;Gω由ω方程產生;Γk和Γω是k和ω的擴散率;Yk和Yω由擴散產生的湍流;Dω為正交發散項。
2 計算模型
2.1 計算域及邊界條件選擇
計算域大小的選擇至關重要,從理論上來說計算域越接近真實流場其計算結果越真實,但是對于CFD計算來說,計算資源也是需要考慮的因素,受限于電腦的運行速度,計算域越小計算越快,因此需要在保證計算結果的前提下選擇較小的計算域。參考時忠民等[7]對繞流邊界影響的研究,取數值模擬計算域的進口距方柱取25B,上下兩側邊界距方柱取25B,出口距方柱取40B,其中方柱長為L,寬為B。計算域邊界左側為速度入口,右側為壓力出口,上下兩側為對稱邊界,方柱表面取為無滑移壁面,如圖1所示。
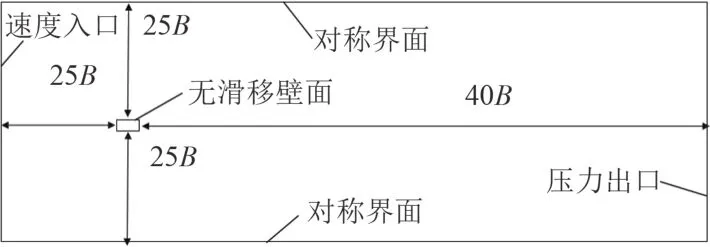
圖1 方柱繞流幾何模型示意圖Fig. 1 Geometric model diagram of flow around rectangular cylinder
2.2 網格獨立性及數值方法驗證
在數值模擬計算中,首先要驗證網格獨立性。網格劃分是前期最重要的工作且耗費時間長,網格的疏密及質量直接影響著計算規模的大小和計算結果的精確程度。通常認為當網格密度達到一定程度后,繼續增加網格量對于計算結果的影響非常小,此時可以認為網格疏密對于計算結果的影響可以忽略。網格劃分方式時均采用結構化網格,質量均可保證在0.8以上,可忽略質量差異對結果的影響。圖2給出了本文驗證網格獨立性所采用4套網格。
圖2 不同密度網格示意圖Fig. 2 Different density grid diagram
對于非穩態計算,時間步長的選取也將影響數值模擬結果的準確性。采用庫朗數(CFL)來調節計算的穩定性與收斂性。CFL越大,收斂速度加快但穩定性逐漸降低。表1給出雷諾數Re=5 000時,不同網格和時間步長下方柱繞流的升力系數的均方根值Cl.rms,阻力系數的平均值Cd.mean,斯特勞哈爾數St及各結果間的相對誤差。

表1 不同網格和時間步長下方柱繞流計算結果Tab. 1 Calculation results of flow around square column with different grid and time step
從表1可以看出,網格密度和CFL的變化對平均阻力系數Cd.mean和斯特勞哈爾數St的影響較小,最大相對誤差僅為3.87%。升力系數的均方根Cl.rms在網格數量較低時計算結果偏小,當網格數量到達11萬以上后計算結果也趨于穩定。因此考慮到計算消耗,本文劃分網格時采用114 619網格數量的劃分方式,時間步長上CFL值設置為5。
針對所選用的網格以及時間步長,并與文獻進行對比,驗證數值方法的正確性,結果如表2所示。

表2 數值文獻結果對比Tab. 2 Comparison of numerical and literature results
2.3 監測點及多方柱位置布置
探究方柱后流場壓力脈動分布規律,在后方均布25個監測點,左上角為1號監測點,從左向右依次編號,具體情況如圖3所示。多方柱繞流時,模擬實船格柵布置情況,以5個單方柱并列,在保持截面長寬比L/B=2不變的情況下,改變兩方柱中心距離D的尺寸從而改變方柱間距比D/B,本文取D/B=(5,4,3,2),多方柱時監測點與單方柱相同,具體尺寸布置及網格情況如圖4和圖5所示。
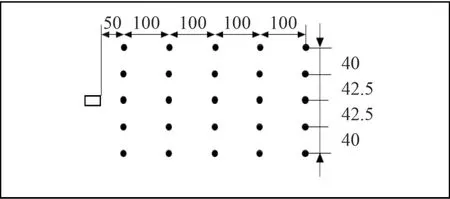
圖3 監測點分布示意圖Fig. 3 Distribution diagram of monitoring points
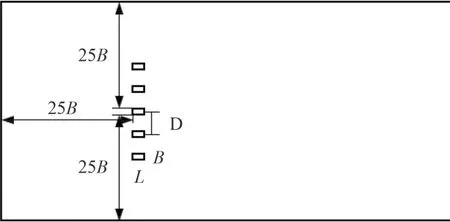
圖4 方柱位置布置示意圖Fig. 4 Schematic diagram of the position layout of the rectangular cylinder

圖5 網格示意圖Fig. 5 Grid diagram
3 結果分析
3.1 單方柱繞流分析
3.1.1 雷諾數影響分析
給定截面長寬比L/B為2,不同的雷諾數Re下繞流參數(升力系數的均方根值Cl.rms、阻力系數的平均值Cd、渦脫頻率F、斯特勞哈爾數St)如圖6所示,脈動壓力變化如圖7所示。
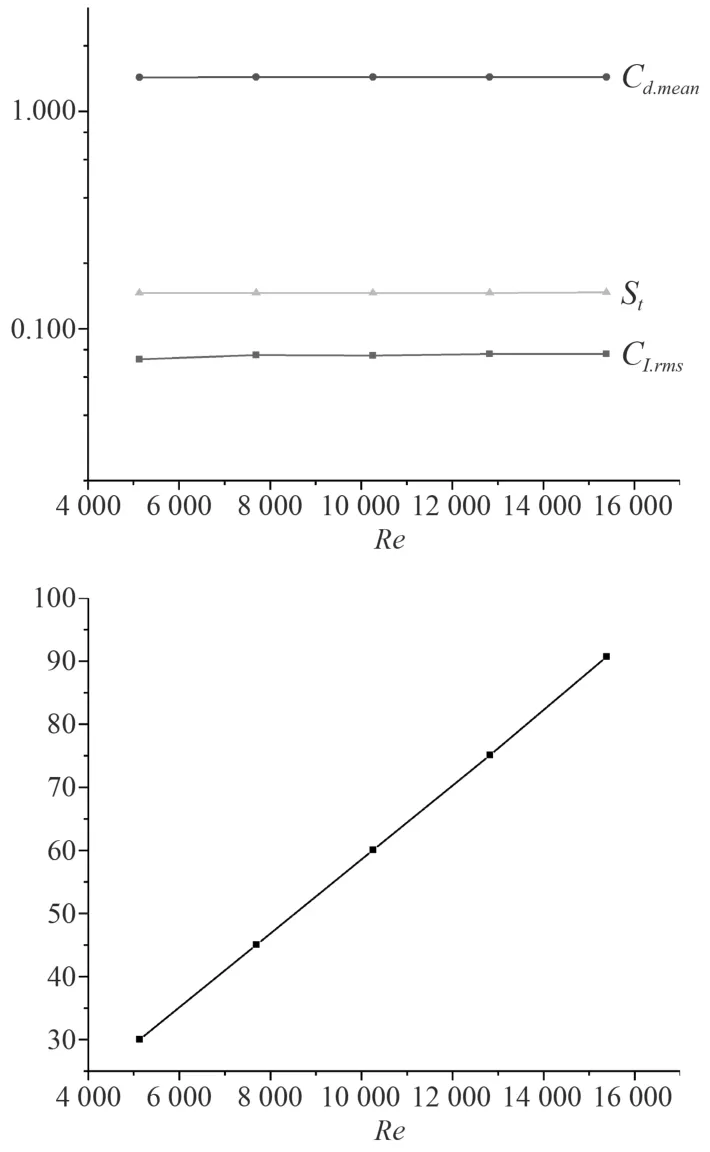
圖6 繞流系數變化曲線Fig. 6 Curve of variation of flow coefficient
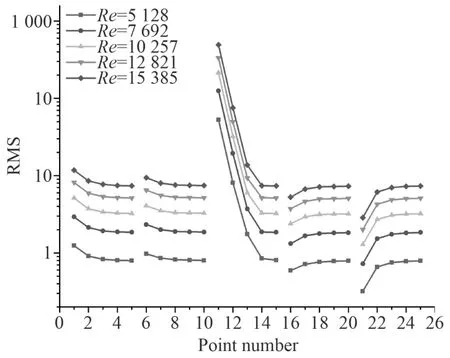
圖7 脈動均方根值曲線Fig. 7 Pulsating root-mean-square curve
如圖中所示,升力系數、阻力系數,斯特勞哈爾數變化很小,可以忽略不計,渦脫頻率隨雷諾數線性增加。各個監測點的脈動均方根值隨著雷諾數的增加而增加,總體來看,不同雷諾數下,壓力脈動均方根值變化趨勢趨于吻合。從監測點的位置來看,上面2行監測點均方根值遠離方柱呈現下降的趨勢,但變化幅度較小。位于流場中間的監測點壓力脈動均方根值遠離方柱也呈現下降趨勢,但變化劇烈。下方2行監測點壓力脈動均方根值隨距離增加而逐漸增大。
3.1.2 方柱截面長寬比影響分析
方柱截面的長寬比會對方柱后的流動產生顯著影響,本文分別取長寬比L/B為0.5,1,1.5,2,3的方柱進行數值模擬。各雷諾數下,不同長寬比時繞流參數如圖8所示。選取Re=15 385時,針對不同截面長寬比,各個監測點壓力脈動均方根值曲線如圖9所示。
由圖可知,不同雷諾數下,各繞流參數隨截面長寬比變化趨勢相同。當L/B=1,2時,阻力系數、升力系數以及斯特勞哈爾數重合較好;L/B=0.5,1.5,3時,阻力系數、升力系數以及斯特勞哈爾數在各自雷諾數下存在差異。阻力系數曲線與升力系數曲線先下降再上升,阻力系數曲線在L/B=1.5取得最小值,升力系數曲線在L/B=2.0時取得最小值。渦脫頻率曲線的變化規律與斯特勞哈爾數曲線相同,在監測范圍內先增大再減小,在L/B=1.5取得最小值時,逐漸增大。長寬比L/B=1.5,2時,壓力脈動均方根值明顯小于其他長寬比下結果,其中L/B=2時結果最小。長寬比L/B=0.5,1,3時,壓力脈動的均方根值較接近,交替出現最大值。
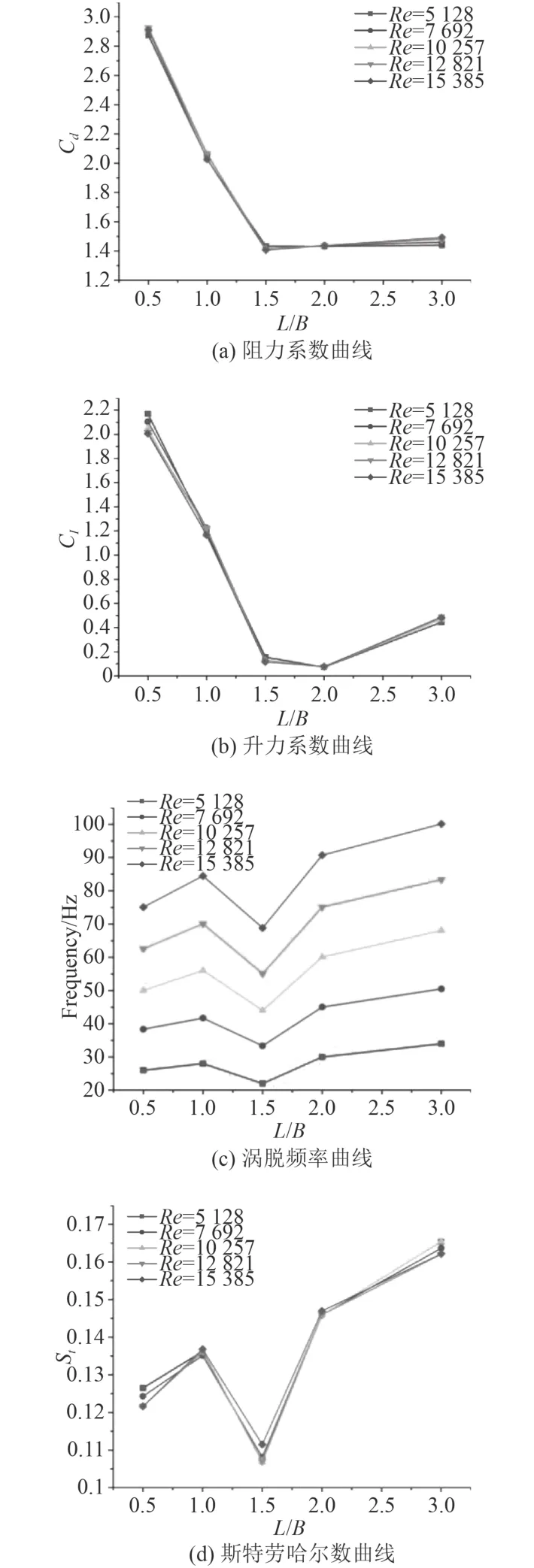
圖8 繞流系數變化曲線Fig. 8 Curve of variation of flow coefficient

圖9 脈動均方根值曲線Fig. 9 Pulsating root-mean-square curve
3.2 二維方柱群分析
3.2.1 雷諾數影響分析
方柱的間距比D/B=5,不同雷諾數下,方柱群繞流參數如圖10所示,方柱群后壓力脈動壓力如圖11所示。
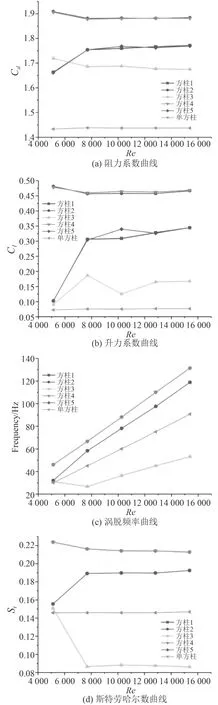
圖10 繞流系數變化曲線Fig. 10 Curve of variation of flow coefficient
從圖中可以看出,與單方柱相比,柱群的升力系數與阻力系數都有明顯的增加,其中位于中間位置的方柱3改變最小,中間兩側的方柱2與方柱4改變最大。方柱3的渦脫頻率與斯特勞哈爾數較單方柱有所下降,其余方柱明顯增加。從總體結果來看,對稱布置的方柱1與方柱5,方柱2與方柱4繞流參數變化趨勢與幅度接近一致。與單方柱相比,方柱群的壓力脈動均方根值均顯著變大,從均方根值變化趨勢看,除了中間一行監測點外,其余監測點變化趨勢與單方柱相同。
3.2.2 方柱間距影響分析
雷諾數為15 385時,不同間距比時方柱群繞流參數如圖12所示,不同方柱間距比下各監測點壓力脈動脈動壓力如圖13所示。
從圖中可以看出,繞流參數曲線(升力系數的均方根值Cl.rms,阻力系數的平均值Cd,渦脫頻率F、斯特勞哈爾數St)均具有很好的對稱性,方柱1和方柱5,方柱2和方柱4主要參數基本吻合。隨著間距比的增大,升力系數與阻力系數呈現減小的趨勢,方柱3變化最為劇烈。內部三方柱渦脫頻率隨間距比的增大而減小,但最外側兩方柱渦脫頻率隨間距比的增大而增大,當D/B=2,3時,中間方柱與其周圍方柱渦脫頻率差幅較小,隨著間距增大,呈明顯下降趨勢。斯特勞哈爾數曲線變化規律說渦脫頻率變化曲線大致相同。方柱間距比對流場壓力脈動的影響很明顯,位于流場前方的監測點壓力脈動隨間距比變化混亂,無規律可循。流場后方的監測點可以明顯發現,間距比D/B=2時壓力脈動的均方根值大于其它間距比結果。
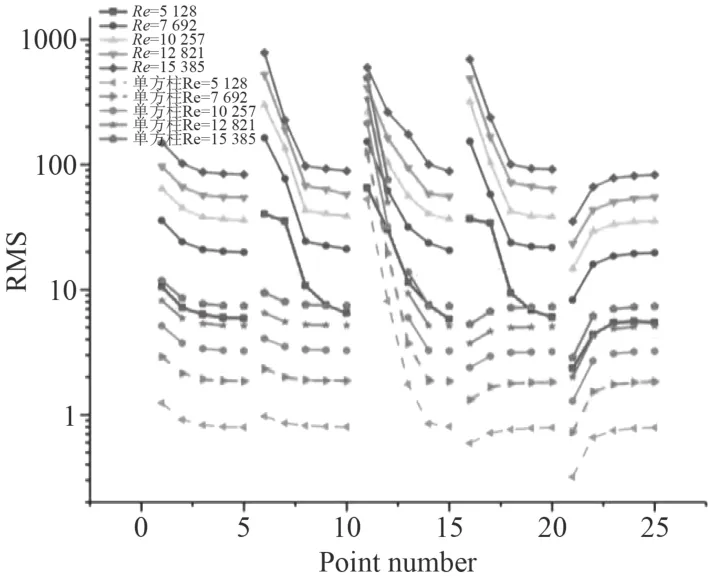
圖11 脈動均方根值曲線Fig. 11 Pulsating root-mean-square curve
4 結 語
本文分析了方柱的主要繞流參數和壓力脈動隨雷諾數以及方柱截面長寬比L/B的變化規律。在此基礎上,取定L/B=2,分析了雷諾數以及間距比對繞流參數以及壓力脈動的影響,現得出以下結論:
單個二維方柱下,雷諾數主要影響脈動壓力,各監測參數均隨截面長寬比發生較大改變;多方柱并列時,監測點參數較單方柱均有所提高,方柱間距比對脈動壓力影響較大。
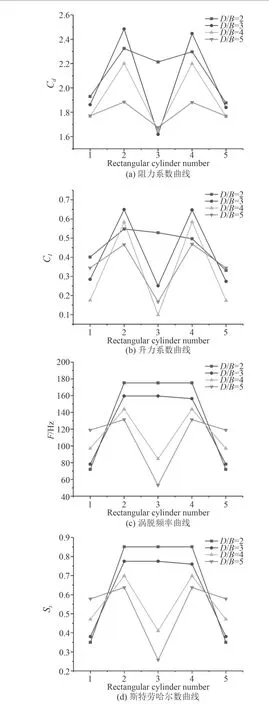
圖12 繞流系數變化曲線Fig. 12 Curve of variation of flow coefficient
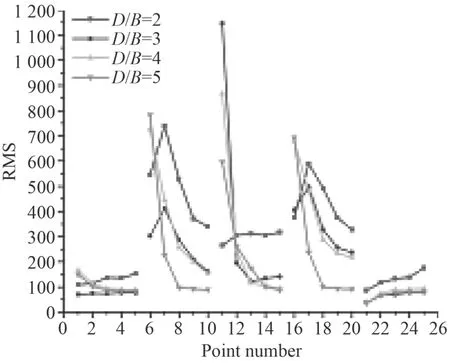
圖13 脈動均方根值曲線Fig. 13 Pulsating root-mean-square curve

