一種逆向平滑的純方位目標跟蹤初值優化方法

鄭 藝，王明洲

(中國船舶集團公司 第705研究所，陜西 西安 710077)

0 引 言

純方位目標跟蹤方法是在被動測量的情況下，根據傳感器測量到的受到噪聲污染的方位數據來估計目標運動特性的跟蹤方法，在許多領域有著非常廣泛的應用[1]，例如雷達、水下、航空等領域，特別是在水下環境中，這種跟蹤方法備受關注。尤其是本文將要討論的單站純方位目標跟蹤，它的優點在于可以僅通過單個觀測站在隱蔽狀態下對目標進行被動的觀測，并進行運動參數的估計，從而可以單獨秘密地進行行動策劃并對目標實施打擊。但由于單個觀測站所能獲得的觀測數據有限，系統可觀測性差，對目標的定位和跟蹤難度更大。因此，單站純方位目標跟蹤是水下目標攻擊領域中最受關注的一種方法，它既是目標跟蹤算法領域中的基本方法，又是公認的最具挑戰性的一大難題。隨著水下目標的運動速度不斷提高，對水下快速目標的跟蹤定位提出了新的挑戰。

單站純方位目標跟蹤方法的研究熱點集中在批處理和遞推類估計兩大類方法中。其中遞推類估計方法由于模型簡單、數據儲存量小的特點，更加適合計算機應用，已經成為目標定位跟蹤方法的發展方向和研究熱點[2]。由于水下單站純方位目標跟蹤模型是非線性的，線性濾波效果不佳，用于此方面的遞推類估計方法有：擴展卡爾曼濾波[3]、無跡卡爾曼濾波[4]、粒子濾波[5]等。

遞推類估計方法有一共同難點在于，由于遞推的性質，后一時刻的結果依賴于前一時刻，誤差易隨迭代過程擴大。對于卡爾曼系的算法，還有一大問題在于估計結果對于估計初值的選取十分依賴，起始時刻誤差通過迭代始終影響后續時刻的濾波，因此起始時刻初值的準確度對后續的參數估計和目標跟蹤的效果有著較大影響。近年來一些文獻研究了雙向濾波[6-8]或者是后向平滑[9-11]的濾波方法，試圖通過正反向的濾波，增加對觀測數據的利用，以提高估計精度。但這些方法都是針對濾波中上一時刻的優化，沒有對濾波初值進行單獨優化，對于短時觀測的情況，誤差降低效果有限。本文的研究是在這種后向濾波思路的基礎上，采用一種逆向平滑方法對濾波的初值進行優化，使整個跟蹤過程的誤差降低，提高短時觀測下快速目標跟蹤的準確度。

1 單站純方位目標運動模型

只考慮目標在二維平面運動，假定目標做勻速直線運動，坐標系如圖1所示。X軸指向正東，Y軸指向正北，觀測站初始位置位于坐標原點，目標在XOY平面運動。為目標初始距離，為目標運動航向，為目標的運動速度，時刻對應的目標方位，是時刻觀測平臺位置對應的坐標，是時刻對應的目標與觀測平臺之間的距離。顯然，對于勻速直線運動的目標，能夠唯一地確定目標的運動軌跡。

對于勻速直線運動的目標，系統的狀態空間模型可表示為：

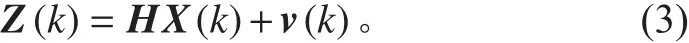
當觀測量是方位角時，觀測方程可以寫為：

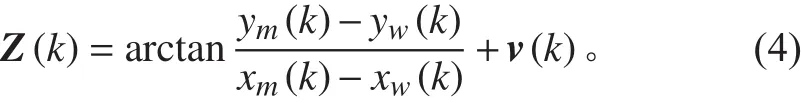
2 卡爾曼估計算法系

觀測方程（4）是非線性的，而卡爾曼濾波算法是線性的，應用于純方位目標運動分析，通常是將其進行各種方式的處理改進，形成非線性濾波方法。但其實這類算法的核心部分是類似的，以傳統的卡爾曼濾波算法為例，說明其原理。

卡爾曼系濾波算法通常首先根據式（2）和式（3）構造遞推卡爾曼濾波器，過程如下：

1）狀態一步預測

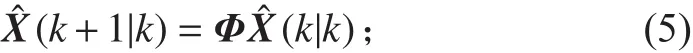
2）狀態更新

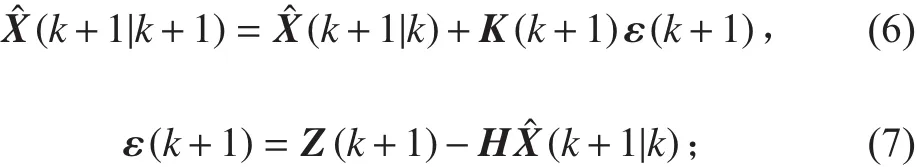
3）濾波增益矩陣

4）一步預測協方差

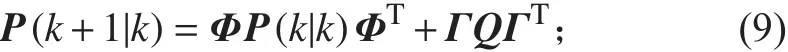
5）協方差陣更新

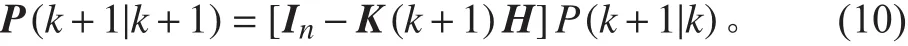
3 基于逆向平滑的初值優化

由于卡爾曼濾波算法的遞推性質，導致其對濾波初值的選取十分敏感，后段濾波依賴于前段濾波的結果，因此初值誤差的影響長時間地存在于濾波過程中。本文提出一種初值的優化方法，通過卡爾曼濾波的逆向遞推，對濾波初值進行重新估計，降低初始的估計誤差，從而提高整個濾波過程的精度。

3.1 逆向平滑

式（5）～式（10）描述了一般的正向卡爾曼濾波類方法的基本過程，作為遞推類的濾波，這一過程是可以進行逆向遞推的，其原理如下：

將式（2）展開，有

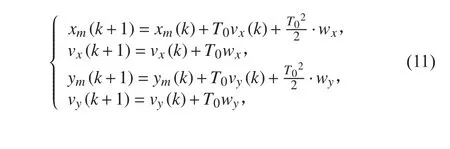
對于勻速直線運動目標，可以認為目標速度不變，即

將式（11）中等號左右移動，并將式（12）代入整理得：

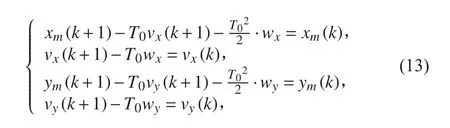
可將方程組（13）用矩陣表示為：

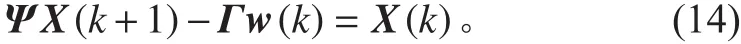
其中：

將式（14）與式（3）組合，可構造出一組新的狀態空間模型。此空間模型同樣適用于卡爾曼濾波方法，將這組新的狀態空間模型運用到卡爾曼濾波的遞推過程中，可以實現從時刻向時刻逆向遞推，過程如下：

1）狀態一步逆向預測

2）狀態逆向更新

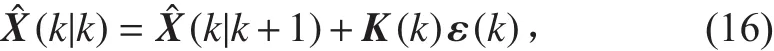
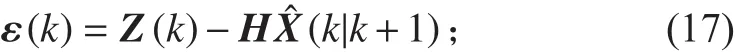
3）濾波增益矩陣

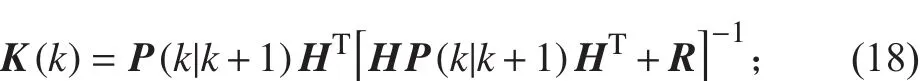
4）一步逆向預測協方差

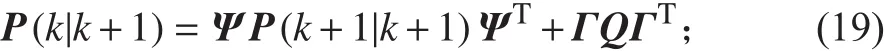
5）協方差陣逆向更新

由于這種逆向平滑的估計值是通過正向的卡爾曼濾波得到的估計值再次經過逆向卡爾曼濾波得到的，增加了觀測數據的正反向運用，減少了估計的誤差。

3.2 初值優化

取十分敏感的問題，將上述逆向平滑濾波運用到對初值的優化中，步驟如下：

對于無跡卡爾曼濾波、擴展卡爾曼濾波及各種改進的卡爾曼濾波方法而言，雖然各方法的具體步驟不同，但由于各種算法的核心部分都是基于卡爾曼濾波的，因此上述初值優化過程也同樣適用于其他的卡爾曼系的濾波方法。

4 仿真試驗

為了驗證所提出的基于逆向平滑的初值優化方法對純方位目標跟蹤軌跡的改善性能，選用無跡卡爾曼濾波和擴展卡爾曼濾波兩大經典的卡爾曼系濾波方法進行試驗，分別用2種方法進行基于逆向平滑的初值優化，驗證使用所提方法優化初值后對整個跟蹤結果的改善效果。

4.1 仿真條件

根據快速目標短時跟蹤的背景需要，設置目標和觀測站運動軌跡如下：目標做勻速直線運動，初始位置坐標為（100 m，-400 m）；目標運動速度為50 kn，航向為-41°，即直角坐標系下目標的初始速度為（-30，40）kn，換算單位后為（-15.42，20.56）m/s，目標真實的狀態向量為（100，-15.42，-400，20.56）。觀測站的初始位置（0 m，0 m），以45 kn的速度向-36°方向勻速直線運動50 s，而后向-63°方向繼續以45 kn速度勻速直線運動100 s。針對目標運動速度快、觀測時間較短的問題，設置觀測站方位估計頻率為10 Hz。設置各項誤差條件如下：

1）仿真條件1

觀測站方位估計誤差的標準差為2°，初始距離估計誤差為10%，初始速度矢量估計誤差為10%。設置此仿真條件為基礎仿真條件，其他仿真條件在此基礎上對比。

2）仿真條件2

在條件1的基礎上，增加目標方位估計誤差的標準差為8°，其他條件不變。

3）仿真條件3

在條件1的基礎上，增加初始距離估計誤差為20%，其他條件不變。

4）仿真條件4

在條件1的基礎上，增加初始速度矢量估計誤差為20%，其他條件不變。

4.2 無跡卡爾曼仿真結果對比

在仿真條件1下，分別采用無跡卡爾曼濾波和基于逆向平滑的初值優化的無跡卡爾曼濾波2種方法，進行200次蒙特卡羅試驗，并將200次仿真試驗中2種方法的誤差進行平均，結果如圖2所示。

在圖2給出的仿真結果中，進行50個采樣點的逆向遞推，即步數的取值為50。圖2（a）為位置坐標的估計值與位置坐標真實值之間誤差，2條曲線分別為無跡卡爾曼濾波初值優化前后的誤差比較；圖2（b）為優化前后速度標量估計值與真實值之間的誤差比較；圖2（c）展示的是目標航向的估計值與真實目標航向間的誤差，在初值優化前后的比較；圖2（d）為目標距離估計值與真實值間的誤差在初值優化前后的比較。可以看出，對于無跡卡爾曼濾波，經過初值優化后，各項誤差均有明顯降低，并且這種誤差的縮小在整個150 s的觀測與估計過程中都存在，尤其對于誤差峰值的降低效果明顯。在對目標各項參數估計中，經過初值優化的方法比普通的無跡卡爾曼濾波對誤差峰值處的降低更為明顯，這樣可以縮小誤差的范圍。

為了對比不同仿真條件下初值優化方法的效果，分別在條件1、條件2、條件3、條件4下進行仿真試驗，取200次蒙特卡羅試驗的誤差進行平均，并將優化前后的平均誤差統計如表1所示。

對于分別增大方位估計角度誤差標準差、增大初始速度估計誤差、增大初始距離估計誤差后，本文所提方法對無跡卡爾曼濾波的誤差降低依然有效，但誤差降低率有所下降。

4.3 擴展卡爾曼仿真結果對比

用擴展卡爾曼濾波對比本文所提基于逆向平滑的初值優化的擴展卡爾曼濾波，在給出的仿真條件下分別進行200次蒙特卡羅試驗，并將200次仿真結果中2種方法的誤差進行平均處理，結果如圖3所示。

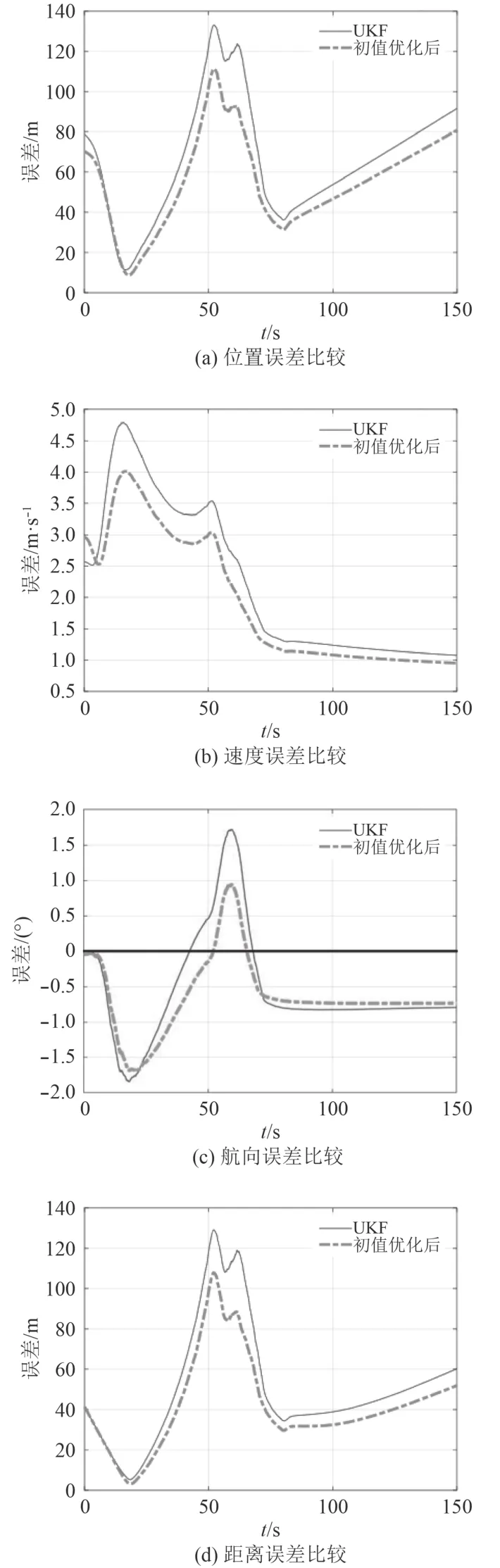
圖2 無跡卡爾曼濾波仿真結果Fig. 2 Simulation results of Unscented Kalman filter

分別根據條件1、條件2、條件3、條件4這4組仿真條件進行200次蒙特卡羅試驗，統計擴展卡爾曼濾波初值優化前后平均誤差，對比結果如表2所示。

由表2可知，在增加方位估計誤差標準差、初始速度誤差、初始距離誤差后，本文所提初值優化方法對擴展卡爾曼濾波的誤差降低率下降，但依然有降低誤差的效果。

綜合表1與表2的結果，本文所提逆向平滑初值優化方法對于無跡卡爾曼濾波和擴展卡爾曼濾波有著相似的效果。對比不同仿真條件下的誤差降低率，此優化方法在條件1下有著更高的誤差降低率，說明此方法在各項初始誤差和方位誤差標準差更低、環境條件較好時有更明顯的優勢。

表1 無跡卡爾曼濾波優化前后平均誤差Tab. 1 Mean error before and after UKF optimization

4.4 逆向濾波步數的影響

對于本文所提的對初值的逆向濾波優化，有一個重要的影響因素即為逆向步數的取值。為了探究所提初值優化方法中逆向濾波步數對誤差的影響，在仿真條件1下分別基于無跡卡爾曼濾波和擴展卡爾曼濾波，采用不同步數的逆向濾波對初值進行優化。每種不同的逆向步數優化下，分別進行200次蒙特卡羅試驗，每次對目標進行150 s的觀測和跟蹤，并將150 s內的估計誤差求均值。表3為無跡卡爾曼濾波下初值優化前后誤差比較，表4為擴展卡爾曼濾波下初值優化前后誤差比較。

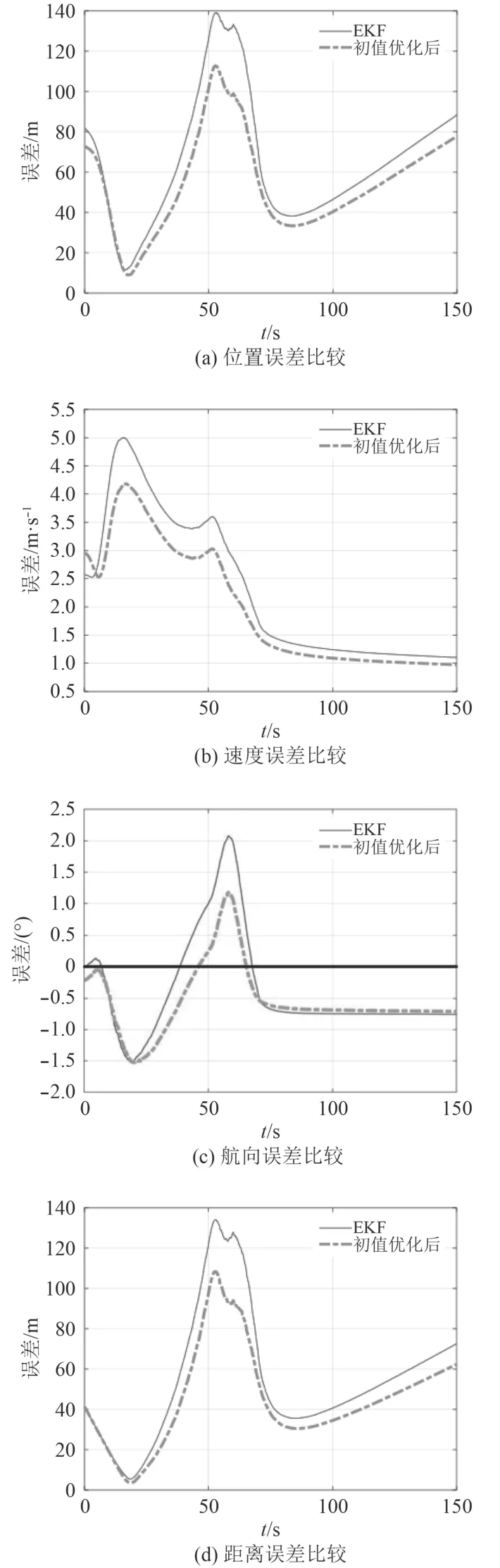
圖3 擴展卡爾曼濾波仿真結果Fig. 3 Simulation results of extended Kalman filter

根據表中數據可以看出，在逆向濾波步數不超過400的時候，經過逆向濾波初值優化的結果具有更低的濾波誤差，而逆向濾波步數在450點以上時，未經初值優化的傳統濾波方法具有更低的濾波誤差。對比不同的運動參數估計，逆向濾波的初值優化對于目標速度和目標距離的估計更加準確，而對于目標航向估計的性能提升相對不明顯。對于UKF和EKF，均是在逆向濾波步數為150的時候取得最佳的優化效果，此時對位置坐標估計誤差的平均降低率分別達到了65.90%和65.38%。

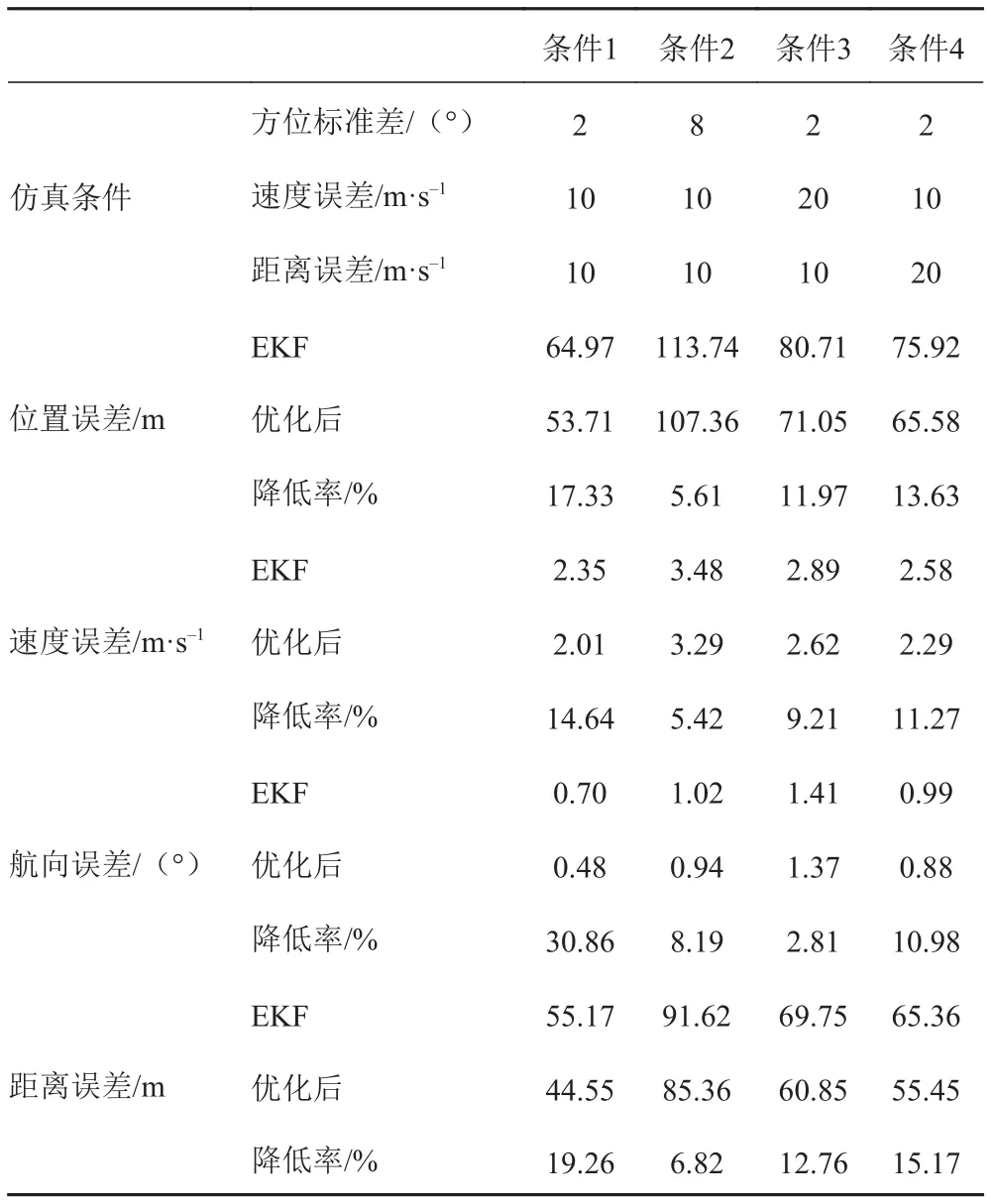
表2 擴展卡爾曼濾波優化前后平均誤差Tab. 2 Mean error before and after EKF optimization

以目標位置坐標的估計為研究對象，比較本文所提的逆向濾波初值優化方法對于UKF和EKF的優化效果，統計不同逆向濾波步數對位置估計誤差的影響，結果分別如圖4和圖5所示。

從圖4和圖5可以看出，通過改變逆向濾波步數，不論是UKF還是EKF，逆向濾波步數對于優化效果的影響是非線性的。并不是逆向濾波的步數越多優化效果越好，對2種濾波的優化均在逆向濾波步數取值150的時候取得最低的目標位置估計誤差，在此之后，隨著逆向濾波步數增加估計誤差增大，在逆向濾波步數到400點以上，優化后的誤差甚至超過原本UKF或EKF的誤差，失去了優化的意義。當逆向濾波步數在150點左右時可取得最佳的優化效果，對誤差的降低率達到最高。其原因在于在該仿真條件下150點左右正向濾波即觀測15 s時估計誤差較小，此時估計正向濾波誤差取得局部極小值。根據圖2（a）和圖3（a）所顯示的目標位置估計誤差，不論對于EKF還是UKF，在觀測時刻15 s左右即150點左右時刻，目標位置坐標估計的誤差取得極小值，利用此時時段內較小誤差的估計值進行逆向濾波，理論上可取得更小的誤差，得到初值優化的效果更佳。而濾波誤差的極小值點的取得步數或者是濾波收斂的步數是不一定的，它與目標和觀測站的運動軌跡有關，因此在不同的場景下的最佳逆向濾波步數是不同的，不具有普適性。

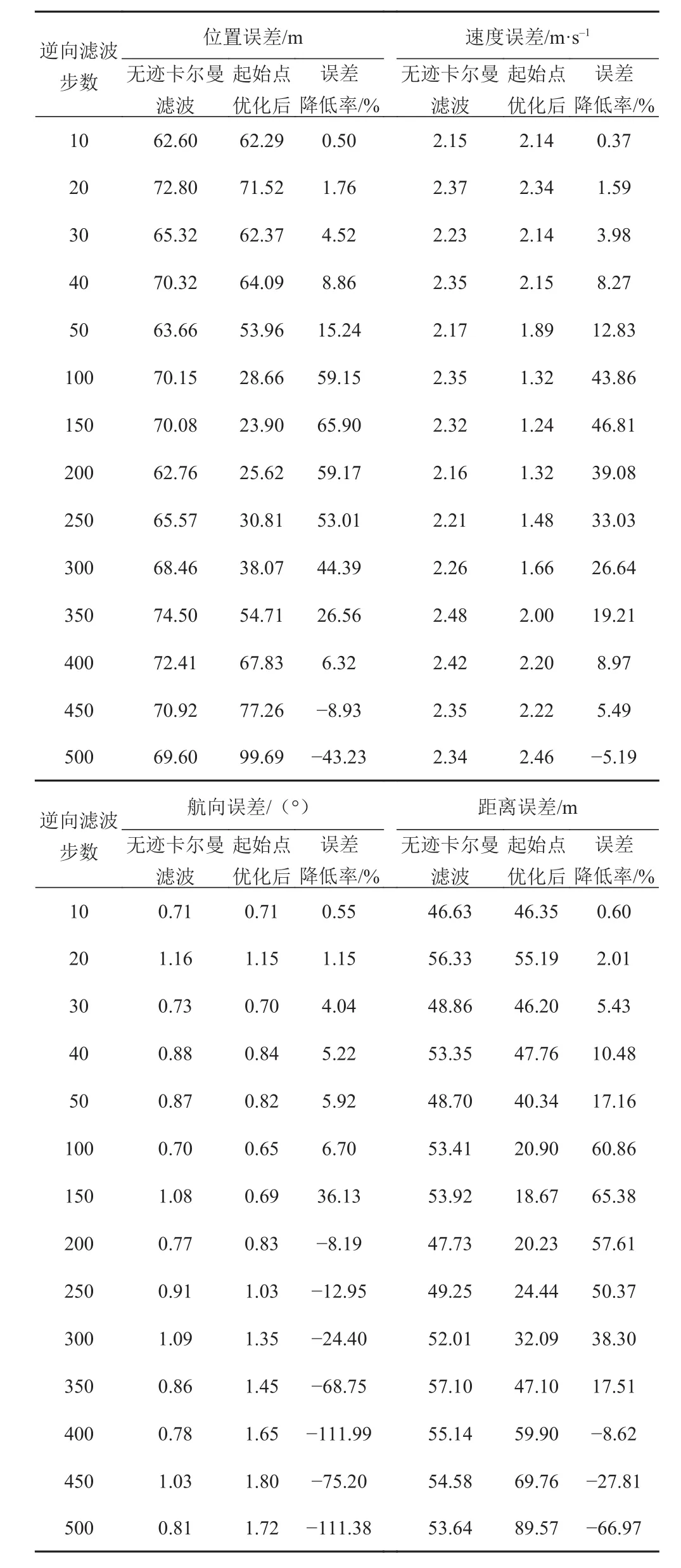
表3 不同逆向步數無跡卡爾曼濾波優化前后誤差比較Tab. 3 Error comparison before and after optimization of different reverse steps of Unscented Kalman filter

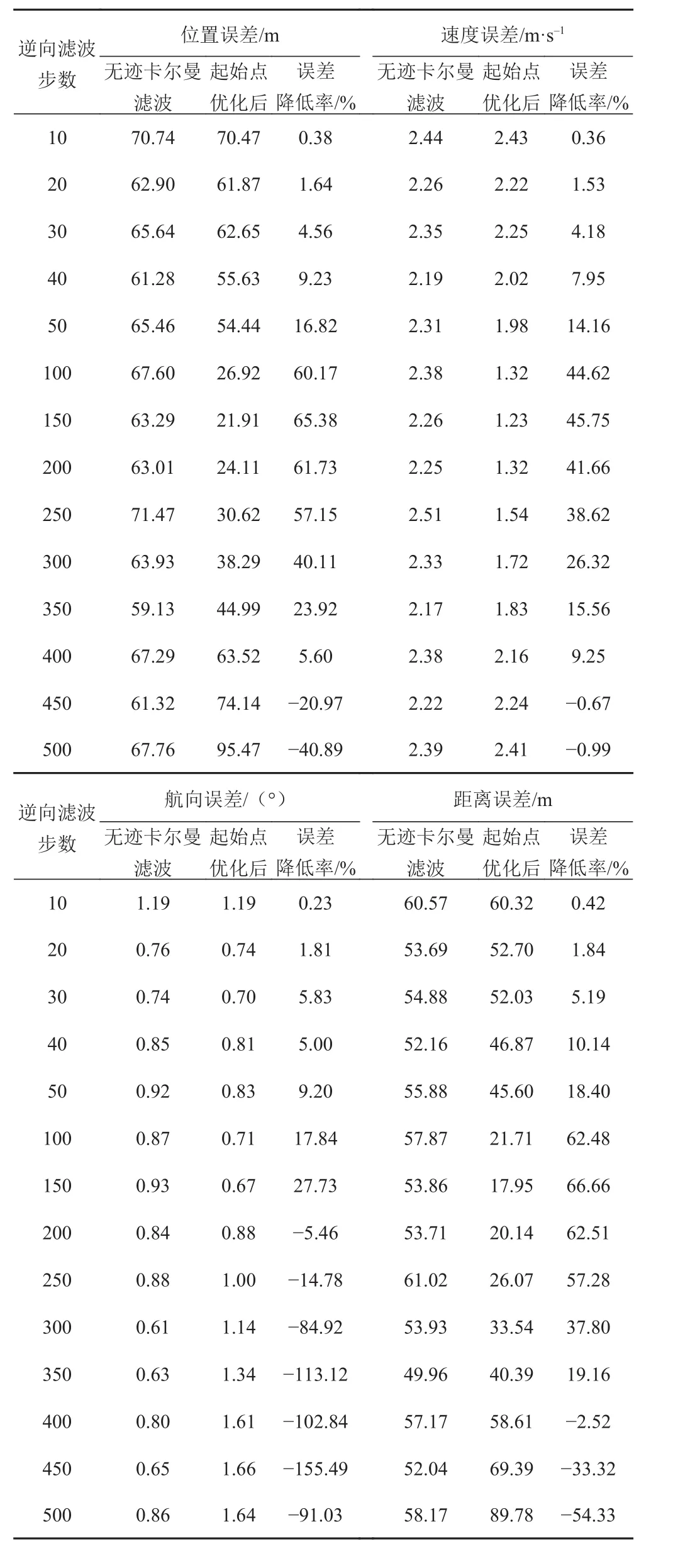
表4 不同逆向步數擴展卡爾曼濾波優化前后誤差比較Tab. 4 Error comparison before and after optimization of different reverse steps of Extended Kalman filter

但這并不意味著逆向濾波步數在濾波誤差最低時是最佳選擇，由于逆向濾波需要取得一定量的觀測數據作為先驗，更多步數的逆向濾波需要更多的觀測數據和觀測時長，同時需要更大的計算量。

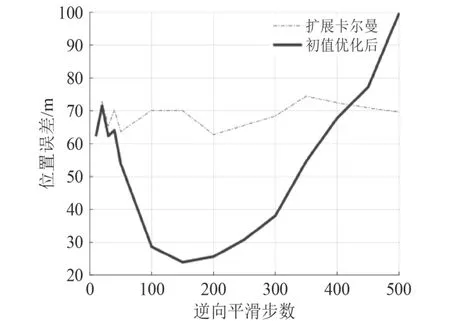
圖4 步數對優化后UKF的影響Fig. 4 The influence of the number of steps on the optimized UKF

圖5 步數對優化后EKF的影響Fig. 5 The influence of the number of steps on the optimized EKF

5 結 語

本文研究背景是基于快速目標短時觀測下的目標跟蹤，根據仿真結果與比較分析可得，本文所提基于逆向平滑濾波的初值優化方法對于無跡卡爾曼濾波和擴展卡爾曼濾波都有效果，對于目標位置坐標估計誤差、目標速度估計誤差和目標距離估計誤差都有明顯的縮小，并且在分別增大方位估計誤差標準差、距離初值誤差、速度初值誤差后，本文所提方法依然有效縮小估計誤差。本文所提方法雖然只改變濾波的初值，但在目標跟蹤中對于誤差的縮小有著長時間的效應。優化的效果和算法的實時性均與逆向平滑的步數有關，在實際應用中，可根據需求選取適合的逆向平滑步數，以滿足不同的實際需求。