雷達最大探測范圍可視化

王欣，趙兀君，李輝

（1.四川大學計算機學院，成都 610065；2.海軍裝備部，南昌 333000）

0 引言

電磁活動在人們的生活中隨處可見又是“不可見”的。在軍事方面，數量巨大、功能各異且分工明確的電磁設備扮演著重要角色，堅守在自己的“崗位”上。雷達用于戰場信息的探測、是武器系統的重要組成部分，它是重要的傳感裝置，能夠檢測到遠距離外的超出人們視力范圍的事物，并且通過數據反映出來。但是這些數據相對來說還是比較抽象，難以讓人在第一時間把握總體態勢，而對空間中的電磁環境準確認識又恰恰是決策的根本條件之一。那么將抽象的數據或是二維的圖形進行三維的顯示，能夠更加直觀，對于理解當前的情況更加友好。

關于雷達探測范圍的問題自有雷達以來就一直在被人們所討論，也是衡量雷達性能的重要指標。自由空間下的計算有Kerr 提出的距離公式，利用信噪比等因子進行理想化的計算。評估電波傳播特性有拋物方程法，可以分析地表起伏、電磁特性變化及大氣折射率變化等條件下的電波傳播問題[1]。對于雷達的各種衰減因素也有很多方法進行分析，例如對于大氣影響，可以用等效地球半徑方法仍然將電磁波傳播路徑作為直線來處理有關大氣折射的問題；氧氣和水蒸氣吸收衰減方面有Libebe 和ITU-R 模型，以及利用雙線性內插法計算水平-垂直非均勻大氣折射剖面等[1]。對于雷達探測概率的計算有Marcum 和Swerling 模型和概率融合公式。

1 雷達探測范圍

雷達是一種用于探測和定位反射目標的電磁傳感器。雷達誕生初期多是為軍事需要提供服務，可以監視海陸空、完成偵查任務、實現精準打擊、導航等。今天軍隊仍然是雷達的主要用戶和雷達技術的主要開發者[2]。

雷達通過發射電磁波并接收目標物體反射回來的電磁波后對信號進行的解析處理來得到有關目標的信息。雷達結構可以概括為發射機、天線（如果是單基地雷達只有一根天線）、回波接收機、信號處理機以及顯示器這幾個主要部分。對于不同的功能需求和應用目的可能還有抗干擾等輔助設備。

1.1 雷達距離方程

（1）雷達探測范圍概述

①雷達距離方程

雷達距離方程包含了許多關于雷達系統的以及雷達所處環境的參數。下列方程是由Kerr 提出，在自由空間下成立的雷達公式（我們這里表示的自由空間指的是除了雷達以及目標外，以雷達為中心并延伸到遠遠超出目標范圍以外的球形區域是空的，是一種理想條件）：

其中的參數表示為：

Pr 表示（天線終端處）接收信號功率，Pt 表示（天線終端處）發射信號功率，Gt 表示發射天線功率增益，Gr表示接收天線功率增益，σ表示雷達目標截面積，λ表示波長，Ft 表示發射天線到目標路徑的模式傳播因子，Fr 表示接收天線到目標路徑的模式傳播因子，R 表示雷達到目標之間的距[3]。方程中的Ft 表示的是目標處的實際電場值和自由空間理想條件下距雷達相同距離處沿著天線波束的最大增益方向的電場強度E0 的比值，包含天線方向圖因子以及各種影響因素（如大氣、地形等）。這里的方程針對單基站雷達，雷達的發射天線和接收天線相同，因此與之相關的參數中Gt、Gr 相等，Ft、Fr 相等，方程可以寫成下列形式：

變換方程，可知如果可以得到Pr的最小值，也就是Prmin，我們能夠計算出最大的距離值Rmax。

根據資料知，Pr與Pt的比值與信噪比相關。

信噪比的值為設備或系統接收并處理的來自外部的信號與接收設備產生的噪聲信號的比值。

在這里（雷達系統中）信噪比可以表示為：

Pn表示的是接收機噪聲功率的電平。Pn與接收系統的噪聲溫度Ts相關：

這里的k 是Boltzmann 常數，Bn表示接收機預檢測濾波器的噪聲帶寬，Ts以開爾文為單位，一般取值為290K。由此可得：

引入系統總損耗L，最后的最大距離公式如下：

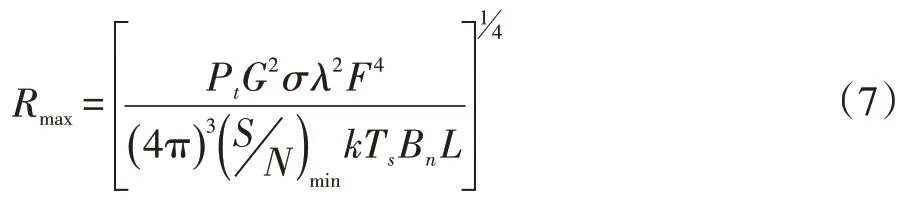
②雷達方向圖因子

天線具有方向性。通過在空間坐標上的電場強度與空間方向的三維關系圖可以描述天線的方向性。根據不同的方向圖特點，我們可以把雷達分為全向雷達，高斯型雷達，SIN（X）∕X 型雷達等。不同輻射水平下的最大天線輻射強度，可以用方向圖因子來描述。

對于高斯型雷達，它的方向圖函數為：

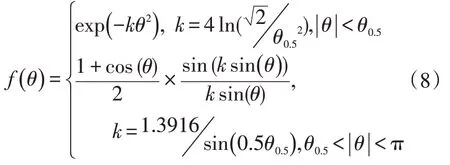
其中的θ表示目標在垂直方向上偏離雷達天線主軸的角度，θ0.5表示雷達主瓣寬度[4]。

對于 SIN（X）∕X 型雷達，它的天線方向圖函數為[4]：

其中ΔA=θ-Aelev，這里的Aelev指的是雷達天線仰角這里的bw 與前文的θ都指的是雷0.5達波束寬度（beamwidth）。Amax是雷達主瓣的最大角度，

（2）雷達探測范圍模型

建模時，我們使用結構體保存雷達系統的相關參數。之后將空間分層，每個水平層根據設定的步長和步數計算頂點坐標，其排布為圓形。同時在垂直方向，也通過設定步長和步數，計算完一個水平層后進行下一個水平層頂點的計算。這里我們需要根據一定的順序排布頂點，使之有一定的規則性，組合成面元，形成整個包絡面。在使用三角形面元（Triangle_strip）的情況下，需要交錯求出上下兩層頂點。構造包絡的流程如下：

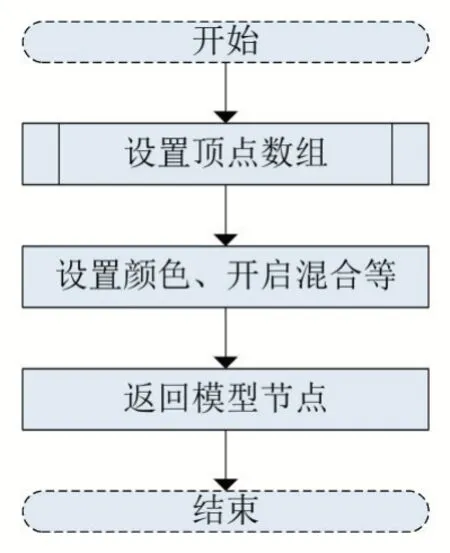
圖1 總流程

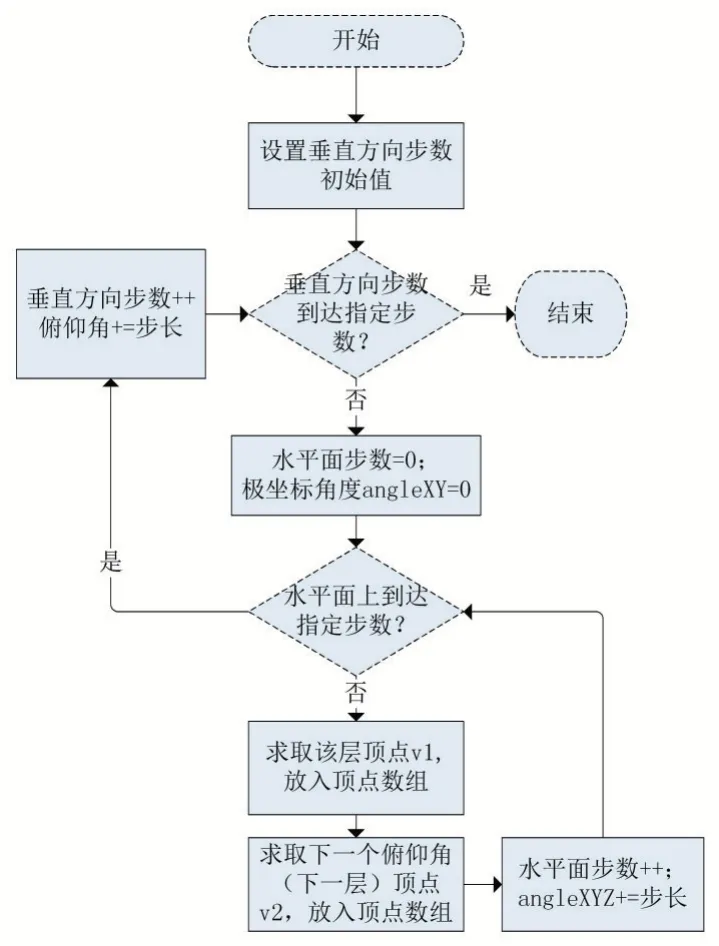
圖2 生成頂點流程

自由空間下，實際上每一層的包絡相當于一個給定半徑的圓，這種情況下使用極坐標來表示后可以很容易生成在世界空間下的坐標，當在地球上顯示時則要轉換為地球經緯度表示。

1.2 雷達探測概率

（1）雷達探測概率理論

雷達信號的檢測并不能達到完全準確，可能會由于接收電路中的噪聲電壓產生一定的誤差。將信號出現時被探測到的幾率定義為Pd，將Pfa定義為接收系統產生的噪聲波動被誤認為是信號的概率，也即虛警概率。

對于雷達探測概率的計算有多種計算模型可以使用。主要有兩種，一是針對穩定目標的Marcum 模型，一是針對起伏目標的Swerling 計算模型。

Marcum 模型[7]：

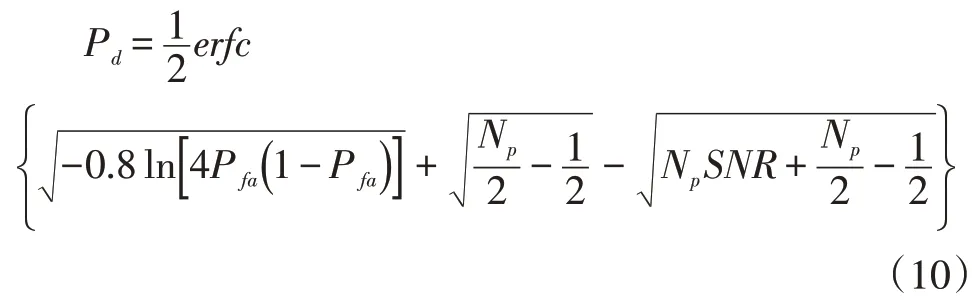
我們可以根據其函數圖像得知：

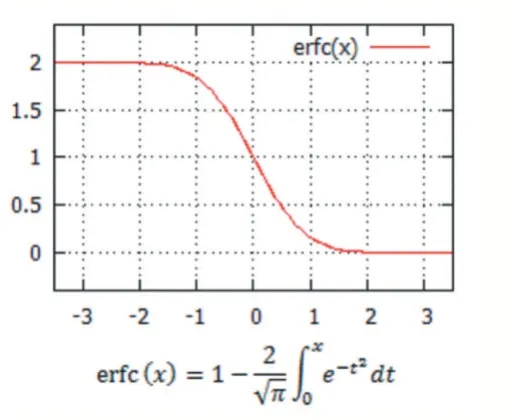
圖3 余誤差函數曲線圖

當x 小于-2 時的值是確定的，概率會恒等于1。也即對于Marcum 概率公式，只有當 x，滿足一定的條件時，求出的概率值才是有效的，由于虛警概率這里相當于常數，因此當累計脈沖數Np 達到一定值時，才能求出較為正確的概率值。

（2）雷達探測概率可視化

自由空間下，在忽略地形遮擋的情況下（若遮擋時，探測概率為0），同樣將空間分層，但是在每一個水平方向上，我們只需要根據一個軸（例如X 軸）的方向來設定步距求每一點的概率值。每一點的概率都不相同，我們這里構造概率為0.5、0.7、0.9 的包絡面。

求出滿足條件的坐標后我們獲得它距雷達的距離以及俯仰角，構造出該水平層上所有的坐標，再求出垂直面上所有層的坐標，每一層的坐標數量相等，可以采用四邊形面元，逆時針分別將原數組中的點以及右邊，右上，正上方的點加入最終的頂點數組中用于構造包絡。

求滿足條件的坐標流程如圖4。

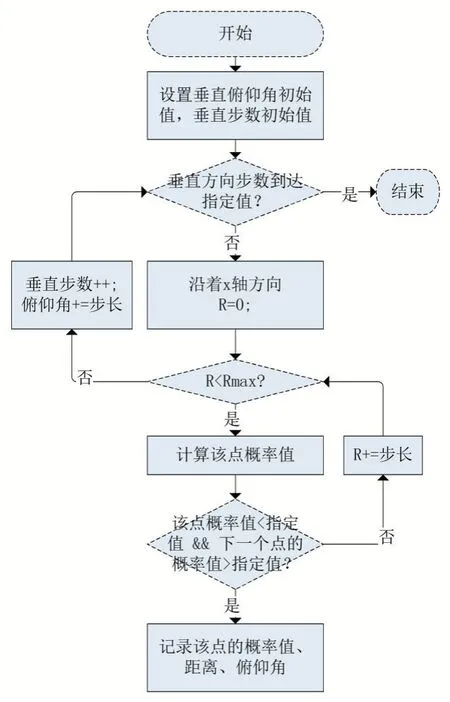
圖4

計算概率的過程中根據Marcum 公式我們需要先進行信噪比的計算，然后進行概率值的計算。由于最小信噪比是我們給出的，且根據最大距離公式反推我們可以得到：

可以推出：

構造最終頂點坐標的流程如圖5。

1.3 影響雷達探測范圍的因素

（1）干擾機干擾

作戰時或遇到其他情況時，雷達不僅會接收到它本身發出的電磁波，還可能收到自然界產生的或干擾機發出的干擾信號。當有多個干擾機存在時，目標雷達接受信號功率需要進行修改，干擾信號功率進行累加就可以得到目標雷達能夠接收到的總干擾信號的值：

此時關于雷達信噪比的計算要將分母加上接收到的干擾機的信號功率，調整為：

（2）地形因素

崎嶇的地形、山坡山峰等會阻礙電磁波的傳播。因此我們需要通過雷達位置到邊界點的連線是否受到地形阻擋來重新定義邊界點。

其思路是：與自由空間下雷達最大探測范圍模型求取頂點的步驟相同，但是要根據地形對頂點位置進行調整。從雷達所在的坐標處向該方向發射一條射線，射線的長度以100 米為單位遞增，計算該射線到達處的坐標值以及高程值，如果該處的地形高度值大于該處頂點的高度，說明遇到阻擋，將該點記錄下來，如果沒有遇到阻擋且不超過邊界范圍，將邊界點記錄。

根據地形因素重新規劃頂點的流程如圖6。

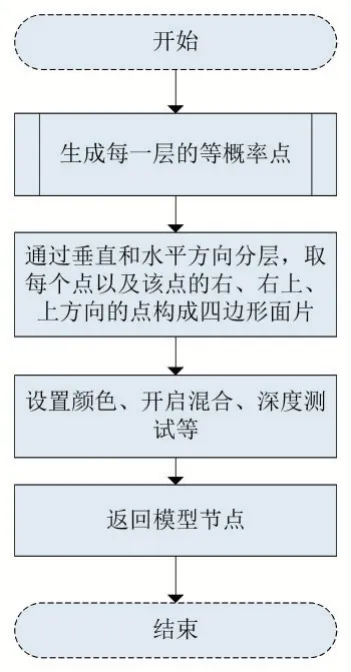
圖5

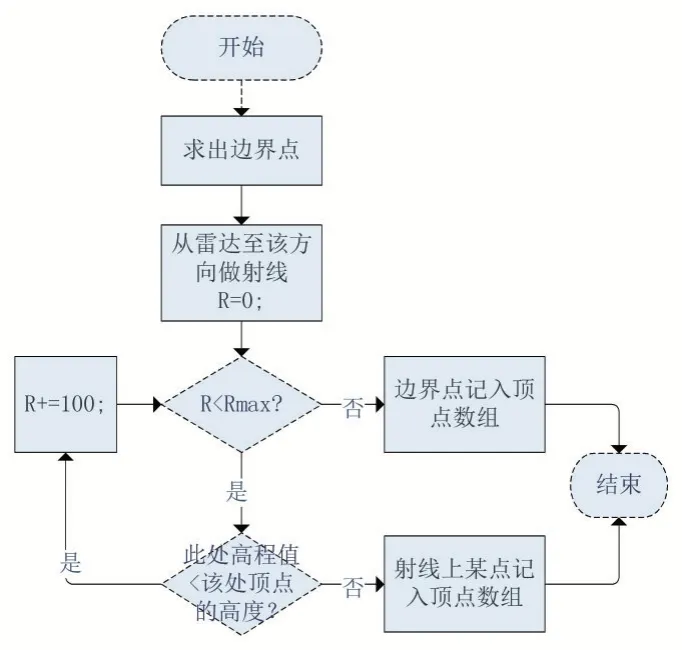
圖6

（3）大氣因素

晴朗天氣下，空氣不含惡劣天氣下的各種粒子，而主要應該考慮的是氧氣和水蒸氣的作用。它們會對吸收電磁波，造成電磁波的衰減。

如圖7 所示。

根據資料，有多種模型可以用來描述大氣的吸收作用，與之有關的因子為高度和頻率：

Libebe 模型計算吸收衰減率為[5]：

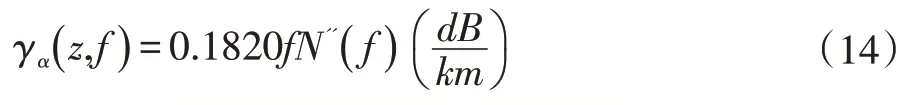
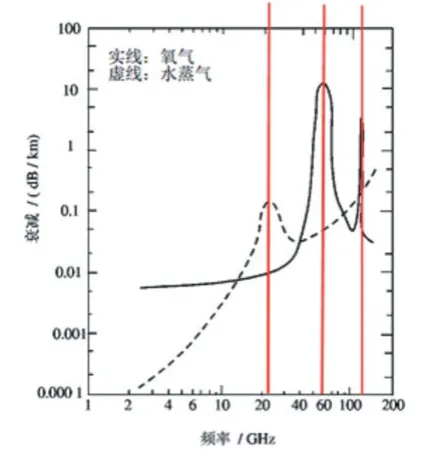
圖7 大氣衰減曲線圖[5]

ITU-R 模型將大氣吸收率表示為氧氣和水蒸汽的吸收率的和[5]：

惡劣天氣下也會對電磁波的傳播產生影響，如在不同的降雨強度下，不同頻率的電磁波的衰減程度如圖8 所示。

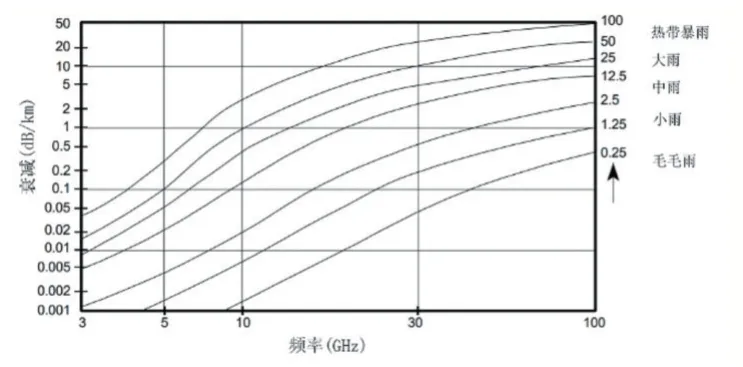
圖8 電磁波在不同降雨強度下的衰減[6]

2 結語

目前實現了在自由空間中對高斯型、SINX∕X 型的單基地雷達的最大探測范圍的可視化。定性討論了影響雷達探測范圍的因素——地形遮擋、大氣折射、大氣吸收，進行了單部雷達的探測概率的理論研究和建模。

在任意點處建造出的雷達最大探測范圍模型如圖：

高斯型雷達：

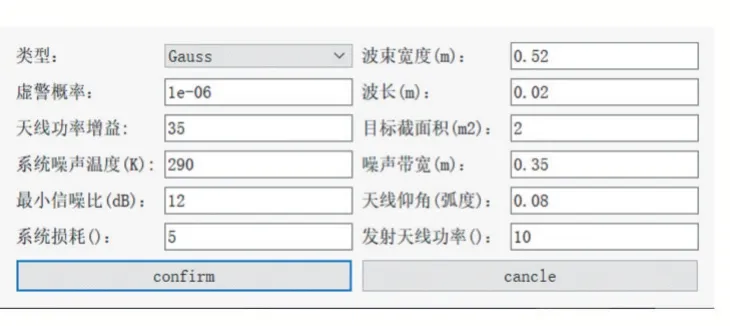
圖9 高斯型雷達參數說明

圖10 高斯型雷達最大范圍建模

SIN（X）∕X 型雷達：

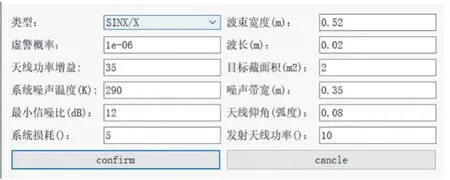
圖11 SIN（X）∕X型雷達參數說明

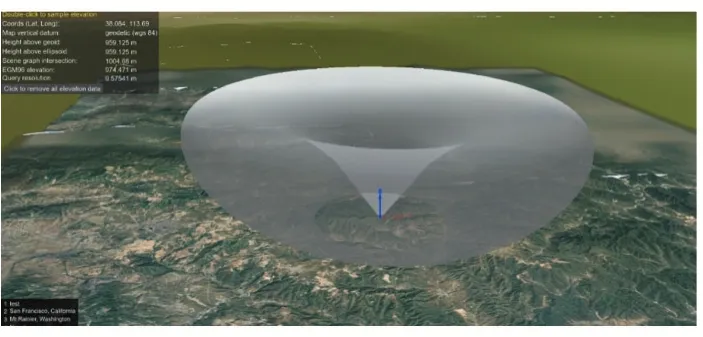
圖12 SIN（X）∕X型雷達建模

地形影響下的建模如圖13 所示。

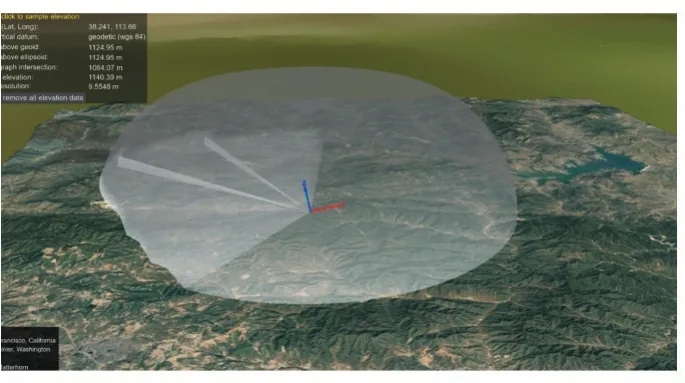
圖13 地形影響下的高斯型雷達建模

雷達的探測概率模型如圖14 所示。

圖14 雷達探測概率可視化模型

其中紅色表示概率為90%，黃色表示概率為70%，藍綠色表示概率為50%。