基于改進灰色模型的模擬電路故障預測研究

王 昊，李曠代，張曉光，李春華，沈海闊，張 朔

(1.北京交通大學 機械與電子控制工程學院，北京 100044；2.北京宇航系統工程研究所，北京 100044；3.中國船舶重工集團有限公司第七一五研究所,杭州 310023)

0 引言

飛行器信息處理設備是導彈制導系統的重要組成。在實際工況中，信息處理設備主要是對彈上采集系統采集的制導圖像進行信息處理，并將圖像處理結果同時發送給飛行控制組合和人機交互界面進行顯示。信息處理設備供電電源主要為息處理機各功能模塊提供安全電源，是一個典型的模擬電路。隨著軍用電子系統的復雜度和集成度的加速增長,我國對軍用裝備的可靠性和維修性的認知發生了很大的改變,由傳統的事后維修逐漸向視情維修轉變。在武器裝備系統全生命周期費用中，使用和保障費用高達72%，與研發使用費用相比，維修保障費用在技術上更具有可壓縮性[1]。視情維修作為一種降低維修保障費用的重要技術手段主要是通過故障預測來實現。在故障預測常用的方法中灰色理論以其小樣本、無規律樣本分布和較高預測精度被廣泛使用[2]。

1 故障預測特征參數選取

故障預測特征參數表征了被預測系統的實時運行狀況，應隨著系統的退化發生單調變化，而且在一定變化范圍內能有效區分。

信息處理設備電源模塊主要負責整個設備的電源供應，主要涉及DC/DC模擬電路，BUCK電路可實現降壓功能，是DC/DC電路中最基本的電路之一。以BUCK電路為例，在MATLAB仿真平臺下，利用Simulink建立電路模型。設定電路不同的工作條件及元器件參數，并進行電路仿真和狀態信號的采集，最終確定模擬電路采用的特征參數。

1.1 BUCK電路Simulink仿真

BUCK電路的原理如圖1所示。

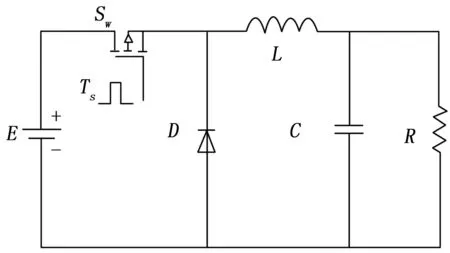
圖1 BUCK電路原理圖

其中：E為輸入電壓，Sw為MOSFET開關，Ts為周期性的矩形波，為MOSFET開關提供周期的通斷狀態。當處于高電平時，開關管處于導通狀態，電感L被充磁，流經L的電流線性增加，同時給電容C充電，給負載R提供能量。當處于低電平時，開關管處于斷開狀態，L通過二極管D續流放電，輸出電壓靠濾波電容放電以及減小的電感電流維持。

根據BUCK電路原理圖，利用simpowersystems中的模塊建立仿真模型，如圖2所示。其中IGBT/Diode模塊模擬MOSFET開關，Pulse Generator模塊產生脈沖驅動開關管，Simout模塊和Scope模塊方便讀取紋波電壓值，輸出電壓讀取有效值。

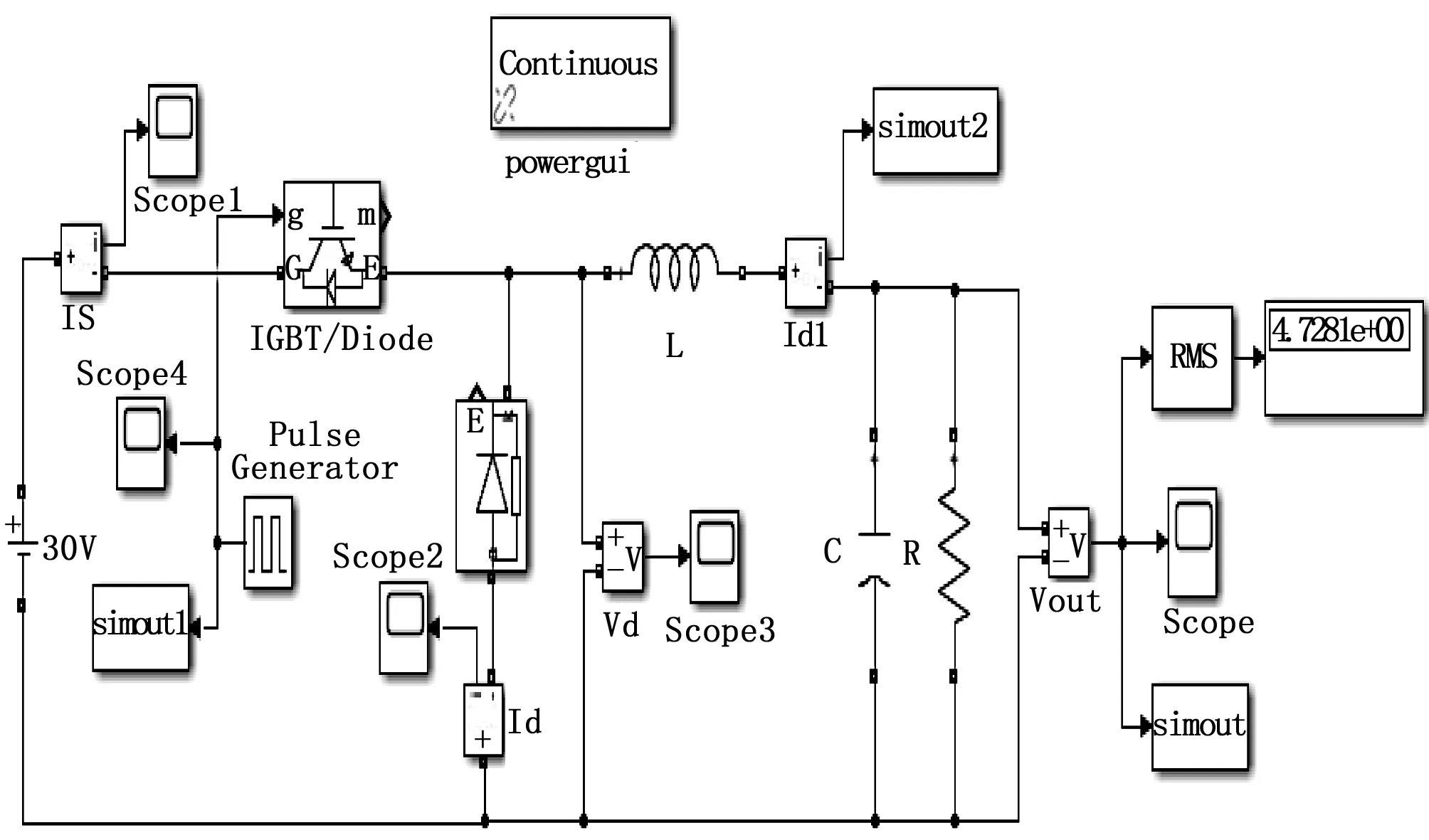
圖2 BUCK電路Simulink仿真

1.2 電路元器件初始值計算

設置初始參數，輸入電壓20 V，輸出電壓5 V，負載電阻10 Ω，工作頻率10 kHz，要求紋波電壓值不超過輸出電壓的0.5%。BUCK電路Simulink仿真模型紋波電壓的誤差應控制在10%以內，認為建立的仿真為有效模型。

根據以下公式計算仿真電路電容值C0和電感值L0。

(1)

其中：D，Ts分別為占空比，脈沖周期；V0，Vd，I0分別為輸出電壓、輸入電壓、負載電流。

由式(1)可以得出在紋波電壓小于0.025 V條件下，占空比為0.25，電容初估值為C0=500 μF，電感的初估值L0=0.375 mH。

當占空比為0.25(輸入電壓20 V，輸出電壓5 V)，工作頻率fs=10 kHz，電容C0=500 μF，電感L0=0.375 mH條件下，計算的理論紋波電壓值為0.025 V，通過示波器讀取的BUCK電路Simulink仿真模型的紋波電壓值為0.026 7 V，理論誤差為6.8%控制在10%以內，由公式(1)中計算的電感電流波動的理論值為1 A與讀取的圖像的波動值1 A相吻合，由此判斷此BUCK電路Simulink仿真模型有效。

1.3 模擬電路退化過程

仿真模型建立后，需要模擬電路各元器件的退化過程，以期找到能夠表征BUCK電路退化的特征參數。初選輸出電壓和輸出電壓紋波值為電路的特征參數。查閱大量文獻，研究電路中各元器件的理論退化模型如下：

電解電容工作時間越長，其電解液的損耗也就越多[3], J.R.Celaya等人通過試驗研究建立了電解電容的退化模型—電容減小百分比[4]，見式(2)：

△C(t)=eat-β

(2)

其中:t為電容使用時間，α、β為常數。規定當電容相對初始值降低20%時視為失效[5]。

電感線圈的溫度會隨著工作的時間增加導致電感儲能容量降低[6]。具體退化模型見式(3)：

L(t)=L0-at

(3)

其中：t為電感的工作時間，a為模型的退化參數，L0為電感的初始值。經過國內外多位研究學者的試驗，證明當L的值較初始值降低了20%時，則表明其已失效[7]。

由BUCK電路電容初始值，根據電容失效條件設計輸出電壓V0與紋波電壓△V0隨電容C變化的單因子變量實驗，MOSFET管內阻設為0.02 Ω，二極管導通內阻設為0.02 Ω,電感L0=0.375 mH。由式(2)認為當電容C0=500 μF紋波電壓值超出輸出電壓的0.5%，電路發生失效。規定當電容相對初始值降低20%時視為失效，在490～610 μF范圍每10 μF設定一個數據點，具體數據見表1。

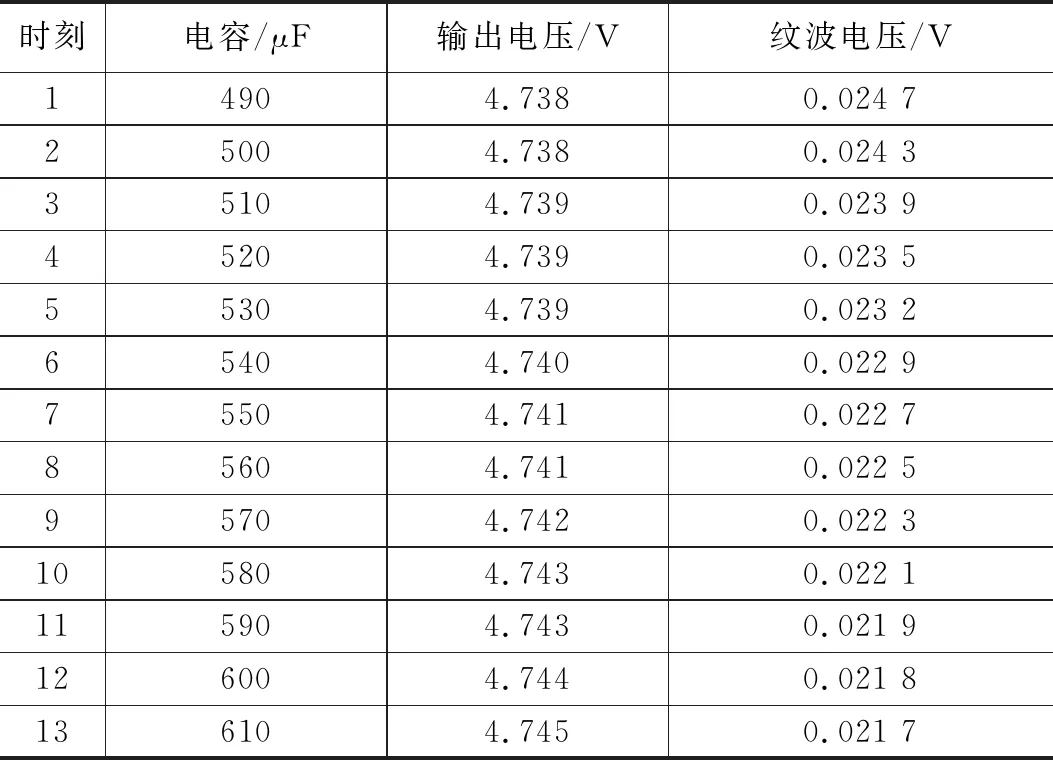
表1 特征參數與電容變化

采用最小二乘法分別對輸出電壓紋波電壓用基本函數進行擬合，擬合結果見表2。

表2 隨電容變化擬合精度

R2是擬合程度的指標，它的數值大小可以反映趨勢線的估計值與對應的實際數據之間的擬合程度，擬合程度越高，趨勢線的可靠性就越高。R2取值范圍在0～1之間，當趨勢線R2等于 1 或接近 1 時，其可靠性最高，反之則可靠性較低。從表2可以知道，隨電容變化，輸出電壓擬合結果中線性變化的R2值最接近1為0.972，可認為輸出電壓呈線性變化趨勢，紋波電壓擬合結果中指數變化的R2值最接近1為0.979。可認為紋波電壓呈指數變化趨勢。

由BUCK電路電感初始值，根據電感失效條件設計輸出電壓V0與紋波電壓△V0隨電容C變化的單因子變量實驗，MOSFET管內阻設為0.02 Ω，二極管導通內阻設為0.02 Ω,電容C0=500 μF。由式(2)認為當電容L0=0.375 mH紋波電壓值超出輸出電壓的0.5%，電路發生失效。當L的值較初始值降低了20%時，則表明其已失效，在0.375～0.460范圍每0.005 mH設定一個數據點，具體數據如表3所示。

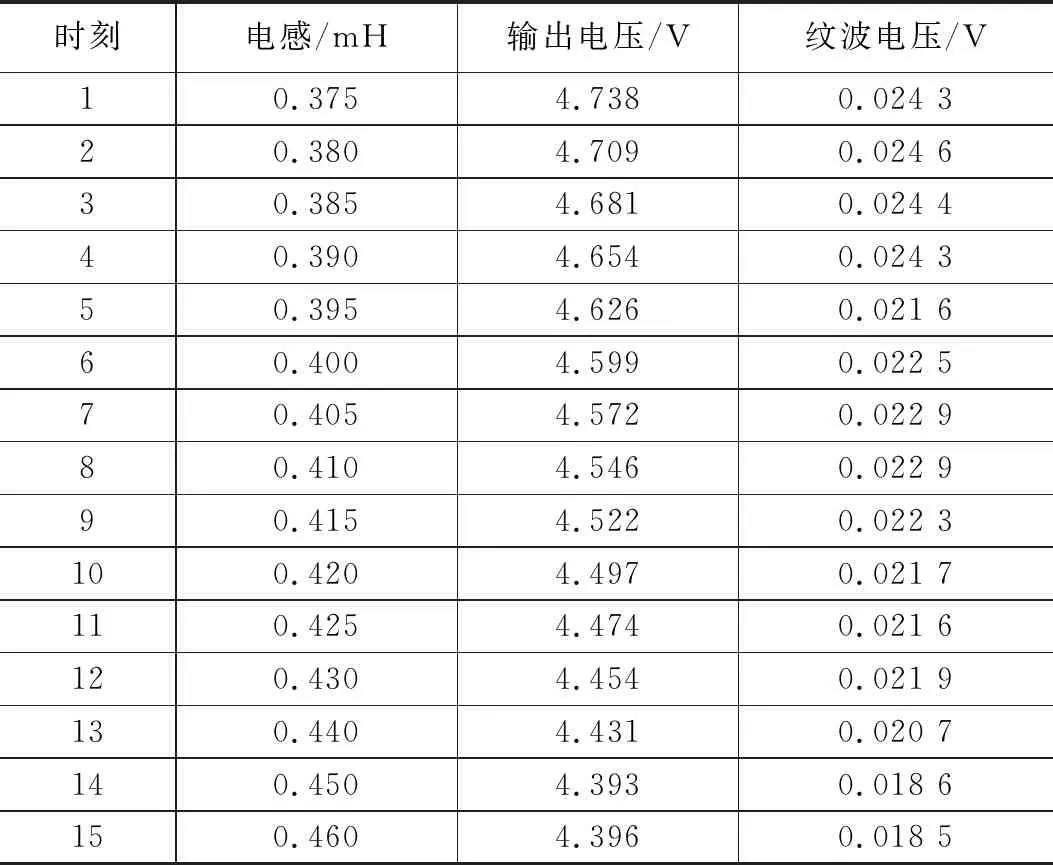
表3 特征參數與電感變化

采用最小二乘法分別對輸出電壓紋波電壓擬合，結果見表4。

表4 隨電感變化擬合精度

從表4可以知道，隨電感變化，隨電容變化，輸出電壓擬合結果中冪函數趨勢變化的R2值最接近1為0.976，可認為輸出電壓呈冪函數趨勢變化，紋波電壓擬合結果中線性變化的R2值最接近1為0.979。可認為紋波電壓呈線性變化趨勢。

綜合以上兩組單因子仿真實驗結果，參照式(2)電容退化模型和式(3)電感退化模型，紋波電壓更能反映BUCK電路退化趨勢，故選取紋波電壓作為故障預測的特征參數進行研究。

2 故障預測模型

飛行器信息處理設備供電系統的故障預測是一個典型的模擬電路故障預測，常用的故障預測方法主要有基于內建“故障標尺”的故障預測、基于失效物理模型的故障預測和基于數據驅動的故障預測[8]。分析信息處理設備供電系統的結構特點可知其中既包括已知的白色信息，也包括未知的黑色信息。基于數據驅動的故障預測中的灰色理論以其小樣本、無規律樣本分布和較高預測精度在復雜系統中被廣泛使用。所以此處選用灰色理論作為信息處理設備供電系統的故障預測模型。

自鄧聚龍教授提出灰色模型系統理論后，很多專家學者對灰色模型進行了深入的探討，結合自己研究領域提出相應的學術觀點，成功的解決了大量生產與科研中的實際問題。GM(1,N)模型是最常用的預測模型，應用也相對比較成熟，其中N表示灰色預測模型中變量的個數[9]。

2.1 GM(1,1)模型

灰色模型對原始數據的隨機性表現的比較敏感，即原始數據的粗劣程度越大，灰色模型的預測精度越低[10]。鄧聚龍教授指出：原始數據矩陣的構造對于灰色模型的建立起著至關重要的作用，由于原始數據的隨機性，會導致矩陣中某行(或某列)的數據之間產生較大差距，最終造成解的漂移。GM(1,1)模型為了解決該問題，要對原始數據序列進行數據預處理以減少序列的隨機性，增加序列的規律性。

GM(1,1)模型建模過程如下：

1)原始序列累加:

GM(1,1)模型模型一對原始序列累加生成一次，減少原始數據的隨機性，增加模型的預測精度。設有原始序列：

X(0)=(X(0)(t1),X(0)(t2),...,X(0)(tn))

(4)

則一階累加序列為：

X(1)=(X(1)(t1),X(1)(t2),...,X(1)(tn))

(5)

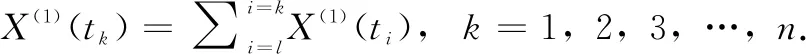
2)一階灰色模型建立：

(6)

(7)

X(0)(K+1)+aZ(1)(k+1)=u

(8)

3)最小二乘法求a，u的估計值:

(a,u)T=B-1Y=(BTB)-1BTY

(9)

4)求解預測模型:

(10)

累減生成與累加生成互為逆運算，一般用來獲取序列中相鄰數據的差值。

(11)

(12)

有時候數據序列會出現明顯的異常點，應刪除送些異常點增加序列的平滑性，但是這樣會使該序列出現空缺點。均值生成是填補該序列空缺的常用方法，稱Z(0)(tk+1)=0.5X(0)(tk+1)為原始序列緊鄰均值生成值。

2.2 改進的GM(1,1)模型

GM(1,1)模型是灰色理論中比較成熟的模型,具有建模簡單、準確的優點, 通過對建模過程進行分析，影響模型精度的因素主要有兩方面：1)數據的預處理；2)訓練模型所用數據的維數。原始數據波動性較大會導致預測模型精度降低，此外，裝備的性能退化通常被認為是一個累積過程，歷史信息包含了裝備的性能退化信息，從時間尺度上看，距裝備當前狀態時間越長的歷史信息對故障預測建模的貢獻率越低，因此，訓練模型的數據維數和建模貢獻率會影響灰色模型精度.改進的GM(1,1)模型建模過程如下：

1)原始數據平滑預處理:為了減少原始數據的隨機性和粗大誤差，增加灰色模型的預測精度，在訓練模型之前需要對訓練數據進行平滑預處理。改進模型中，選用了4種基本函數對原始數據進行平滑處理，接下來以對數函數y=ln(x+1)為例介紹處理過程：

設原始數據為X(0)=(X(0)(t1),X(0)(t2),...,X(0)(tn)

數據平滑處理后的序列為：

Y(0)=ln(X(0)+1)

Y(0)=(Y(0)(t1),Y(0)(t2),...,Y(0)(tn))

2)處理后數據一階線性累加:同式(5)，將原始數據序列編程平滑預處理后的新數據Y(0)。

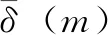
Y(0)=(Y(0)(t1),Y(0)(t2),...,Y(0)(tm0))

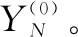
4)建立一階灰色模型同式(6)～(8)。

5)最小二乘法求解模型參數同式(9)。

6)求解預測模型同式(10)～(11)。

求得序列Y(1)后，預測序列X(1)=eY(1)-1。

3 實驗結果與分析

理想情況下 DC/DC電路的主要性能參數是規律變化或恒定不變的，但由于電路中元器件的性能退化和工作條件的變化，導致電路性能參數在電路由正常到故障過程中發生不同程度的變化，并且包含著一定的電路性能退化信息。

對飛行器信息處理設備的電源模塊等時間間隔測量了20組紋波電壓值，如表5所示。前10組數據用于訓練故障預測模型，后10組數據用于檢驗模型精度。改進的模型用Matlab編程用于輸出預測數據。

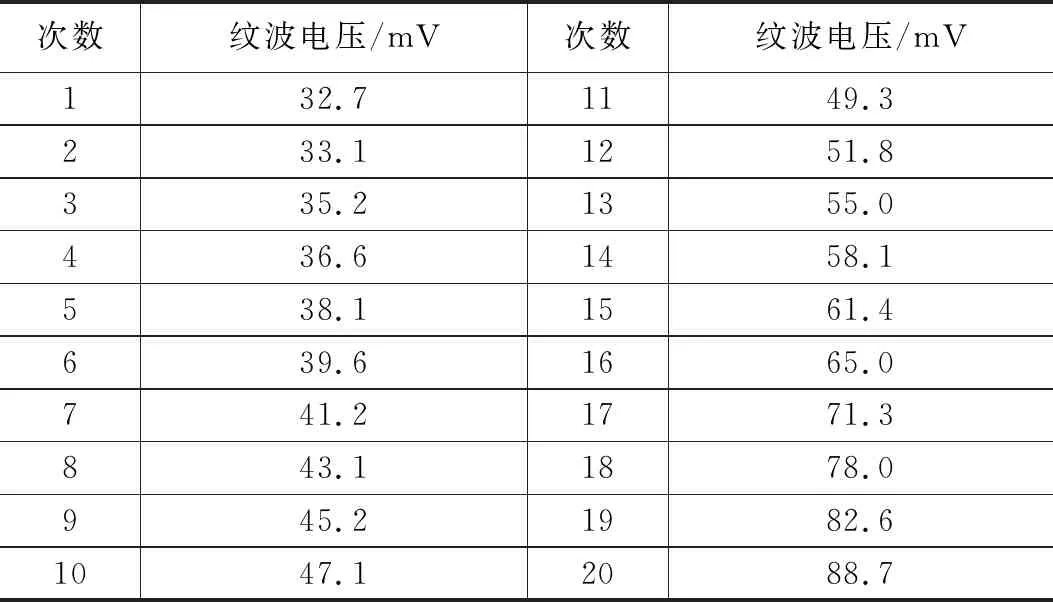
表5 信息處理設備紋波電壓值

3.1 數據平滑預處理對比實驗

前10組數據應用于GM(1,1)模型預測，數據分別采用y=ln(x+1)，y=ex-1，y=x2，y=1/x四種基本函數進行平滑預處理，求取各自平均相對殘差如表6所示，預測的10組數據繪制曲線圖如圖3所示。

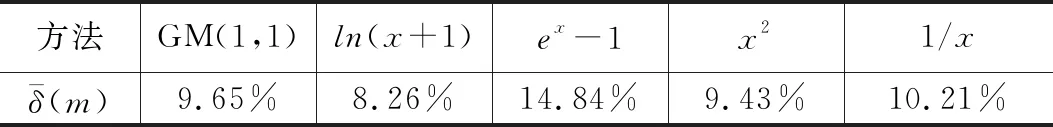
表6 預處理數據預測精度

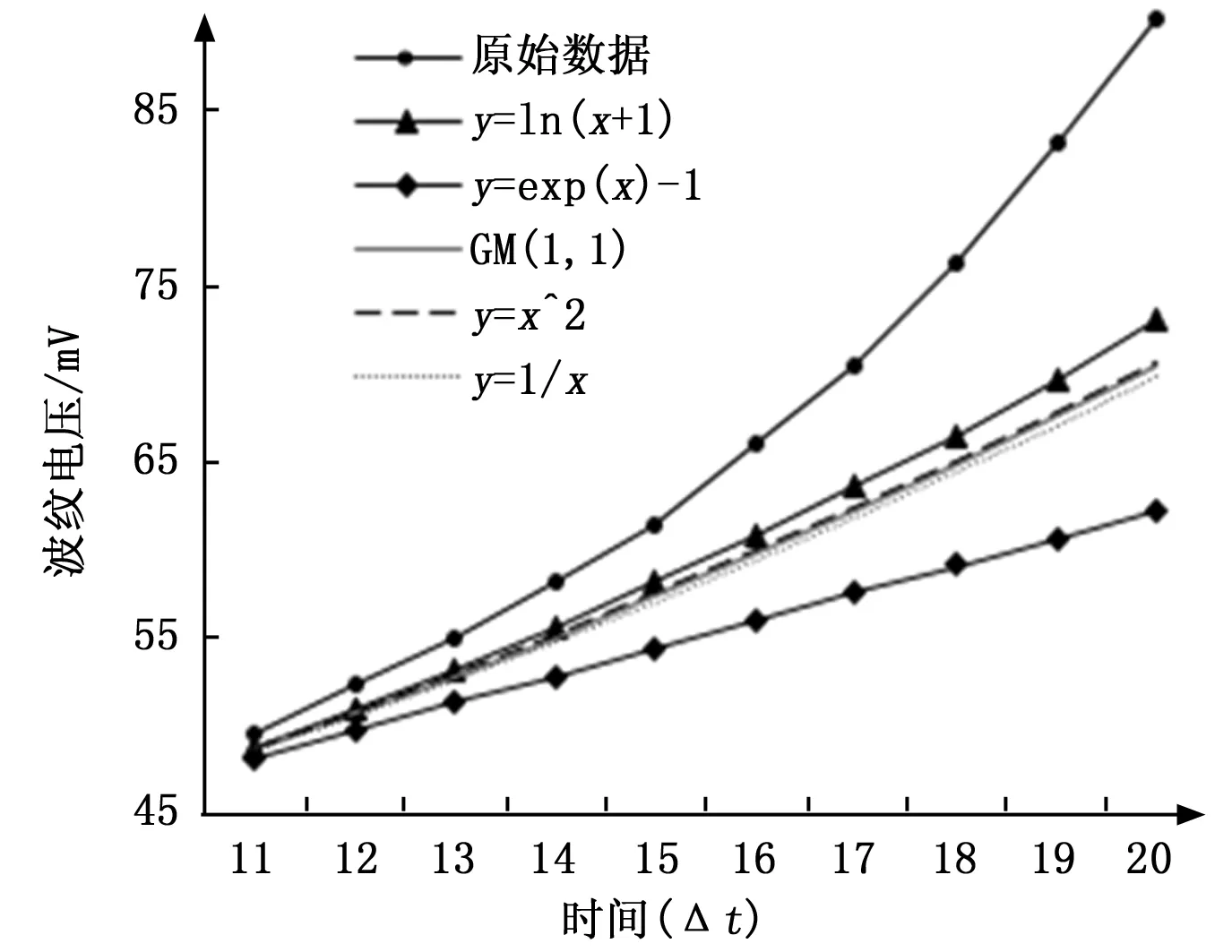
圖3 數據平滑預處理對比

從圖3中可以看出，在幾種常用的基本函數種，經y=ln(x+1)預處理后的得到的預測數據曲線相對于GM(1,1)的出的預測數據曲線更接近于原始數據。從表6中也可以看出，經y=ln(x+1)預處理后的平均相對殘差為8.26%相對于未處理的數據的9.65%有一定程度的提高。

3.2 訓練數據降維對比實驗

將用于訓練模型的10維數據通過Matlab編程采用GM(1,1)模型進行降維處理，記錄每組數據的平均相對殘差繪制預測維數與平均相對殘差曲線如圖4所示。

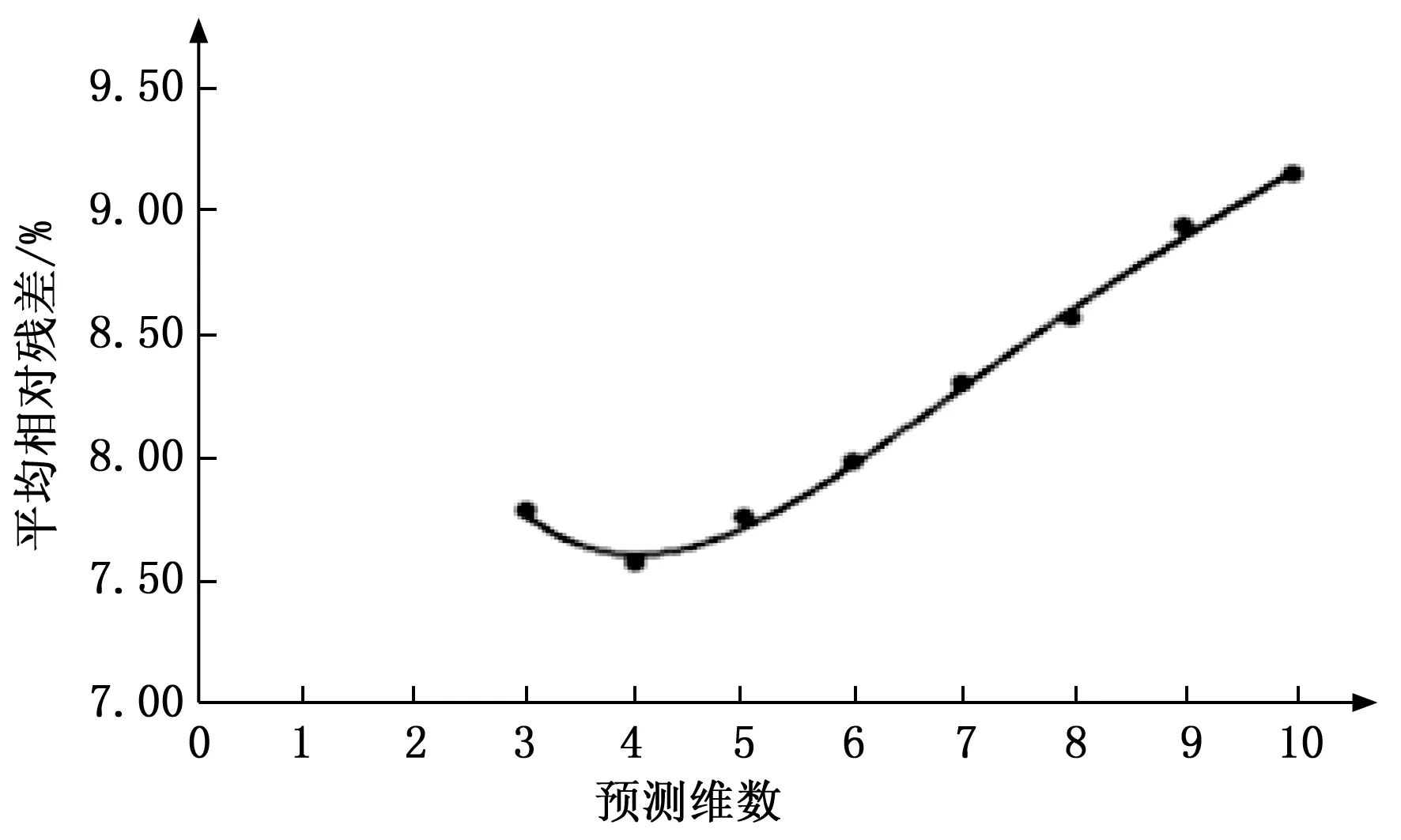
圖4 訓練數據維數與平均相對殘差關系曲線

從圖4中可以看出，當訓練數據維數降到4維的時候平均相對殘差達到最小值為7.57%預測模型的精度也最高。

綜合以上兩組實驗結果，選用y=ln(x+1)做平滑預處理，訓練數據的維數選用4維，更改Matlab程序，應用改進的具有適應度的數據平滑預處理灰色模型，并對比GM(1,1)模型，新陳代謝模型，繪制曲線圖如圖5所示。

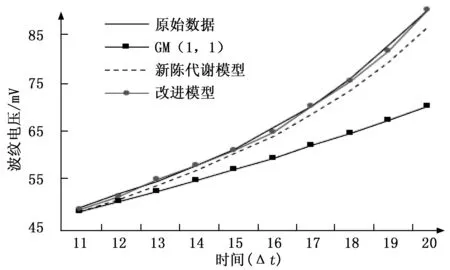
圖5 改進模型對比

從圖5中可以看出，提出的具有適應度的數據平滑預處理灰色模型的預測曲線相較于GM(1,1)模型和新陳代謝模型更接近原始數據曲線。改進后的模型平均相對殘差為0.63%，相比于GM(1,1)模型的9.65%，新陳代謝模型的2.43%預測模型精度都要高。

4 結束語

本文以典型的BUCK降壓電路為例研究模擬電路故障預測特征參數，通過Simulink仿真模擬電容電感退化過程，設計單因子變量實驗確定紋波電壓作為模擬電路故障特征參數。研究了灰色模型建模過程，從數據的預處理和訓練數據維數入手改進得到了一種具有適應度的數據平滑預處理灰色模型。結合飛行器信息處理設備電源模塊設計了數據預處理對比實驗和訓練數據降維對比實驗，結合兩組實驗結果驗證了改進模型的有效性和正確性。