基于用戶偏好矩陣填充的改進混合推薦算法

鄭小楠，譚欽紅，馬 浩，劉武啟

(1.重慶郵電大學 通信與信息工程學院，重慶 400065；2.重慶郵電大學 信號與信息處理重慶市重點實驗室，重慶 400065)

0 引 言

協同過濾推薦算法(collaborative filtering recommendation algorithm，CF)作為推薦算法中應用最普遍的算法之一，被廣泛應用于推薦系統中[1]。但是其自身的數據稀疏性[2]、相似度計算不合理等問題都導致了算法推薦質量的嚴重下降。

針對數據稀疏問題，目前大多數研究采用的是利用評分均值、眾數或者中位數等進行填充。這些同等填充方法忽略了用戶偏好和物品差異，缺乏一定的可靠性。文獻[3,4]通過研究用戶對物品的偏好程度和物品相似度對評分缺失項進行了填充。文獻[5]通過計算用戶的興趣得分進行矩陣填充，以上方法都以不同的方式降低了數據稀疏率，但未充分考慮用戶偏好和物品屬性之間的內在聯系。

針對相似度問題，文獻[6]提出了衡量物品屬性的相似度計算方法，文獻[7]提出一種基于評分和結構相似度計算物品相似度的方法。文獻[8-10]也都針對相似度計算提出了不同改進辦法。以上方法均未考慮不同目標用戶的偏好。針對以上問題，本文提出了一種改進算法，該算法考慮了用戶偏好的權重。根據目標用戶的不同，改進物品相似度的計算；最后結合改進的填充算法和相似度計算公式得到基于用戶偏好矩陣填充的改進混合推薦算法。該算法不僅大大提高了推薦的準確性，而且還滿足了用戶的個性化需求。

1 傳統的協同過濾推薦算法

首先定義用戶集合U={U1，U2，U3，…,Um}，物品集合I={I1，I2，I3，…,In}，用戶評分矩陣Rm×n，符號相關概念定義見表1。其中Rui∈[1,5]，當Rui=0時表示用戶沒有評價該物品。傳統的協同過濾推薦算法步驟如下：

步驟1 根據用戶評級數據構建用戶物品評分矩陣如式(1)所示

(1)

表1 本節公式符號含義

步驟2 根據步驟1構建的評分矩陣，計算用戶或者物品間的相似度，獲取用戶或者物品相似度矩陣。用戶相似度計算如式(2)所示，其相似度矩陣為m×m的矩陣，定義為Su，計算結果如式(3)所示。物品相似度計算如式(4)所示，其相似度矩陣為n×n的矩陣，定義為SI，計算結果顯示在式(5)中，公式相關概念的定義顯示在表1中

(2)

(3)

(4)

(5)

步驟3 對步驟2獲取的用戶或者物品相似度矩陣進行排序，得到目標用戶或物品的近鄰集合Uk或In。

步驟4 產生推薦集合。如果采用基于用戶的推薦，則可以根據用戶a的近鄰集合Uk獲得尚未評級物品i的用戶a對i的預測評級分數Pa,j，如式(6)所示

(6)

類似地，如果采用基于物品的推薦，則根據用戶的評分物品計算的推薦集合In可以獲得用戶a對沒有評分的物品i的預測評級分數Pa,i，如式(7)所示

(7)

最后根據從大到小的預測分數，獲取目標用戶a的推薦集合。

2 本文算法

2.1 融合用戶偏好的矩陣填充方法

不同用戶對不同物品屬性的偏好不同，我們稱之為用戶偏好。不同物品具有不同的屬性，且每個屬性對于區別該物品與其它物品的貢獻值不同，我們稱之為屬性權重。文獻[5]提出了融合用戶興趣評分的填充方法考慮了物品之間差異性，但未衡量不同用戶的物品屬性偏好權重。針對以上矩陣填充的缺陷，本文提出了一種基于用戶偏好和屬性權重的矩陣填充算法。該算法考慮了用戶對物品屬性的偏好，使填充的數據更可靠，并獲得更好的推薦。

不同的物品具有不同的屬性，每個屬性具有不同的權重值。用戶對不同物品的評分差異可以反映用戶對不同物品屬性的偏好。當填充矩陣時，結合評分數據，分析用戶對物品屬性的偏好，并計算用戶的偏好權重和屬性評分均值。然后利用偏好權重和屬性評分均值進行計算，計算結果用于矩陣填充，使填充值具有更好的推薦效果。

2.1.1 建立用戶偏好矩陣

本節中采用TF-IDF(term frequency-inverse document frequency)的思想，結合用戶u對電影I的評分Ru,i進行計算，計算結果代表用戶的物品屬性偏好權重。TFut在本文的含義是，物品屬性t在用戶u的已評分物品集合中出現的次數。TFut越大，表示該用戶u對物品屬性t的喜好越大，越能用該物品屬性代表用戶的喜好。IDF(t)在本文的含義是，物品屬性t在整個物品集合中出現的次數。IDF(t)越大，表示物品屬性t對區別不同用戶喜好的貢獻越少。因此本文使用下面的式(8)定義了用戶u對物品屬性t的偏好，相關公式符號含義見表2。

表2 公式含義

P(u,t)=TFut×IDF(t)

(8)

(9)

(10)

用戶對物品的評級代表了用戶對物品屬性的主觀偏好。在式(8)～式(10)中，如果物品屬性t在用戶已評分物品中經常出現，并且TFut值比較大，這意味著用戶對物品屬性t具有高度偏好，并且用戶可能更喜歡具有屬性t的物品。如果用戶評價了很多包含某一相同元素的物品，但是TFut值比較小，這就表示用戶對屬性t比較喜好，但是很難獲取到具有物品屬性t的物品。即推薦具有物品屬性t的物品給用戶更貼近用戶的需求。IDF(t)顯示了物品屬性t在整個數據集中的流行度。用它對用戶偏好進行加權可以保證實驗結果不會被流行元素影響。

最后對式(8)～式(10)進行歸一化處理，使

(11)

歸一化處理后wu,t∈(0,1)。對于用戶u，它的偏好向量為wu(wu,1,wu,2,wu,3,…,wu,m)。同理可得用戶集中所有用戶的偏好向量，進而求出用戶的偏好矩陣P(表3)。

表3 用戶偏好矩陣

由此計算出了用戶對特定物品屬性的偏好權重。

2.1.2 計算物品屬性評分

結合用戶評分數據和物品屬性信息可以構建評分矩陣(表4)和物品屬性矩陣(表5)。依據用戶的評分數據和物品屬性，能夠得到用戶對具體物品屬性的評級。

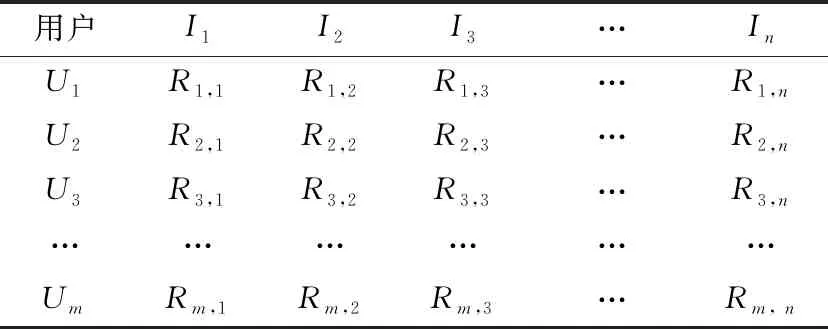
表4 用戶-物品評分矩陣

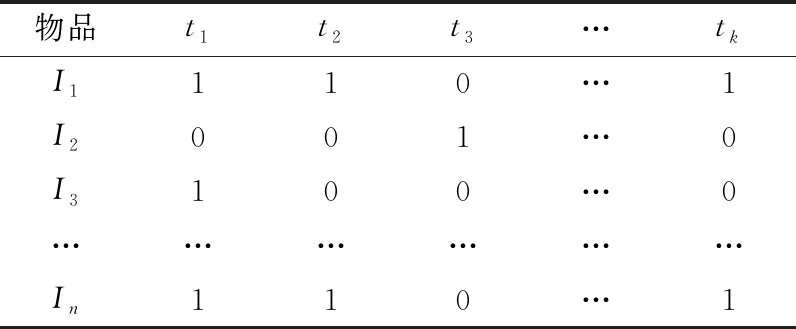
表5 物品屬性矩陣

表5中的t=1表示該屬性包含在該項中，并且t=0表示該屬性未包括在該項中。計算物品屬性的用戶評分，如式(12)所示

(12)

最后根據計算式(12)的計算結果得到用戶-物品屬性評分矩陣(表6)。

表6 用戶-物品屬性評分矩陣

2.1.3 基于用戶偏好的矩陣填充

根據表3獲取的用戶偏好矩陣和表6獲取的用戶物品屬性評分矩陣，填補用戶評分缺失項。填補用戶的未評級物品時需要考慮兩個方面：

(1)未評級物品中包括的所有物品屬性都包含在用戶已評分物品集的所有物品屬性中。在該情況下，采用式(13)計算填充值

(13)

(2)未評級物品中的物品屬性未包含在用戶的評級物品集中。在該情況下，為了避免不準確的填充值影響后續評分的準確度，不填補該物品。

通過本節提出的算法，填補用戶未評分的物品可以很好地緩解評分數據的稀疏性。最后在實驗部分對本節提出的填充算法與目前研究中常用的幾種填充算法進行對比。

2.2 考慮目標用戶的相似度計算方法

傳統的CF算法中，相似度的計算沒有考慮目標用戶不同。簡而言之，在進行相似度計算時，兩個物品之間的共同評分用戶的權重是一樣的，目標物品的近鄰對所有用戶都是一樣的。然而合理的假設是，當我們搜尋目標物品近鄰時，應該考慮對目標物品和另一物品都評過分的用戶間的相似度，為每個目標物品選擇不同的近鄰。另外，傳統的計算方法也未考慮用戶的偏好差異。因此本文提出一種考慮用戶的偏好差異的相似度算法。該算法從兩個方面改進了相似度計算公式：用戶偏好和鄰居選擇。考慮用戶偏好，根據目標用戶的不同，為每個目標項選擇不同的近鄰集合，使近鄰選擇更加合理，提高推薦的精度。

從式(3)可知，當計算兩個物品之間的相似性時，首先需要尋找對這兩個物品都評過分的用戶集合。然后根據用戶集合中的用戶的評分偏差來計算兩個物品間的相似度。對于任何用戶來說，物品之間的相似性是相同的，這顯然是不合理的。因此，本文中相似度算法改進的第一點是將用戶相似度引入到物品相似度的計算中，并在計算物品之間的相似度時，考慮目標用戶與已對兩個物品進行評分的用戶之間的相似性。然后對用戶相似度的計算要考慮用戶偏好的差異。因此本文對相似度算法改進的第二點是采用表3的用戶偏好矩陣，考慮用戶之間的偏好差異來計算用戶之間的相似性。最后，本文采用的用戶相似度的計算如下面的式(14)所示，考慮用戶偏好的物品相似度的計算如式(15)所示。其中，公式中的符號含義見表7。

表7 公式含義

(14)

(15)

2.3 基于用戶偏好和屬性權重的改進混合推薦算法

根據用戶對物品屬性的偏好權重填充矩陣，然后改進相似度計算公式。為不同的目標用戶和不同的目標物品找到更合適的鄰居集，然后根據鄰居集計算物品評分預測值。最后，提出了一種基于用戶偏好和矩陣填充的改進混合推薦算法。

算法：基于用戶偏好矩陣填充的改進混合推薦算法

輸入：用戶評分數據、物品屬性信息、鄰居數目K

輸出：目標用戶的預測評分

具體的步驟如下：

(1)計算用戶偏好和屬性評分均值；

(2)根據(1)中得到的矩陣，采用式(13)的計算結果填充矩陣；

(3)根據(1)中求解的偏好權重計算不同用戶間的相似度;

(4)根據(3)計算的結果，考慮目標用戶的差異，使用式(15)計算物品之間的相似度;

(5)根據步驟(4)得到的對于不用目標用戶的物品相似度，采用如式(16)獲取用戶沒有評分物品的預測值。最后，選擇預測值中得分最高的前N項作為目標用戶的推薦集。其符號含義見表8

(16)

表8 式(16)符號含義

3 實驗與分析

3.1 實驗準備

本文的所有實驗和算法都是通過MATLAB和Python實現。實驗運行PC的操作系統為Windows10，處理器為Intel Core i5-4200U CPU,內存為8 GB。

本文采用的實驗數據是Movielens100k數據集，該數據集是推薦算法研究中的常用數據集[11]。為了更好地對本文所提出的算法進行實驗對比和分析，選擇它作為實驗數據集。該數據集有943個用戶對1682部電影的100 000條評分數據[11]，除此之外還有用戶的基本信息和物品的屬性信息等。

3.2 評估指標

為了評估改進的推薦算法的準確度，本文選擇平均絕對誤差(mean absolute error，MAE)作為評價標準。MAE用來計算物品的預測值和真實值之間的差異，MAE值越小，說明預測值的準確度越高，其計算公式如式(17)所示

(17)

其中，n代表預測評分的個數。

3.3 結果分析

為了保證結果的準確性和可行性，本文將數據集隨機分成兩部分，80%的數據用于訓練,20%的數據用于測試。Movielens數據集由5組隨機分割的訓練集和測試集組成，這些訓練集和測試集在提供的5對數據集上執行。每個實驗取5次實驗結果的平均值進行分析。

實驗1：測試本文提出的缺失項填充算法的有效性。

通過從訓練數據中隨機選出一些已評分電影作為評分缺失項，然后分別采用用戶評分均值填充法(URA)，物品評分均值填充法(IRA)，文獻[5]提出的融合用戶興趣評分填充法(UIR)和本文的基于用戶偏好的矩陣填充法(UPR)對缺失項進行填充，最后，計算包含不同用戶的數據集下的MAE值，實驗結果如圖1所示。

圖1 常用填充算法的MAE比較

從圖1能夠看出，伴隨K值的變化，4種算法的MAE都剛開始逐步下降，然后再慢慢上升。這是因為近鄰個數的選取需要在一個合適的范圍內，過大過小都影響推薦精度。即便如此，采取本文的UPR算法填充評分缺失項的MAE值在包含不同用戶數的數據集中都比其它3種填充方法小，準確度至少提升了4.3%。說明在填補用戶評級缺失項時考慮用戶的偏好權重可以獲得更好的推薦。

實驗2：檢測改進相似度計算的有效性。

為了測試本文改進的相似度計算的有效性，本文將針對以下4種情形進行對比：

(1)計算傳統的CF算法的MAE值；

(2)在傳統CF算法上采用本文改進的相似度計算，然后再根據推薦結果計算MAE值(CF_S)；

(3)根據本文提出的填充算法采取傳統的Pearson相似度計算方法，根據推薦結果計算MAE值(UPR)；

(4)根據本文提出的矩陣填充算法采用的本文提出的相似度計算方法(UPR_S)。

然后將近鄰數分別設置為5、10、20、30、40、50、60、70、80、90進行實驗，最后根據推薦結果計算MAE值，實驗結果如圖2所示。

圖2 改進相似度算法性能比較

圖2的實驗結果表明了本文提出的相似度計算方法的可行性。不管是在常規的CF算法上還是在本文提出的填充算法上使用改進的相似度計算方法都比使用傳統的相似度計算取得更低的MAE值。在傳統算法中引入改進的相似度計算方法，性能提升了2.7%～3.2%，在本文填充算法的基礎上提升了2%。說明了本文提出的改進相似度計算方法的有效性。

實驗3：測試本文最終提出的算法的有效性

將本文提出的考慮用戶對屬性的偏好權重的改進混合推薦算法(IHRUP)和傳統的協同過濾推薦算法(UBCF)、文獻[3]提出的基于評分矩陣填充和用戶興趣的協同過濾推薦算法(PICF)、文獻[5]提出的基于用戶興趣評分填充的改進混合推薦算法(IHRIRF)分別在近鄰數設置為5、10、20、30、40、50、60、70、80、90時進行實驗對比，實驗結果如圖3所示。

圖3 4種算法在不同數量的用戶集下的MAE比較

從圖3可以看到，隨著K值的增加，上述4種算法的MAE值開始下降并最終接近穩定值。對于不同的近鄰個數，本文所提出的算法IHRUP均優于UBCF、PICF和IHRIRF算法,相較于UBCF算法，推薦性能提升了12%，相較于PICF算法，推薦性能提升了5.36%，相較于IHRIRF算法，推薦性能提升了0.8%，驗證該算法是有效的，可以進一步降低 MAE值，有效提高推薦的準確性。

4 結束語

本文針對現有的填充算法中未充分考慮用戶偏好和物品屬性內在關聯的問題以及相似度計算中存在的不合理之處提出了一種改進算法。該算法依據對用戶評分和物品屬性的分析，求解出用戶的偏好權重和屬性評分均值，并據此采用改進的填充算法填補缺失項。同時在相似度計算中，通過考慮目標用戶的差異來改進計算公式。最后通過實驗與其它CF推薦算法進行比較,結果表明本文改進的算法可以有效改善評分數據稀疏問題，充分考慮了用戶的偏好，能滿足不同用戶的喜好。