基于均勻正交螢火蟲算法的采礦船主尺度優化
卓宏明,陳倩清
(浙江國際海運職業技術學院 船舶工程學院,浙江 舟山 316021)
深海采礦船主要用于深海多金屬硫化物的開采,是深海礦物開采系統中的核心設備,技術復雜、設計建造難度大。采礦船的主尺度優化設計是采礦船總體設計中最基本、最重要的工作,直接關系到船舶的總體性能和經濟性。船舶主尺度優化是一個多參數、多約束非線性多目標優化問題,采用傳統的設計方法很難獲得多目標的最佳主尺度[1-2]。眾多學者嘗試采用各種智能優化算法進行船舶主尺度優化問題的求解,獲得了較好的效果[3-7]。但還存在收斂精度較低,易陷入局部最優解、算法參數較多,并且參數設置存在依靠經驗或反復試湊確定等問題。為此,考慮采用均勻設計與正交設計聯用的方法確定采礦船主尺度。
1 主尺度優化數學模型
1.1 設計變量與目標函數
結合深海采礦船的特點選取礦石最大裝載量時的設計水線長Lw1、設計水線寬Bw、吃水d、型深D、方形系數Cb、排水量Δ、礦石裝載量WC7個設計變量,即:
X=(Lw1,Bw,d,D,Cb,Δ,Wc)T
(1)
選取以下3方面的指標作為深海采礦船主尺度優化目標函數:船體空船質量WL最小、貨艙利用率EV最大、船體耐波性最優,即橫搖周期Tφ最大和縱搖周期Tθ最大。
船體空船質量WL主要包括船體鋼料Wh、舾裝設備Wt、輪機設備Wm。然而舾裝設備Wt、輪機設備Wm的質量為固定值無優化空間,因此,求船體空船質量WL最小即求船體鋼料質量Wh最小。將該目標函數表示為
minf1(X)=minWh
(2)
船體鋼料估算公式[8]為
(3)
式中:k1為系數,對于雙殼雙底船為1.16~1.45。
貨艙利用率EV為所需容積Vn與貨艙實有容積Va之比,其值越大其經濟效益越好,該目標函數可表示為
(4)
結核礦石所需容積Vn估算公式為
Vn=Wckc/ks
(5)
式中:kc為結核礦石(錳結核、硫化物)積載因素取0.40 m3/t;ks為容艙系數,取0.96。
貨艙實有容積Va估算公式為
Va=0.95(0.795Cb-0.098hd+0.455)×
[LCH(Bw-2b)(D-hd)]
(6)
式中:hd為雙層底高度;LCH為貨艙區長度,取0.56Lw;b為雙舷側厚度。
橫搖周期最大Tφ采用杜埃爾公式,采礦船在靜水中自由橫搖,忽略附加質量慣性矩。
(7)

其中:
A3=0.55
其中:Cw為水線面系數,Cw=0.537 5×Cb+0.447 4。
縱搖周期Tθ最大,
(8)
1.2 統一目標函數
綜合以上目標函數,得到深海采礦船主尺度多目標優化函數:
(9)
采用量綱-的量的最小偏差法,取統一目標函數為

(10)
式中:Whmin、EVmax、Tφmax和Tθmax分別為其最優解,Wh0、EV0、Tφ0和Tθ0為初始設計值。
1.3 約束條件
1)尺寸限制。
(11)
2)質量浮力平衡。
(12)
式中:WO為燃油、滑油、淡水質量。
3)初穩性高。

(13)
4)搖蕩周期。
Tφ≥11 s,Tθ≥2 s
(14)
5)直線穩定性。
(15)
式中:Lbp取Lw1。
2 算法設計
2.1 標準螢火蟲算法
螢火蟲算法(firefly algorithm, FA)的尋優主要由熒光亮度I和吸引度β兩個關鍵要素實現[9]。
I=I0×e-γrij
(16)
(17)
螢火蟲的位置更新式為
xi=xi+β×(xj-xi)+α×(rand-1/2)
(18)
式中:I0為螢火蟲的最大螢光亮度;γ為光強吸收系數;rij為螢火蟲i和j之間的空間距離;β0為最大吸引度即光源處的吸引度;α為步長因子,rand為(0,1)的隨機數。
2.2 均勻正交螢火蟲算法及其實現


表1 均勻設計表與均勻設計試驗方案
再通過在均勻設計獲得的初步優化參數組合的基礎上,上下浮動取值進行正交試驗及結果數據極差分析就可以獲得最優參數組合。
在有限的計算開銷中,對螢火蟲初始種群在可行域內進行均勻分布,使最有代表性的個體作為初始種群。求解問題的維度對應均勻設計中的因素,維數對應因素的個數s;各螢火蟲在各維度上的空間位置,對應于每個因素的水平,螢火蟲數對應水平數n。均勻設計表Un(ns)同樣采用好格子點法和優化中心化偏差CD值算法構造。
以優化2維的Rastrigin函數,其數學表達式為
(19)
在搜索空間[-5,5],說明均勻正交螢火蟲算法的具體實現步驟及對比性能測試。Rastrigin函數為極易陷入局部最優的多峰函數,理論最優為0。
步驟1。依據表1均勻設計表U10(104)與均勻設計試驗方案,對螢火蟲算法進行均勻設計數值實驗,結果見表2。從表2可見,第2組試驗所得的最優解最小,并且收斂較快。獲得初步優化算法參數組合為螢火蟲數量n=60;步長因子α=0.1,光強吸收系數γ=5,最大迭代次數T=200。

表2 均勻設計試驗結果
步驟2。在均勻設計基礎上進行正交設計試驗獲得最優算法參數組合。以均勻設計2號試驗獲得的各算法參數為基準,進行上下浮動取值,按正交設計表L9(34)設計4因素,3水平正交試驗,因素水平表見表3,具體正交試驗方案及試驗極差結果分析見表4。

表3 正交設計因素水平表

表4 正交設計試驗方案及結果分析
從表4中正交試驗極差分析,根據極差大小得到算法參數中各參數對函數最優解的影響主次順序γ>α>T>n,即光強吸收系數和步長因子對結果影響較大,而最大迭代次數和螢火蟲數量影響較小。正交試驗的最優水平組合為n2α3γ3T2即螢火蟲數量n=60;步長因子α=0.2,光強吸收系數γ=7,最大迭代次數T=200。將獲得的最優算法參數組合進行數值試驗驗證,獲得的函數最優解為4.7×10-4,優于正交試驗方案和均勻設計方案中的所有解。
步驟3。螢火蟲初始種群在可行域內進行均勻分布操作。二維求解空間及根據前面獲得的螢火蟲種群數量60,即共2個因素,每個因素60個水平,同樣用好格子點法來構造均勻設計表U60(602),該中心化偏差值為0.010 2,均勻性較好。根據構造的該均勻設計表確定初始種群各螢火蟲的空間位置見圖1,而常規的隨機初始種群見圖2,可見經過均勻設計分布操作后,初始螢火蟲在求解空間內分布更合理均勻。
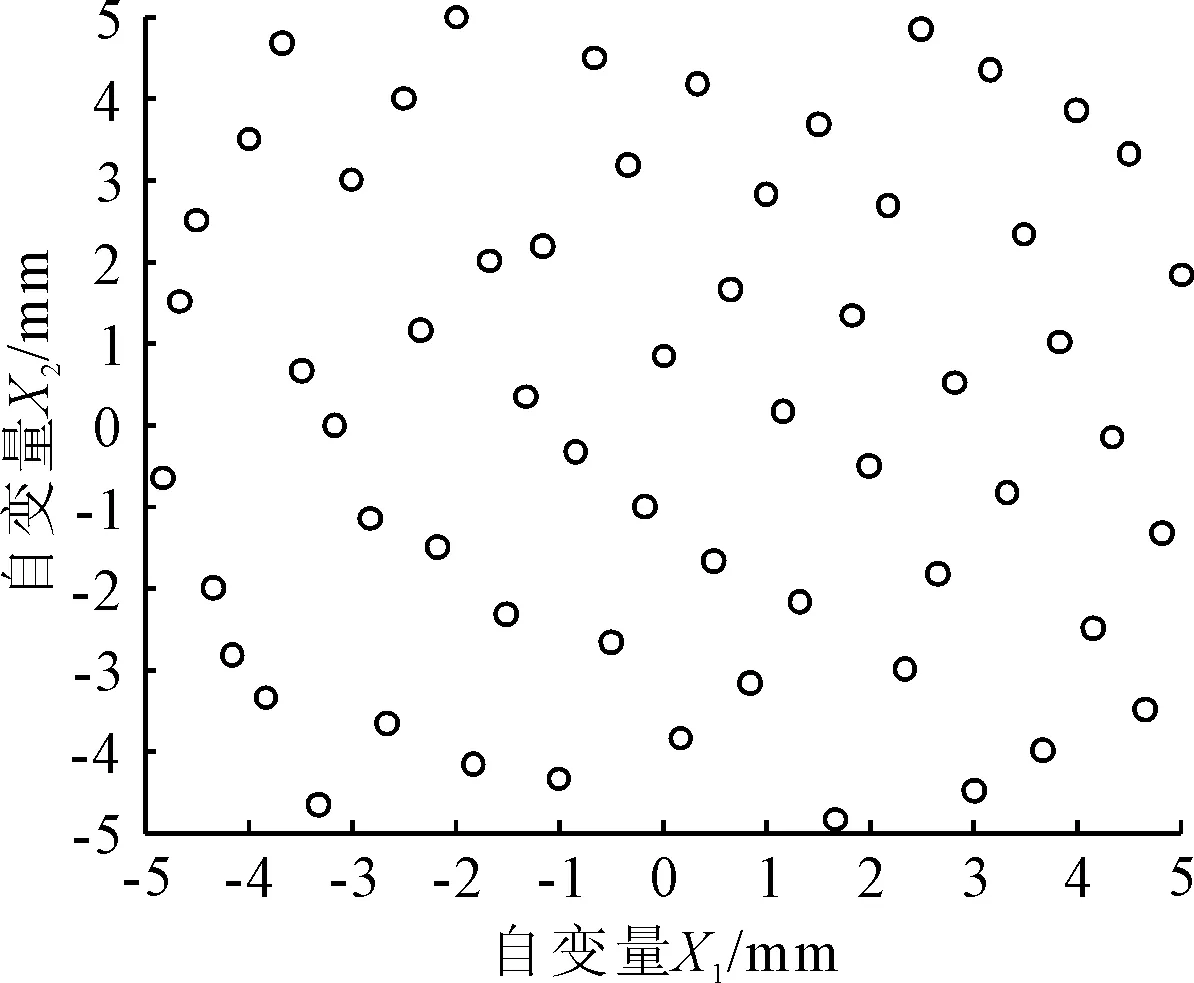
圖1 均勻設計分布的初始種群

圖2 隨機初始種群
步驟4。螢火蟲算法開始尋優迭代計算。用式(16)、(17)計算相對亮度、吸引度,確定移動方向。用式(18)更新螢火蟲位置,不斷迭代尋優。達到最大迭代次數后,輸出最優值。獨立運行10次取平均獲得的函數收斂曲線對比,見圖3,均勻正交螢火蟲算法(UOFA)的求解性能明顯高于標準螢火蟲算法(FA)。

圖3 算法收斂曲線對比
3 主尺度優化結果
采用均勻正交螢火蟲算法求解采礦船多目標優化數學模型。編碼方式直接采用代表各變量的實際值實數編碼,各變量的值即為螢火蟲在各維度的位置,主尺度優化模型共有7個設計變量,故每個螢火蟲編碼長度為7,模型的求解空間為7維。根據前面的均勻正交螢火蟲算法步驟進行逐步求解,獲得該求解數學模型的最優參數組合為螢火蟲數量n=100;步長因子α=0.2,光強吸收系數γ=2,最大迭代次數T=1 000。7維求解空間及螢火蟲種群數量100,即共7個因素,每個因素100個水平用好格子點法來構造均勻設計表U100(1007),并根據該表確定螢火蟲初始種群的空間位置,再進行算法迭代優化,求解收斂曲線見圖4,并增加了標準螢火蟲算法FA和遺傳算法GA來對比。標準螢火蟲算法FA采用相同種群數量及最大迭代次數,其他參數選用經驗值,步長因子α=0.2,光強吸收系數γ=1。遺傳算法采用相同種群數量及最大迭代次數,其余參數選用經驗值,交叉概率為0.8,變異概率為0.01[11]。設計變量初始值及優化結果見表5。

圖4 求解算法收斂曲線比較

表5 變量初始值及優化結果
結合圖4及表5,均勻正交螢火蟲算法UOFA求解模型時初始解比標準螢火蟲算法FA和遺傳算法GA都好,并且迭代10次左右均勻正交螢火蟲算法和遺傳算法都已經收斂,而標準螢火蟲算法迭代400次左右才收斂。最終獲得的統一目標函數的求解結果:均勻正交螢火蟲算法最小為1.379 7,優于標準螢火蟲算法2.004 1,也略優于遺傳算法獲得的1.404 9。最終獲得的船體鋼結構重量Wh為8 747 t比原設計減少約4.7%,貨艙利用率EV為0.443 5,比原設計提高了約46%,橫搖周期Tφ為16.35 s,縱搖周期Tθ為10.22 s,分別比原設計提高了約47%和14%,使得采礦船更加平穩。均勻正交螢火蟲算法可以對采礦船主尺度優化多目標模型進行求解,獲得滿意的方案,并且求解精度和效率均得到了提升。
4 結論
1)采用均勻正交螢火蟲算法求解采礦船主尺度多目標優化模型,獲得了滿足約束條件下的統一目標函數的滿意解。優化后的各主要指標都優于原設計,船體鋼結構重量Wh減少約4.7%,貨艙利用率EV提高了約46%,橫搖周期Tφ和縱搖周期Tθ提高了約47%和14%。
2)通過算法參數的均勻設計及正交設計獲得最佳算法參數,并對螢火蟲初始種群在可行域內進行均勻分布操作的均勻正交螢火蟲算法可以提高標準螢火蟲算法的收斂速度和精度。

