風力發電機組最優槳距角自尋優控制算法設計
蘭杰, 林淑, 莫爾兵, 王其君
(東方電氣風電有限公司, 四川 德陽, 618000 )
0 引言
風能作為一種清潔可再生能源, 越來越受到世界各國的重視。 其蘊藏量巨大, 全球風能資源總量約為2.74×109MW, 其中可利用風能為2×107MW[1]。在風電大規模發展的今天, 機組運行效率越來越受到關注。 但目前風力機風能利用效率較低,對其發展極為不利。 當前, 如何充分利用風能資源實現風電機組發電量最大化是風電場運行過程中亟待解決的問題。 目前最行之有效的方法是通過有效控制策略使風電機組運行在最優狀態來最大限度地捕獲風能, 達到風電機組發電量最大化的目的, 該方法與其他方法相比更具有有效性和可行性。
文獻[2-4]簡述了風力發電機組最大功率跟蹤控制策略; 文獻[5-7]提出了風力發電機組最大風能追蹤及變槳控制;文獻[8]提出了基于支持向量和微分進化算法的風電機優化運行, 實現了風機出力最大化; 文獻[9]提出了基于微分跟蹤器的功率曲線自尋優控制策略, 提高低風速區域對風能的利用。 然而以上傳統的最大風能捕獲控制方法通常存在一些弊端, 風力機槳距角常常被假定控制在其最優值來使風力機的功率系數最大, 實際情況而言, 風力發電機組葉片在設計、 制造、 現場安裝和實際運行過程中, 可能出現以下情況: 即葉片設計過程中, 理論最優槳距角和生產圖紙有誤差; 葉片制造過程中, 制造誤差或者葉片零刻度盤位置貼錯; 葉片現場安裝過程中, 葉片零位未與輪轂零位對齊; 葉片經過較長時間運行后,氣動性能發生改變, 最優槳距角不再是模型設計時的最優槳距角; 此外, 運行人員操作過程中產生的錯誤等。 上述使得最優槳距角偏離的原因是很難避免的, 且在實際風力機中并不是一個固定的偏移量, 不同風機可能有不同的偏差值, 很難用同一個偏移修正量去修正。
為快速、 有效尋找最優槳距角, 本文以國產某1.5 MW 機組為基礎, 充分利用其數據之間的相關性, 設計出一種自動尋優控制算法, 構造出槳距角評價函數, 能夠自動尋找出實際的最優槳距角, 為提高風力發電機組性能提供了科學依據。
1 風力機能量轉換原理分析
風力機將風能轉化為機械能并帶動發電機發電, 為實現風電機組變速運行, 追求最優Cp曲線。 Cp(λ,β)為風輪的利用系數, 反應了風力機利用風能的效率, 它是葉尖速比與槳葉節距角的函數。 根據文獻[10]風輪的尖速比經驗公式為式(1):
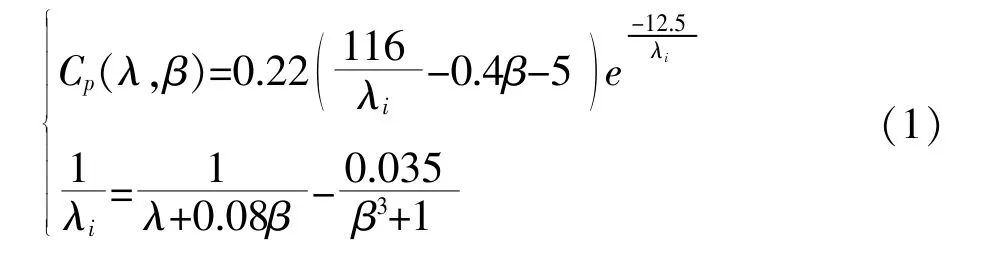
一般通過改變發電機扭矩控制發電機轉速,由風力發電機組能量轉換系統(見圖1)可知:

圖1 能量轉換系統
為使風輪運行在最優轉速上, Ωopt有如下轉換方式:
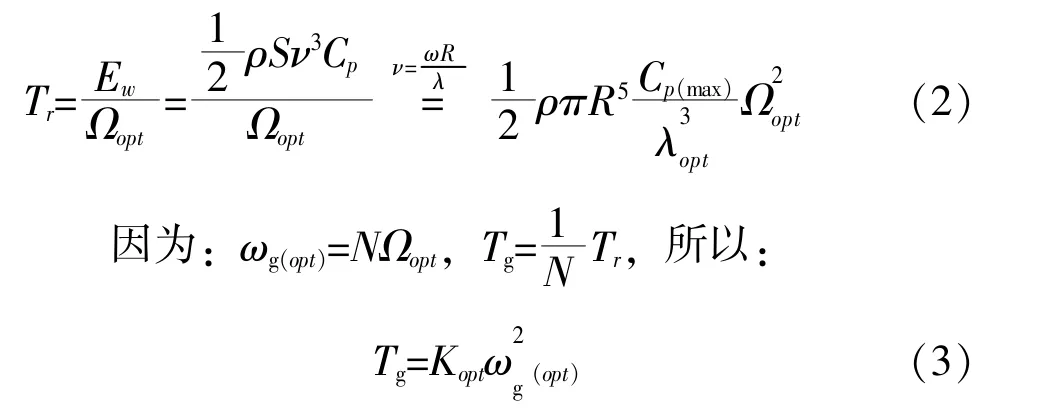
式中: Ωopt為風輪最優轉速; λopt為最優葉尖速比; Cp(max)為最優風能利用系數; ωg(opt)為最優發電機轉速; N 為齒輪箱變速比; Tg為發電機轉矩;Kopt為最優模態增益。
式(3)說明, 只要將發電機轉矩按照轉速的二次方進行設置, 便能實現最優轉速運行, 使風電機組運行在最優Cp曲線上。
為了能夠自動尋找最優槳距角, 需要得到在不同槳距角下的功率曲線, 如圖2 所示, 從而進行對比, 得出最優槳距角。
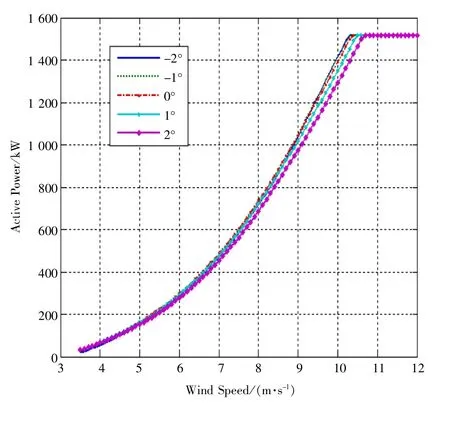
圖2 不同槳距角時的功率曲線
但是實際測量過程中, 10 min 平均風速, 很難完全一樣, 即使平均風速一樣, 由于其湍流強度不同, 可能會導致測量到10 min 平均功率不同, 通過Bladed 仿真結果如表1~3 所示。
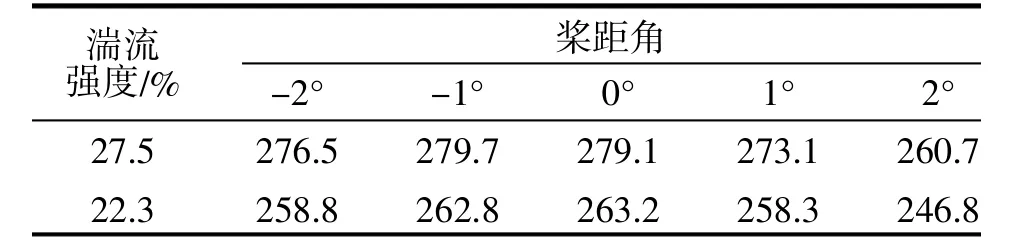
表1 平均風速5.8 m/s 時10 min 平均功率(kW)對比

表2 平均風速6.0 m/s 時10 min 平均功率(kW)對比
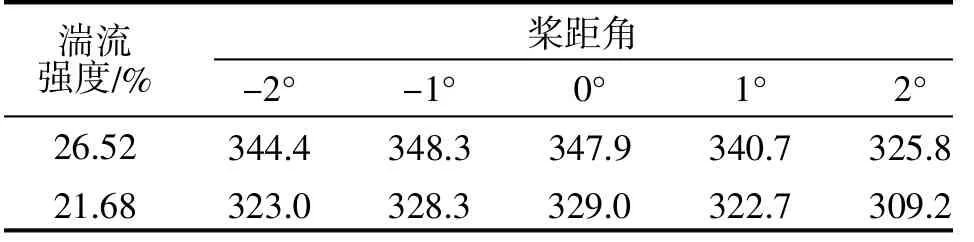
表3 平均風速6.2 m/s 時10 min 平均功率(kW)對比
從表1~3 可以得出如下結論:
(1)相同最優槳距角,不同平均風速時,10 min平均功率差別很大;
(2)相同最優槳距角, 相同平均風速下, 不同湍流強度下, 10 min 平均功率有差別;
(3)不同湍流強度, 最大平均功率所對應的最優槳距角不同;
綜上, 不能簡單以平均風速所對應的平均功率大小來簡單評判最優槳距角, 在風機運行過程中, 很難有完全相同的工況, 即相同的平均風速和相同的湍流強度。 為了達到有效的功率曲線,需要累積足夠多的樣本, 因而需要較長時間的測試運行, 才能得出較合理的統計功率曲線。 為了降低所需樣本數量, 減小測試運行時間, 應該綜合考慮湍流強度、 平均風速的影響。
2 理論分析
針對風力發電機組, 當風機葉片最優槳距角設置為不同值時, 其理論功率值也會不同, 具體如表4 所示。

表4 不同槳距角時的理論功率(kW)
從表4 可以看出, 槳距角不同時功率曲線具有以下特點:
(1)變速運行階段為5~8.5 m/s, 此時0°為最優槳距角;
(2)其余風速情況下槳距角為0°時功率曲線并不是最大。
進一步通過現場實測數據分析, 可以發現一段時間內(通常選取為10 min)風速的分布近似具有正態分布特性, 結果如圖3 所示。
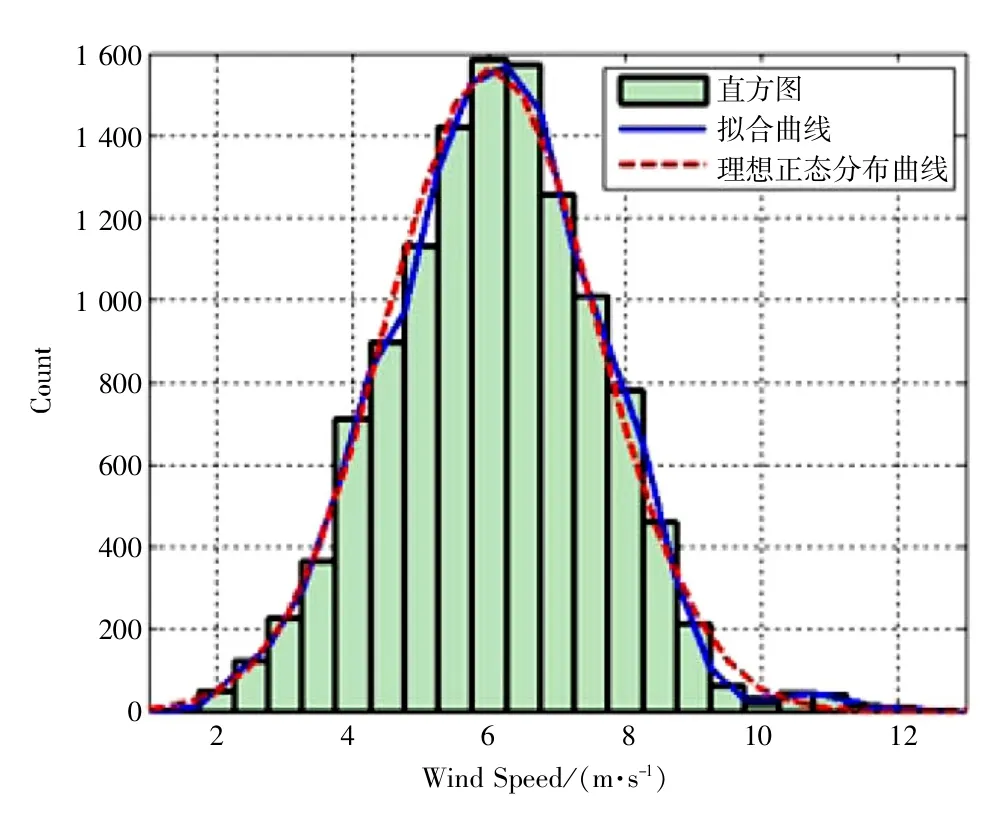
圖3 風速分布曲線
因此, 可以用正態分布來表示風速的分布情況, 也可以通過計算風速的平均值和方差來表征風速的分布情況, 即:
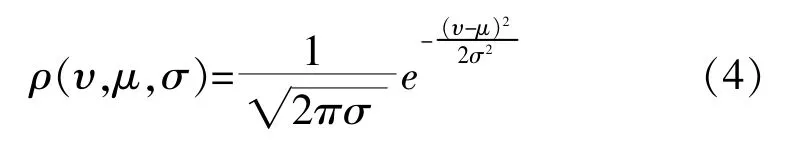
式中: υ 為風速; μ 為均值; σ 為方差。
假定風力發電機組工作在最佳狀態, 風速和功率呈對應關系, 則可以用如下積分來表達一定平均風速、 方差下的理論平均功率:
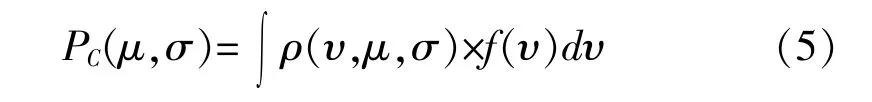
式中: υ, μ, σ 意義與式(4)相同;f(υ)表示風速對應功率函數。 典型的靜態功率曲線f(υ)如圖4所示。
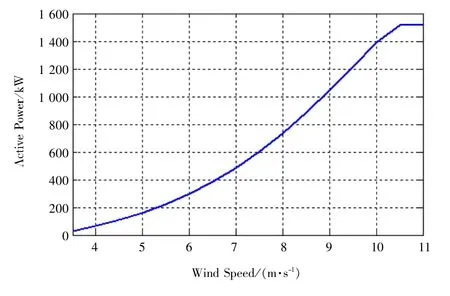
圖4 典型功率曲線
由式(5)就可以計算出對應平均風速和方差下的理論平均功率PC(μ,σ), 其計算結果也就包含了湍流信息。 而實際平均功率PM(μ,σ)也包含了風速湍流信息, 因此通過PC(μ,σ)和PM(μ,σ)構造新的評價函數, 來自動尋優最優槳距角。
3 自尋優算法設計
考慮到實際運行風機大多采用機械式風速儀測量風速, 由于其受葉片尾流影響, 得到風速具有較大誤差, 而測量到功率相對較為準確, 因此做如下假設:
風速測量具有固定偏差, 則實際風速為:

式中: υA為實際風速; υM為測量風速; Δυ 為風速測量偏差。 因此通過υM得到的平均風速也具有偏差Δυ, 但計算得到的方差卻無偏差, 即:

式中: μA為實際平均風速; μM為測量平均風速; σA為實際風速方差; σM為測量風速方差。
功率測量較為準確, 因此實際功率為:

式中: PA為實際功率; PM為測量功率。
假設構造的評價函數為F (PC,PM), 該函數也是μA和σA的函數, 即H(μA,σA), 因此把式(7)帶入可得:
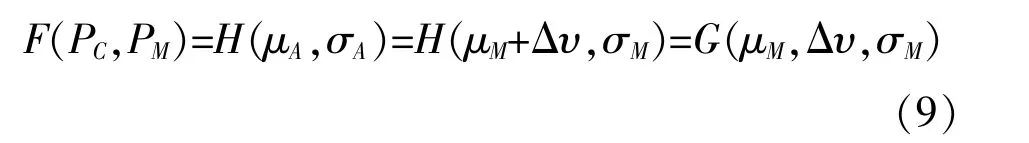
而構造的評價函數G(μM,Δυ,σM)需具有一定的穩定性, 即當Δυ 在一定范圍內波動時, 通過評價函數能得到相同的結果。 由式(5)可知, 積分是一個超越函數, 沒有一個簡單的Δυ 與F(PC,PM)的關系, 因此直接構造PC(μ,σ)和PM(μ,σ)評價函數難度很大。
考慮從測量準確的功率和風速方差出發, 計算出在方差σ 已知時, 發出電功率為P 時所需的平均風速μC為多大, 因此μC中也含有方差的信息, 再通過構造包含μC和μA的評價函數即可, 因此最終構造的評價函數如式(10)所示:
由式(10)定義很容易推得, 當評價函數更大時, 對應的槳距角為更優的槳距角。
把式(7)帶入式(10)可得:
進一步分析計算結果的穩定性, 設:
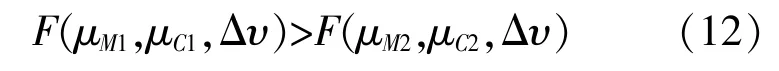
把式(11)帶入式(12)可得:
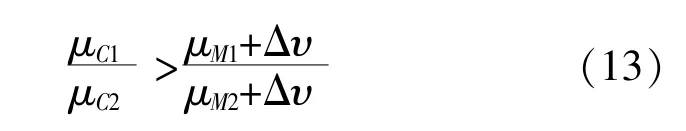
從式(13)可以看出, 當測量風速的固定偏差在一定范圍內時, 利用連續函數的保號性, 可以得到以下等價關系:
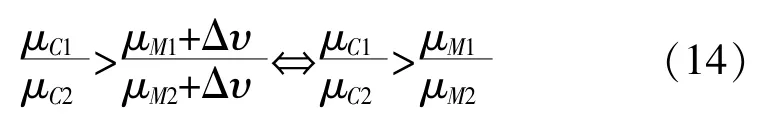
因此Δυ 在一定范圍變化時, 式(9)所定義的評價函數則是穩定的。
具體的自尋優控制框圖如圖5所示。
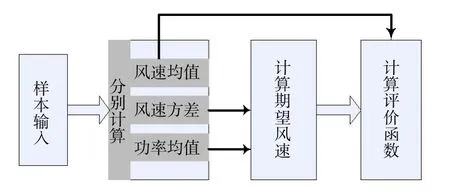
圖5 自尋優控制框圖
為了能夠完成槳距角自動尋優, 需要能夠自動調整最優槳距角, 再按照圖5 所示算法計算所有可能成為最優槳距角的評價函數, 最終得出實際的最優槳距角。 其算法流程如圖6 所示。
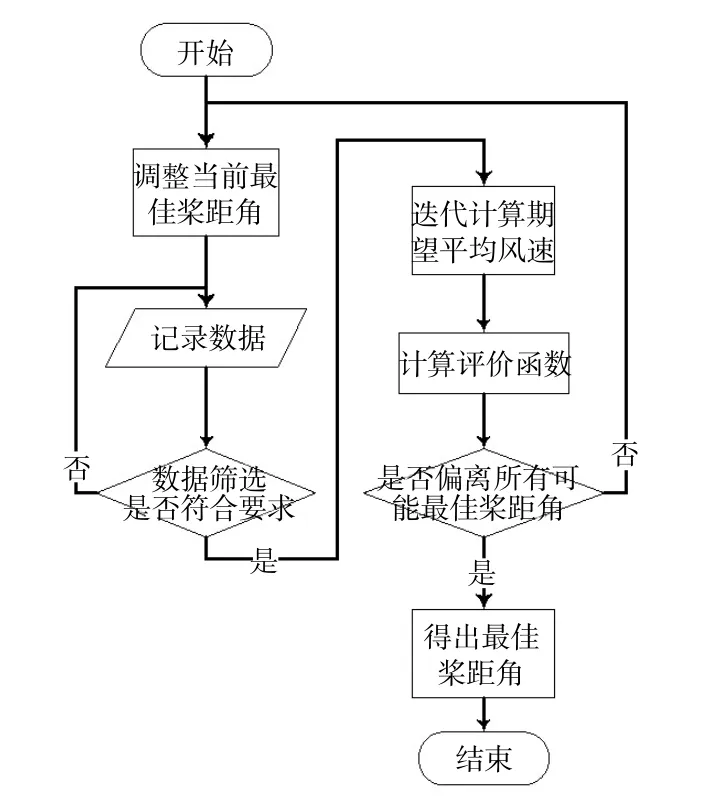
圖6 自動尋優流程圖
4 仿真分析
本文采用某國產1.5 MW 風力發電機組, 建立Bladed 模型, 模型假設最優槳距角為0°。 通過設置槳距角到分別在0°、 ±2°, 且在不同工況下進行仿真驗證對比, 仿真結果如表5~8 所示。
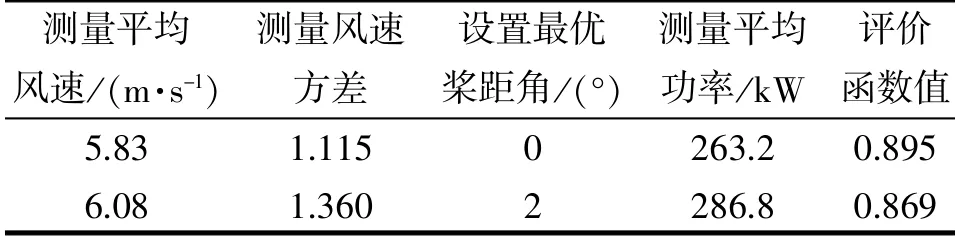
表5 結果對比1
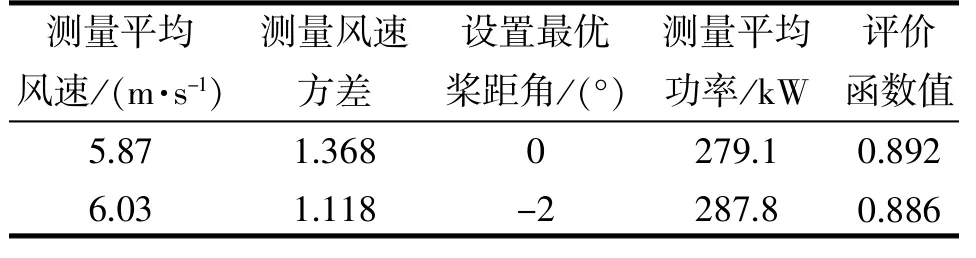
表6 結果對比2
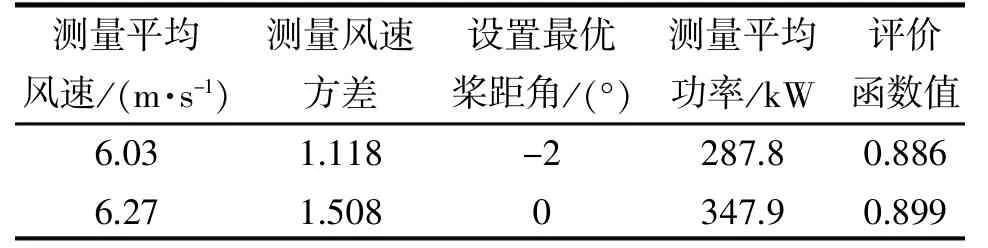
表7 結果對比3
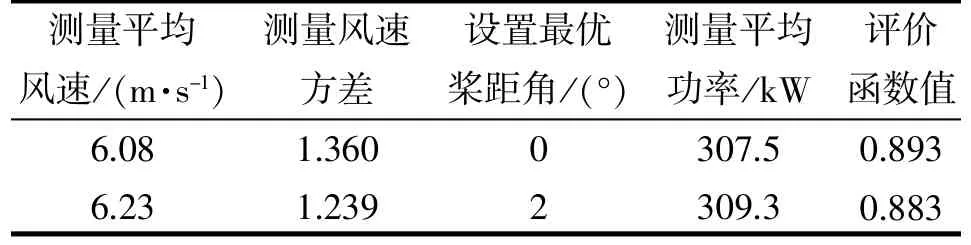
表8 結果對比4
從表5~8 可以得出, 當設置最優槳距角為0°時, 均具有最大的評價函數計算值, 因此尋優結果得出0°為最優槳距角, 而模型假定最優槳距角確實為0°, 驗證本文設計的自尋優算法能夠準確尋找出實際最優槳距角, 證明該算法的有效性、快速性, 為提高風力發電機組的性能提供了科學的指導。
5 結論
本文以國產某1.5 MW 風力發電機組設計為例,仿真結果表明, 所提出的自尋優控制算法能夠自動尋找出實際的最優槳距角, 為提高風力發電機組的性能提供了科學的指導。

