質子交換膜燃料電池微擴散層孔隙結構與滲透率的孔隙尺度模擬

何玉松， 白敏麗， 郝 亮

(大連理工大學 能源與動力工程學院， 遼寧 大連 116024)

質子交換膜(PEM)燃料電池作為一種把燃料中的化學能通過電化學反應直接轉換為電能的發電裝置，以其高效率和零排放的優點引起了世界范圍內的日益關注.PEM燃料電池主要由聚合物膜和位于膜兩側的兩個電極(陽極和陰極)組成，每個電極分別包括了雙極板、氣體擴散層(GDL)、微擴散層(MPL)和催化層(CL).其中，MPL連接了GDL和CL，對降低GDL和CL之間的接觸電阻、減緩CL降解以及提高電池耐用性和穩定性等方面均起著重要作用[1-7].此外，MPL還可以有效改善燃料電池的水管理，因此探究其傳輸特性是PEM燃料電池研究中的一個熱點.

MPL是用碳黑粉末和聚四氟乙烯(PTFE)的混合物制備的多孔介質，通常噴涂在GDL上.MPL具有復雜的微孔隙結構.此外，MPL具有最佳厚度，以平衡傳質阻力與接觸電阻[3].改善PEM燃料電池水管理是引入MPL的一個重要原因.Deevanhxay 等[4]使用高分辨率X射線照相技術對MPL中液態水的傳輸進行了原位觀察，發現液態水主要通過MPL中的裂縫被輸送到GDL.但另一方面，裂縫卻降低了MPL的機械性能，因此Chun 等[5]實驗研究了通過消除表面裂紋來改善MPL的機械穩定性.MPL的孔隙結構主要由碳黑用量、PTFE用量和制備過程控制，并直接決定了MPL的宏觀傳輸參數(孔隙率和滲透率等)，影響MPL的傳輸特性，進而影響PEM燃料電池的性能[6-7].因此，了解MPL傳輸參數與孔隙結構的關系是認識MPL傳質機制的關鍵，而孔隙尺度研究是其中最有效的一種研究方法.

多孔介質孔隙尺度模擬研究需要從介觀和微觀角度來構造孔隙結構并建立數學模型.Fazeli 等[8]提出了1種混合網絡模型計算GDL和MPL的有效擴散系數.用1種非重疊區域分解方法，即Dirichlet/Robin迭代子區域方法來處理GDL和MPL界面上的不連續液體飽和度[9].此外，格子玻爾茲曼方法(LBM) 也廣泛應用于MPL的研究[10-11].Kim等[10]采用兩相LBM研究了MPL和GDL中液態水的動態傳輸過程.結果表明，增加MPL厚度可以降低GDL中液態水含量，減少水達到穩態分布所需的時間.Zhang 等[11]采用LBM研究了GDL中水的傳輸和氧氣的擴散過程，并在二維空間中探究了MPL對燃料電池性能的影響，表明MPL的存在會降低多孔電極中的水含量，提高電流密度.Chen 等[12]應用二維LBM研究了宏觀孔隙及其分布對多孔電極中擴散組分傳輸的影響.結果表明，較多的大孔有助于傳質，但同時會降低有效反應面積.當忽略電化學反應時，MPL中氣體的傳輸過程與CL中類似.文獻[13]應用三維LBM研究了氧氣在CL中的擴散過程.結果表明，微孔結構的差異對有效擴散率的影響很顯著.不過，大多數的LBM方法在模擬GDL、MPL或CL內的傳輸過程時都采用了Bhatnagar-Gross-Krook(BGK) 單松弛時間(SRT)模型.SRT碰撞模型在處理多孔介質內部流動問題時具有數值不穩定和黏度依賴性的缺點[14].為了解決這些問題，學者們提出了多松弛時間(MRT)模型[15-17]，其中不同的松弛時間被用于不同的動力學過程.

目前，國內外學者對MPL的研究主要集中于采用不同的制備方法來尋找最優的MPL結構，實現優化PEM燃料電池性能的目的，然而對其內部傳輸機理的研究較少.部分模擬研究雖然探討了MPL微觀尺度下的傳輸過程，但有關不同孔隙結構對傳輸過程影響的研究還比較欠缺.本文使用改進的模擬退火(SA)方法[18]重建了MPL的孔隙結構，應用MRT/LBM方法模擬了MPL三維微孔隙內的流動過程，并研究了PTFE載量和PTFE的分布形貌對MPL孔隙率和滲透率的影響.

1 微擴散層重建

三維多孔介質重建方法可以分為兩大類：三維成像重建和虛擬隨機重建[18-29].前者利用從X射線或掃描電子顯微鏡獲得的多孔介質孔隙圖像來實現孔隙結構的數字化重建.后者基于實際多孔介質的統計信息來模擬孔隙結構的重建.與三維成像重建方法相比，虛擬隨機重建方法不受成像設備分辨率的影響，且成本更低，更容易實現[30].本研究采用了由Kim等[18]提出的基于球體的SA方法模擬重建了MPL，并與Stephenson等[31]提出的動態顆粒堆積(DPP)模型進行了對比.

MPL由3相組成：團聚的碳黑顆粒、PTFE和孔.由于碳黑顆粒的分布隨機，為簡化起見，重建過程做了以下假設：① 團聚的碳黑顆粒為均勻碳球形狀(掃描電鏡顯示MPL中碳相分布形態為類球形，因此本文假設碳黑顆粒為均勻碳球形狀)；② 允許少量碳球重疊(碳黑顆粒有團聚效應，本文用碳球重疊來類比此效應)；③ 忽略團聚的碳黑顆粒內部極小孔隙的影響(流體進入團聚的碳黑顆粒內部極小孔隙所受阻力很大，即只有極少氣體占比存在于其中，因此忽略其影響).在相同MPL尺寸(3個維度方向尺寸均為L個格子，即L×L×L個格子)、顆粒直徑d、孔隙率εP條件下，分別采用了SA和DPP兩種方法進行結構重建.

表1列出了基于球體的SA方法重建MPL結構的主要模擬參數.μ為控制碳球重疊程度的常數；參數λ控制溫度的下降速率；eSA為模擬退火算法的可接受相對誤差.lu、ts、mu分別對應LBM計算中長度、時間及速度的格子單位.

表1 基于球體的SA方法重建MPL的主要參數

1.1 基于球體的模擬退火方法

定義多孔介質的相指示函數

(1)

式中：j為相指示變量；x為坐標點.j相的體積分數可以通過Ij的平均值來計算：

εj(x)=〈Ij(x)〉

(2)

多孔介質的孔隙特性可通過兩點相關函數描述[18]：

S2,ij(x1,x2)=〈Ii(x1)Ij(x2)〉

(3)

式中：i為相指示變量.各向同性時，兩點相關函數只與兩點間距離r有關，即

S2,ij(r)=S2,ij(x,x+r)=〈Ii(x)Ij(x+r)〉

(4)

定義碳球顆粒的重疊概率為[18]

(5)

式中：V為碳球重疊部分與單個碳球的體積比.

在重建過程中，首先隨機布置碳球的初始分布，使碳球的個數滿足設定的碳球體積分數.初始化完成后，操作碳球在模擬域中隨機移動dx距離，隨機運動的規則概率函數[18]為

(6)

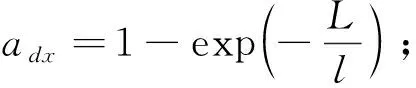
(7)

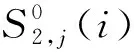
(8)

式中：

(9)

式中：H為Heaviside函數.

在碳球隨機移動過程中，判斷所選碳球移動與否的概率[18]為

(10)

式中：T為模擬退火溫度.T的變化速率控制著模擬過程的收斂速率，應在避免陷入局部能值最小態的前提下，盡可能地加快收斂速度.本文設置初始有效相交換概率為0.5，從而得到初始模擬退火溫度T0.模擬過程中T的變化規律為

Tn+1=λTn

(11)

式中：n為相應的迭代步數.

兩點相關函數的算法是影響計算效率的關鍵步驟.為減少計算量，在三維尺寸為L×L×L個格子的立方結構中兩點相關函數計算方法如下[18]：

(12)

式中：S2,jy,kz為ix方向上(此處用ix，jy，kz分別表示3個方向坐標軸)的兩點相關函數，其計算方法為

S2,jy,kz(l)=

(13)

式中：Nl為距離為l的樣本點個數.S2,kz,ix和S2,ix,jy也按相同的規則計算.

每一次有效相交換后，指示函數更新如下：

(14)

式中：Ijy,kz(ix)=I(ix,jy,kz)；Mm為間距為m的點個數；I′為每一次有效相交換前后指示函數的變化量；Δ為狄拉克函數.Δ的計算式為

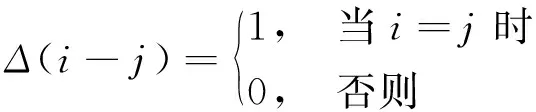
(15)

1.2 動態顆粒堆積模型

在DPP模型中，采用類似于分子動力學的方法來模擬顆粒的運動，其模擬尺度為介觀尺度而不是原子尺度.碳球顆粒間的相互作用采用Lennard-Jones相互作用勢能描述[31]：

(16)

交叉作用由下式給出：

(17)

只涉及碳相和孔相時，式(16)變為

(18)

采用DPP方法構建的MPL尺寸、格子長度和顆粒直徑與上述SA方法一致.DPP模型的參數是滿足物理特性的擬合值，本文中所使用的模擬參數為：Γii=0.8d，σii=0.8d，r=2d，并使用LAMMPS軟件模擬.

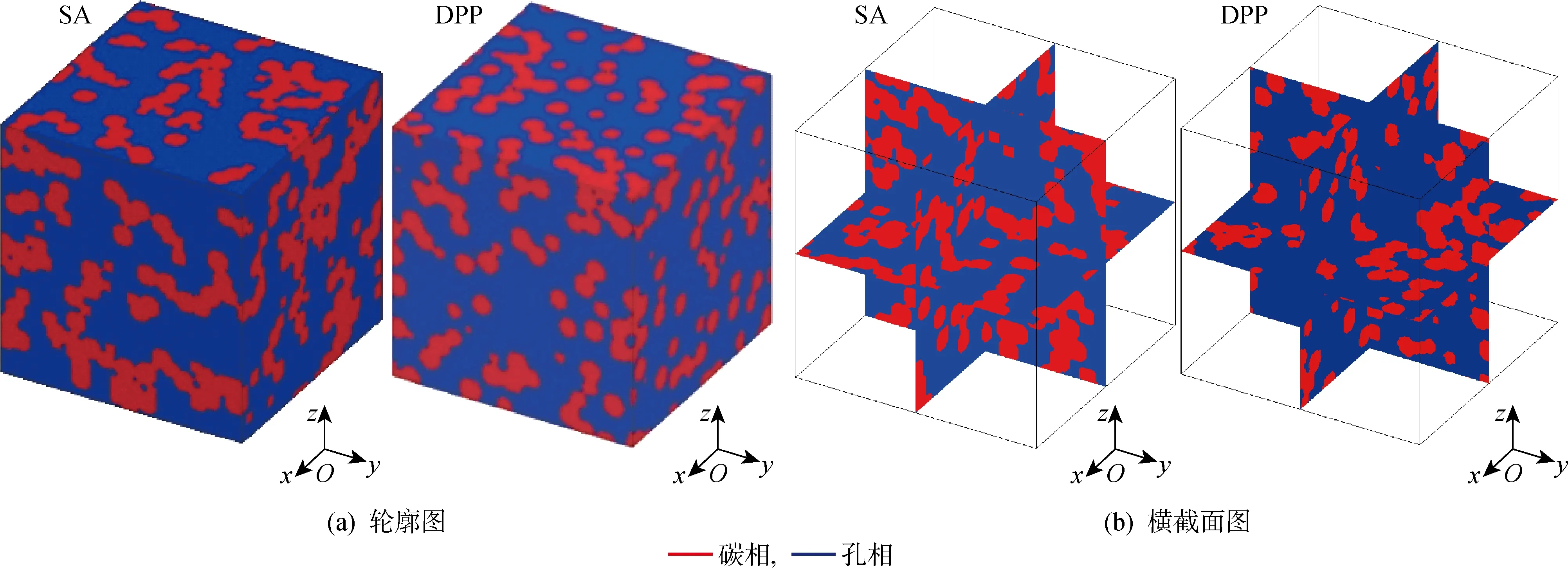
圖1 基于球體的SA方法和DPP模型重建的MPL中碳相和孔相結構Fig.1 Carbon and pore phase structures in MPL reconstructed based on sphere SA method and DPP model

1.3 孔徑分布

在實驗研究中，多孔介質的孔徑分布可以采用多種方法測量，如氣體吸收測量法、排液測量法和壓汞測量法[32-33].本文采用了Schulz等[34]提出的數值方法計算了重建后MPL中的孔徑分布.該方法包括兩個步驟：①沿著孔相與非孔相界面，生成半徑為rp的球體，球心位于界面處，球體中包含的區域設為非孔相.隨著該過程的進行，新的孔相與非孔相界面被重新定義.②沿著新的孔相與非孔相界面，再次生成半徑為rp的球體，球心位于新界面處，球體中包含的區域設為孔相.通過這兩個步驟，孔徑小于2rp的孔隙被剔除，余下的孔相被孔徑大于2rp的球體所占體積.逐漸增加rp重復兩個步驟，得到重建MPL中的孔徑分布.

1.4 兩種重建方法的比較

在基于球體的SA方法中，重建算法的目的是尋找滿足真實多孔介質某些統計特性的結構.文獻[35]對比了使用高階相關函數重建的多孔介質結構與僅使用兩點相關函數重建的結構，發現兩者傳輸特性差別不大，因此，兩點相關函數在表征多孔介質孔隙結構的應用中有著重要地位.SA算法和DPP模型都受到從多孔介質中提取的統計信息準確度的影響，而基于球體的SA算法在重建過程中比DPP模型有更多的約束條件.對于前者，存在3種限制：孔隙率、碳球重疊規則及兩點相關函數.對于后者，存在2種限制：孔隙率和Lennard-Jones相互作用勢能.圖1所示為采用SA方法和DPP模型重建的孔隙率為0.6的MPL中碳相和孔相輪廓圖以及中心橫截面上的相分布圖.可以看出，采用DPP模型構建的MPL中碳球顆粒的分散度更大，這是由于DPP模型是通過調整粒子間相互作用勢來間接比擬碳球重疊規則，進而滿足相應的孔隙率，而采用基于球體的SA方法構建的MPL滿足更多的結構信息，因此碳球的網絡連通度比較好.

圖2和圖3分別對比了兩種建模方法所得MPL多孔結構的孔徑分布和兩點相關函數，圖中D為孔徑，δ為孔徑分布.可以看出，相較于DPP模型，SA方法生成的MPL孔徑略大，這也證實了SA方法構建的MPL中碳球分布更為緊湊.對比兩者的兩點相關函數可知，重建過程結束時，SA方法所得結構的兩點相關函數與目標函數一致，而DPP模型所得結構與目標函數有差別.因此，采用SA方法比DPP模型更能反應MPL的孔隙連通信息.下文中，所有MPL孔隙結構都采用基于球體的SA方法重建.

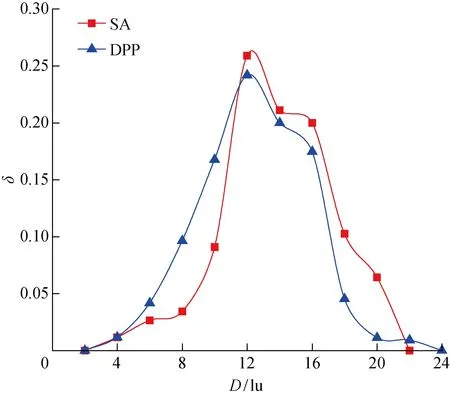
圖2 孔徑分布對比Fig.2 Comparison of pore size distributions

圖3 兩點相關函數對比Fig.3 Comparison of two-point correlation functions

1.5 MPL中PTFE分布的重建

MPL中需要添加PTFE來改善微孔隙的疏水性能，但PTFE也增加了孔隙結構的復雜性.一般而言，較高的PTFE含量會使MPL的疏水性更強，有利于水管理，但同時也會使孔隙率降低，增大傳質阻力，因此存在最佳的PTFE含量使得MPL的綜合性能最好[3].此外，相較于團聚的碳黑顆粒的內部孔隙，PTFE的顆粒更大，很難進入團聚顆粒的內部，主要分布在團聚顆粒之間的孔隙內[6].PTFE的分布狀態是隨機的，所以對于已得到的碳球結構，使用兩種方法來重建PTFE的分布.一種是將PTFE作為覆蓋在碳球顆粒表面的膜進行處理；另一種是根據孔隙格點周圍固體相的分布情況來選擇添加PTFE.PTFE的填充規律可以設定為孔隙格點周圍碳相和PTFE相越多，被PTFE填充的概率越大，即PTFE主要以塊的形式存在于碳相顆粒的結合處.兩種方法分別體現了PTFE在MPL內的兩種主要分布形貌，考慮MPL制備時PTFE可能存在的兩種分布形式，將這兩種方法分別標記為A方法和B方法.對于A方法，進一步考查了PTFE膜厚度分布的影響，假設PTFE膜為0～1個格子厚度隨機分布的A1方式和PTFE膜為0～2個格子厚度隨機分布的A2方式.對于B方法，考慮了局部隨機點填充更新PTFE的B1方式和統計完整區域相分布后填充更新PTFE的B2方式.A1與A2以及B1與B2的區別均包含了由于PTFE選擇分布的隨機性帶來的結構差異.顯然，將PTFE作為膜處理的A方法同時影響大孔和小孔，而根據格子點周圍不同相的分布隨機添加PTFE的B方法會優先影響小孔，后者的分布方式使多孔介質中非孔相連接更加緊密.

圖4所示為εP=0.5時，使用不同的PTFE重建方法得到的MPL的輪廓圖，對應的碳球體積分數為44.1%，PTFE體積分數為5.9%，PTFE與碳相的質量比(亦稱PTFE載量)w(PTFE)/w(C)為0.15.可以看出，在相同孔隙率下，4種處理方式PTFE的分布雖略有不同，但差別比較小，尤其是B1和B2方法所生成的結構差別更小.圖5給出了圖4所示結構的孔徑分布.可以看出，εP=0.5時，A和B兩種PTFE重建方法會影響MPL的孔徑分布，但A1、A2、B1及B2四種方式對重建后的孔徑分布幾乎沒有影響.因此，PTFE膜的厚度分布對MPL孔隙分布的影響很小，考慮局部相分布的方式與考慮整體區域相分布的方式相比也幾乎沒有區別，而B1方法的重建效率更高.在本文有關 PTFE 分布對MPL孔隙結構以及滲透率影響的研究中均使用A1和B1方式構建了PTFE在MPL中的分布，并對兩種重建方式對MPL孔隙結構的影響做了對比.

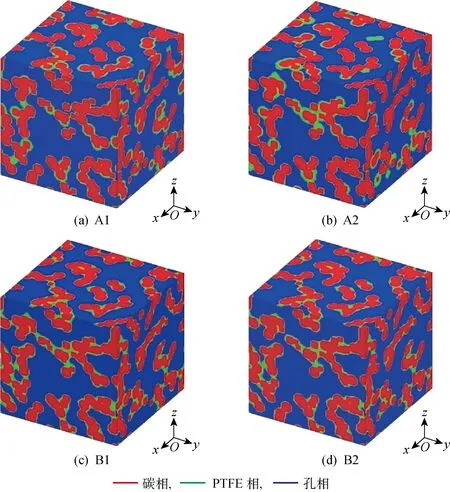
圖4 w(PTFE)/w(C)= 0.15、εP= 0.5時，不同PTFE重建方法得到的MPL輪廓圖Fig.4 MPL contour maps obtained by different PTFE reconstruction methods at w(PTFE)/w(C)=0.15 and εP=0.5

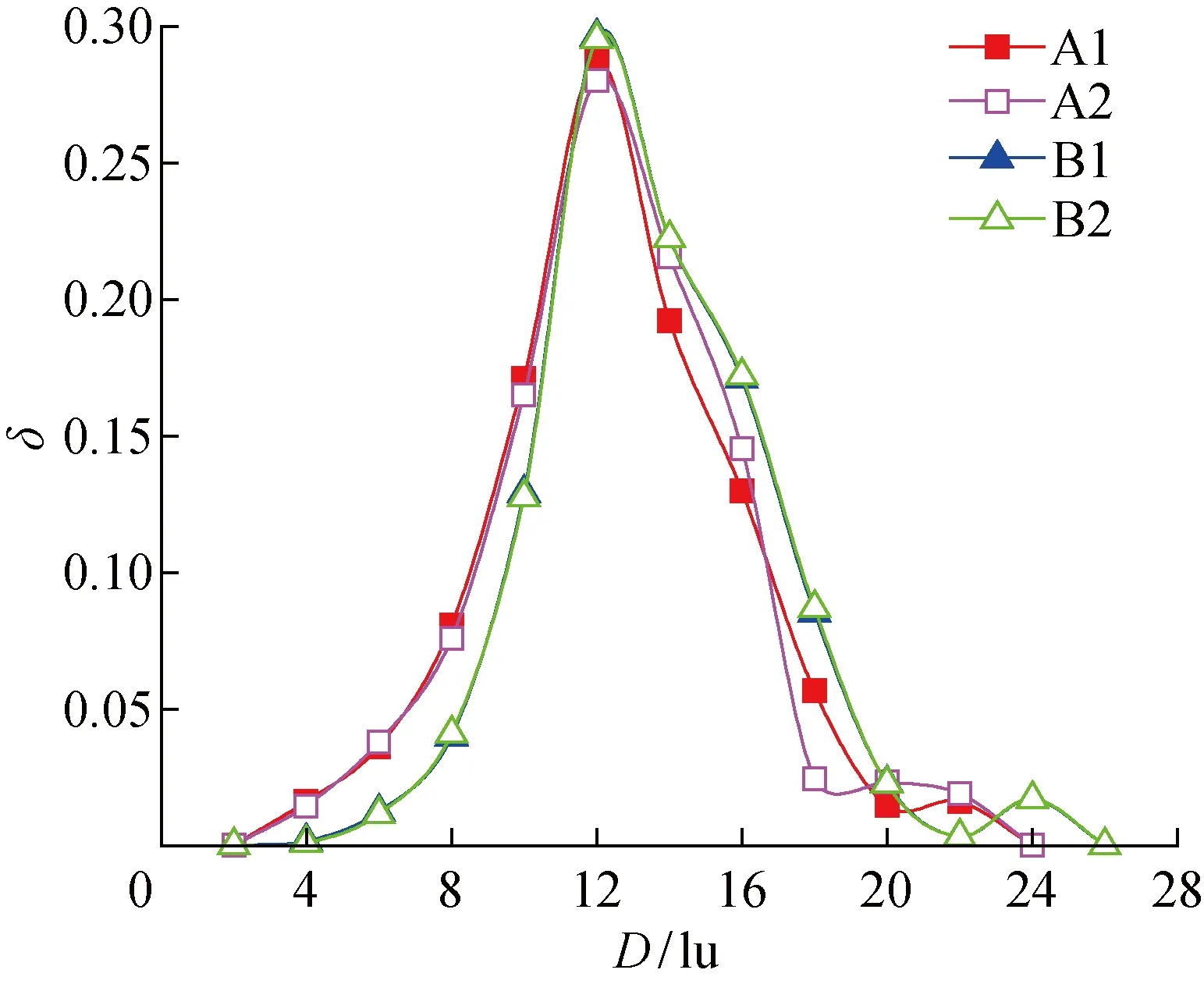
圖5 w(PTFE)/w(C)= 0.15、εP= 0.5時不同PTFE重建方式得到的MPL的孔徑分布Fig.5 Pore size distribution of MPL obtained by using different PTFE reconstruction methods at w(PTFE)/w(C)= 0.15 and εP= 0.5

2 孔隙尺度模擬方法

本文采用單相多松弛時間格子玻爾茲曼方法模擬了重構的MPL內的流動過程.MRT/LBM模型由SRT/LBM模型發展而來，通過變換矩陣將速度分布函數轉換為矩空間分布函數.在矩空間根據相應物理過程的不同時間尺度以不同的松弛時間執行松弛碰撞過程，有關MRT/LBM方法的詳細信息參見文獻[36].模型中采用了多反射(MR)邊界條件[36]處理流固界面，并通過體積力驅動流體流動，其主要模擬參數如表2所示.

表2 孔隙尺度模擬的主要參數Tab.2 Main parameters of pore scale simulation

為了驗證本模型，分別模擬了簡單立方球堆積、體心立方球堆積和面心立方球堆積多孔介質內的流動，并通過達西定律計算了多孔介質的絕對滲透率[36-40]：

(19)

式中：u為多孔介質內流體的表觀速度；k為滲透率；ρ為流體密度；p為壓力.

另外，Kozeny-Carman(KC)關系式是被廣泛使用的關于多孔介質滲透系數的半經驗公式，其形式為[41]

(20)

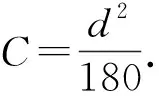
圖6所示為k/d2(即無量綱滲透率)的LBM模擬值、Zick和Homsy的理論值[42]以及KC關系式計算結果的對比結果.可以看出，LBM模擬得到的滲透率隨孔隙率的變化曲線與理論值非常吻合，而由于KC關系式是在較小孔隙率時測量密集球堆積得到的半經驗公式，所以隨著εp增加，KC關系式的預測結果與理論值的偏差逐漸增大.

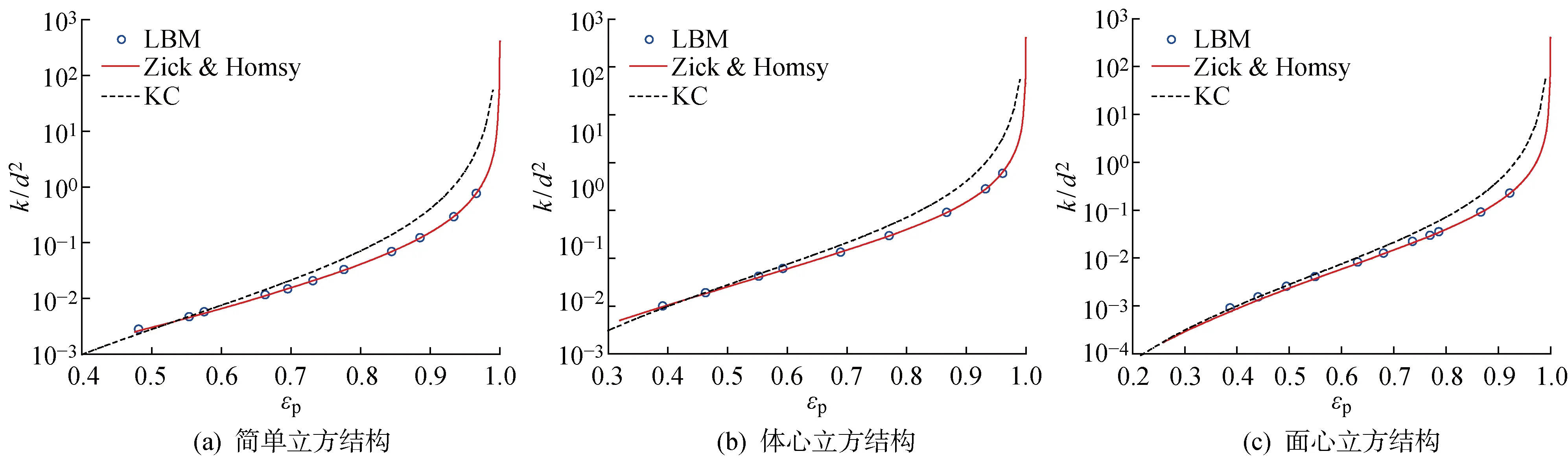
圖6 k/d2的LBM模擬值、Zick和Homsy的理論值[42]以及KC關系式計算結果的對比Fig.6 Comparisons of k/d2 of the LBM simulation value, Zick and Homsy’s theoretical value [42] and the calculation results of KC formula

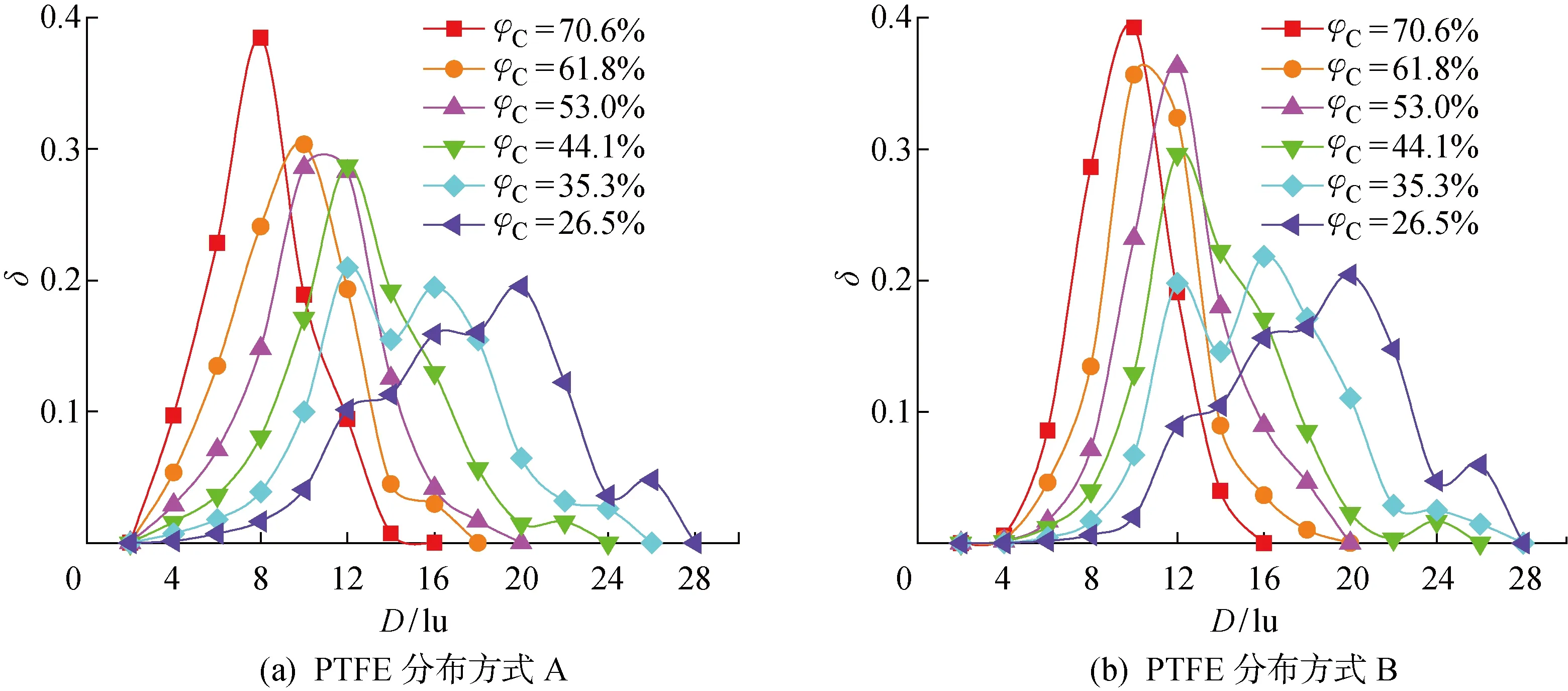
圖7 w(PTFE)/w(C)= 0.15時MPL孔徑分布隨碳相體積分數的變化Fig.7 Changes of pore size distribution of MPL reconstructed with volume fraction of carbon at w(PTFE)/w(C)= 0.15

3 模擬結果與分析

3.1 碳球體積分數對MPL孔隙結構和滲透率的影響

Park等[43]的研究表明，MPL中PTFE的質量分數在15%附近時，PEM燃料電池的性能最優.首先假設PTFE的含量保持在這一最優值附近，取w(PTFE)/w(C)=0.15，探究了PTFE在A和B兩種分布形貌時MPL的孔隙結構和滲透系數與碳相體積分數φC之間的關系.

圖7和圖8分別為碳相體積分數變化時，A和B兩種PTFE分布形貌時MPL的孔徑分布及其平均孔徑D′的變化.從圖中可以看出，隨著碳相體積分數的減小，孔相占比增大，孔徑分布曲線右移，對應的平均孔徑也逐漸增大.從圖7也可以明顯看出，φC約為44.1% (孔隙率約為0.5)時，MPL的孔徑分布有明顯的差異.φC>44.1%時，孔徑分布表現為典型的單峰值曲線，峰值孔徑所占比例較大；而φC<44.1%時，在22～26 lu大孔徑區出現第二峰值的趨勢越來越明顯，而且孔徑分布的范圍也變大.圖8也顯示，平均孔徑隨碳相體積分數的減小而增加的程度在φC為44.1%時增大.

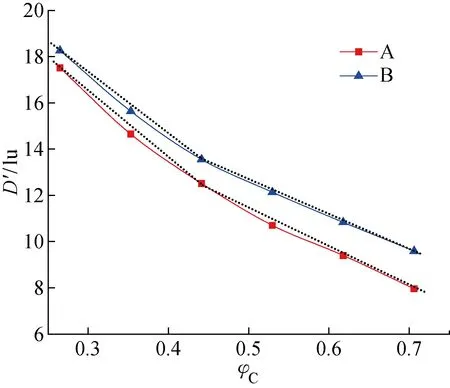
圖8 平均孔徑隨碳相體積分數的變化Fig.8 Changes of average pore size with volume fraction of carbon

圖9所示為φC=61.8%、φC=44.1%時，A和B兩種PTFE分布形貌的MPL孔徑分布.PTFE以膜方式附著在碳顆粒表面，與PTFE主要存在于碳球結合處相比，MPL內的孔隙尺寸偏小，尤其是孔隙率較小時此特性更加明顯，這也進一步驗證了上文提到的PTFE以B方式分布較A方式能使MPL的非孔相更加緊密.

圖10為w(PTFE)/w(C)= 0.15時，PTFE 在A和B兩種分布形貌的MPL無量綱滲透率與碳相體積分數的關系.從圖中可以看出，由于B分布方式生成的結構孔徑更大，而大孔徑有助于流動和傳質，所以MPL中PTFE以B分布方式存在時得到的滲透率比A分布方式略大，并且兩種分布方式所得滲透率的差別在孔隙率較大時更加顯著，這也與圖7～9中的孔徑分布變化顯示的規律一致.

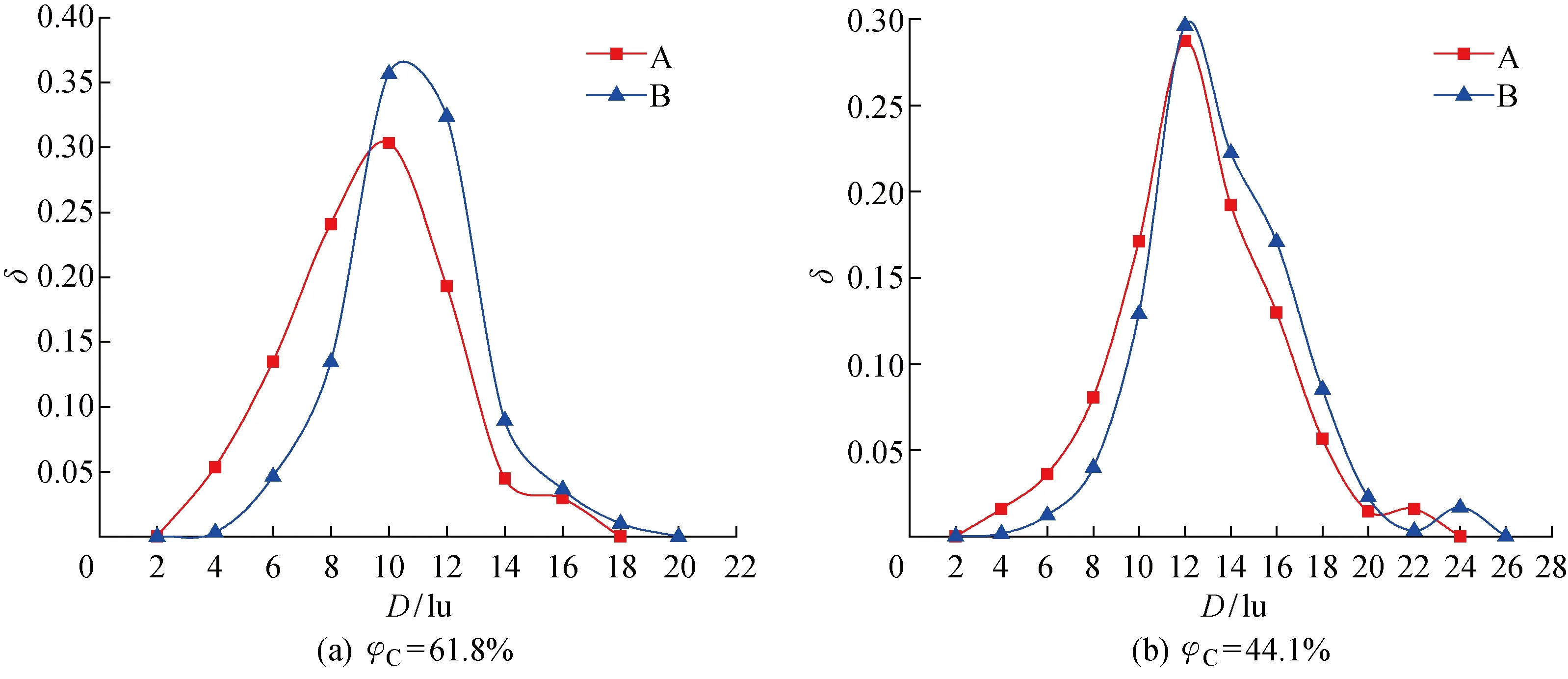
圖9 w(PTFE)/w(C)= 0.15時MPL的孔徑分布Fig.9 Pore size distribution of MPL reconstructed at w(PTFE)/w(C)= 0.15

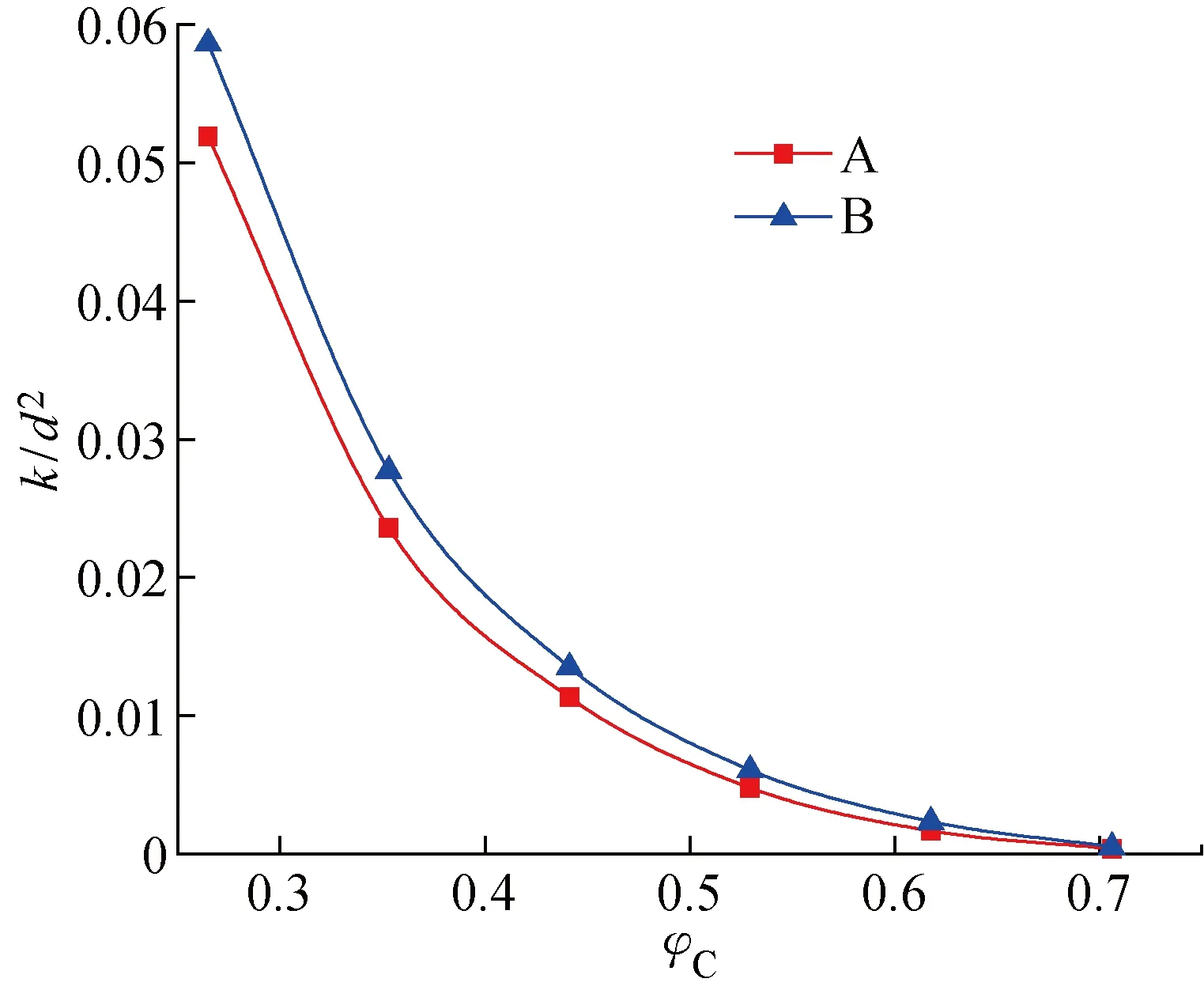
圖10 w(PTFE)/w(C)= 0.15時MPL的無量綱滲透率與碳相體積分數的關系Fig.10 Dimensionless permeability of MPL versus volume fraction of carbon at w(PTFE)/w(C)= 0.15

3.2 PTFE載量對MPL孔隙結構和滲透率的影響

MPL在疏水處理時使用的PTFE會填充MPL結構中的孔隙，從而黏合碳球形成比較固定的多孔框架.因此，PTFE的載量會對MPL的微結構產生重要的影響.本節探究PTFE載量對MPL孔隙結構及滲透率的影響.假設碳相體積分數為50%，且模擬域和碳顆粒的尺寸與上文一致.

圖11為w(PTFE)/w(C)在0～0.4時MPL的孔徑分布圖.可以看出，隨著w(PTFE)/w(C)的增加，A方式中更多的碳球表面被PTFE覆蓋，幾乎所有孔隙的大小均受到影響，孔隙分布向左側移動；而B方式孔徑分布曲線移動的趨勢不明顯，僅小孔徑區受w(PTFE)/w(C)增加的影響更大.圖12對比了w(PTFE)/w(C)為0.1和0.4時，A和B兩種PTFE分布形貌時MPL的孔徑分布.可以看出,w(PTFE)/w(C)較大時， PTFE的分布形貌對孔隙分布的影響更大.圖13所示為對應的平均孔徑隨w(PTFE)/w(C)的變化.可以看出，由于PTFE以B方式分布時會優先影響小孔，在PTFE含量較少時平均孔隙隨w(PTFE)/w(C)的增加有少許增大.隨著PTFE含量的進一步增大，更多的孔隙將被填充，被PTFE填充的大孔占比增多，平均孔隙也隨之減小.而PTFE以 A方式分布時，由于其對大孔和小孔的影響程度相同，平均孔隙大小隨w(PTFE)/w(C)的增加逐漸降低，這與B方式有略微的差異.圖14為碳相體積分數0.5時，PTFE在A和B兩種分布形貌下，MPL無量綱滲透率與w(PTFE)/w(C)之間的關系.可以看出，MPL的滲透率明顯受到w(PTFE)/w(C)和PTFE分布的影響，而且PTFE以A方式分布時，對大孔的影響較B方式更明顯，滲透率受w(PTFE)/w(C)的影響也更大.雖然在PTFE含量較少時，B方式下MPL的平均孔徑隨w(PTFE)/w(C)的增加而略有增大，但由于孔隙率減小，滲透率因此也減小.

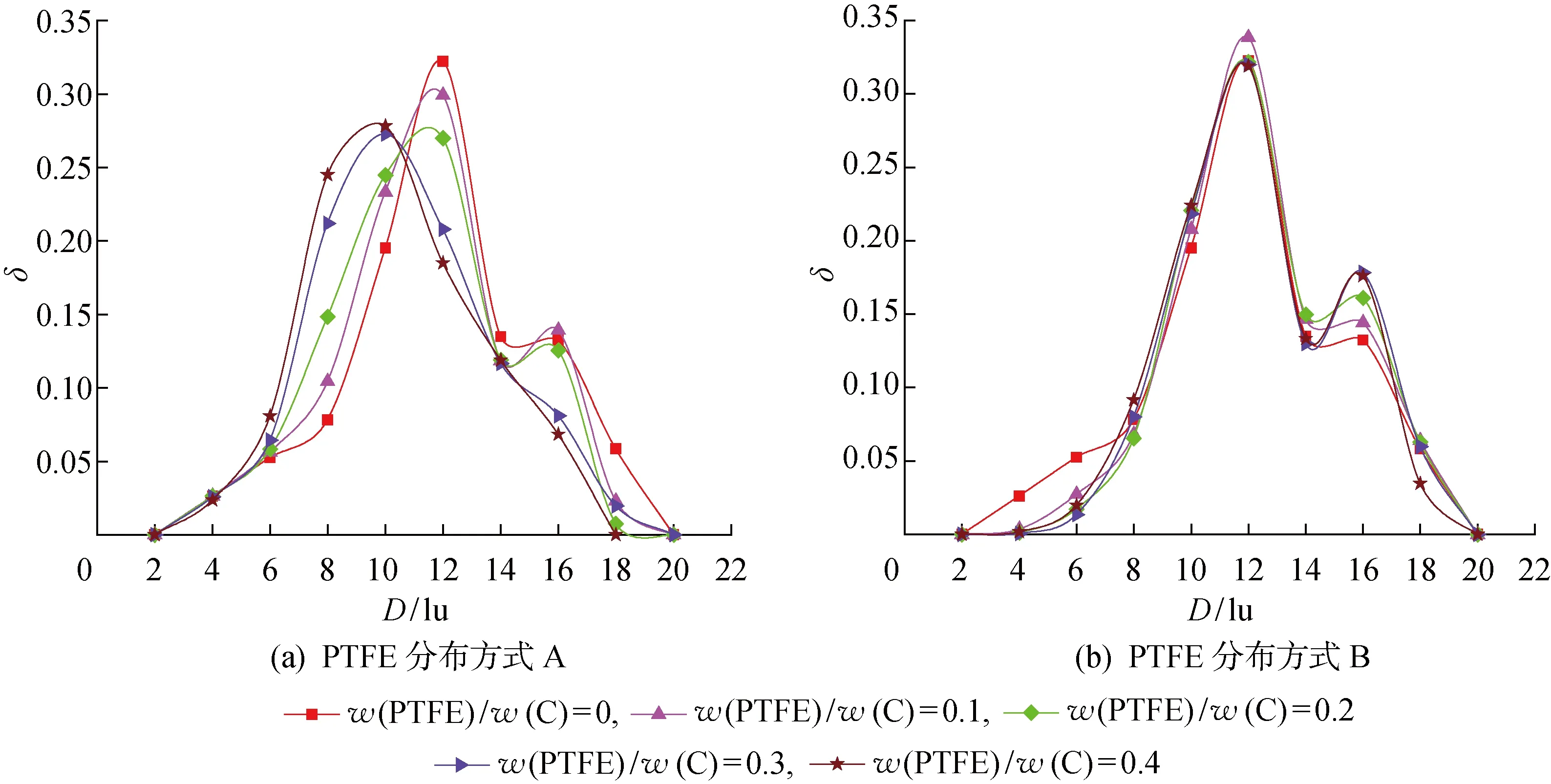
圖11 φC=0.5時MPL的孔徑分布隨PTFE載量的變化Fig.11 Pore size distribution of MPL reconstructed at different PTFE levels while φC=0.5

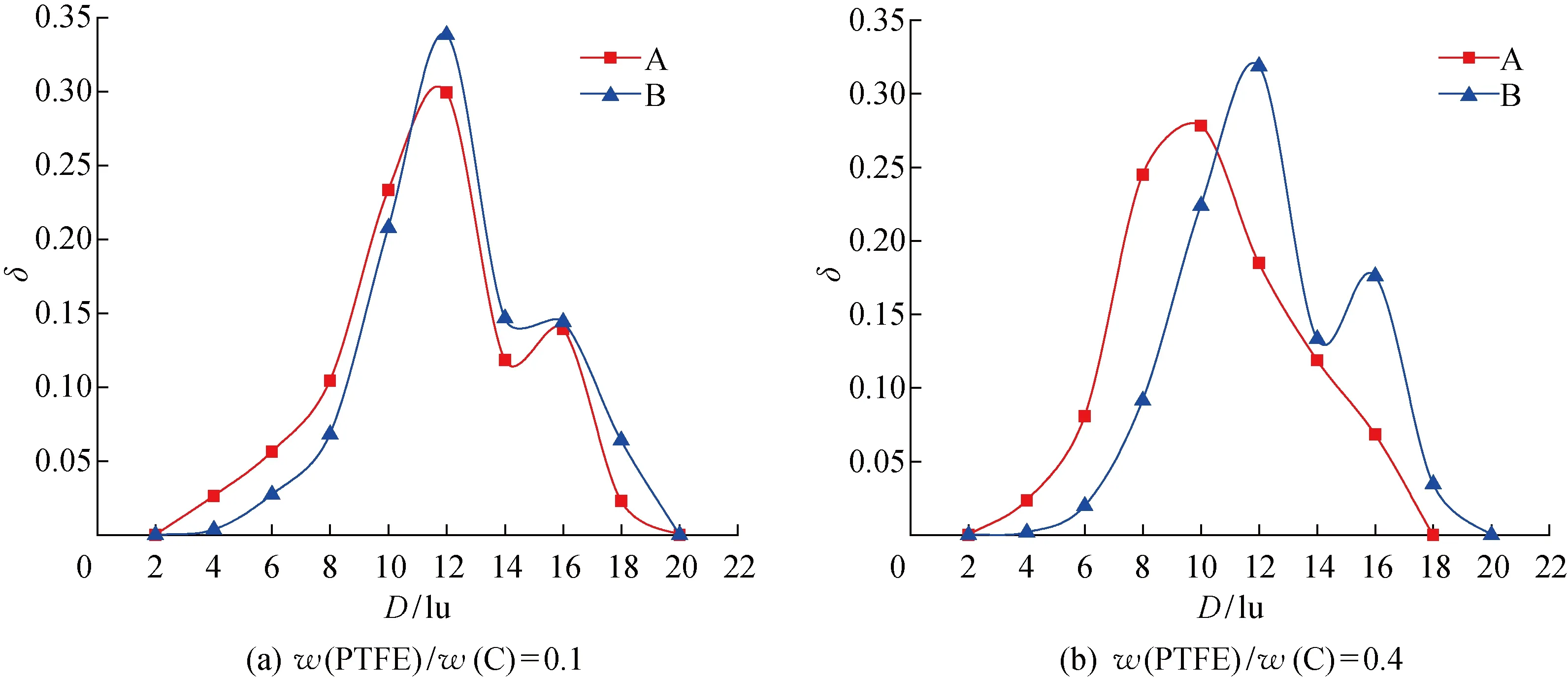
圖12 φC=0.5時不同PTFE分布形貌的MPL孔徑分布Fig.12 Pore size distribution of MPL reconstructed at φC=0.5

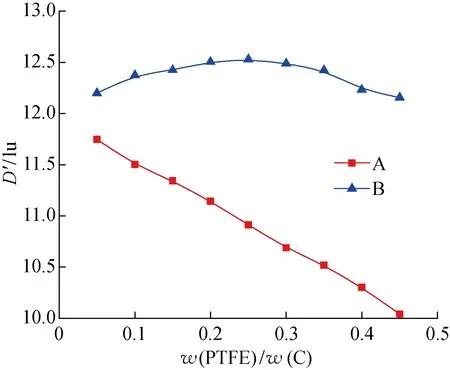
圖13 平均孔徑大小隨PTFE載量的變化Fig.13 Average pore size versus load of PTFE

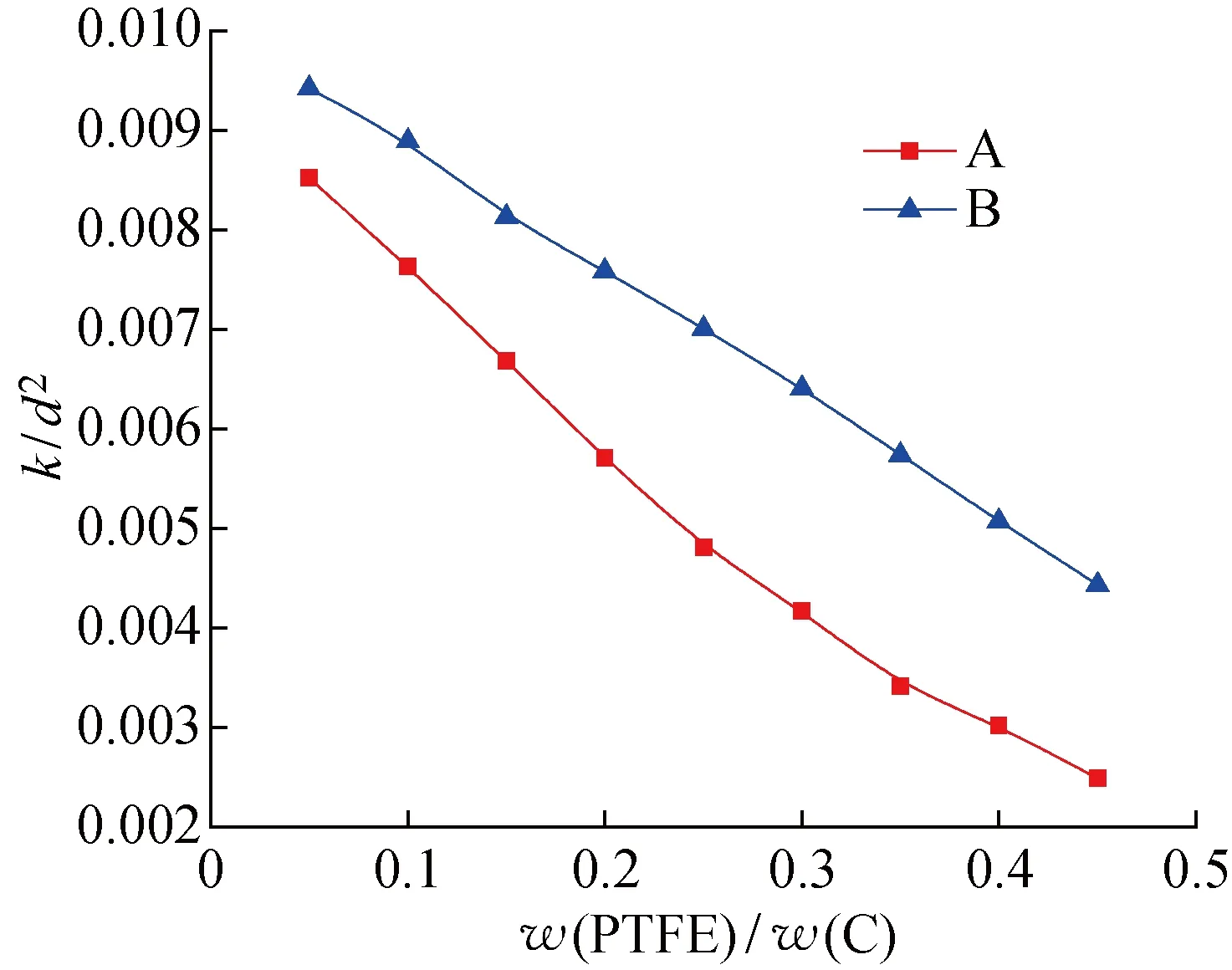
圖14 φC=0.5時PTFE不同分布形貌的MPL的無量綱滲透率與PTFE載量的關系Fig.14 Dimensionless permeability of MPL reconstructed versus load of PTFE

3.3 MPL滲透率與孔隙率的關系

將碳相體積分數以及PTFE載量轉換為MPL的孔隙率，得到無量綱滲透率與孔隙率的關系，如圖15所示.可以看出，無量綱滲透率隨孔隙率的增加而增大，并且PTFE以B方式分布所得滲透率大于同參數下的A方式分布.式(20)的預測值低估了MPL的滲透率，而且通過擬合KC關系式的KC常數也無法得到很好的擬合結果，因此本文提出了如下關聯式來擬合本文得到的MPL滲透率：

(21)

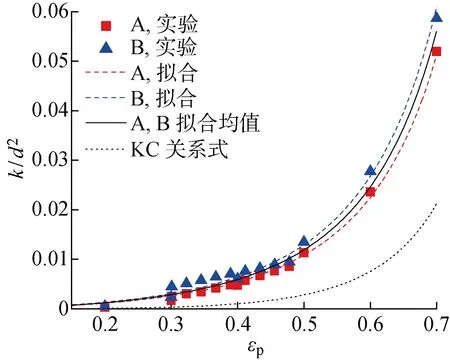
圖15 MPL無量綱滲透率隨孔隙率變化Fig.15 Dimensionless permeability of MPL versus porosity

式中：a和b是擬合參數.本文研究發現，a=1.43和b=2.1可以很好地擬合出PTFE在A和B兩種分布形貌時MPL的滲透率.對于A分布形貌，C=0.006 8.對于B分布形貌C=0.008 1，即MPL中PTFE以B方式分布時的滲透率比A分布形貌約大20%.考慮到在實際的MPL中，PTFE 的兩種分布形式都可能存在，如果取C的平均值 0.007 45，式(21)預測得到的MPL滲透系數在孔隙率0.3～0.6與孔隙尺度模擬計算結果的相對誤差不超過12%.另外，碳球顆粒直徑的取值對計算MPL的絕對滲透系數影響很大.對于標準的碳黑顆粒，其直徑大約為50 nm.若不考慮碳黑顆粒的團聚，計算得到MPL的絕對滲透系數在孔隙率0.3～0.6范圍內為1.0×10-17～7.0×10-17m2，這些值大約比實驗測量值低3個量級[24,44].實際中，MPL的縫隙可能會對滲透系數的測量產生很大的影響，而且碳黑顆粒也通常會以團聚的形式形成較大的碳球顆粒.如果取團聚碳黑顆粒的平均直徑為2～3 μm[24,44]，經計算，得到孔隙率為0.5時MPL的滲透系數為 6.0×10-14～1.3×10-13m2，接近實驗測量值.

4 結論

運用基于球體的模擬退火方法和動態顆粒堆積模型數值重建了燃料電池微擴散層，分析了碳相體積分數、PTFE載量以及PTFE的分布方式對重建的微擴散層孔隙結構的影響，并應用多松弛格子玻爾茲曼模型研究了微擴散層的滲透率.主要結論有：

(1) 相對于動態顆粒堆積模型，基于球體的模擬退火方法能更加準確地反應重建的微擴散層的孔隙信息；

(2) PTFE的分布方式影響微擴散層的孔隙結構和滲透率，當PTFE以膜的形式包覆在碳相表面時，微擴散層內的固相分布相對較松散，且孔隙尺寸和滲透系數都較小；

(3) 隨著碳相體積分數的增加，微擴散層的孔隙尺寸和滲透率減小，但在碳相體積分數大于44.1%后，微擴散層孔隙尺寸減小的程度變小；

(4) 當 PTFE以塊的方式存在于碳相顆粒的結合處時，微擴散層的孔隙分布受PTFE載量的影響較小，但小孔數量隨著PTFE載量的增加而減小，而且在PTFE含量較少時微擴散層的平均孔隙尺寸隨PTFE載量的增加而增加；

(5) 計算得到的微擴散層的滲透率大于KC關系式的預測值，分析擬合結果確定了擬合參數，該公式考慮了碳相比例、PTFE載量及PTFE分布的綜合影響，預測結果在微擴散層孔隙率0.3～0.6范圍內與孔隙尺度模擬結果的相對誤差小于12%.