在動態幾何實驗教學中培養學生的數學直覺
王思敏 周松林 林宇杰
([1]廣西師范大學數學與統計學院 廣西·桂林 541004;[2]桂林市第一中學 廣西·桂林 541004)
數學直覺是對于數學對象事物(結構及其關系)的某種直接領悟或洞察。在傳統數學教學中,培養學生的數學直覺常常缺失“顯微鏡”和“放大鏡”等技術的支持。而動態數學技術具有數學化、視覺化、動態化呈現數學對象與思維的功能,應用動態數學技術是數學實驗教學中培養學生數學直覺的利器。本文嘗試探討在幾何實驗教學中利用動態數學技術培養學生數學直覺的一些思考。
1 在平面幾何實驗教學中,精準繪測,捕捉數學直覺
在傳統教學中,學生無法測量數學對象的長度、面積等數值,因此在平面幾何學習中易錯失許多“特殊”的數量關系,難以捕捉數學直覺。在基于動態數學軟件的實驗教學中,可以選擇“測量”功能,任意測量數學對象的數值,通過變化數值,指引學生捕捉數學直覺,助力學生直觀感知數據背后的規律。
案例一:從勾股定理到余弦定理。
勾股定理是最基本的幾何定理,在常規教學中,教師通過設計案例來引導學生發現這一定理。但若不通過預先設計好的案例,能否讓學生自己發現這一規律呢?從動態數形結合來看,利用動態數學技術測量和拖拽功能,有助于驗證勾股定理在任意三角形中都成立。借用這種數學直覺,不妨測量非直角三角形的邊長。
通過測量三角形多邊長度,如圖1,在△ABC中,AD⊥BC,觀察可得。為什么會出現這種情況呢?不難發現AB、BD分別是Rt△ABD的斜邊和直角邊;AC、DC分別是Rt△ADC的斜邊和直角邊,根據勾股定理有上述等式成立。
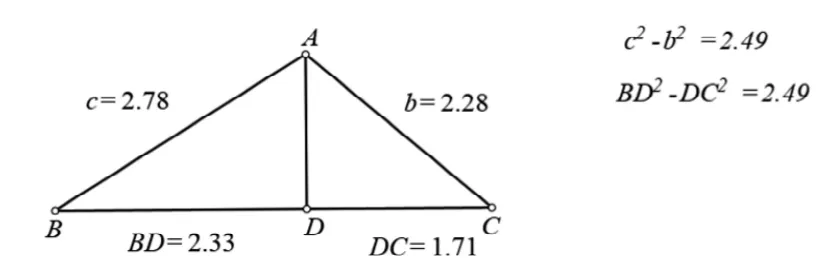
圖1

即證余弦定理。相較于傳統教學中用向量推導余弦定理的方法,此種推導方式顯示出其巧妙性:在實驗教學中,學生使用動態數學軟件測量功能發現等量關系藉此捕捉數學直覺“類似勾股定理”,將其轉化為△ABC三邊長的數量關系。再按平方差公式展開并用進行等量代換,最終實現余弦定理的推導。
2 多元表征立體幾何,激發數學直覺
教材中立體幾何的公理或定理大都直接給出,但很難讓人直觀感知或想象。在動態數學實驗教學中,可以任意切換三維與二維圖形,實現多視角觀察立體圖形的結構與構成要素;通過二維、三維圖象、動畫演示、顏色閃動、文字解說、語言互動等多元方式表征,一方面降低了空間想象上的負荷,另一方面也激發學生對學習對象的興趣,有助于實現“授人以魚的同時,更授人以漁與欲”。
案例二:從祖暅原理到空間幾何體的面積。
《九章算術》中提到祖暅在求球體積時,使用的原理是:“冪勢既同,則積不容異”。“冪”是截面積,“勢”是立體的高。意思是兩個同高的幾何體,如在等高處的截面積都相等,則它們的體積相等。祖暅原理可用于推導球的體積公式,類似于微元法分割。但這個原理以靜態的圖像演示相對困難,學生難以發現同一平面切面的圓環與圓的面積相同。
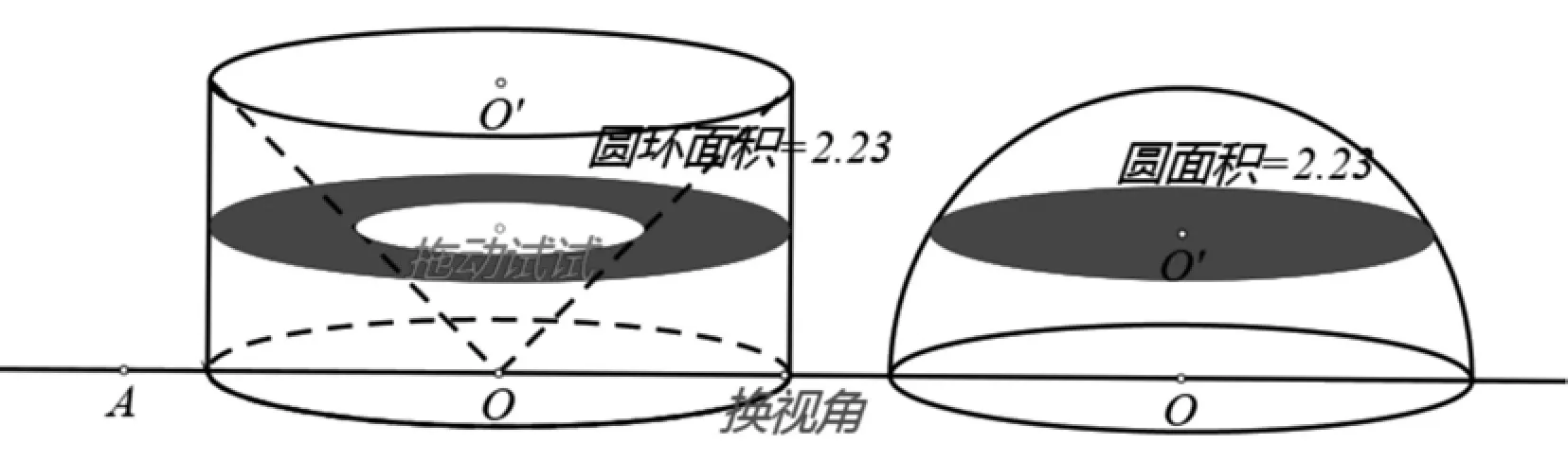
圖2

3 動態探究解析幾何,訓練數學直覺
解析幾何中的動態幾何問題是教學的重難點,傳統教學中的“化動為靜”方法將運動的動圖裁剪成單幀的靜態圖片,對學生的直觀感知能力要求較高。相比而言,動態數學實驗教學重現數學圖形運動過程,學生可以隨時按下暫停鍵觀察。這樣在學生腦海中便不是截斷的圖片,而是連貫的動圖,在動態中解決動態問題,相對符合學生的認知發展規律。
這是一道考查圓與拋物線位置關系的練習題,不難看出圓的圓心是(a,0),半徑恒為1。常規做法是將拋物線方程代入到圓的方程中,可以得到
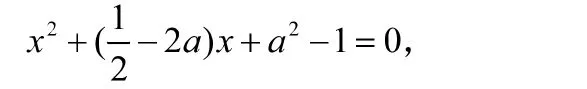
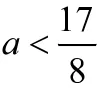
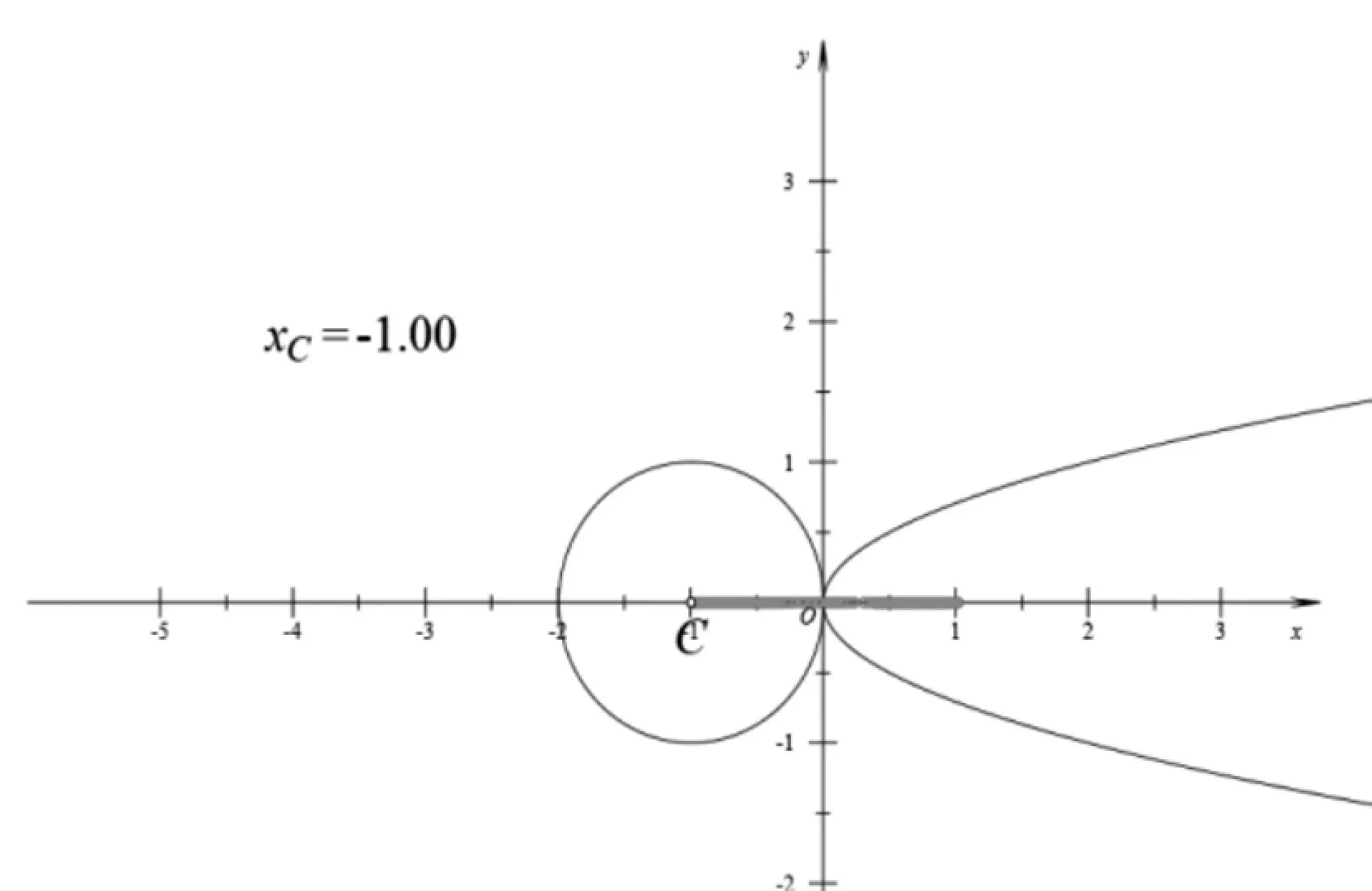
圖3
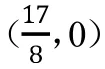
究其出錯緣由,學生在日常學習中過多依賴代數,缺乏數形結合的思想。沒有經過幾何直觀,便無法在腦海中形成清晰表象,也就無法解決由于認知偏差所帶來的失誤。動態數學軟件的作圖、測量、跟蹤等功能可以幫助學生理解圖形,建立圖形的數量關系,增強直觀想象能力。
4 結語
日本數學家小平邦彥說:“數學就是一種感覺”。動態數學技術在探索定理、證明命題、解題教學中的合理使用,能有效培養數學直覺。值得說明的是,即便動態數學實驗教學能夠測量并發現一些數學事實,但它不能代替邏輯推理的歸納演繹。在一定程度上,動態數學技術有助于發現和探索數學規律,培養數學直覺,但直覺作為一種非理性的思維,具有一定主觀性,需要辯證對待。

