關于折疊問題突破策略的舉例探究

季慧

[摘? 要] 圖形折疊是中考數學的難點問題，其中涉及眾多幾何特性和數學規律，在解析時需要采用合理的方法策略來構建思路.文章以2019年中考的折疊問題為例，探討折疊問題常用的四種突破策略，并提出相應的教學建議，與讀者交流.

[關鍵詞] 幾何折疊;折疊問題;全等;軸對稱

圖形折疊是初中數學的重點內容，以其為背景的折疊問題是中考的常見題型，該類問題常借助圖形折疊來考查軸對稱變換、幾何特性、三角形全等、解直三角形等知識，問題綜合性較強，解析時可以采用多種方法策略. 下面探究其解析策略，探討問題教學.

解析策略舉例探究

折疊問題的核心內容是軸對稱，其中的折疊特性也是基于該內容所構建的，而在探究解析時可以采用多種策略，如把握其中的變量與不變量、軸對稱的垂直平分關系、圖形折疊中的特殊關系與特殊位置等，充分挖掘問題中的隱含信息，構建相應的解題思路.

策略一：把握折疊中的變量與不變量

折疊是圖形動態變化的過程，在該過程中“變”的是位置，而“不變”的是圖形本身所具有的特性，因此在實際解析時可以把握其中的變量與不變量，根據不變量來提取恒定關系，打開解題突破口.

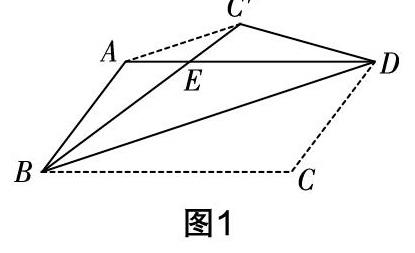
例1? （2019年江蘇省常州市中考卷）如圖1，把平行四邊形紙片ABCD沿BD折疊，點C落在點C′處，BC′與AD相交于點E.

（1）連接AC′，則AC′與BD的位置關系是____________;

（2）EB與ED相等嗎？證明你的結論.

分析? （1）題干給出了圖形折疊的過程，根據幾何性質和折疊特性可知AE=C′E，由三角形內角和定理可得等角關系，進而可推AC′與BD的平行關系;（2）初步分析EB與ED相等，對于該結論可以由等腰三角形的“等角對等邊”來獲得，因此可從幾何角來切入.

解? （1）連接AC′，由于AD=C′B，ED=EB，則AE=C′E，由三角形內角和定理可知∠EAC′=∠EC′A=∠EBD=∠EDB，所以AC′∥BD.

（2）根據折疊特性可知∠CBD=∠C′BD，由于AD∥BC，所以∠ADB=∠CBD，進而可推知∠EDB=∠EBD，則△BED為等腰三角形，有EB=ED.

策略二：活用軸對稱中的垂直平分

折疊前后的圖形關于折痕對稱，即折疊所形成的圖形為軸對稱圖形，由軸對稱特性“對稱軸垂直平分對應點的連線”可提取等長和垂直線段，由該特性可構建相等、垂直關系，有利于確定后續解析的方向.

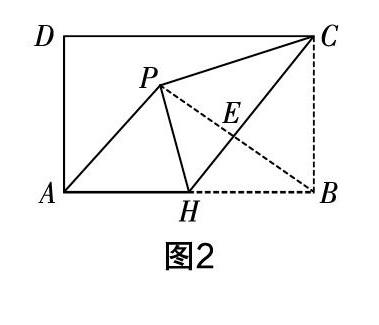
例2 （2019年江蘇省淮安市中考卷）如圖2所示，在矩形ABCD中，AB=3，BC=2，H是AB的中點，將△CBH沿CH折疊，點B落在矩形內點P處，連接AP，則tan∠HAP的值為______.

分析? 連接PB，交CH于E，根據軸對稱特性和三角形內角和定理可得CH垂直平分PB，同時可證PA∥CH，可得出∠BAP=∠BHE，可在Rt△BCH中構建∠HAP的正切關系，從而代入線段長求值.

解? 連接PB，與CH的交點設為點E，折疊前后的圖形關于折痕軸對稱，根據軸對稱特性可知點E為線段PB的中點，而線段PB⊥CH. 根據條件可推得AH=BH=PH，所以∠HAP=∠HPA，∠HBP=∠HPB，進而可知∠APB=90°. 由PB⊥CH可證PA∥CH，所以∠HAP=∠BHE. 在Rt△BCH中，已知BC=2，BH=■，則tan∠HAP=■=■，即tan∠HAP的值為■.

策略三：提取折疊圖形中的特殊關系

圖形折疊過程中必然涉及一些特殊的圖形和特殊關系，例如全等三角形、相似三角形、直角三角形等，根據其對應特性即可提取特殊關系，合理利用其中的特殊關系可以構建解析思路，簡化解題過程.

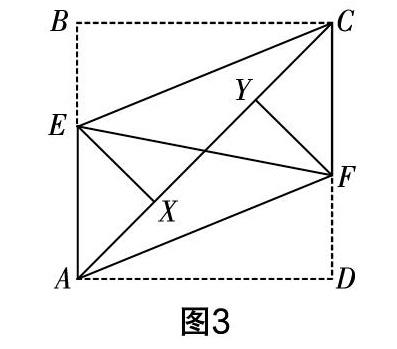
例3? （2019年廣東省深圳市中考卷）如圖3所示，在正方形ABCD中，BE=1，將BC沿CE翻折，使B點對應點剛好落在對角線AC上，將AD沿AF翻折，使D點對應點剛好落在對角線AC上，則EF的線段長為______.

分析? 過點F作AB的垂線，垂足為點M，根據折疊和等腰直角三角形的性質可知EX=EB=AX=1，∠EXC=∠B=90°，AM=DF=YF=1. 而由勾股定理可知AE=■，進而可推知正方形邊長AB的長，以及EM的長，后續利用勾股定理可求出EF的長.

解? 作FM⊥AB于點M，如圖4所示，已知四邊形ABCD為正方形，則有∠BAC=∠CAD=45°. 分析圖形折疊的過程，可知EX=EB=AX=1，∠EXC=∠B=90°. 在Rt△AEX中使用勾股定理可得AE=■=■. 點D的翻折落點是點Y，則AM=DF=YF=1，可推知正方形的邊長AB=FM=■+1，則EM=■-1. 在Rt△EMF中使用勾股定理可得EF=■=■，即EF的線段長為■.

策略四：討論折疊中的落點位置

在圖形折疊過程中落點是其較為重要的內容，折疊的落點不同所形成的復合圖形也具有較大差異，對于落點不明確的問題則可以對其加以討論，形成對應幾何模型，據此構建相應的解析思路.

例4? （2019年河南省中考卷）如圖5所示，在矩形ABCD中，AB=1，BC=a，點E在邊BC上，且BE=■a. 連接AE，將△ABE沿AE折疊，若點B的對應點B′落在矩形ABCD的邊上，則a的值為______.

分析? 本題目沒有明確點B的對應點B′的落點，需要分兩種情況加以討論：①點B′落在AD邊上，②點B′落在CD邊上. 針對不同的情形需要根據折疊特性及相關幾何特性來探究突破.

解 ①當點B′落在AD邊上時，如圖6所示，根據矩形性質和折疊特性可知∠BAE=∠B′AE=■∠BAD=45°，則AB=BE，所以■a=1，從而解得a=■.

②當點B′落在CD邊上時，如圖7所示，根據矩形性質可得∠BAD=∠B=∠C=∠D=90°，AD=BC=a. 根據折疊過程可得∠B=∠AB′E=90°，AB=AB′=1，EB=EB′=■a，可推知DB′=■，EC=BC-BE=■a. 進一步分析可證△ADB′∽△B′CE，由相似性質可得■=■，從而可解得a1=■，a2=0（舍去）.

綜上可知，a的值為■或■.

折疊問題教學思考

上述對折疊問題突破的四種方法策略進行了實例探究，其解析思路和方法技巧具有一定的參考價值，而在實際教學折疊問題時需考慮學情和考情，針對問題特點和學生的學習能力進行教學，下面提出幾點教學建議.

1. 立足數學關系，奠定解題基礎

幾何的定理定義是解決折疊問題的基本工具，上述所探討的四大解題策略涉及幾何的軸對稱關系、全等關系、垂直平分、幾何特性等內容，在教學中需要對這些關系進行梳理. 例如引導學生理解幾何折疊過程中隱含的軸對稱現象，折疊前后的圖形關于折痕對稱. 對于其中的折疊特性則需要從線段長、幾何角大小和圖形形狀等方面進行總結闡釋. 教師要引導學生關注其中的特殊關系，如直角三角形的三邊關系，相似三角形對應邊的比的關系等，讓學生掌握圖形折疊的內在規律，充分聯合其中的數學關系來構建思路.

2. 滲透數學思想，提升折疊價值

圖形折疊問題突破過程中滲透著眾多的數學思想，開展折疊問題的數學思想教學可以提升考題的價值.折疊問題建立在空間平面上，其中涉及線段長的數量關系，同時隱含著數學的函數思想、方程思想等.對于以折疊為背景的幾何問題，在實際教學中不應局限于基本的幾何定理，而應以折疊為基礎滲透數學思想方法.例如上述例4的探究中以勾股定理和相似性質為基礎，融合方程思想來構建關于參數的解析方程.數學解題應重視其中的思想方法，靈活運用數學思想來指導思路構建，可快速打開解題突破口，這對學生的思維發展是十分有利的.

3. 關注折疊構造，發展核心素養

圖形折疊是初中數學的重難點內容，其動態過程中隱含著眾多“變”與“不變”的關系，教學中若僅通過圖形探究很難使學生充分掌握問題的突破方法，也不容易形成折疊問題的突破策略.本文建議教學中應結合具體的折疊實例，從添加輔助線入手來幫助學生掌握折疊問題的構造方法.例如連接對應點，利用連線與折痕的垂直關系來構建直角三角形;完善折疊圖形，利用折疊前后的全等關系來提取等量關系.構造圖形是初中階段需要學生重點掌握的方法技巧，對于幾何問題的突破至關重要，教師在教學中應重視圖形構造，以幾何構造為基礎來發展學生的構造思想，逐步提升學生的核心素養.

結束語

折疊問題的突破策略眾多，上述所呈現的只是其中較為常用的幾種，而在實際解析時需要根據問題特點、圖形結構靈活變通.另外圖形折疊中隱含的定理是圖形折疊的本質體現，教師在教學中需引導學生深入挖掘，重點體會，融合數學的思想方法來提升學生的數學思維.