具有分級(jí)免疫率的SIRA計(jì)算機(jī)病毒模型

李杏 趙向青 鄒秉辰

【摘要】在殺毒軟件等防御措施下，健康機(jī)和感染機(jī)都在一定程度上獲得了免疫力，但往往后者比前者強(qiáng)。基于這種認(rèn)識(shí)，在SIRA模型基礎(chǔ)上研究分層免疫效應(yīng)，探索分層免疫效應(yīng)對(duì)系統(tǒng)穩(wěn)定性的影響。研究了分層免疫機(jī)制下SIRA模型無(wú)毒平衡點(diǎn)和有毒平衡點(diǎn)的穩(wěn)定性，并對(duì)理論結(jié)果做了數(shù)值仿真。

【關(guān)鍵詞】分級(jí)免疫率;SIRA;穩(wěn)定性;數(shù)值仿真

【中圖分類號(hào)】TP309.5

【文獻(xiàn)標(biāo)識(shí)碼】B

互聯(lián)網(wǎng)在為傳播資訊提供便利的同時(shí)也給計(jì)算機(jī)病毒的傳播提供了溫床。計(jì)算機(jī)病毒自我復(fù)制能力強(qiáng)，破壞力大，是互聯(lián)網(wǎng)的頭號(hào)敵人。在互聯(lián)網(wǎng)高速發(fā)展的今天，計(jì)算機(jī)病毒對(duì)網(wǎng)絡(luò)信息安全的威脅不得不引起高度重視。

計(jì)算機(jī)病毒與傳染病病毒在傳播機(jī)理上有很大的相似性，從20世紀(jì)80年代末期開始人們便借鑒傳染病模型研究計(jì)算機(jī)病毒，詳見表1。

其中S，I，R，A分別代表易感染計(jì)算機(jī)，已感染計(jì)算機(jī)，臨時(shí)免疫計(jì)算機(jī)，永久免疫計(jì)算機(jī);β代表病毒發(fā)生率;a，a2分別表示S計(jì)算機(jī)和I計(jì)算機(jī)直接轉(zhuǎn)為A計(jì)算機(jī)的概率（即免疫率）;δ代表臨時(shí)免疫率;σ代表重復(fù)感染率;N代表外部計(jì)算機(jī)連入網(wǎng)絡(luò)的速率;μ代表淘汰率。

在計(jì)算機(jī)安裝殺毒軟件后，計(jì)算機(jī)在一定程度上對(duì)病毒產(chǎn)生了“免疫力”。但健康機(jī)和感染機(jī)的免疫力是不一樣的，通常后者免疫力高于前者。基于這種認(rèn)識(shí)，楊茂斌在SLBRS模型基礎(chǔ)上考慮了分級(jí)免疫機(jī)制。本文研究分級(jí)免疫率SIRA模型，探索平衡點(diǎn)的穩(wěn)定性。

2 分級(jí)免疫SIRA模型

現(xiàn)實(shí)中R計(jì)算機(jī)也可以轉(zhuǎn)化為A計(jì)算機(jī)，設(shè)轉(zhuǎn)化概率a3，則模型（1）改進(jìn)為如下的：

4 穩(wěn)定性仿真

4.1 無(wú)毒平衡點(diǎn)的穩(wěn)定性

取定以下參數(shù)a1= 0.025，a2=0.25，a3=0.15，β=0.1，σ=0.8，δ= 0.6.N=0.2，μ=0.2，此時(shí)計(jì)算得k1=0.125

圖2顯示系統(tǒng)中四種狀態(tài)計(jì)算機(jī)隨時(shí)間的變化規(guī)律。其中S計(jì)算機(jī)從初始狀態(tài)逐漸增加到最大值并穩(wěn)定下來(lái)，I計(jì)算機(jī)、R計(jì)算機(jī)和A計(jì)算機(jī)從初始值逐漸減小并趨于零。因此系統(tǒng)最終穩(wěn)定在無(wú)毒平衡點(diǎn)（1，0，0，0），與定理l結(jié)論吻合。

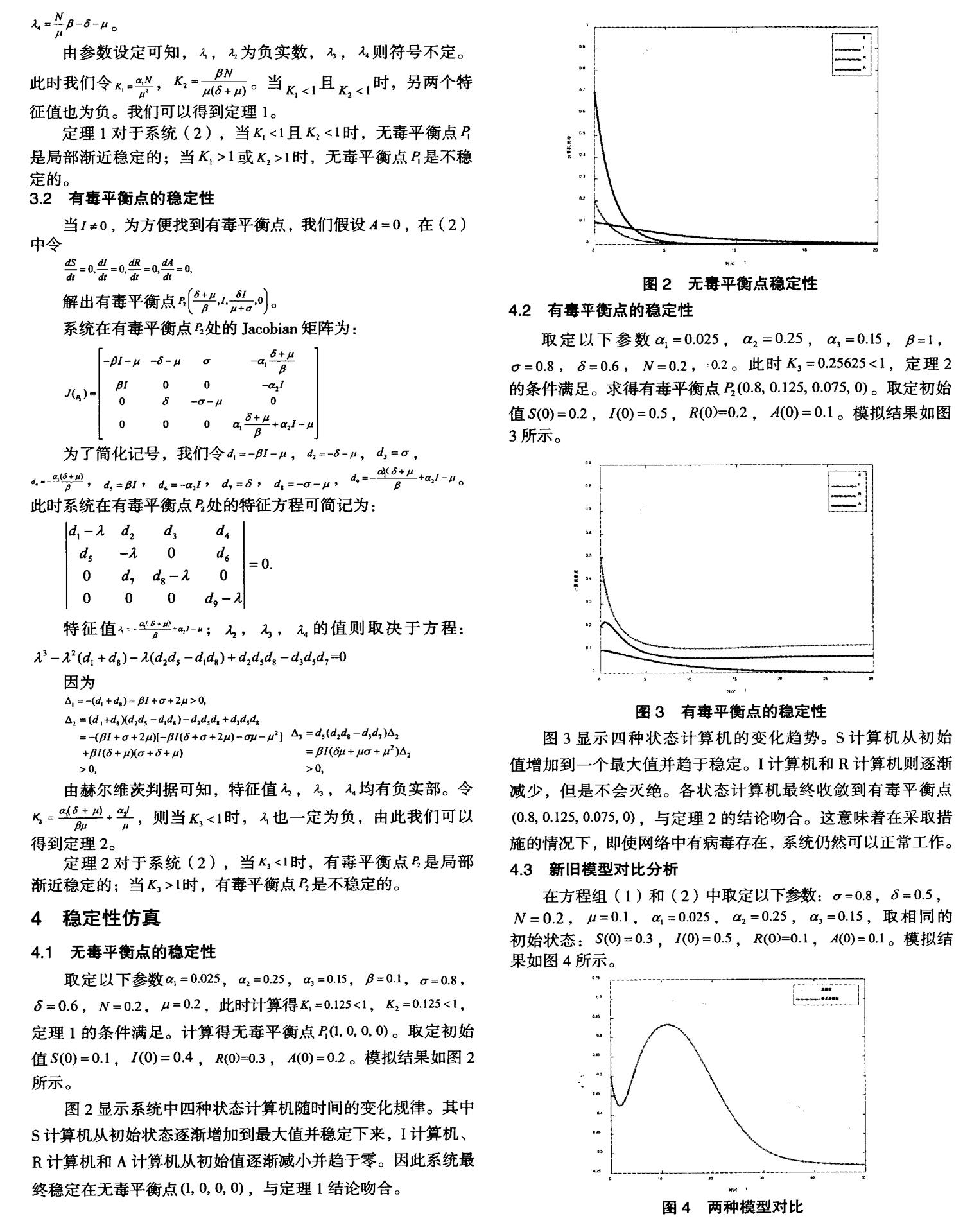
4.2 有毒平衡點(diǎn)的穩(wěn)定性

取定以下參數(shù)a1= 0.025，a2= 0.25，a3= 0.15，β=1，σ=0.8，δ=0.6，N=0.2，：0.2。此時(shí)K3= 0.25625<1，定理2的條件滿足。求得有毒平衡點(diǎn)P2 （0.8，0.125，0.075，0）。取定初始值S（0）=0.2，I（0）=0.5，R（0）=0.2，A（0）=0.1。模擬結(jié)果如圖3所示。

圖3顯示四種狀態(tài)計(jì)算機(jī)的變化趨勢(shì)。S計(jì)算機(jī)從初始值增加到一個(gè)最大值并趨于穩(wěn)定。I計(jì)算機(jī)和R計(jì)算機(jī)則逐漸減少，但是不會(huì)滅絕。各狀態(tài)計(jì)算機(jī)最終收斂到有毒平衡點(diǎn)（0.8，0.125，0.075，0），與定理2的結(jié)論吻合。這意味著在采取措施的情況下，即使網(wǎng)絡(luò)中有病毒存在，系統(tǒng)仍然可以正常工作。

4.3 新舊模型對(duì)比分析

在方程組（1）和（2）中取定以下參數(shù)：σ=0.8，δ=0.5，N=0.2，μ=0.1，a1=0.025，a2=0.25，a3=0.15，取相同的初始狀態(tài)：S（0）=0.3，I（0）=0.5，R（0）=0.1，A（0）=0.1。模擬結(jié)果如圖4所示。

圖4表明了在同一時(shí)間，其他條件相同的情況下，分層免疫SIRA模型對(duì)感染節(jié)點(diǎn)的反應(yīng)更加明顯，比原模型表現(xiàn)得更優(yōu)秀。

5 結(jié)論

在SIRA模型的基礎(chǔ)上，考慮到除了S和I，R也可以通過(guò)采取防護(hù)措施轉(zhuǎn)化為A狀態(tài)的計(jì)算機(jī)，且計(jì)算機(jī)的免疫率是有高低之分的，即a2>a3。本文將不同的免疫率結(jié)合起來(lái)考慮，正如我們所預(yù)期的那樣，系統(tǒng)在分層免疫的情況下會(huì)更加穩(wěn)定。

[參考文獻(xiàn)]

[1] J.O.Kephart，S.R.White. Directed-graph epidemiological models ofcomputer vim8es[J].IEEE Symposium on Security and Privacy，1991，343—361.

[2] J.C.Wierman，D.J.Marchette.Modeling computer vinls prevalencewith a susceptible—i也cted—susceptible model“th reintroduction[J].Computational Statistics and Data AnaIysis，2004，45（1）：3—23.

[3] J.R.C.Piqueira，V.0.Araujo.A modified epidemiological model forcomputer Viruses叨.Applied Mat}lematics and Computation，2009，213：355—360.

[4]楊茂斌，三種新型計(jì)算機(jī)病毒傳播模型：理論研究與應(yīng)用策略[D].重慶：重慶大學(xué)，2012.

[作者簡(jiǎn)介]李杏（1994-），女，碩士研究生，研究方向：農(nóng)業(yè)信息化;趙向青（1974-），男，湖南炎陵人，教授，研究方向：微分動(dòng)力系統(tǒng);鄒秉辰（1997-），女，江蘇徐州人，碩士研究生，研究方向：農(nóng)業(yè)信息化。