基于模型稀疏表示的單快拍波達方向魯棒估計

虞 飛，宋 俊，余 赟，龐巖澤

(海軍研究院，北京100071)

0 引 言

信號波達方向(Direction of Arrival,DOA)估計作為陣列信號處理中一項極為關(guān)鍵的研究內(nèi)容，已在無線電通信、雷達、聲吶、導(dǎo)航、地震探測等領(lǐng)域有著廣泛的應(yīng)用[1]。在實際環(huán)境中，由于多徑傳播等因素的影響，相干信號是普遍存在的。對于傳統(tǒng)的以多重信號分類(Multiple Signal Classification,MUSIC)[2]和旋轉(zhuǎn)不變信號參數(shù)估計(Estimation of Signal Parameters via Rotational Invariance Techniques,ESPRIT)[3]算法為代表的子空間類DOA估計算法，由于相干信號源的信號子空間秩個數(shù)小于信號源數(shù)，導(dǎo)致DOA估計的準(zhǔn)確度嚴(yán)重下降甚至估計失敗。另外，目標(biāo)平臺(如艦艇、飛機等)在實際工作時經(jīng)常是快速機動的，特殊情況下需要做復(fù)雜而高速的機動動作。這就要求在采樣時間內(nèi)，目標(biāo)信號需持續(xù)入射到陣列，而且入射的信號個數(shù)、信號的波達方向不能發(fā)生變化。在信號源高速運動、信道快速時變等場合，我們無法進行足夠長時間的采樣，這時只有少數(shù)的快拍可以利用，極端情況下只有一次快拍，此時，基于多快拍數(shù)據(jù)的DOA估計算法已經(jīng)無法適用[4-5]。

近年來，基于稀疏表示框架的陣列參數(shù)估計方法引起了相關(guān)學(xué)者的廣泛關(guān)注，并取得了大量高質(zhì)量的研究成果[6-11]。這類方法的顯著優(yōu)點是它們在有限采樣快拍數(shù)據(jù)、相干多徑信號、陣列模型誤差、信號DOA角度間隔小等非理想條件下，都具有很好的魯棒性。考慮到在實際應(yīng)用中，目標(biāo)信號個數(shù)遠小于傳感器陣元數(shù)，目標(biāo)信號DOA相對于空間來說也是稀疏的，本文將傳統(tǒng)的傳感器陣列輸出模型進行稀疏化表示，得到陣列輸出數(shù)據(jù)的稀疏表示模型，研究了一種基于l1-范數(shù)最小化的單快拍DOA估計算法(簡稱L1-min算法)。該算法將稀疏參數(shù)求解問題轉(zhuǎn)化為二階錐規(guī)劃(Second-Order Cone Programming，SOCP)問題的一般形式，并在二階錐規(guī)劃的框架下求解[12]，同時探討了算法中正則化參數(shù)的選取依據(jù)。L1-min算法在小樣本、相干多徑信號、目標(biāo)信號角度間隔小等非理想條件下具有很好的估計性能。

1 陣列輸出模型

考慮K個遠場窄帶信號入射到由M個無方向性(全向)陣元構(gòu)成的均勻線性陣列(Uniform Linear Array,ULA)，并假設(shè)K個信號與ULA在同一平面內(nèi)(在實際應(yīng)用場景中，如水下聲吶基陣測向，我們經(jīng)常只關(guān)心某一平面內(nèi)信號的入射方位，或者入射信號在該平面內(nèi)的投影，因此，這一假設(shè)可以得到保證)[13]。將陣元由1到M進行編號，并以陣元1作為基準(zhǔn)或參考陣元。設(shè)參考陣元處的任一接收信號變換到基帶后有如下形式[14]：

那么，在t時刻，整個陣列的M×1維輸出數(shù)據(jù)模型為

式中，s(t)=[s1(t)…s(t)]T為變換到基帶后的參考K陣元處接收到的K個信號構(gòu)成的列向量，n(t)=[n1(t),…,nM(t)]T為陣列的零均值加性復(fù)高斯白噪聲向量，A=[a(θ1)…a(θK)]為M×K維導(dǎo)向矢量矩陣，且對于ULA，導(dǎo)向矢量a(θk)可定義為[15]

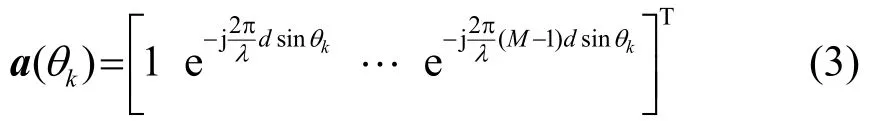
式中，d為相鄰陣元間距，λ為信號波長，θk為第k個信號的波達方向(DOA)，通常定義為該信號入射方向與ULA法線方向的夾角，則有θk∈[- π/2,π/2]。

2 模型的稀疏表示與稀疏矩陣方程的求解

直接求解優(yōu)化問題式(5)，必須篩選出向量γ(t)中所有可能的非零元素，由于搜索空間過于龐大，故此方法是非確定性多項式時間(Non-deterministic Polynomial-time,NP)困難的。

考慮到l1-范數(shù)是最接近于l0-范數(shù)的凸目標(biāo)函數(shù)，目前，使用最廣泛的求解方法是將l0-范數(shù)最小化問題(5)轉(zhuǎn)化為凸松弛的l1-范數(shù)最小化問題(簡稱L1-min算法)，即：

首先，將l1-范數(shù)最小化問題(6)轉(zhuǎn)化為標(biāo)準(zhǔn)SOCP問題形式。

式中，ei為N×N維單位陣I的第i行構(gòu)成的一個1×N維行向量，Re[·]和Im[·]分別表示取實部和取虛部。

證明：因為

也即

又因為

所以，結(jié)論(1)得證。

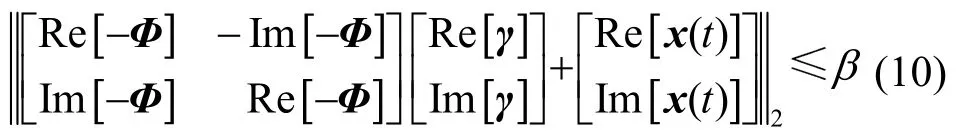
由(1)、(2)，則式(6)中的原l1-范數(shù)最小化問題轉(zhuǎn)化為如下形式的標(biāo)準(zhǔn)SOCP問題：

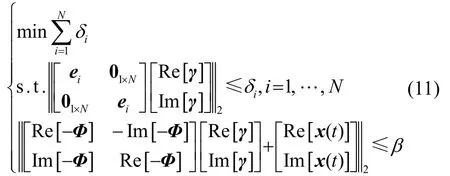
3 仿真實驗

3.1 兩個獨立信號情形

考慮兩個獨立信號分別以DOA參數(shù)θ1=-10°，θ2=60°入射到上述均勻線陣，圖1給出了基于L1-min算法和常規(guī)波束形成算法(Conventional Beamforming,CBF)得到的歸一化空間功率譜圖。圖2給出了兩個獨立信號分別以DOA參數(shù)θ1=-10°，θ2=-5°入射到上述均勻線陣時，基于以上兩種算法得出的歸一化空間功率譜圖。

圖1 角度間隔較大的兩個獨立信號DOA估計的歸一化空間功率譜Fig.1 Normalized spatial power spectrum for DOA estimation of two independent signals with large angular spacing

由圖1的仿真曲線可以看出，當(dāng)目標(biāo)信號的角度間隔較大時，采用L1-min算法和CBF算法均可以在真實的目標(biāo)方向上形成譜峰。而且，本文算法的譜峰比CBF算法更加尖銳，更加對準(zhǔn)目標(biāo)真實方向，旁瓣比CBF算法的旁瓣也低得多。由圖2的仿真結(jié)果可發(fā)現(xiàn)，當(dāng)目標(biāo)信號的角度間隔較小時，本文提出的 L1-min算法仍能在真實的目標(biāo)方向上形成尖銳的譜峰。相反，CBF算法在兩個真實的目標(biāo)方向上的譜峰合二為一，說明此時CBF算法無法分辨兩個信號的DOA。綜合圖1和圖2可知，對于獨立信號的情形，L1-min算法對目標(biāo)信號DOA估計的精度和分辨率都比CBF算法高。

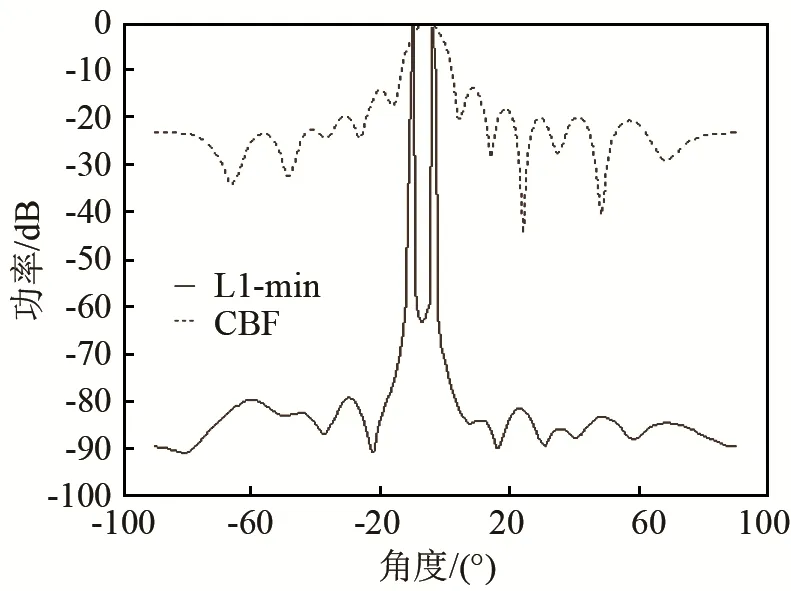
圖2 角度間隔較小的兩個獨立信號DOA估計的歸一化空間功率譜Fig.2 Normalized spatial power spectrum for DOA estimation of two adjacent independent signals

3.2 兩個相干信號情形

圖3 角度間隔較大的兩個相干信號DOA估計的歸一化空間功率譜Fig.3 Normalized spatial power spectrum for DOA estimation of two coherent signals with large angular spacing

由圖3的仿真曲線可以看出，當(dāng)相干信號的角度間隔較大時，采用L1-min算法和CBF算法均可以在真實的目標(biāo)方向上形成譜峰，與圖 1相比發(fā)現(xiàn)，兩個算法的估計精度和分辨率并沒有因為信號相干而有顯著下降。但本文算法的譜峰比CBF算法更加尖銳，更加對準(zhǔn)目標(biāo)真實方向，旁瓣比CBF算法的旁瓣也低得多，而且CBF算法旁瓣的高度與主瓣高度相差變小。由圖4的仿真結(jié)果可發(fā)現(xiàn)，當(dāng)相干信號的角度間隔較小時，本文提出的L1-min算法仍在真實的目標(biāo)方向上形成了尖銳的譜峰。相反，CBF算法在兩個真實的目標(biāo)方向上的譜峰合二為一，說明此時 CBF算法無法辨別兩個信號的DOA。綜合圖3和圖4可知，對于相干信號的情形，L1-min算法對目標(biāo)信號DOA估計的精度和分辨率都比CBF算法高。

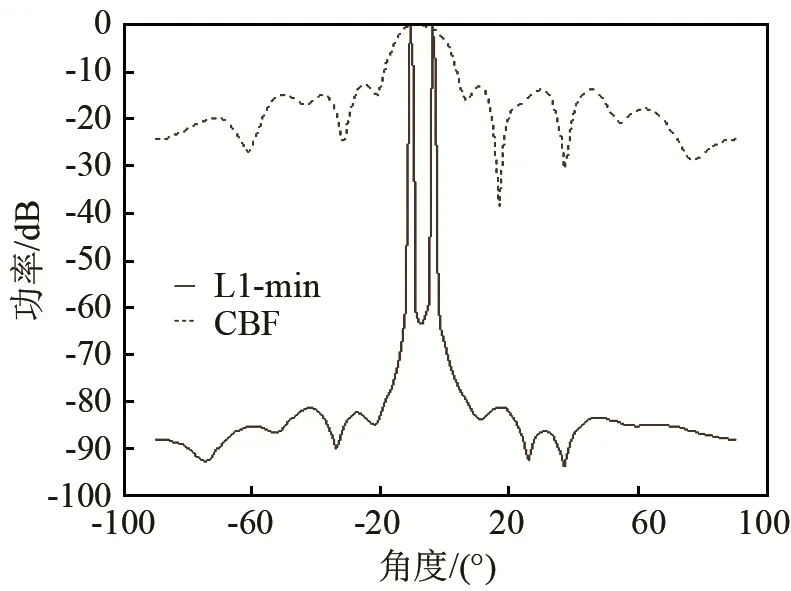
圖4 角度間隔較小的兩個相干信號DOA估計的歸一化空間功率譜Fig.4 Normalized spatial power spectrum for DOA estimation of two adjacent coherent signals

需要說明的是，本仿真實驗中的信噪比 SNR為15 dB。在低信噪比情況下，無論目標(biāo)信號之間是否相關(guān)，本文算法仍能在真實的目標(biāo)角度附近形成明顯的尖峰。只是隨著信噪比的降低，算法對目標(biāo)信號DOA的估計精度會有所下降，歸一化稀疏功率譜的旁瓣級有所升高，但并不影響本文算法對DOA的整體估計效果。

4 結(jié) 論

本文對傳統(tǒng)的傳感器陣列輸出模型進行了稀疏重構(gòu)，提出了一種凸松弛的l1-范數(shù)最小化 DOA估計算法(L1-min)，給出了l1-范數(shù)最小化優(yōu)化問題的詳細求解方法，分析了算法中正則化參數(shù)的選取依據(jù)。仿真結(jié)果表明，本文算法在單快拍、相干多徑信號、目標(biāo)信號空間間隔很小等非理想情況下都具有較好的估計精度和分辨率，因而非常適用于快變相干信號DOA的實時跟蹤估計。本文同時指出，正則化參數(shù)的選取直接關(guān)系到最終的稀疏恢復(fù)性能，然而在很多情況下，對正則化參數(shù)的選擇是很困難的，尤其是在對噪聲的統(tǒng)計特性一無所知的情況下，這也是L1-min算法的局限性所在。事實上，正則化參數(shù)對噪聲的統(tǒng)計特性和信噪比十分敏感。因此，研究提出一類無需進行正則化參數(shù)選取的稀疏參數(shù)估計算法是后續(xù)值得研究的問題。