自適應圖學習誘導的子空間聚類

朱 丹，陳曉紅，吳卿源，李舜酩

1.南京航空航天大學 理學院，南京 211106

2.南京航空航天大學 能源與動力學院，南京 211106

1 引言

在機器學習領域，子空間聚類受到廣泛關注，可用于人臉聚類[1-2]、運動分割[3-4]等。子空間聚類方法是將特征選擇技術和聚類技術相結合，在維度空間或數據空間中搜索可能存在的子空間，從而得到相應的子空間和聚類產生的簇[5]。具體而言，給定一組來自k個線性子空間{S1,S2,…,Sk} 的數據集X，X=[X1,X2,…,Xk]=[x1,x2,…,xn] ，其中Xi是子空間Si中樣本構成的集合，子空間聚類的目標是將數據集X分成k個不同的簇，每一簇對應一個子空間。

迄今為止，人們提出了多種子空間聚類的方法，按照其原理大致可分為五種：矩陣分解法[6]、代數方法[7]、迭代方法[8]、統計方法[9-10]和基于譜聚類的方法[2-3]。本文基于譜聚類的方法進行研究。首先，利用給定的數據集X，構造關聯矩陣Z，Z中的每個元素zij衡量了樣本點xi和xj之間的相似性。數據集中的每一個樣本點能用其他的樣本點的線性組合表示出來，因此可以使用樣本自表示來衡量兩個樣本點的相似性[11]，然后根據關聯矩陣Z進行譜聚類。譜聚類是基于譜圖理論的聚類算法，關聯矩陣Z可以被看作圖，數據聚類問題轉變為圖最優切割問題。由于塊對角圖能夠更準確地描述數據聚類結果，因此通常期望關聯矩陣Z具有塊對角稀疏性。

以下幾種算法都是基于譜聚類的方法，但是其關聯矩陣有所不同。稀疏子空間聚類（Sparse Subspace Clustering，SSC）[3]通過對關聯矩陣Z采用稀疏約束得到了稀疏的塊對角陣。文獻[12]指出如果一組樣本點間的兩兩相關性很高，稀疏表示往往隨機選擇其中一對樣本點。因此，SSC不能夠很好地捕獲同一子空間的數據結構關系，可能會將同一類簇的點分到不同類簇，得到錯誤的聚類結果。由此可見，SSC雖然獲得了簇間的稀疏性，但是同時也會導致簇內稀疏，從而使得聚類結果并不理想。為了彌補SSC 的不足，Liu 等人[13]提出用低秩表示（Low Rank Representation，LRR）來代替稀疏表示。低秩表示在構造關聯矩陣時加入了低秩約束，目的是考慮數據的全局結構，找到數據的低秩表示，根據這種表示可把來自同一子空間的樣本點聚到一起。低秩約束可以有效降低噪聲數據的影響，因此LRR對噪聲和異常值具有較好的魯棒性。文獻[1]中的Example-1表明了當子空間正交時，LRR模型并不能保證得到一個塊對角陣，因此低秩表示不能保證得到正確的聚類結果。為了得到塊對角陣，Lu等人[1]提出了最小二乘回歸（Least Square Regression，LSR），通過分組效應，即一組相關數據的系數近似相等，將高度相關的數據聚集到了一起。當子空間正交或者子空間獨立、樣本數據充足時，LSR 能夠得到塊對角矩陣，但是由于LSR 沒有考慮數據間的局部相關性，導致塊對角陣過于稠密。

以上方法均是在單視圖數據上展開的，而文獻[14]認為多視圖學習比單視圖學習方法有更好的泛化性，將單視圖數據多視圖化可提高學習效果。首先將單視圖數據多視圖化[15]，得到多視圖數據。這些多視圖數據的不同視圖間的信息具有一致性和互補性[16]。而協同訓練算法正是利用了不同視圖數據的信息互補，提高了算法性能，受此啟發，本文提出了一種自適應圖學習誘導的子空間聚類算法（Subspace Clustering induced by Adaptive Graph Learning，SCAGL）。首先，通過多視圖化的方法對原本的數據集進行特征分割，得到多視圖數據集。然后，受到多視圖譜聚類協同訓練的啟發[17]，將多視圖數據子空間聚類與協同訓練的思想相結合。通過建立引入圖正則化項的最小二乘回歸模型，對多個視圖進行子空間聚類，基于協同訓練的思想，使視圖間的圖信息可以互相利用，對多個視圖的圖正則化項進行優化，能夠得到聚類性能更好的塊對角關聯矩陣。最后，對每個視圖學習到的關聯矩陣進行集成得到一個公共的關聯矩陣，并以此進行譜聚類。本文的貢獻在于：受協同訓練的啟發，有效地利用不同視圖間的聚類信息，自適應地迭代更新每個視圖的相似矩陣，從而得到更能反映聚類效果的塊對角圖，即塊對角關聯矩陣，它能更準確地描述數據聚類結果。雖然該方法是針對單視圖數據提出的，它也可應用于多視圖數據。

2 相關工作

2.1 最小二乘回歸

假設樣本數據充足且子空間獨立，Lu 等人提出了基于最小二乘回歸（LSR）的子空間聚類[1]。數據集X=[x1,x2,…,xn] ∈Rd×n，d是特征維數，n是樣本個數，數據集中的每一個樣本點能用其他的樣本點的線性組合表示出來即X=XZ，為避免平凡解，規定diag(Z)=0 。Z∈Rn×n為自表示系數矩陣。LSR 的目標方程如下：

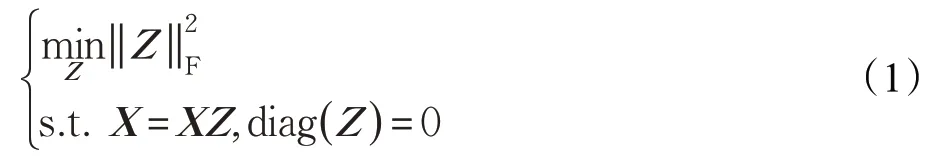
‖Z‖F是Z的F 范數，該范數約束使得自表示系數矩陣Z塊對角化，去除Z中較小的系數[18]。

由于真實數據中通常包含噪聲，為了減少噪聲對聚類效果的影響，LSR 引入誤差項E∈Rd×n，即X=XZ+E。LSR對誤差項實行F范數約束，該方法可處理高斯噪聲。文獻[18]已證對誤差項E實行L2,1范數可以探測異常值，得到如下的目標函數：

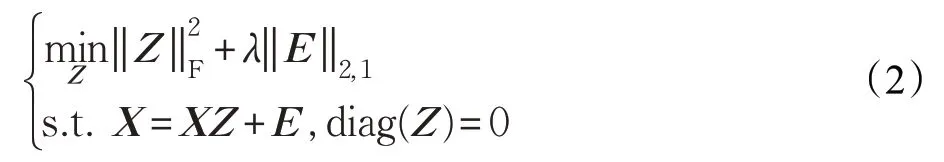
其中，λ為誤差項的參數。當子空間正交或數據集充足，子空間獨立時，F 范數約束使得Z具有好的塊對角性，自表示系數矩陣Z能夠表示樣本間的相似性。但是，優化如上目標函數得到的Z是稠密的，為了提高Z的稀疏性，通常引入圖正則化項。

2.2 引入圖正則化項

LSR 在一定程度上提高了Z的塊對角性質，但其只揭示了樣本的全局信息，并沒有考慮到數據點的局部內在相關信息，從而導致自表示系數矩陣Z過于稠密。已有的研究表明[19-21]引入圖正則化項有利于保留數據的局部內在信息，對Z的非對角塊部分進行稀疏約束，使得聚類效果更好。

首先由數據集X構造圖G=(V,E)，V:={1,2,…,n}是頂點集，是邊緣權重的集合，wij是頂點對(i,j)的邊緣權重，權重矩陣W=(wij)n×n，本文主要使用k近鄰來構造兩個樣本點間的權重。由于G是無向圖，W=WT。度量矩陣D=diag(d1,d2,…,dn)，，圖G的拉普拉斯矩陣L=D-W，從而得到目標函數：

其中，β是圖正則化項參數。圖正則化項tr(ZLZT)目的是希望同一類簇的樣本之間的系數盡可能的一致。由于，目標方程也可寫為：

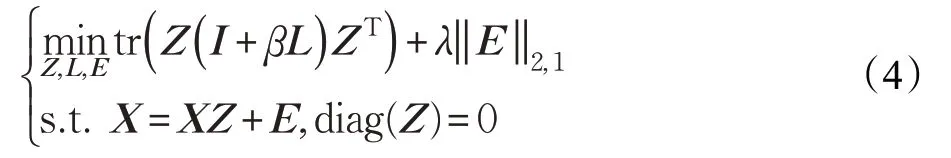
2.3 多視圖化的子空間聚類

文獻[15]提出了將單視圖數據多視圖化的方法，即，對數據集X∈Rd×n進行分割率為α(0＜α ＜1) 的分割，得到s個新的子特征數據集，這s個子特征數據集可看做樣本數據集的s個不同的視圖。對這s個視圖的數據，基于圖正則化的最小二乘回歸進行聚類，可得到s個對應的塊對角系數矩陣，這可表示為：

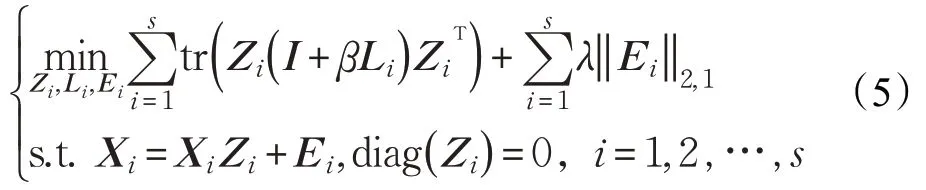
如此得到各個視圖對應的自表示系數矩陣Zi，由于每個視圖的數據信息具有一致性和互補性，由式（5）得到的Zi包含著許多公共信息。文獻[22]提出了最優自表示系數矩陣Z*，與Z*相比，每個視圖的自表示系數矩陣Zi包含著各種噪聲，Z*滿足下式：

不難解得：

3 自適應圖學習

3.1 協同訓練算法

協同訓練算法是由Blum A和Mitchell T提出的一種半監督學習算法[23]，協同訓練算法適用于其特征可以自然分割為幾個不相交特征集的數據集，在每個特征集上學習分類器，并通過結合這些分類器的預測結果，提高分類的正確率。文獻[24]發現當特征集非常大且包含大量冗余特征時，把特征集劃分為多視圖數據集，協同訓練算法可取得很好的效果。該文通過單視圖數據多視圖化，得到s個不同的視圖X1,X2,…,Xs，利用標記樣本訓練出s個分類器h1,h2,…,hs，分類器hi從未標記樣本中挑選若干個標記置信度高的樣本進行標記，把這些由hi標記過的樣本加入另外s-1 個分類器的訓練集中，以便其他分類器利用這些新增的有標記的樣本進行更新。這個過程不斷迭代下去，直到s個分類器不再發生變化。

協同訓練算法的成功實現需要滿足三個前提：（1）每個視圖能夠單獨地進行學習，即單視圖能夠學習出一個較好的分類器。（2）協同訓練算法要求目標函數在每個視圖上的學習結果相似度高。如果在某個視圖內，分類器判斷兩個樣本點屬于同一類簇，那么在其他視圖上也應該屬于同一類簇，若兩個樣本屬于不同類簇，其他視圖上也應該屬于不同類簇。（3）對于類別標記而言，不同視圖是條件獨立的。

3.2 基于協同訓練優化圖結構

受協同訓練的啟發，將其用于子空間聚類。每個視圖上構造出的權重矩陣Wi包含該視圖內樣本之間的信息，每一列向量win表示第n個樣本與其他樣本間的相似度。根據相似矩陣Wi構造Laplacian圖，由譜聚類算法[25]可知，圖Laplacian 矩陣Li的前c個特征向量組成特征矩陣Ui，Ui中的每個列向量代表一個簇，對Ui進行k-means聚類。如果矩陣Ui的第n行分配給第k類簇，樣本點xn就被聚到第k簇。因此Ui中的每個列向量是c個類簇的指示向量，包含了c個類簇的判別信息。受協同訓練思想的啟發，文獻[17]提出用其他視圖的聚類信息來迭代更新每個視圖的相似矩陣，再對該視圖的圖結構進行優化。包含了各視圖對聚類的判別性信息，將相似向量投影到這些特征向量的方向上，以保留聚類所需要的信息，并去除影響聚類結果的簇內信息。然后將其反投影到原始的向量空間中，獲得優化后的圖結構，即相似度矩陣進一步，在雙視圖情況下舉例驗證了優化后的相似矩陣顯示同一類簇內樣本間的相似度會逐步趨于一致，這有助于將不同類簇分開。文獻[22]中提出了使用本視圖的信息來迭代更新相似矩陣的方法，即得到了較好的聚類結果。這說明本視圖的信息有利于提高聚類的效果，結合以上兩種思想，本文提出同時把本視圖和其他視圖的信息融入聚類過程，迭代更新相似矩陣由于不同視圖的近鄰信息具有一致性，使用所有視圖的類簇信息來更新相似矩陣，這種新的方法使視圖間的信息相互傳遞，由此得到的相似矩陣包含更準確的聚類信息。

3.3 模型建立與算法流程

在式（5）基礎上引入圖結構優化，得到目標方程：

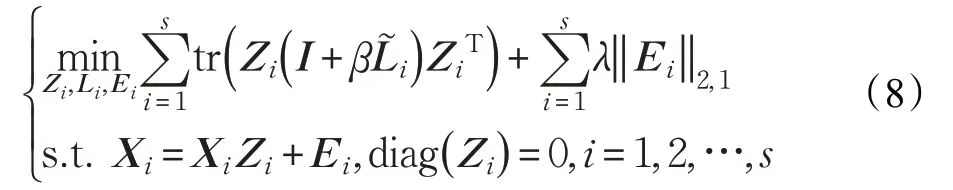
利用增廣拉格朗日乘子法[26-27]對目標方程（8）進行求解，其增廣拉格朗日方程為：

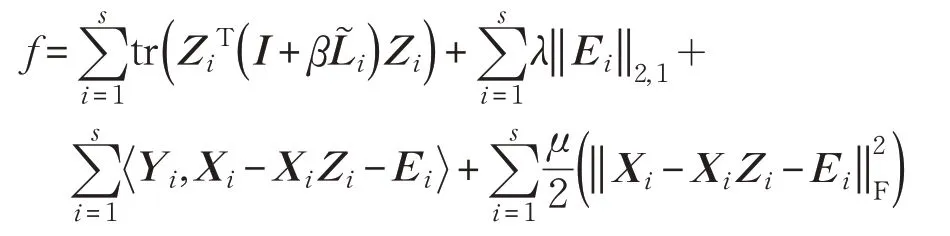
其中，μ ＞0 為懲罰系數，Yi為拉格朗日乘子，· 為矩陣的內積。分別對變量Zi,Li,Ei迭代優化求解。

（1）求解Zi

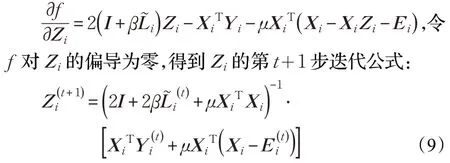
對數據集Xi構造權重矩陣Wi，并計算圖Laplacian矩陣Li，由Li的前c個最小的特征值對應的特征向量組成特征矩陣Ui，進而得到基于協同訓練算法優化后的相似度矩陣，對稱化后得。

（3）求解Ei：

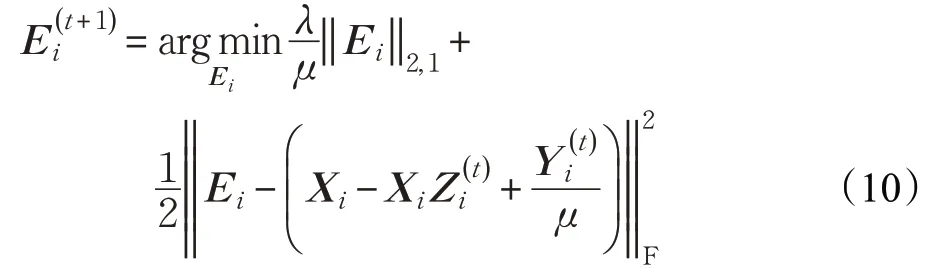
這可由收縮算子方法[28]求解。

本文提出自適應圖學習誘導的子空間聚類算法（SCAGL），輸入包含n個樣本的數據集X與目標類簇數c，通過該算法可將n個樣本聚到c個不同類簇，具體流程見如下算法。

算法1自適應圖學習誘導的子空間聚類（SCAGL）

輸入：數據集X，分割率α，誤差項參數λ，圖正則化參數β，聚類數c

輸出：c個類簇

1.對X的特征維進行分割率為α的多視圖化，得到s(s≥2 )個子特征數據集；

5.repeat

7.求得經過協同訓練優化后的圖Laplacian矩陣

9.更新各個視圖的乘子矩陣Yi=Yi+μ(Xi-XiZi-Ei)；

10.更新參數μ=min(ρμ,μmax)；

11.until max‖Xi-XiZi-Ei‖＜ε或達到最大迭代次數

13.計算關聯矩陣A=(Z*+Z*T)2；

14.對關聯矩陣A進行譜聚類，將數據分割到c個類簇中。

4 實驗結果與分析

4.1 數據集的選取

本文選取了4個不同數據集來進行實驗，人臉圖像數據集ORL、語音字母識別數據集Isolet、手寫數字數據集 USPS 和 mfeat。在這些數據集中，ORL、Isolet 和USPS是單視圖數據集，mfeat是多視圖數據集。

ORL 數據集包含了40 個不同人的人臉圖像，每個人在不同光照條件、拍攝場景和面部表情的情況下采集10張照片，將每張照片的大小修正為像素32×32。選取其中10 個人的照片生成一個100 個樣本的數據集進行實驗。

Isolet數據集是機器學習中用于聚類和分類的一種常用數據集。這個數據集的生成過程如下：150名試驗者將字母表中的每個字母讀兩遍，每個受試者有52 個訓練例子。數據集的特征維數是617，特征包括光譜系數、輪廓特征、聲波特征等。選取前30個人的訓練例子組成一個1 560個樣本的數據集進行實驗。

USPS 數據集是包含了數字0～9 的手寫數據集，數據集的特征維數是256，每個數字包含了1 100 個樣本。在 0～9 這 10 個數字中，手寫時 3、5、8 三個數字容易混淆。因此，在本實驗中選取3、5、8三個數字的樣本進行實驗。

mfeat 數據集是多視圖手寫數據集，是UCI 機器學習數據庫的一個重要組成部分，其中包含了6個不同的視圖 mfeat-fac、mfeat-fou、mfeat-kar、mfeat-mor、mfeatpix和mfeat-zer。每個視圖的特征維數不等，包含2 000個樣本，其樣本已經有標簽，即數字0～9，可用于對聚類算法分出的類簇進行評估。

4.2 聚類評價指標

4.2.1 歸一化互信息（Normalized Mutual Information，NMI）

互信息用來衡量兩個數據分布相關程度。設U和V是對n個樣本集合X的兩種不同聚類方法，記X={x1,x2,…,xn},U={U1,U2,…,UR},V={V1,V2,…,VC} ，首先定義互信息（MI）：

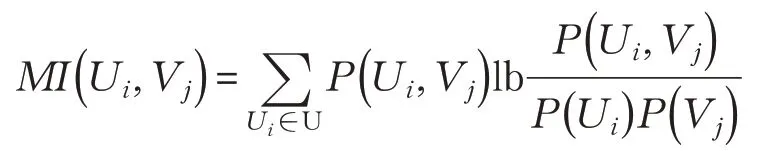
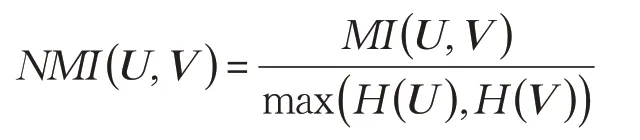
4.2.2 聚類準確率（Accuracy，ACC）

數據集X={x1,x2,…,xn} 包含了n個樣本，聚類準確率指的是正確聚類的樣本數占總樣本的比例。U是實驗得到的聚類結果，V為數據真實聚類結果，聚類準確率公式為：

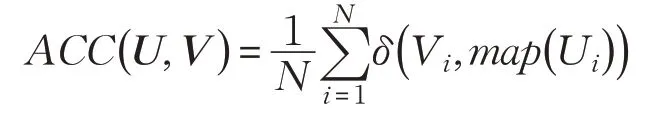
4.3 基準算法

本文選取了6種經典的聚類算法進行對比。（1）k均值聚類算法（k-means clustering algorithm）[29]直接在數據集X上進行實驗。（2）最小二乘回歸（Least Square Regression，LSR）[1]目標是，解析解為低秩表示子空間聚類（Low Rank Representation，LRR）[2]的目標是表示系數矩陣Z的核范數。（4）稀疏子空間聚類（Sparse Subspace Clustering，SSC）[3]的目標是表示系數矩陣Z的1-范數。（5）塊約束稀疏圖下的子空間聚類（Block-wise Constrained Sparse Graph，SGB）[18]。（6）塊約束下的集成子空間分割（Ensemble Subspace Segmentation Under Block-wise Constraints，ESSB）[22]。

與SSC、LRR、LSR、SGB 等算法相比，SCAGL 算法通過單視圖數據多視圖化將模型推廣到多視圖情形中，該算法不僅適用于單視圖數據，也可應用于多視圖數據。另外，與SGB、ESSB算法一樣，SCAGL算法引入了圖正則化項，利用了視圖內的近鄰信息。與ESSB算法相比，本文提出的算法使用所有視圖的聚類信息來更新相似矩陣，使不同視圖間的信息能夠相互傳遞，由此得到的相似矩陣包含更準確的聚類信息。幾種算法的對比參見表1。

表1 與基準算法的對比

4.4 實驗結果與分析

4.4.1 單視圖數據集上的實驗

首先選取3 個單視圖數據集ORL、Isolet 和USPS，為了計算聚類準確率和互信息，數據集的類簇標簽是已知的。

選取6種經典聚類算法進行對比，自適應圖學習誘導的子空間聚類（SCAGL）是本文提出的算法，其目標方程為式（8），該算法首先對數據進行多視圖化，將單視圖數據分割為多視圖數據，由于分割方式不同，多視圖化可分為順序多視圖化與隨機多視圖化。因此自適應圖學習誘導的子空間聚類（SCAGL）可以根據分割方式分為 SCAGL-original 和 SCAGL-random 兩種，SCAGL-original表示順序多視圖化后的聚類，SCAGL-random表示隨機多視圖化后的聚類。

對于這幾種不同的算法，在每個數據集上單獨執行30次實驗，取其均值作為評價指標，如表2和表3所示。

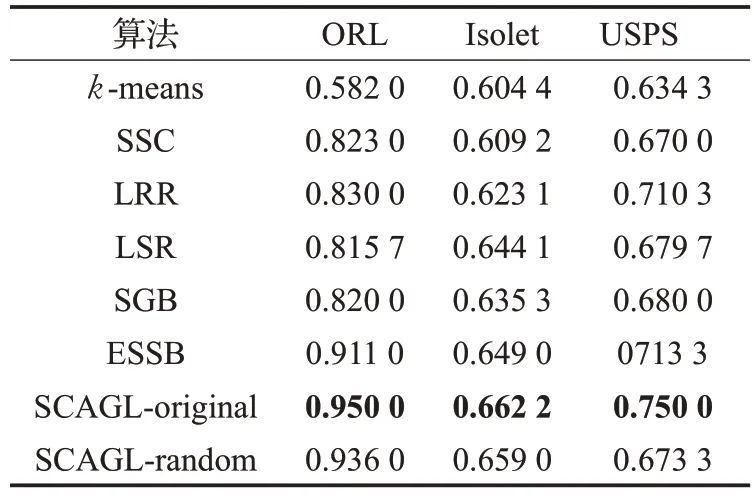
表2 在單視圖數據集上的聚類準確率（ACC）

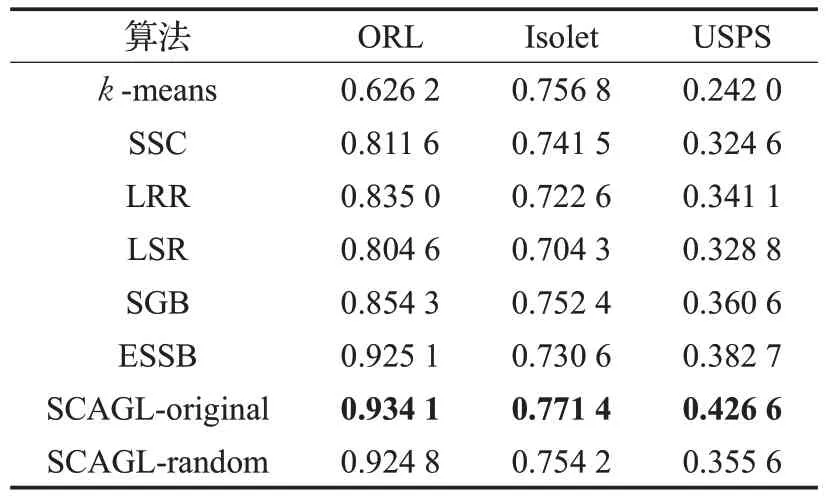
表3 在單視圖數據集上的歸一化互信息（NMI）

由表2和表3可見，引入圖正則化項后，算法的聚類性能普遍優于沒有圖正則化的算法。而與ESSB實驗結果相比較，利用所有視圖的聚類信息來迭代更新每個視圖的相似矩陣比僅僅使用本視圖的信息來更新相似矩陣得到的聚類結果要好。由此可見，不同視圖間的圖信息的共同利用至關重要。

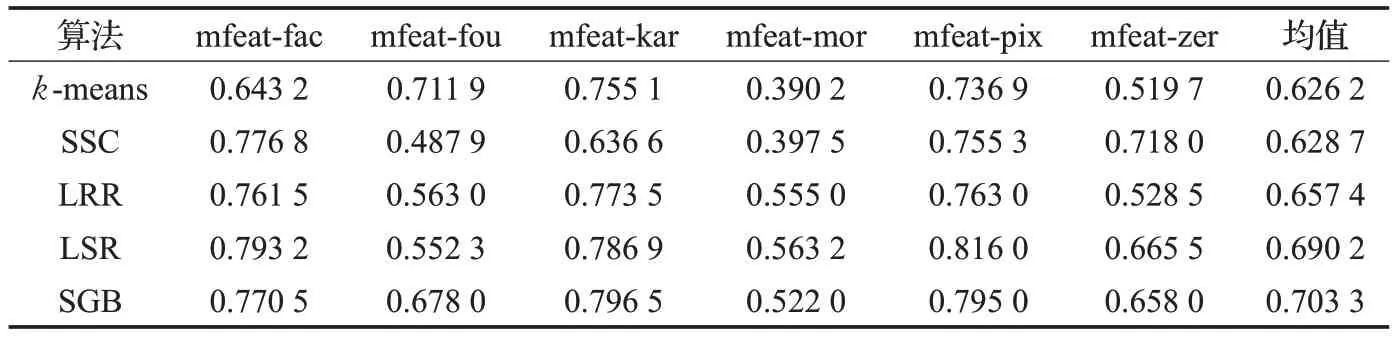
表4 在mfeat數據集上的聚類準確率（ACC）

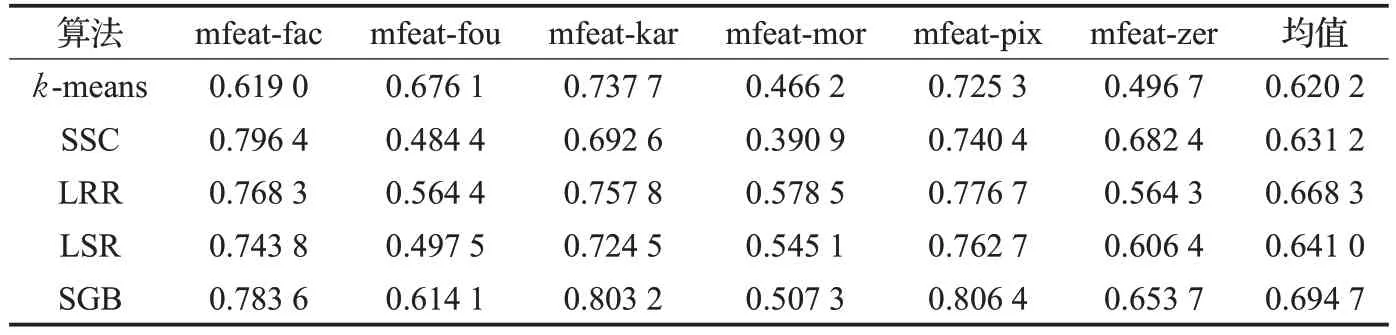
表5 在mfeat數據集上的歸一化互信息（NMI）

4.4.2 多視圖數據集上的實驗

在多視圖數據集mfeat 上進行實驗分析，該數據集包含了6個特征維數不等的視圖。k-means、SSC、LRR、LSR和SGB這5個算法均是在單視圖數據集上展開的，因此可以在該數據集的每個視圖上單獨進行實驗，然后計算出每個算法在6個視圖上得到的實驗結果的均值，如表4和表5所示。

SCAGL、ESSB算法在單視圖數據集上首先需要對數據進行多視圖化，將單視圖數據集分割為多視圖數據集，而mfeat本來就是多視圖數據集，因此可以直接在這兩個算法上進行實驗，得到的聚類準確率ACC 與歸一化互信息NMI的結果如表6所示。

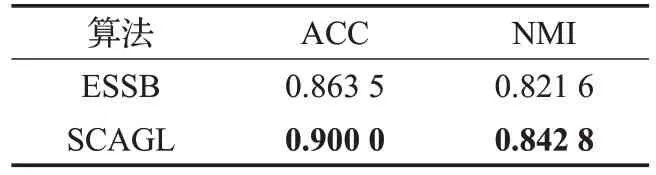
表6 在多視圖數據集上的ACC和NMI

只能在單視圖數據集上進行實驗的算法SSC、LRR、LSR、SGB 和k-means 在 mfeat 數據集的每個視圖上進行實驗，然后取平均值作為聚類準確率與歸一化互信息的值；ESSB、SCAGL直接進行實驗，實驗結果如圖1。

由圖1 可知，本文所提出的算法SCAGL 在多視圖數據集上比起其他聚類算法具有較好的聚類性能。

4.5 參數對算法性能的影響

本節選取ORL 數據集來進行實驗，研究算法中的不同參數以及視圖分割方式對聚類結果產生的影響。選取一個要研究的變量，固定其他參數不變，每次進行30次實驗，取平均值作為評判指標的值。本文研究的參數有分割率α、誤差項參數λ、圖正則化項參數β和算法迭代次數times。

4.5.1 分割率的影響

在本實驗中采用順序分割（Original）和隨機分割（Random）兩種分割方式，對分割率α分別取[0.5，0.25，0.2，0.1，0.05，0.025，0.02，0.01]來進行實驗。目的是對比不同的分割方式與不同的分割率對算法性能的影響。該實驗使用的其他參數一致，誤差項參數λ=8、圖正則化項參數β=0.02、算法迭代次數times=60。實驗結果為圖2。

由圖2 可知，一般情況下，順序分割的性能比隨機分割的性能好。當分割率α=0.05 時，順序分割方法的聚類效果達到最優；當分割率α=0.1 時，隨機分割方法的聚類效果達到最優。當分割率小于某個臨界值后，聚類準確率和互信息的值迅速下降，聚類效果越來越差，由此可見，并不是分割的視圖越多越好。

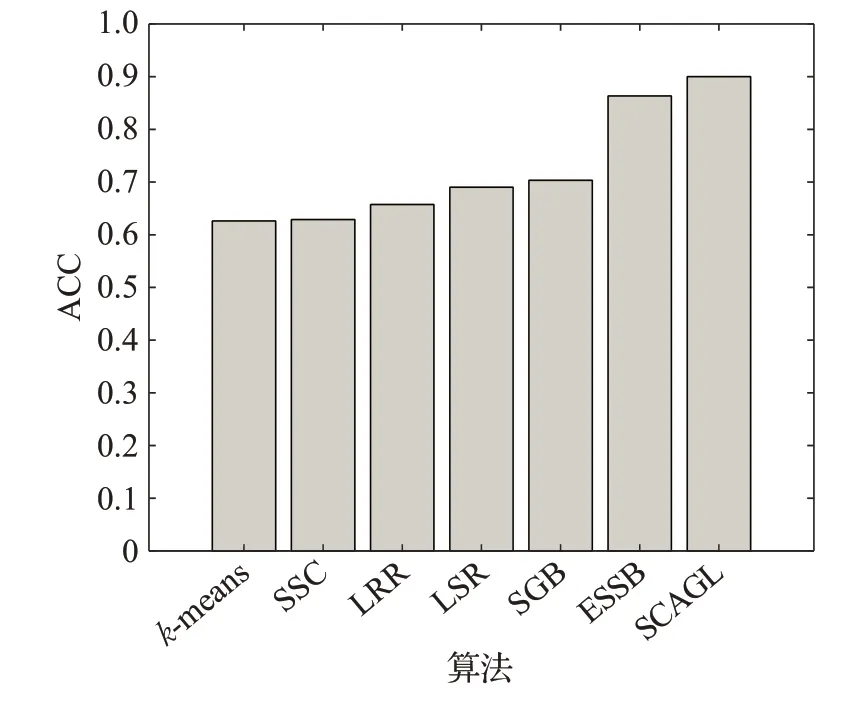
圖1 （a） 不同算法的準確率（ACC）

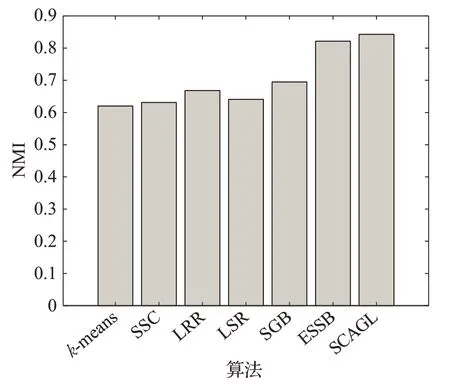
圖1 （b） 不同算法的歸一化互信息（NMI）

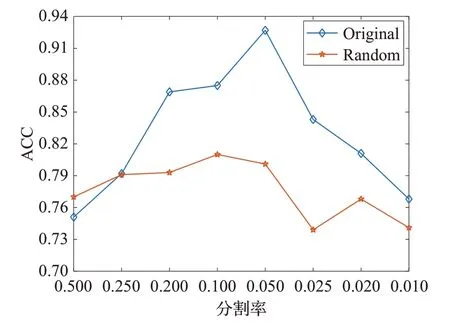
圖2 （a） 不同分割率對算法性能ACC影響

圖2 （b）不同分割率對算法性能NMI的影響

4.5.2 誤差項與正則化項參數

在本實驗中采取的分割方式為順序分割，設置誤差項參數λ以步長為2 在[2，22]的范圍內變化，圖正則化項參數β以步長為0.02在[0.02，0.1]的范圍內變化。目的是研究誤差項參數λ與正則化項參數β對算法性能的影響。實驗中其他參數不變，設置分割率α=0.2、算法迭代次數times=50。

由圖3可知，當誤差項參數λ=12，圖正則化項參數β=0.1 時算法的聚類性能最好，聚類準確率ACC 與歸一化互信息NMI達到了最優，分別為0.905 3與0.877 6。

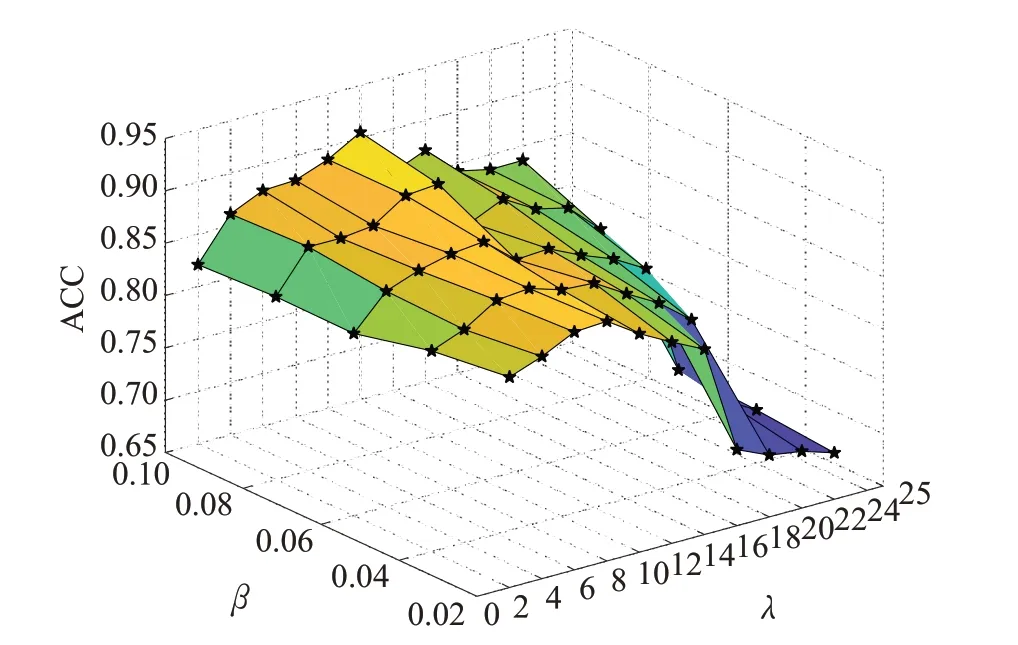
圖3 （a） 誤差項參數與正則化項參數對算法性能ACC影響

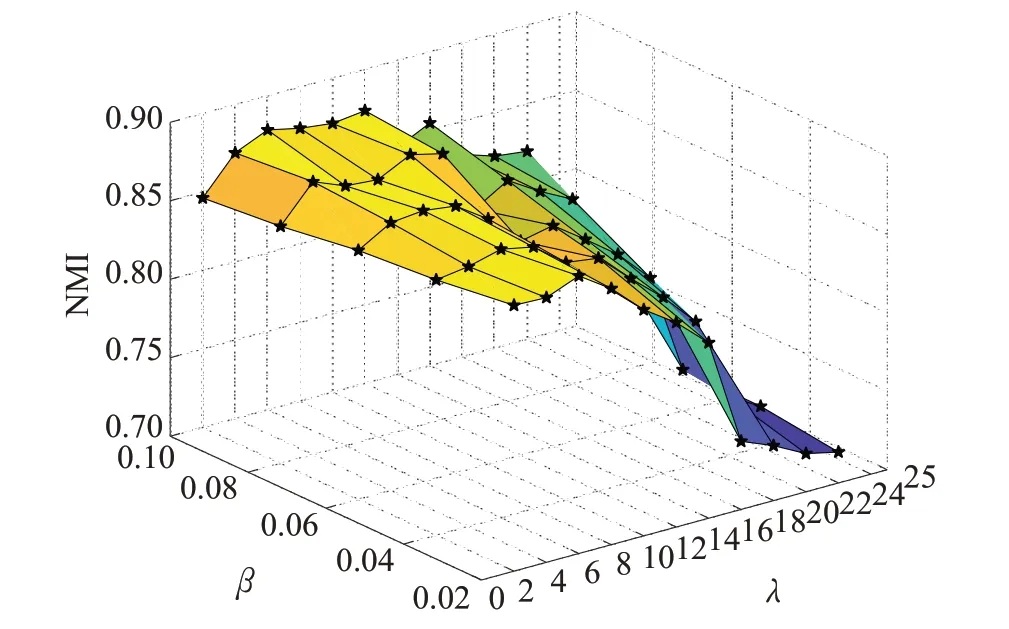
圖3 （b） 誤差項參數與正則化項參數對算法性能NMI影響

4.5.3 迭代次數的影響

本實驗中采用兩種分割方式順序分割（Original）和隨機分割（Random），對算法的迭代次數以步長10 在[20，120]的范圍內變化。目的是研究迭代次數對算法性能影響。其他參數設置為分割率α=0.2、誤差項參數λ=7、圖正則化項參數β=0.01。

由圖4可知當迭代次數達到50次時，算法性能比較好且趨于穩定，所以為了節約計算時間與計算成本，可以在實驗中設置迭代次數在50次左右。

圖4 （a） 迭代次數對算法性能ACC的影響

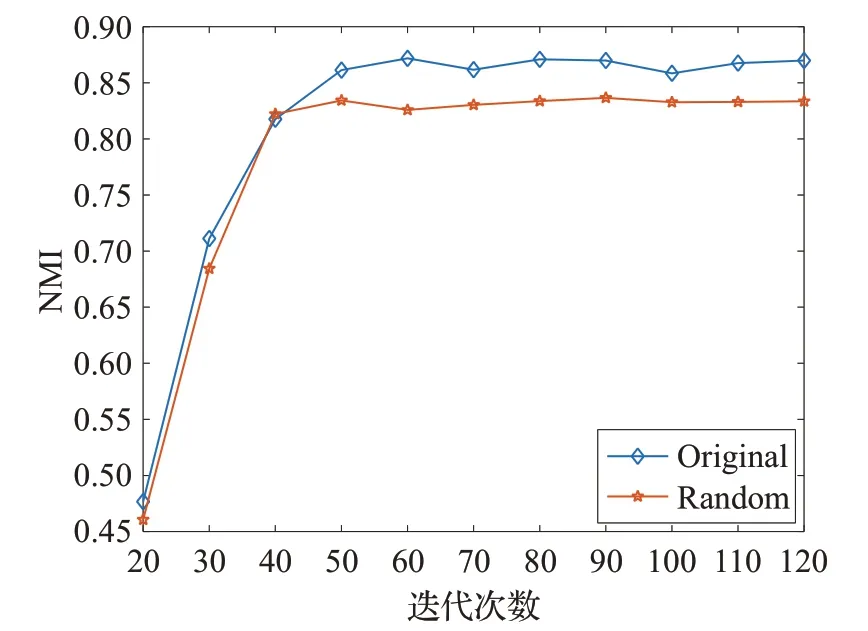
圖4 （b） 迭代次數對算法性能NMI的影響

5 結束語

基于譜分析的子空間聚類首先由數據構造關聯矩陣，再對關聯矩陣進行譜聚類。因此，聚類的效果依賴關聯矩陣的構造，本文提出了一種新的自適應圖學習誘導的子空間聚類算法。首先將單視圖數據多視圖化，受多視圖協同訓練思想的啟發，不同視圖間的信息具有一致性和互補性，因此可以利用不同視圖間的類簇信息，自適應地迭代更新每個視圖的圖正則化項，優化每個視圖的圖結構，得到聚類性能好的塊對角關聯矩陣，然后在關聯矩陣上進行譜聚類，將樣本聚到不同類簇中。進一步將本文算法與已有的聚類算法進行對比實驗，實驗結果顯示了該方法的優越性。