步長自適應追蹤法曲面求交技術的研究

劉 平 ，何雪明

1.江蘇省食品先進制造裝備技術重點實驗室，江蘇 無錫 214122

2.江南大學 機械工程學院，江蘇 無錫 214122

1 引言

在人工智能、數控加工、實體造型和科學可視化等方面曲面求交技術應用十分廣泛[1-2]。在基于逆向工程模型重建的過程中，高精度曲面求交是相鄰曲面成功拼接的前提，參數曲面間常用的求交方法[3]有網格離散法[4-5]、分割法[6-7]、迭代法和追蹤法[8]四種。其中網格離散法使用范圍較廣，通用性強，但求交過程中需要將整張曲面細密劃分，若曲面較大，計算耗時增加明顯；分割法是對網格離散法做出優化，將其求交過程中整張曲面的網格劃分轉變為僅對曲面間需要求交的部分進行劃分，求交時間顯著縮短。迭代法不能單使用，必須存在交點初值且該值必須盡可能的準確，初值選擇不恰當會導致收斂不及時從而無法得到滿足精度要求的交點，導致穩定性較差。追蹤法是已知一個交點的確切位置，將其作為追蹤起點，根據交線的幾何性質，按照一定的步長繼續搜索追蹤下一個交點，不斷重復這個的追蹤過程，直到追蹤到整條交線。相比其他方法進行曲面求交，追蹤法[9]是一種人們普遍認為曲面求交的有效方法，追蹤法的難點在于初始點獲取困難、容易漏交、不好確定合理追蹤步長。針對以上難點，國內外學者進行了大量研究。劉麗萍[10]采用包圍盒測試的方法，在分割法的基礎上得到了較為精確的初始點。史永豐[11]提出一種改進的基于微分方程的跟蹤算法，選擇邊界點和拐點作為跟蹤的起點，解決了漏交問題。涂海寧[12]采用拋物線逼近交線，求取拋物線滿足條件的最大弦長，并以此弦長作為追蹤步長求取交線，但此方法只適用于具有二階連續的曲面，適用受到限制。為了保證求交精度，一般最簡單的做法是取較小的固定步長值[9]，但計算量會顯著增加，導致計算速度變慢。

本文提出步長可自適應變化的優化追蹤法，不同于傳統的追蹤法，該方法采用五次非均勻B樣條曲線擬合交點，將步長與交線末端的曲率進行關聯，得到可依據實際求交的曲面特征而實時變化追蹤步長，適用范圍廣，求交穩定且速度快。

2 追蹤法的基本原理

2.1 確定追蹤起點

追蹤起點選取是追蹤法求交的第一步，求取初始交點首先需要將兩個參數曲面轉化成一組等參數曲線和一參數曲面[13]，把參數曲面間的求交問題轉化為容易求解的參數曲線與參數曲面求交的問題。計算跟蹤起點，現以一組曲面為例，如圖1所示。

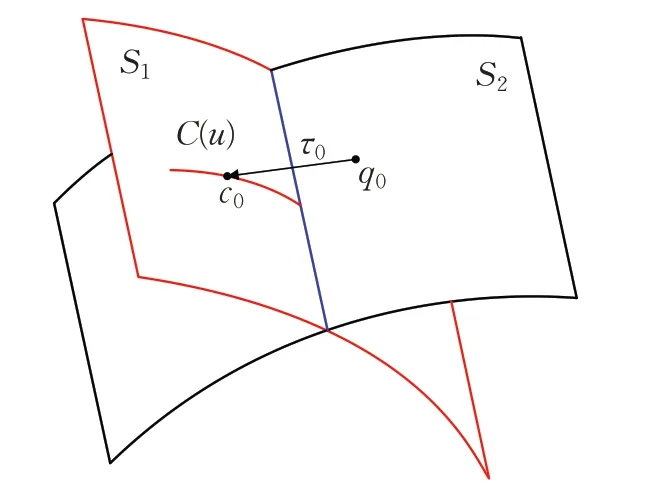
圖1 確定追蹤起點

在U、V方向上定義兩個參數曲面，分別為S1=S1(u1,v1)與S2=S1(u2,v2)。把曲面S1上的一條U向等參數曲線定義為C(u)，其方程可表示為C(u)=S1(u1,vˉ1)，其中參數vˉ1表示該參數是固定值。c0=S1(u10,vˉ1)是曲面S1等參數線C(u)上的一點，同時q0=S2(u20,v20)是參數曲面S2上的一點。將c0與q0之間的矢量距離表示為τ0=c0-q0，倘若設定一個精度閾值ε，當 |τ0|≤ε時，即兩個初始點之間的距離足夠小時，則認為兩曲面上的兩個點c0與q0重合，即為兩曲面的交點。

等參數線C(u)=S1(u1,vˉ1)的變量為u1，曲面S2對應的變量為u2和v2。求等參數線與曲面的交點，令：

對τ0=c0-q0用泰勒公式展開，忽略高次項可以得：

對上式進行賦范空間投影，在等式兩邊分別點乘S1u、S2u和S2v，則可以得到三個線性方程：

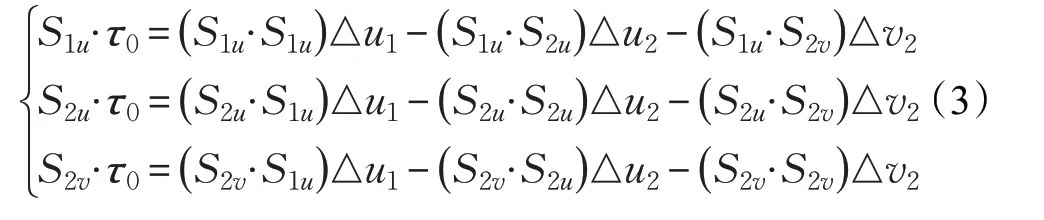
對方程組進行求解，可以求出△u1、△u2和△v2。此方程組由于系數矩陣正定，所以不會出現分母為0和不收斂的現象。將u10+△u1、u20+△u2和v20+△v2代入式（2）中，如此反復迭代計算，直到 |τ0|≤ε，則可以求得U向參數線C(u)與曲面S2的交點。通過對點c0采用泰勒公式展開，并依據賦范空間投影法進行迭代[14]。若C(u)和S2存在交點，c0將會在該交點處收斂。若C(u)和S2不存在交點，則點c0收斂于靠近S2距離最短的曲線C(u)上的一點，此時，尋找初始交點，應選取其余等參數線。

2.2 求取下一個交點

在求得初始交點后，接下來就要進行下一交點的求取，如此進行下去，就可以求得一系列交點，從而得到整條交線。進行下一個交點的求取，就必須知道該空間點的特征參數，需要對空間曲線上一點的幾何結構進行分析。

2.2.1 空間曲線在一點的幾何結構

了解空間曲線上一點的幾何結構，有利于精確下一個交點的位置。假設空間曲線c=c(s)為2 階參數連續曲線，c0=c(s0)是曲線c上的一點，s是弧長參數，則c0鄰近點可由泰勒公式展開表示為：

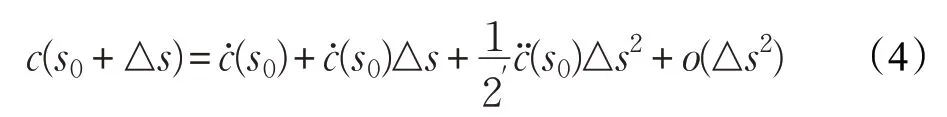
在微分幾何學中有：

其中，α、β和k為空間曲線c在點c0處的切矢、主法矢和曲率。依據切矢α和主法矢β可得到密切平面，記為Σ，進而得到空間曲線上點c0的幾何結構[15]，如圖2所示。

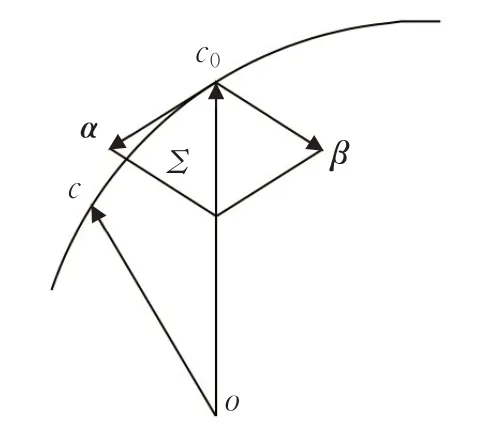
圖2 空間曲線上點的幾何特征

將式（5）代入（4）的表達式中，舍掉高次項，可以求出c(s0+Δs)的近似值，記作c′(s0+△s)：

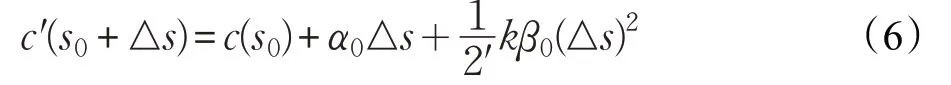
上面式子移項則等價于：

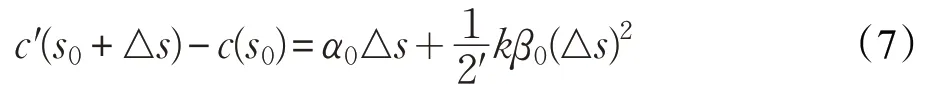
2.2.2 追蹤下一個交點

在密切平面Σ上，將c0作為原點建立正交坐標系，α和β矢量方向作為互相垂直的坐標軸。在坐標系[c0,α0,β0] 中，把c0定義為起點，則有：弧長參數s0=0 ；步長△s=s，相鄰點的坐標可表示為：

這樣，就可以在密切平面上的正交坐標系內分析曲線上某一點處的結構特征。從式（8）看出，計算c′(s)的值，需要求出追蹤步長s和等參數線上該點處的曲率k。

因為交線既在參數曲面S1中，也在參數曲面S2中，也因此可以借助兩個參數曲面的幾何特性間接獲得交線的特征。c0選定后，便可計算出兩個曲面在此點處的法矢，記為n1和n2，則相交線在點c0處的法平面就是法矢n1和n2組成的平面。相交線的切矢α垂直于法平面，可表示為：

因為交線主法矢β垂直于切矢方向，所以主法矢β一定處于由法矢n1和n2組成的法平面上。令曲率向量k=kβ=an1+bn2，取cos θ=n1·n2，兩曲面的法曲率記為，曲率方程兩邊分別乘以向量n1和n2，則：

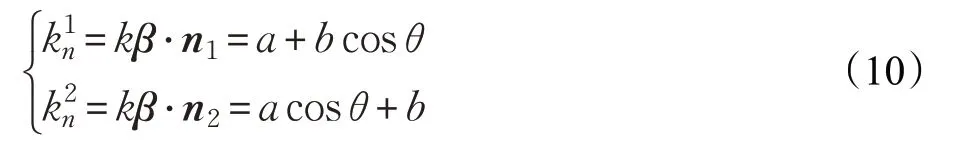
將a和b分別用表示，則：

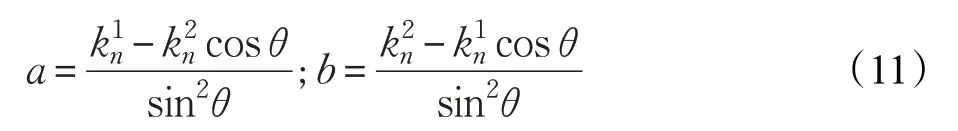
所以：

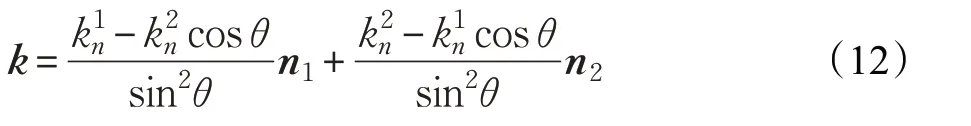
根據曲面的第一基本形式可得：

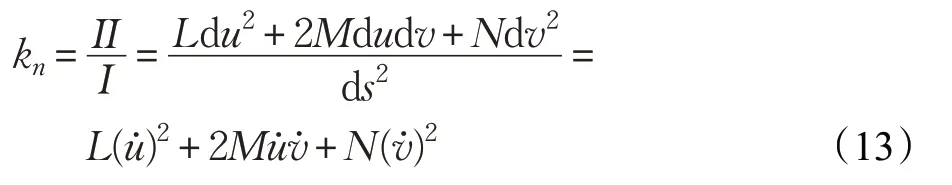
兩邊分別點乘Su和Sv，可以列出：

其中，E、F、G是曲面的第一類基本量。求解上式可以得到：

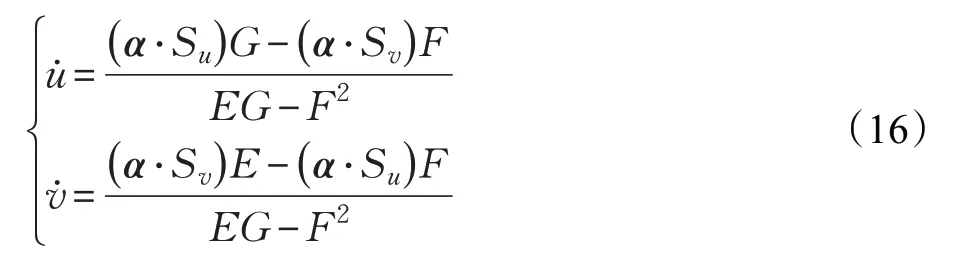
將式（16）代入式（13）中，可以求出曲面的法曲率。根據式（12），可以求出曲率向量k。根據曲率向量表達式可以求出主法矢β。曲線的曲率的大小為k的長度：

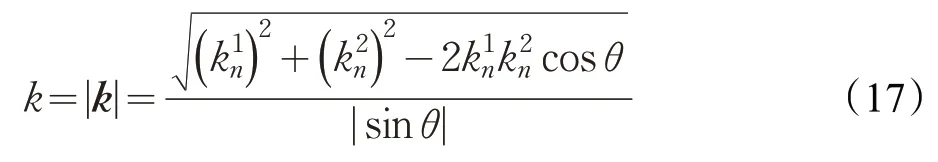
因此，可以分別求出曲率k、切矢α和主法矢β并和步長值s一起代入式（8）中，可求出下一個交點的近似位置。需要注意的是，想要得到該點的精確位置，還需要進一步迭代。

3 步長可自適應的追蹤法求交

設定合理的步長值，可以得到較準確的交線位置和較高的求交效率。傳統追蹤法追蹤步長都是固定值，步長大小根據經驗均是人為設定，在針對復雜曲面求交時不夠靈活方便，不夠穩定。基于步長自適應的追蹤法在求交過程中將追蹤步長與交線末端的曲率半徑相關聯，使步長可根據曲面真實特征實時變化。

3.1 確定初始插值點

節點矢量的分布可以決定B 樣條基函數的變化情況[16]。實驗發現插值曲線的階次為五次時，測量精度要高于三次和四次，而采用六次和七次曲線進行插值會產生振蕩現象，反而測量精度降低。根據節點的變化規律[17]，五次非均勻B 樣條曲率具有連續性，其擬合的曲線平滑且符合常規產品的曲面特性[18]，所以本文采用五次非均勻B樣條曲線擬合交線上的點。

3.2 計算曲線末端曲率

若將五次非均勻B 樣條曲線方程定義為C(u)，則C(u)的末端點即為參數u=1 時所對應的點，曲線的曲率計算公式為：

其中，C′(u)、C′(u)分別為曲線的一階、二階導數。當kr ＜0 時擬合曲線沿前進方向順時針彎曲；kr ＞0 時擬合曲線沿前進方向逆時針彎曲。曲線某點處的曲率半徑可表示為：

3.3 確定自適應追蹤步長s

值得注意的是：較小的追蹤步長可以提高求交精度，但同時計算量增加；較大的追蹤步長可以提高求交效率，但會影響求交精度，所以討論合理的自適應追蹤步長取值具有重要意義。

先按照固定步長求取六個交點，將六個點依次定義為Q0、Q1、Q2、Q3、Q4、Q5，然后采用五次非均勻B樣條進行擬合。將固定追蹤步長求取的六個交點插值為五次非均勻B 樣條曲線后，如圖3 所示，在曲線末端點Qp處以曲率半徑r，構造該點處的曲率圓O1，連接O1Qp，給定一個跨距角θ，得到圓上的一點Qp+1，即為下一個追蹤點，弦長QpQp+1即為跨距S，也就是自適應追蹤步長值。確定自適應步長S的值后，也就確定了下一個追蹤點Qp+1的大致位置。

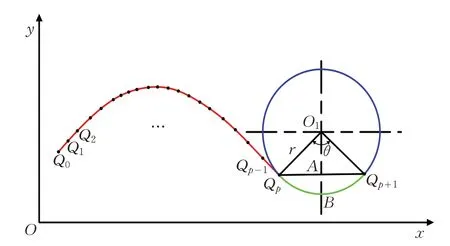
圖3 確定自適應步長原理圖

AB為圓弧QpQp+1與弦QpQp+1的最大距離，當圓弧QpQp+1上的點到弦QpQp+1上的距離不超過閾值e，即AB＜e時，可以用弦QpQp+1來近似表示圓弧QpQp+1，如下方程所示：

當θ=2×arccos(1-e×kr) 時 ，交 線 上 的 點 到 弦QpQp+1的距離為最大值e。根據上式可知，曲率kr越小，θ的值同時也會越小，AB值越大，自適應追蹤步長的值就會越大；反之，當曲率kr越大時，θ值就越大，AB值越小，自適應追蹤步長值就會越小。其中e的大小由測量精度要求決定，精度要求越高，e的值就越小，求交得到交點的數量就越多，一般取精度閾值e=0.01 mm。如圖3所示，把自適應追蹤步長S表示為：

確定曲率kr，即基本確定了自適應步長S的值。

3.4 基于自適應追蹤步長曲面求交過程

需要注意的是根據自適應步長確定的下一個追蹤點，得到的曲面交點位置并不精確，需要采用迭代法求出該交點的精確位置[19]。首先，分別在兩參數曲面S1和S2上選取距點c′(s)較近的兩個點，分別記為p1和p2，p1屬于參數曲面S1，p2屬于參數曲面S2。若有p1和p2收斂于鄰近點c(s)，則該點符合設定的精度要求：|p1-p2|≤ε。若p1和p2在鄰近點處無法收斂，則將p2定義為交點的近似點，不斷重復上述的計算過程。然后以迭代求取的精確點c(s)作為初始交點，繼續計取下一個交點的位置，直至追蹤到參數曲面的邊界。追蹤步長可自適應曲面求交過程的算法流程，如圖4所示。

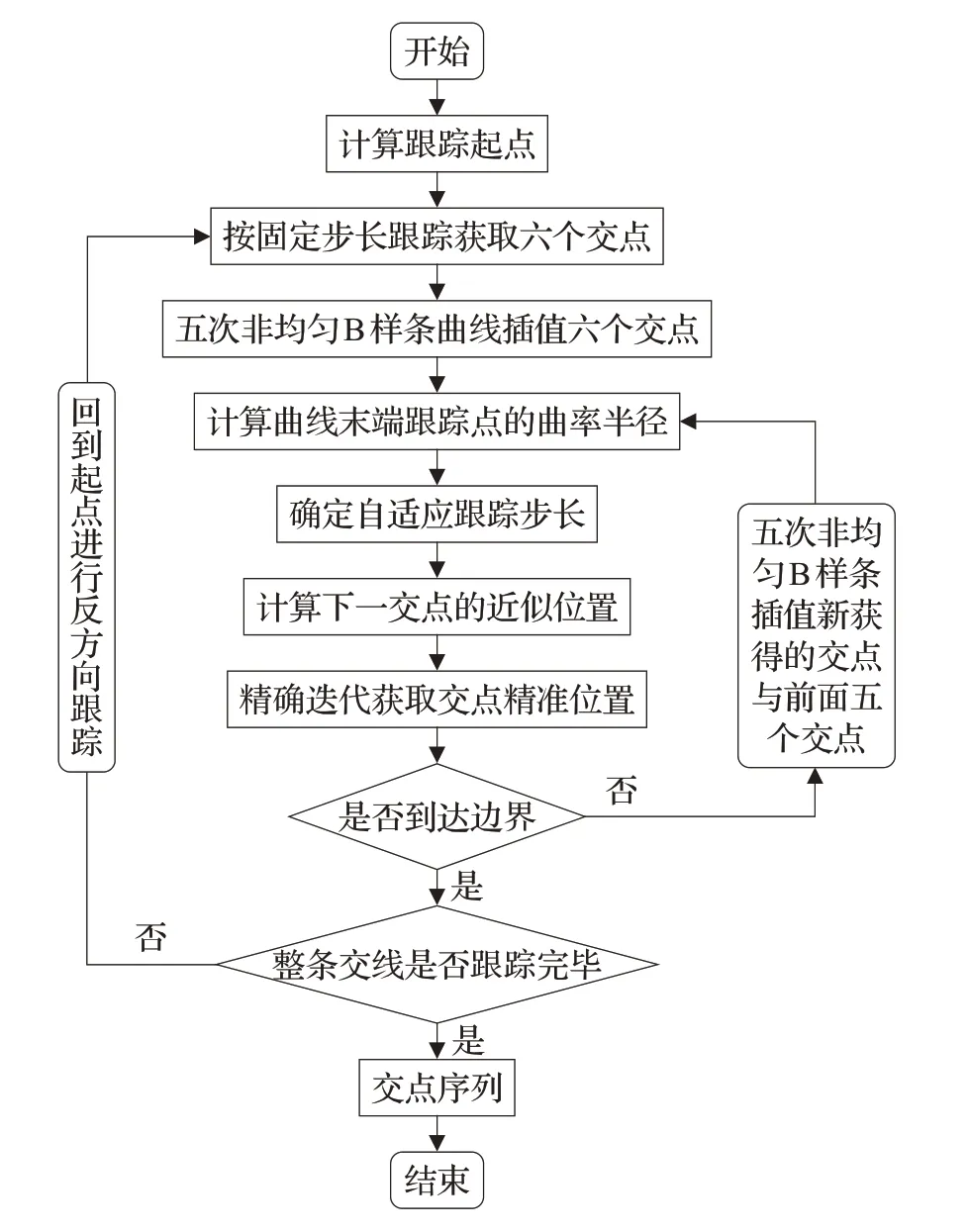
圖4 追蹤步長可自適應曲面求交過程

4 實例驗證

為驗證基于步長自適應追蹤法求交相比傳統追蹤法求交的優越性性，提出對具有不同特征的曲面進行多組求交實驗。將曲面在步長自適應和固定步長兩種方式下進行求交，對比求交結果。需要說明的是：為方便求交結果的對比，以下所有求交試驗均設置交點精度閾值ε為0.001 mm。

4.1 平面和自由曲面求交

為了驗證五次非均勻B 樣條曲線曲率連續自適應步長跟蹤求交算法的可行性，結合C++面向對象開發語言和OpenGL 等圖像數學函數，以平面與曲面、曲面與曲面求交為例，對曲面求交進行可視化。

如圖5所示，為兩個在逆向系統軟件中重構出來的相交曲面，根據重構點云獲取曲面邊界信息，如圖6 所示，曲面的U向跨距為12 mm，V向跨距為34.05 mm；平面的U向跨距為12 mm，V向跨距為32.1 mm。根據曲面邊界信息，設置曲面U向、V向等參數線數量，如圖7 所示，跟蹤步長選擇為自適應步長，精度閾值設為0.001 mm。求交結果如圖8所示，藍色的曲線即為平面與曲面的交線。

圖5 平面與曲面相交模型

圖7 跟蹤步長設置

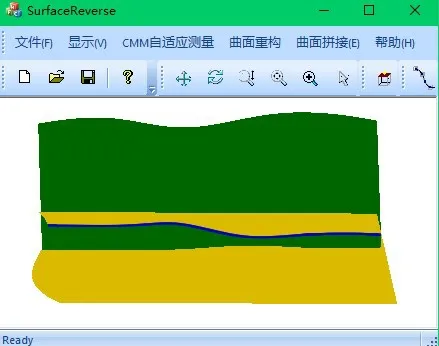
圖8 平面與曲面求交結果

4.2 兩個自由曲面間求交

平面與曲面求交實驗驗證了該求交方法的可行性，為了進一步驗證該求交方法的通用性，選取更具代表性的自由曲面進行求交實驗，如圖9所示。與平面和自由曲面求交參數設置一樣，先根據曲面邊界信息設置等參數線數量，然后設置步長和精度閾值，這里依然選用的自適應步長，精度閾值設為0.001 mm，求交結果如圖10 所示，結果驗證了自由曲面與自由曲面求交的可行性。

通過平面與曲面求交、曲面與曲面求交實驗驗證了自適應求交算法的可行性后，為了進一步驗證該求交算法的可靠性以及優越性，將自適應步長求交算法與固定步長求交算進行對比，并對其求交誤差和求交速度進行分析。

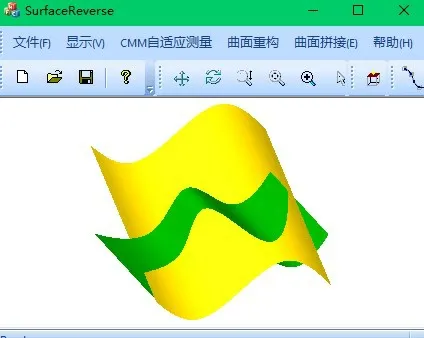
圖9 自由曲面相交模型

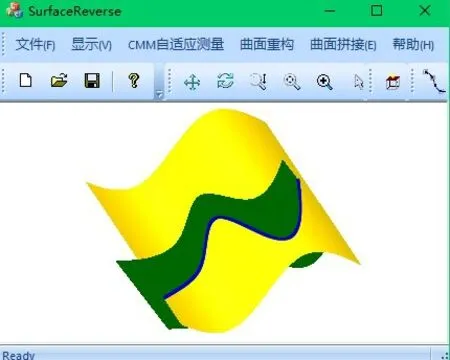
圖10 自由曲面求交結果

實驗分別以自適應步長、固定步長3 mm、5 mm、10 mm、15 mm 以及 20 mm 進行對如圖9 所示的兩自由曲面進行求交實驗，求取不同步長下的交線，交線求取結果如圖11 所示，從圖中可以看出，當步長不斷增大時，所求得的交線與實際交線偏移量越大，求交誤差不斷增加。

圖11 不同步長求交結果

為了更好地反映誤差與跟蹤步長之間的變化關系，在imageware 軟件中對誤差進行了量化，分別繪制了自適應步長以及不同固定步長所求交線的誤差云圖，如圖12所示。

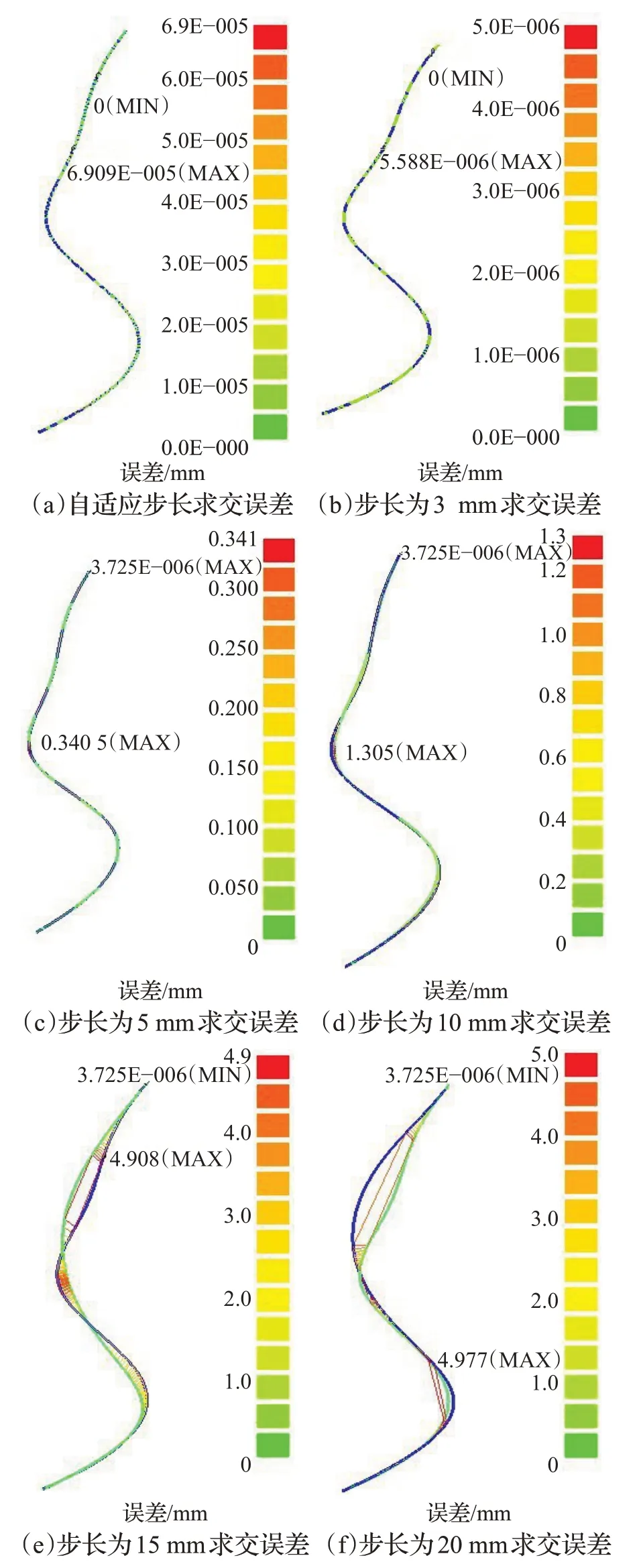
圖12 不同步長曲面求交誤差

圖12 中藍色線條表示所求交線，其他顏色線條用來反應所求交線與實際交線的偏離程度，其中最大偏離誤差用MAX表示，最小偏離誤差用MIN表示。可以看出，在曲線曲率較大的地方，誤差明顯增大。為了更直觀地展現誤差與跟蹤步長之間的關系，量化誤差。將誤差進行數據統計得到表1。

從表1 可以看出，跟蹤步長為3 mm 時交線的最大誤差為5.588E-06 mm，最小誤差為0 mm，平均誤差為2.79E-06 mm，求交精度高；步長為5 mm 時，最大誤差為0.340 5 mm，最小誤差為3.725E-06 mm，平均誤差為0.170 mm，求交精度一般；當步長為10、15、20 mm，平均誤差為毫米級，求交誤差較大，無法達到精度要求；采用自適應步長時，交線的最大誤差為6.909E-05 mm，最小誤差為0 mm，平均誤差為3.45E-05，與步長為3 mm 時求交的精度接近，但是計算次數比步長為3 mm 時減少了43%左右，計算量減幅較大，計算量較小；與步長為5 mm時的求交相比，計算次數基本一致，計算量基本相同，但精度高出4個數量級。

表1 多種步長下的交線誤差

4.3 圓錐面與圓柱面間求交

找到含有規則曲面的實物，如圖13所示，利用實驗室已有設備CMM 對實物中標記的兩個曲面進行點云采集。

圖13 含有規則曲面的實物

將采集到的點云數據在SurfaceReverse 中顯示，如圖14所示。并進行曲面重構延伸相交，如圖15所示。

圖14 點云數據

圖15 重構曲面延伸相交

設定精度閾值ε=0.001 mm，步長值取5 mm、14 mm及自適應步長，求交結果如圖16所示。

為了更好地反映誤差與追蹤步長之間的變化關系，將自主研發的逆向系統SurfaceReverse 求取的交線與UG NX 求取的交線進行對比分析，將誤差數據制作成表2。

從表2 可以看出，自適應追蹤步長求得交點數為48，相比追蹤步長為5 mm時計算次數減少了36.8%，但是兩者誤差相差不大，精度在同一個量級，均符合要求；步長為14 mm的曲面相交誤差比較大，超過了誤差許可范圍。

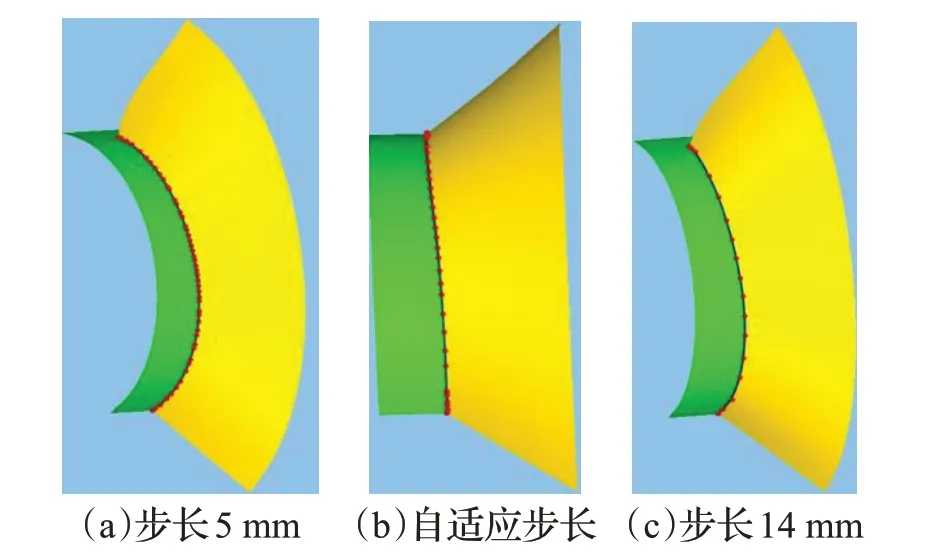
圖16 取不同步長值下的曲面求交結果

表2 不同追蹤步長下的交線誤差

通過對表1、表2的數據進行分析可以發現，對于傳統追蹤法求交，追蹤步長越小，計算次數會顯著增加，求取的交點數也會越多，計算量增多，求取交線的效率會降低很多，但求取的交線精度很高。相比之下，步長可自適應變化的追蹤法求交，在滿足同等求交精度的情況下，依舊可以保持較高的求交效率。結果表明：這種相交算法速度較快。

5 結論

（1）在求交過程中將追蹤步長與交線末端的曲率半徑相關聯，得到可自適應變化的追蹤步長。對具有不同特征的復雜曲面在步長自適應方式下進行求交試驗，結果表明，在同一個誤差許可范圍內，相比傳統的固定步長追蹤方法，采用步長可自適應變化的追蹤法進行曲面求交的交線平均誤差均μm級，求交誤差小，精度高。

（2）對同一組曲面在步長自適應和固定步長兩種方式下進行求交試驗，對比發現，固定步長過小，精度可明顯提高，但計算量過大，耗時增加；固定步長過大，誤差明顯增加，得到結果不夠精確。試驗結果表明，基于步長自適應的追蹤法求取到的交點不僅能隨曲面特征合理分布而且具有更高求交效率。