Singer模型算法在目標跟蹤中的應用研究
房曉麗 陳玉敏 方鑫鈺

摘要:近些年來,導彈跟蹤制導對雷達機動目標的精確跟蹤提出了前所未有的挑戰,如何實現雜波環境下機動目標的精確跟蹤一直是個難點。文章建立了雜波環境下機動目標Singer運動模型,給出了濾波方程,仿真分析了基于Singer模型的機動目標跟蹤效果和精度。仿真結果表明,Singer模型對機動目標跟蹤具有較好的跟蹤效果。
關鍵詞:Singer模型;濾波;機動目標跟蹤
中圖分類號:TP311
文獻標識碼:A
文章編號:1009-3044(2020)27-0007-04
開放科學(資源服務)標識碼(OSID):
1 背景
機動目標跟蹤作為國防領域中的彈道導彈精確制導的關鍵技術,具有重要的研究前景。它在衛星及導彈防御系統、火力控制、跟蹤與攻擊、戰場監視等方面均可發揮重大作用[1]。在民用方面,機動目標跟蹤也發揮著舉足輕重的作用,它主要應用于空中交通管制、航海及航空中的導航、機器人的道路規劃等。
對機動目標跟蹤效果的評估主要是通過建立機動目標動力學模型來實現的[2]。然而,由于機動目標在飛行或航行時經常會突然出現轉向、變速等運動,具有很強的隨機性、突發性,導致建立機動目標模型需要考慮的因素很多,準確建模相對困難。
目前,建立機動目標動力學模型的算法很多,主要有變維VD模型算法、輸入估計IE算法、Singer模型算法以及以交互多模模型為主的多模型跟蹤算法等[3-4]。本文采用Matlab仿真分析方法,基于Singer運動模型,在同一仿真戰情下分析了機動目標的跟蹤效果和跟蹤精度。
2 Singer算法描述
假定目標進行平面運動,其運動方程可以描述為:
X(t)=FX(t)+Ga(t) (1)
其中,a(t)為目標的加速度。對于跟蹤系統,目標的機動性不可知,所以顯而易見準確可靠地描述目標加速度是一個核心問題,smger算法把加速度a(t)看作一個平穩隨機過程[5],其自相關函數為:真程序,利用蒙特卡羅方法對跟蹤濾波器進行仿真分析[9-10],假定測試次數為50次,值得注意的是這里的次數假定,因為假定T的值為10s,測試次數即踩點次數為總時間除以T,所以為了滿足條件我們選擇了始終的50次。為了清晰觀察目標的真實軌跡、測量軌跡以及濾波軌跡分別見圖1至圖4所示。
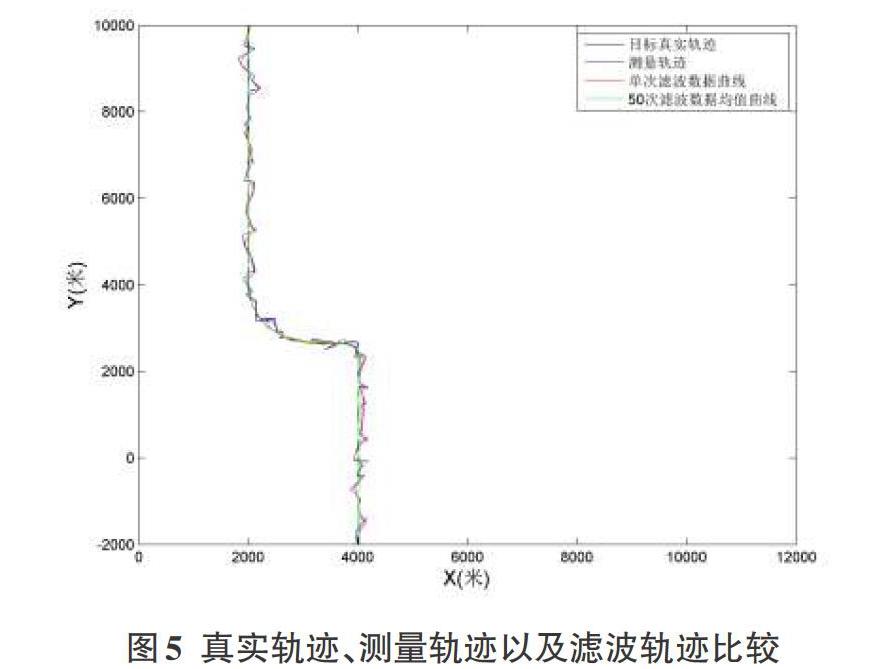
為了方便比較,把四條軌跡線繪制在一個圖5中。可以看出,單次濾波曲線效果不是很理想,軌跡仍然有很大的波動,但是采用蒙特卡羅方法后[11],通過多次觀測取均值,濾波效果較好。
同時,不難發現在目標勻加速過程中,Singer算法可以有效跟蹤目標[12-13];在目標加速過程中,Singer算法跟蹤效果并不是很好,特別是在加速度比較大時,比如該例子中的第二個轉彎時,跟蹤效果不理想。
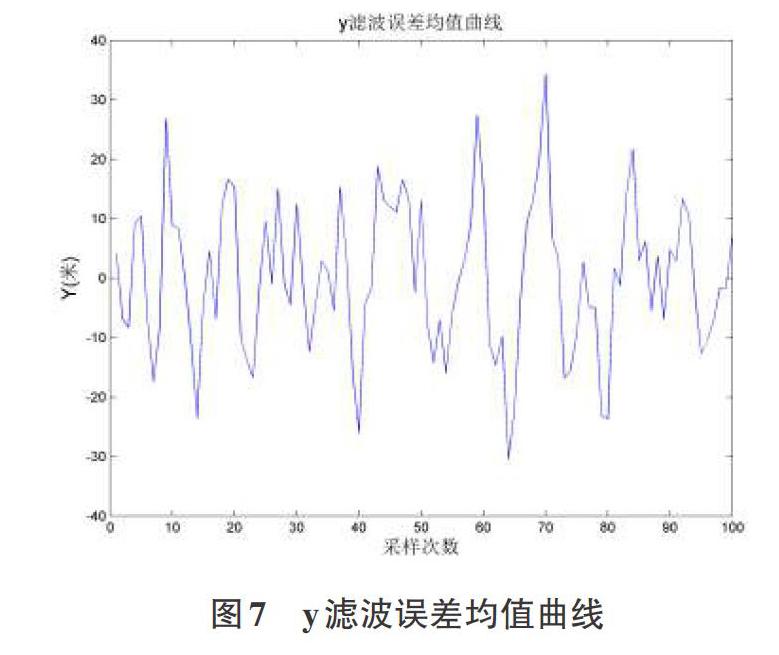
此外,X方向,Y方向濾波估計誤差均值及誤差標準差見實驗圖6至圖9所示。由圖并不能看出目標運動的特點,這也說明Singer算法雖然在多次濾波取均值的情況下效果較好,但是仍然有一定的局限性[14],誤差比較大。
還可看出,圖6和圖7中在第二個轉彎處相對較大的峰值體現了Singer算法對目標加速度較大過程中的跟蹤效果不理想;而在勻速以及加速度較小時可以較好地跟蹤目標,這跟圖5中從軌跡中得出的結論是一致的。圖8、圖9可以看出,誤差的標準差較大,誤差起伏較大,說明該算法還具有一定的局限性。
5 結束語
本文從理論上推導了雜波條件下機動目標的Singer模型相關矩陣,從仿真方面分析了其相關特性。Singer算法模型在勻速或者加速度較小條件下可以良好的跟蹤機動目標,在目標實施轉彎,即加速度較大時跟蹤效果一般,因此該方法在追蹤轉彎運動頻繁的目標時有一定的局限性。
參考文獻:
[1] Singer R A.Estimating optimal tracking filter performance formanned maneuvering targets[J]. IEEE Transactions on Aero-space and Electronic Systems, 1970, AES-6(4): 473-483.
[2]韓偉,黃曉斌,張燕.Singer模型下α-β-γ濾波的信息序列特性分析[J].計算機工程與應用,2013, 49(3): 156-158, 233.
[3]戚靖,劉成成,郭偉龍,等.一類基于改進的當前統計模型的目標跟蹤算法研究[J].上海航天,2014, 31(2): 52-56.
[4]譚順成,王國宏,王娜.lMM-Singer模型的機動目標跟蹤算法[J].火力與指揮控制,2012, 37(2): 32-34.
[5]吳偉,王東進,陳衛東,密集雜波環境下多目標跟蹤算法[J].現代雷達,2007, 29(2): 17-21,31.
[6]魏喜慶,顧龍飛,李瑞康,等.基于Singer模型的高超聲速飛行器軌跡跟蹤與預測[J].航天控制,2017, 35(4): 62-66, 72.
[7]張燕,柳超,李云鵬.基于改進Singer模型的機動目標跟蹤方法[J].火控雷達技術,2015, 44(3): 37-40, 50.
[8] Geng Y R,Wang J L.Adaptive estimation of multiple fadingfactors in Kalman filter for navigation applications[J]. GPS So-lutions, 2008, 12(4): 273-279.
[9] LiX R,Jdkov V P.Survey of maneuvering target tracking.PartI. Dynamic models[J]. IEEE Transactions on Aerospace andElectronic Systems, 2003, 39(4): 1333-1364.
[10] Liu H Z,Tongue B H.Indirect spacecraft trajectory optimiza-tion using modified equinoctial elements[Jl. Journal of Guid-ance, Control,and Dynamics, 2010, 33(2): 619-623.
[11] Jia S Y.Research Institute of Information Fusion Naval Aero-nautical and Astronautical University Yantai China, Zhang Y,et al.Highly maneuvering target tracking using multi-parame-ter fusion singer modeI[J]. Journal of Systems Engineering andElectronics, 2017, 28(5): 841-850.
[12] Wu W, Pan Q,Zhao C H,et al.A probability hypothesis den-sity filter with Singer model for maneuver target tracking[Cy/Proceedings of the 32nd Chinese Control Conference. 26-28July 2013, Xi'an, China.IEEE, 2013: 4778-4782.
[13] Lee Y L,Chen Y W. IMM estimator based on fuzzy weightedinput estimation for tracking a maneuvermg target[Jl. AppliedMathematical Modelling, 2015, 39(19): 5791-5802.
[14] Zhu L H,Cheng X H.High manoeuvre target tracking in co-ordinated turns[J]. lET Radar, Sonar&Navigation, 2015, 9(8):1078-1087.
【通聯編輯:謝媛媛】
作者簡介:房曉麗(1985-),女,山東壽光人,講師,碩士,主要研究方向為信號與信息處理、衛星導航定位等。

