基于模式集成的松花江流域氣候模擬預估

劉智天，郝振純，徐海卿，鞠 琴，武冠一，邢若飛

(1.河海大學水文水資源與水利工程科學國家重點實驗室，江蘇 南京 210098；2.河海大學全球變化與水循環國際合作聯合實驗室，江蘇 南京 210098；3.中國水利水電科學研究院，北京 100038；4.中國市政工程華北設計研究總院有限公司，天津 300000)

0 引 言

全球范圍的劇烈氣候變化，對人與自然環境產生了很大影響，這一影響加劇了水循環過程，直接影響降水、蒸發、徑流等氣候因子，導致水資源時空上的再分配，使極端氣候事件發生的概率上升[1]。自20世紀80年代起，全球氣候變化逐漸演變為一個應用多學科的新研究領域，尤其是氣候變化對水資源的影響，成為當今大氣學和水文學界的重要課題。政府間氣候變化專門委員會IPCC成立于20世紀80年代末，集中了世界多國的科學家共同探討氣候變化帶來的影響。2013年發布的第5次研究報告指出：人類活動主導了20世紀50年代以來的全球變暖，可能性不低于95%。氣候的暖化十分肯定，全球范圍海陸表面平均溫度在1880年～2012年呈上升趨勢，2003年～2012年平均溫度比1850年～1900年高約0.78 ℃。過去的近30年很有可能是史上最熱時期[2]。

為此，國內外開展了很多利用模式數據和實測資料分析水文要素時空分布及演變趨勢的研究[3-7]。本文以松花江流域為研究對象，所用模式參考不同GCMs在我國的模擬表現[8-13]，模式降尺度后應用多種集成方法提升模擬性能，預估在RCP4.5氣候情景下降水、氣溫及徑流未來可能的變化。

1 數據和方法

1.1 研究區概況

松花江流域位于41°42′～51°48′N，119°52′～132°31′E，東西長920 km，南北寬1 070 km，全部在中國境內。北源嫩江發源于大興安嶺伊勒呼里山，河源高程1 030 m，全長1 370 km，流域面積29.85萬km2，河流由北向南流；南源第二松花江發源于長白山脈主峰白頭山，河源海拔2 744 m，全長958 km，流域面積7.34萬km2，河流從東南流向西北。嫩江與第二松花江在黑龍江省肇源縣三岔河處匯合后，折向東北稱為松花江干流，在同江市匯入黑龍江，全長939 km，流域面積56.12萬km2。

1.2 數據資料

CMIP5模式通過敏感性分析檢測氣候變化和歸因，模擬歷史數據并開發代表性濃度路徑的氣候情景，引入未來氣候變化的預估實驗[14]，提升參數的處理能力及空間分辨率，將動態植被與碳循環模式引入部分模式[15]。本文所用模式(見表1)的歷史模擬區間為1951年～2000年，預估未來區間為2020年～2099年。

表1 CMIP5模式信息

實測氣候要素資料源于中國氣象數據網(http:∥data.cma.cn)，選擇松花江流域內氣象站同期觀測的降水和氣溫逐月數據，和模式模擬數據做比較分析。

1.3 集成方法

1.3.1算數平均集成

方法簡單，結果較穩定，計算公式為

(1)

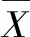
σ=Pa/Psea

(2)

Ps(t)=Pse(t)×σ

(3)

式中，Ps(t)為降水算術平均值；Pse(t)為率定期序列值；Pa為降水率定期實測均值；Psea為Pst(t)的均值。

Ts=Ta-Tsea

(4)

Ts(t)=Tse(t)+Ts

(5)

式中，Ts(t)為氣溫算術平均值；Tse(t)為率定期序列值；Ta為氣溫率定期實測均值；Tsea為Tse(t)均值。

1.3.2權重平均集成

權重系數αi計算公式為

(6)

(7)

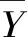
(8)

式中，Ye(t)為權重平均值；Yi(t)為模式i在t時刻的模擬值；αi為權重系數。

1.3.3多元回歸集成

建立回歸方程表征變量間的函數關系，誤差允許范圍內得出的關系式可認為合理。高階微分非線性多元函數F=f(x1，x2，…，xn)用多項式逼近，各乘積項為自變量[17]。模擬值為自變量Zi，實測值為因變量Z。即

(9)

式中，bi為回歸系數；e為隨機誤差項。

1.3.4BP神經網絡集成

BP神經網絡是通過大面積神經元豐富完善連接的非線性動態系統[18]，進行大型計算和數據貯存，逐漸成為解決不同領域復雜問題的方法[19]。結構分為輸入層、隱含層和輸出層，隱含層的節點為隱節點，樣本值向下傳遞到隱含層后通過權重系數和函數算法變成隱節點再傳遞，在輸出節點計算輸出值和樣本檢驗值的誤差，通過輸出層向輸入層反向計算得到最終輸出值。模式模擬值為輸入層，實測值為輸出層。隱含節點數通過經驗公式計算，即

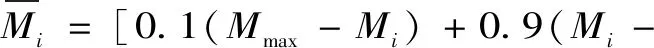
(10)

2 結果分析

2.1 氣候模式性能評估

松花江流域歷史實測多年平均降水為531.99 mm，平均氣溫為1.77 ℃。圖1為模式模擬歷史降水氣溫與實測資料的比較。

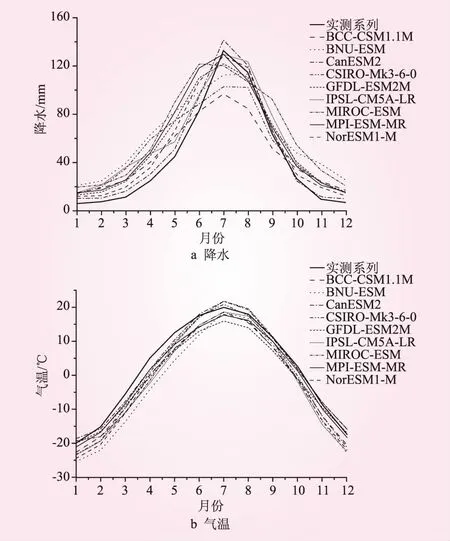
圖1 CMIP5模擬和實測比較

2.1.1降水

表2為模式模擬降水和實測的比較結果。

由圖1a知，所有模式整體變化趨勢保持一致，降水實際較少時模擬值通常偏大，而實際降水較多時多數模擬一般偏小，局部模式存有個性。從表2知，多數模式模擬降水的平均相對誤差低于30%，相關系數基本都超過0.8，且大部分確定性系數不低于0.6。這說明模擬結果和實際的吻合程度較好。

綜合模擬和實測的比較結果，認為CanESM2和NorESM1-M模擬降水較好。

2.1.2氣溫

表3為模式模擬氣溫和實測的比較結果。

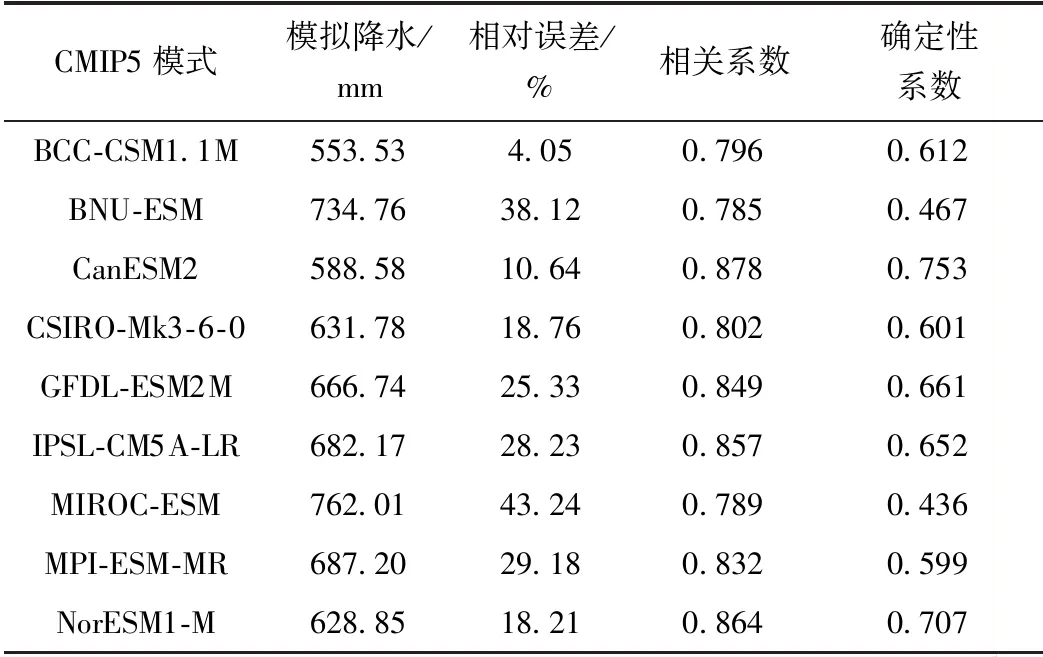
表2 降水CMIP5模擬和實測比較

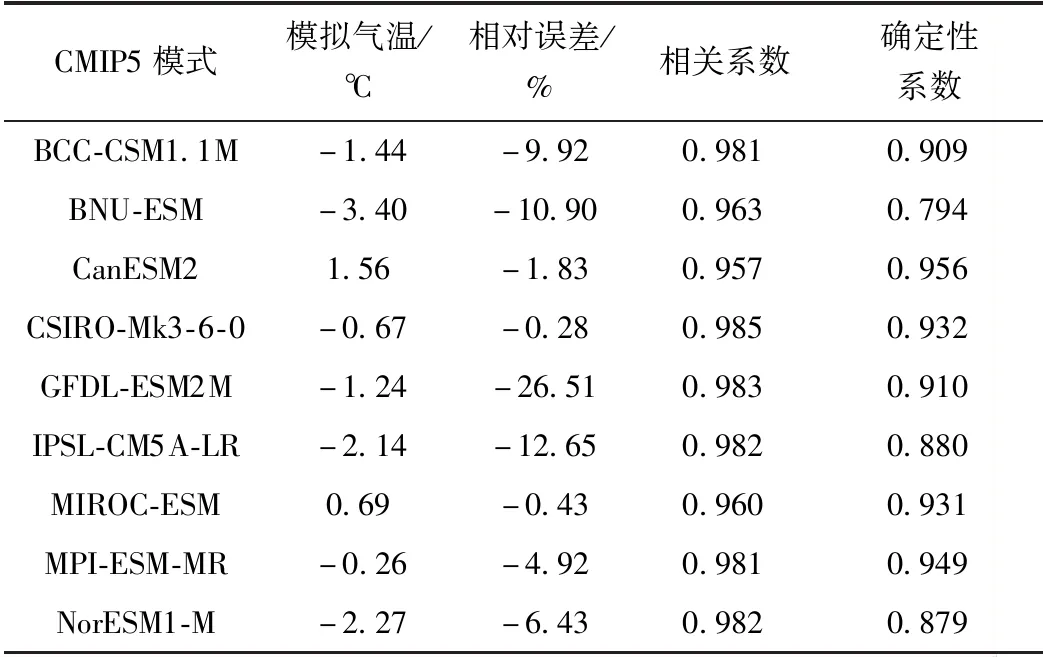
表3 氣溫CMIP5模擬和實測比較

由圖1b可知，氣候模式模擬氣溫整體精度較高，模擬氣溫的年內平均變化和實際趨勢相同。從表3可知，模擬氣溫的平均相對誤差都較低，多數模式低于10%，相關系數均超過0.95，大部分模式確定性系數超過0.9，和實際的吻合程度較高。

比較模擬結果認為，CanESM2和MPI-ESM-MR模式模擬氣溫較好。

考慮模式同時模擬降水和氣溫的結果，最終認為CanESM2和MPI-ESM-MR模擬良好。

2.2 模式集成性能評估

2.2.1降水

所用模式通過σ方法降尺度后進行多模式集成的模擬計算。歷史模擬數據率定期為1951年～1995年，檢驗期為1996年～2000年。集成方法和優選模式模擬降水的比較結果見表4。

從表4可知，集成方法在率定期和檢驗期的評價指標結果要比單個模式好，削弱了個性因素使模擬更加穩定。集成模擬的降水時間序列更貼近于實測資料，降低了單個模式模擬結果的不確定性，評價趨于均值化。比較集成方法的模擬結果，認為多元回歸集成和BP網絡集成模擬降水較好。

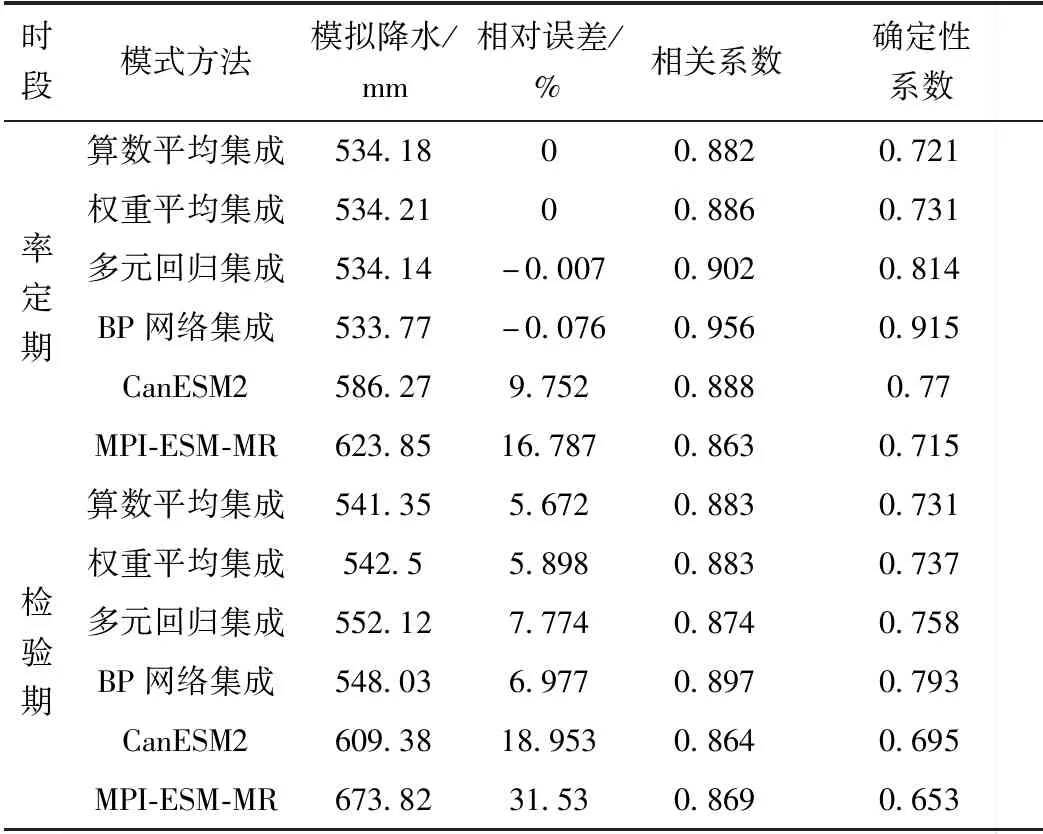
表4 降水模擬結果比較

2.2.2氣溫

各方法模擬氣溫的比較結果見表5。

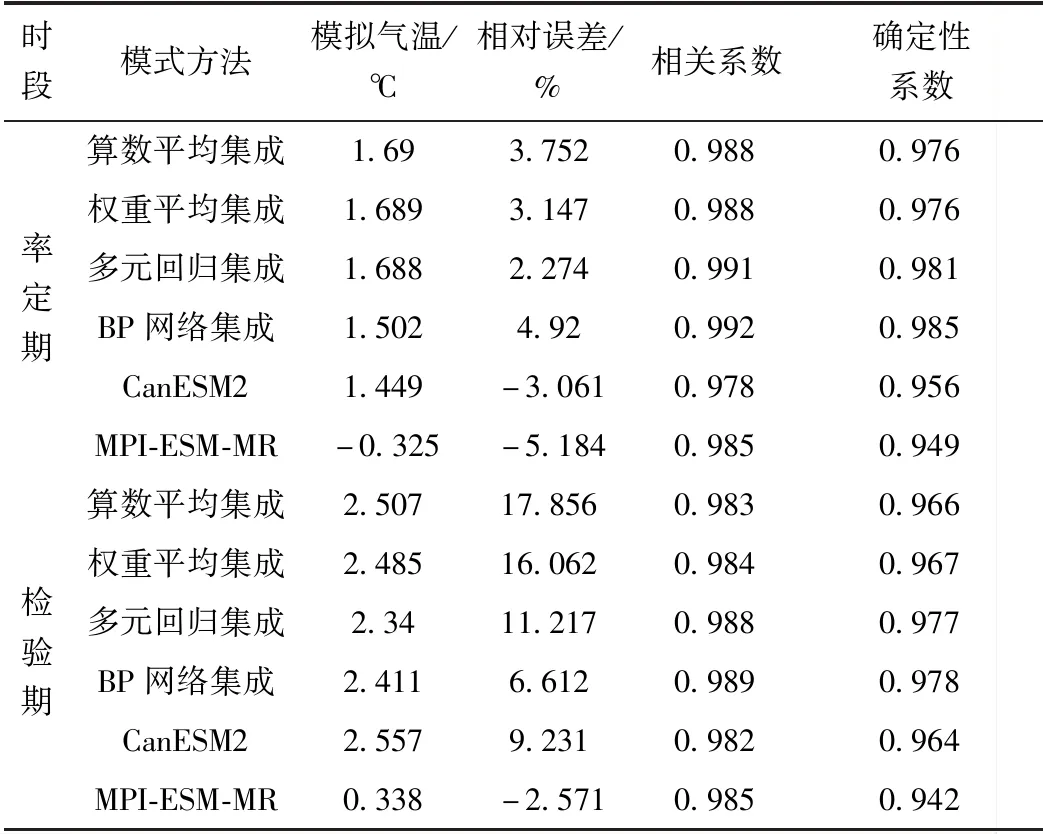
表5 氣溫模擬結果比較

由表5可知，模式模擬氣溫整體精度較高，各方法評估結果差別較小，平均相對誤差都較低，模擬氣溫和實測資料具有很高的相關性和吻合度。各方法模擬氣溫都較接近實際。

比較各方法模擬降水和氣溫的結果，集成方法整體優于單個模式。部分方法的平均相對誤差在檢驗期大于率定期的原因可能是模式數量選擇較少，BP網絡集成的試錯原理也存在一定的不確定性。最終認為多元回歸集成模擬降水和氣溫良好。

2.3 未來氣候要素預估

以所用模式在RCP4.5氣候情景輸出的結果為因子構建線性回歸方程預估未來降水和氣溫，方程通過了顯著性水平α=0.05的t檢驗和F檢驗。以松花江流域下游佳木斯站為例進行預估，佳木斯站氣候要素預估和實測的比較情況見圖2。佳木斯水文氣象要素預估和實測資料在年內平均變化的趨勢保持一致。

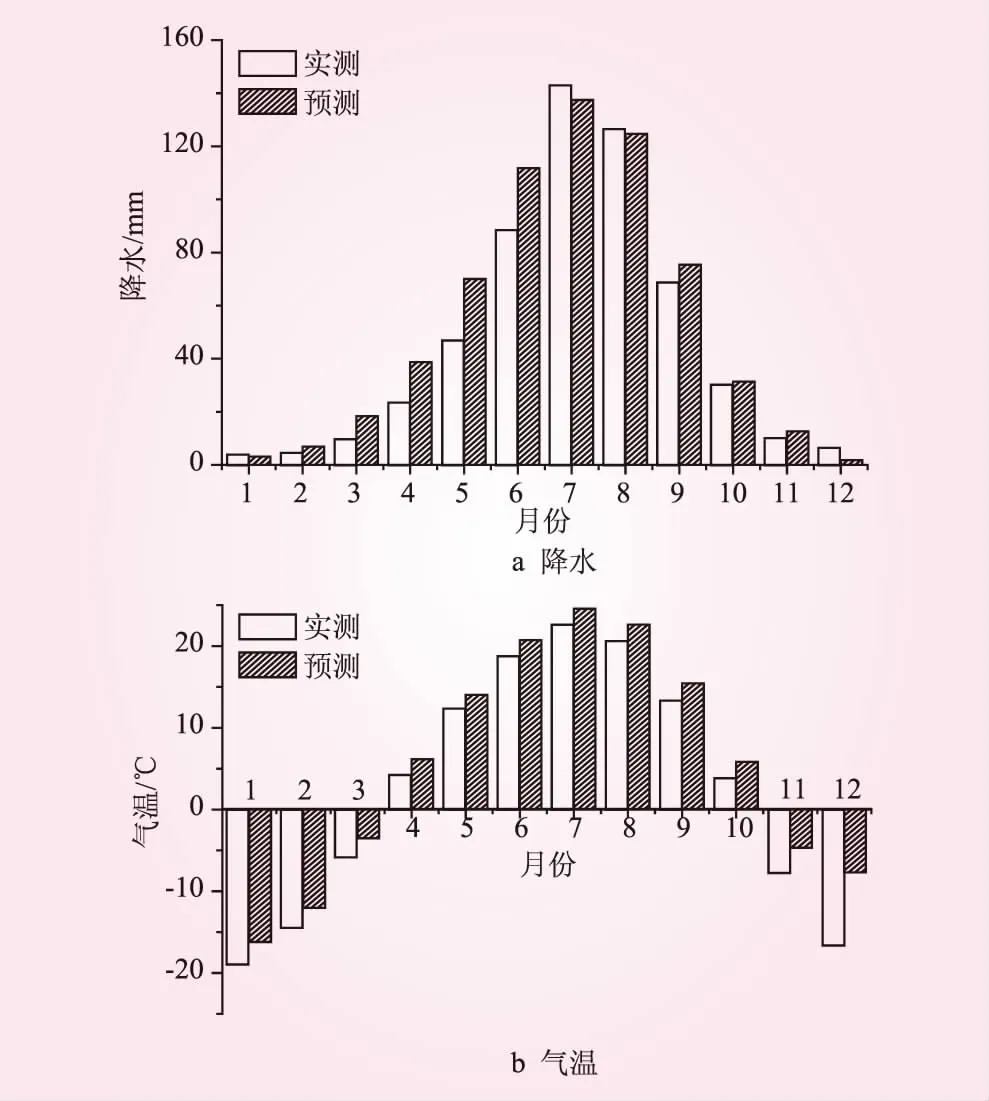
圖2 佳木斯站氣候要素年內平均變化

由圖2a可知，降水主要集中于汛期6月～9月，汛期降水實測總計達429 mm，預估為449 mm；實測降水在7月～8月較多而預估值偏小，其他月實測降水較少對應預估值基本偏大。

由圖2b知，平均氣溫最高值在7月，實測23 ℃，預估25 ℃；最低值在1月，實測-19 ℃，預估-16 ℃；多年平均氣溫實測2.71 ℃，預估5.43 ℃。預估氣溫普遍比實測偏高，平均增幅約為2 ℃。

2.4 未來徑流預估

2.4.1模型率定及檢驗

劃分1954年～2013年徑流歷史實測數據率定期為1954年～2003年，檢驗期為2004年～2013年。流域匯流存在滯后性，考慮上游降水對下游徑流的影響，按照區間降水氣溫和佳木斯站實測徑流的相關系數不低于0.5篩選因子，表7為主要影響因子及系數。多元回歸模擬和實測徑流的特征值見表8。

由表8可知，回歸模型整體模擬效果良好，率定期和檢驗期的平均相對誤差都低于10%，相關系數均超過0.8，和實測徑流均有較好的吻合度。

2.4.2未來徑流預估

利用優選方法預估降水和氣溫，結果輸入已構建的線性回歸模型來預估RCP4.5情景下佳木斯站2020年～2099年徑流的逐月變化。各模式修正系數：CanESM2降水0.91，氣溫1.331；MPI-ESM-MR降水0.718，氣溫2.883。

表7 徑流回歸因子及系數

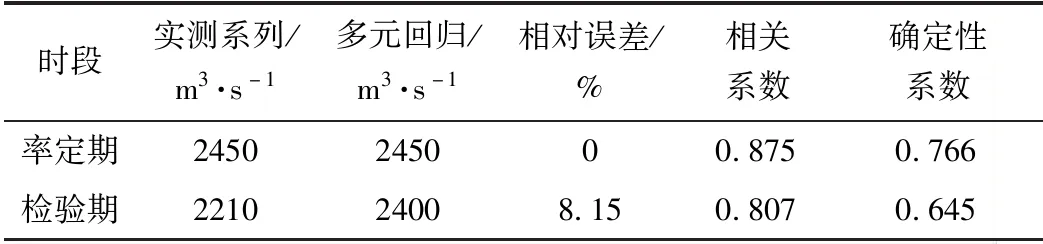
表8 多元回歸和實測徑流比較

多元回歸集成預估佳木斯站逐月徑流極大和極小值為7 220、352 m3/s，月平均值為2 720 m3/s；汛期總量19 600 m3/s，年總量達32 600 m3/s，豐枯水年界限值為33 700、31 500 m3/s。

3 結 論

本研究結果表明：①所用氣候模式中CanESM2、MPI-ESM-MR模擬良好。②集成方法模擬優于單個模式，多元回歸集成模擬較好。③佳木斯站實測和預估降水主要集中于汛期6月～9月，多年平均汛期總量實測429 mm，預估449 mm；預估降水在7月～8月比實測偏小，其他月相對偏大。④佳木斯站預估氣溫普遍比實測偏高，平均氣溫最高值都在7月，實測23 ℃，預估25 ℃；最低值都在1月，實測-19 ℃，預估-16 ℃；預估氣溫平均增幅約2 ℃。⑤多元回歸集成預估佳木斯站逐月徑流極大、極小值和月平均值分別為7 220、352 m3/s和2 720 m3/s；汛期總量19 600 m3/s，年總量達32 600 m3/s，豐枯水年界限值為33 700、31 500 m3/s。