水力式升船機鋼絲繩彈性模量對運行穩定性的影響*
全 強,薛 淑,胡亞安,李中華
(1.水利部牧區水利科學研究所,內蒙古 呼和浩特010020;2.南京水利科學研究院 通航建筑物建設技術交通行業重點實驗室,江蘇 南京 210029)
水力式升船機是一個涉及有壓管道水力學、閥門水力學、豎井水位與平衡重、鋼絲繩與平衡重、承船廂機械連接等方面的復雜系統[1]。通過輸水系統向各個豎井充泄水來改變豎井水位、驅動平衡重的升降從而通過鋼絲繩帶動承船廂升降運行[2]。因此,鋼絲繩是連接平衡重和船廂的柔性介質[3],鋼絲繩在升船機運行過程中的變形特性與船廂運行特性有密切關系。彈性模量是鋼絲繩的一個重要物性參數,因此研究水力式升船機鋼絲繩彈性模量對運行穩定性的影響有重要意義。
1 鋼絲繩彈性模量對船廂和平衡重附加位移特性的影響
對于水力升船機而言,在整個運行過程中,鋼絲繩繩端隨船廂(平衡重)經歷了啟動加速、逐漸減速、減速停靠3個過程[4-5],見圖1。本文對鋼絲繩的動力學特性進行仿真計算,通過繩端變形考察鋼絲繩變形對船廂(平衡重)附加位移特性的影響。
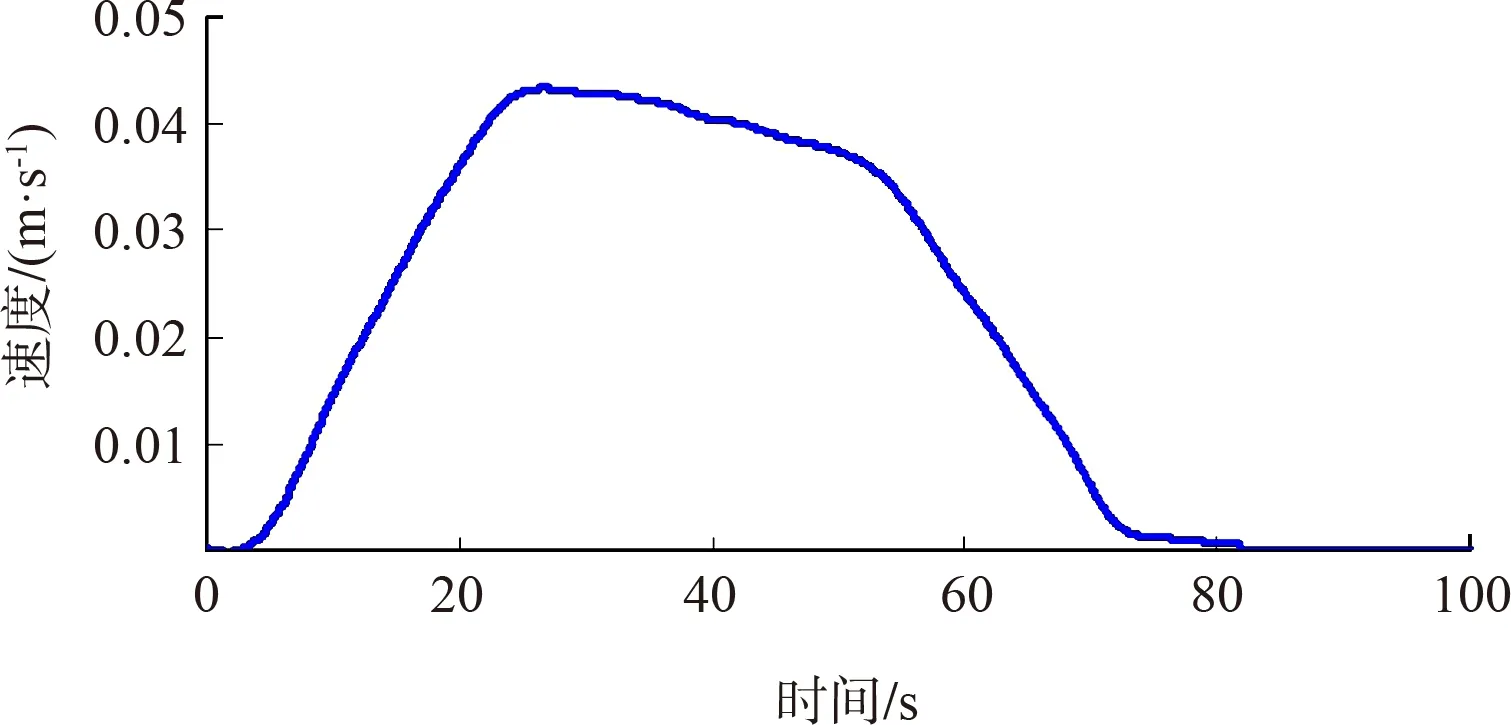
圖1 鋼絲繩繩端速度變化曲線
1.1 鋼絲繩運動微分方程
以鋼絲繩提升為例(圖2),考慮鋼絲繩作為一個柔性體所具有的特征,假設豎直向下為正方向,可推導鋼絲繩在加速、逐漸減速、減速停靠3個過程中的相對運動微分方程如下[6]:
(1)
式中:L(t)為繩端與卷筒之間的距離;m為提升質量;ρ為鋼絲繩單位長度的質量;E為繩彈性模量;F為橫截面積;S0為初始伸長量;S為繩端變形(相對位移);a為運行加速度。

圖2 鋼絲繩提升示意
1.2 船廂和平衡重附加位移特性
本文采用四階龍格——庫塔法[7]求解上述方程,對不同鋼絲繩彈性模量情況下的繩端總變形(即船廂和平衡重附加位移)特性進行對比分析。在圖1提升速度下,鋼絲繩彈性模量分別為10、20、50、100、200 GPa時,鋼絲繩的繩端變形過程見圖3。根據計算結果可得到繩端變形規律。
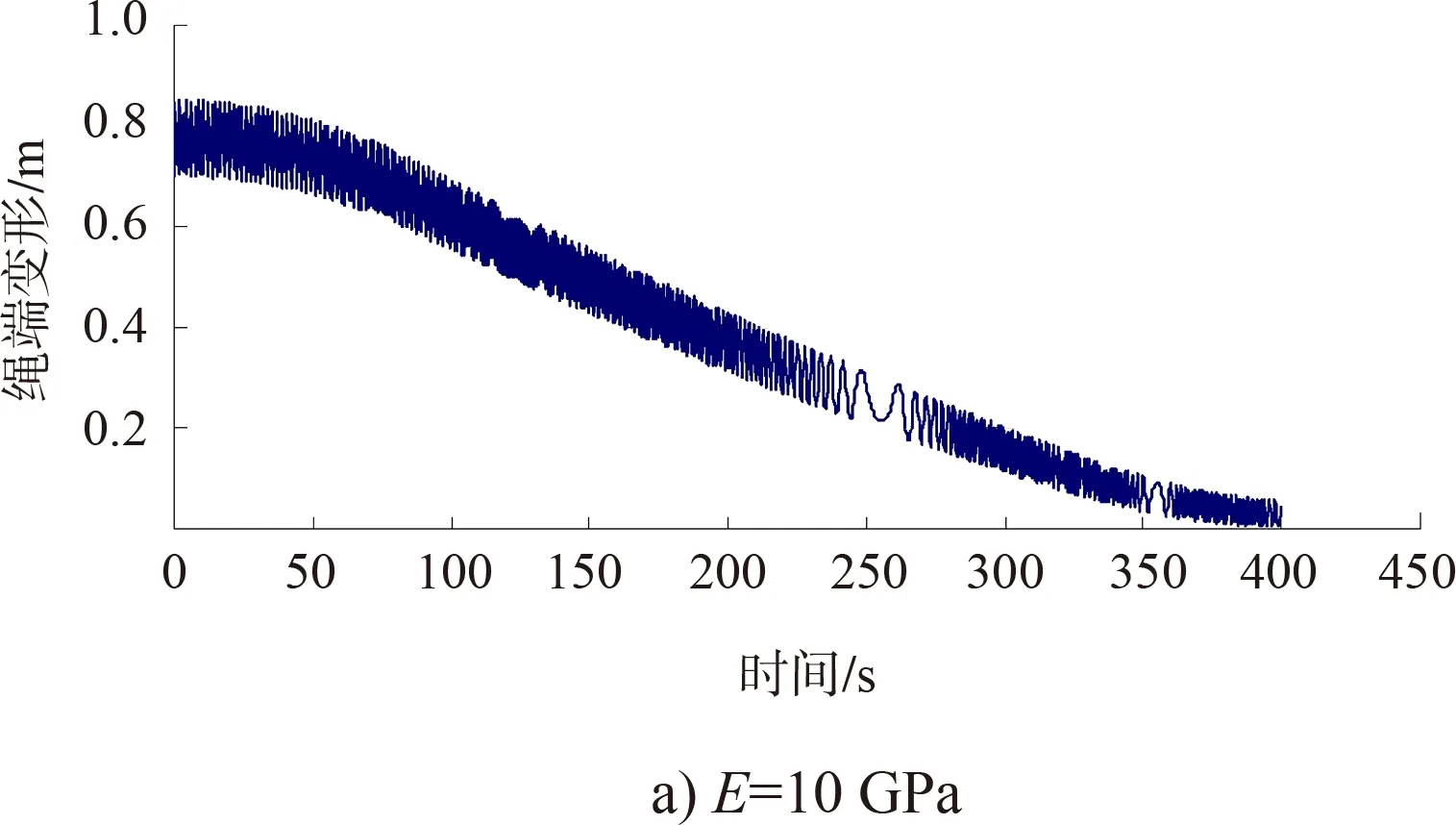

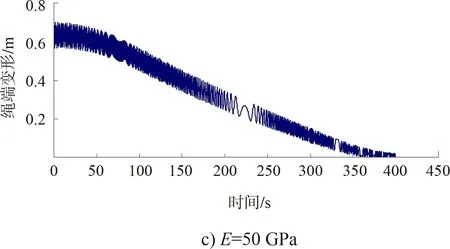
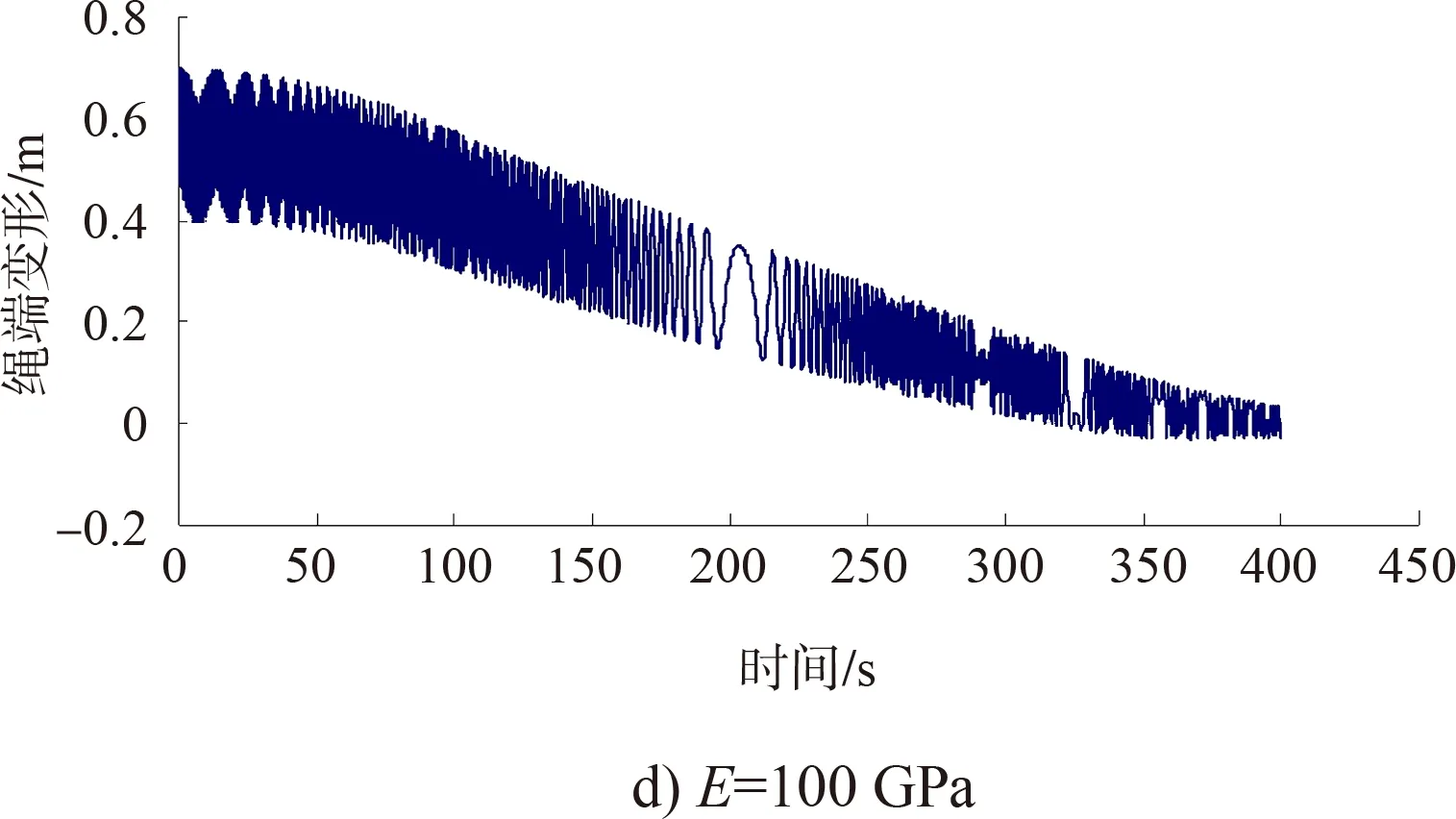
圖3 繩端變形過程
1)在鋼絲繩提升過程中,鋼絲繩端與卷筒之間的繩長逐漸縮短,因此繩端總變形量呈現減小的趨勢,船廂、平衡重提升至頂部,約400 s,鋼絲繩端總變形量最小。
2)鋼絲繩提升過程中,繩端變形量處在波動狀態,在加速終了和減速開始時發生明顯波動。
3)對比提升過程中繩端動態變形量的時域過程線可知,鋼絲繩彈性模量越大,鋼絲繩初始變形量越小。
4)當彈性模量為E< 20 GPa時,繩端變形量波動幅值隨鋼絲繩彈性模量的增加而減小;當彈性模量E> 20 GPa時,繩端變形量波動幅值隨鋼絲繩彈性模量的增加而增加,對船廂(平衡重)穩定上升越不利,見圖4。所以彈性模量E=20 GPa時,利于平衡重及承船廂的平穩運行。
圖4 不同彈性模量下繩端變形量
2 鋼絲繩彈性模量對船廂縱傾特性的影響
船廂縱傾量是考察升船機運行穩定性的重要指標。水力式升船機船廂縱傾量主要靠提高卷筒縱向同步軸剛度來控制,同時,鋼絲繩彈性模量對船廂縱傾量特性也產生附加影響。
建立“同步軸-鋼絲繩-載水船廂”概化三維耦合模型模擬船廂縱傾量變化[8],將船廂縱向鋼絲繩吊點布置簡化為首尾2個吊點,根據計算結果,船廂縱傾量典型變化特性如下:水力式升船機在啟動運行時,首先要克服同步軸扭轉間隙,在這個過程中,船廂縱傾量單調增加;水力式升船機在克服同步軸扭轉間隙后,同步軸剛度發揮作用抵抗船廂內水體產生的縱傾力矩,船廂縱傾量在平衡位置附近往復波動;船廂縱向傾斜量波動出現兩種優勢頻率,高頻振動反映了同步軸扭振的固有頻率,由于船廂水體的阻尼作用,衰減得很快,符合指數衰減的規律,低頻振動反映了船廂內水體的縱向一階自振頻率,由于數學模型中無法準確模擬系統阻尼及水體黏性的影響,因此衰減得很慢,實際工程中衰減更快。
保持同步軸剛度不變,計算不同鋼絲繩彈性模量條件下(E=即忽略鋼絲繩彈性變形)船廂的縱傾量變化特性,典型船廂縱傾量變化過程線對比見圖5。設同步軸扭振引起的船廂縱傾波動幅值為An,衰減常數為bns,同步軸扭振引起的船廂縱傾量波動頻率為ωn,廂內水體晃蕩引起的船廂縱傾量波動幅值為Az,船廂水體晃蕩引起的縱傾量波動頻率為ωz,鋼絲繩彈性模量對船廂縱傾量特性影響規律(圖6~7)如下:1)鋼絲繩彈性模量的改變對扭振引起的船廂縱傾量波動初始幅值基本沒有影響;2)鋼絲繩彈性模量影響同步軸扭振引起的船廂縱傾量波動頻率ωn,鋼絲繩彈性模量越小,頻率越高;3)鋼絲繩彈性模量越小,同步軸扭振引起的船廂縱傾量波動衰減速度越快,衰減常數bns與鋼絲繩彈性模量的倒數1E正相關;4)鋼絲繩彈性模量越大,即剛性越強,船廂的縱傾量越大,廂內水體晃蕩引起的船廂縱傾量波動幅值Az與鋼絲繩彈性模量的倒數1E呈負相關關系;5)鋼絲繩彈性模量對船廂水體晃蕩引起的縱傾量波動頻率ωz幾乎沒有影響。
圖5 鋼絲繩彈性模量對船廂縱傾量的影響

圖6 不同鋼絲繩彈性下同步軸扭振衰減過程
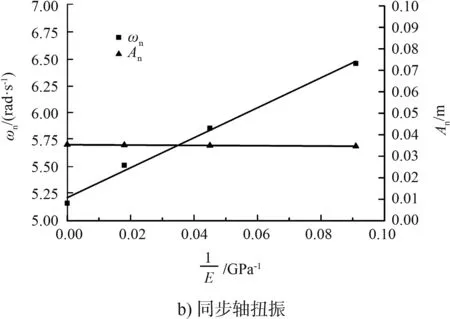
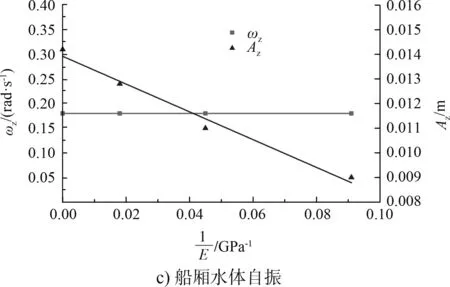
圖7 鋼絲繩彈性對船廂縱傾量特性的影響
3 結語
1)鋼絲繩在提升過程中,彈性模量E> 20 GPa時,彈性模量越大,繩端總變形量(即船廂與平衡重的附加位移)波動幅值越大;當彈性模量E< 20 GPa時,規律相反,故彈性模量E在20 GPa左右,有利于平衡重及承船廂的平穩運行。
2)鋼絲繩彈性模量越大,船廂水體縱向晃蕩引起的船廂縱傾波動幅值越大;同時,隨著鋼絲繩彈性模量的減小,同步軸扭振引起的船廂縱傾衰減速度加快。

