基于雨課堂的隨機信號分析理論實踐
汪 飛 徐文俊
(南京航空航天大學 江蘇·南京 211106)
0 引言
隨機信號分析是大學本科電子信息類必修的專業基礎課,以隨機過程作為學習與研究對象,概率與數理統計中隨機變量的基礎知識是其先導課程。當忽略隨機過程的觀測時間時,隨機過程的取值就轉變為概率論與數理統計課程中討論的隨機變量。比如古典概率中的擲色子,人們關注的是每次拋擲出現的點數,并不會去關注它出現的點數與時間的關系。隨機過程具有非常明確的時間概念,它是隨著時間而變化的,更貼近人們實際中遇到的生活與工程經歷。[1][2]簡而言之,隨機過程是結合了觀測時間的隨機變量。隨機信號分析的核心基礎是充分理解概率論中的隨機變量,以及隨機過程等基本概念。
“雨課堂”由清華大學在線教育辦公室組織研發,是一種快捷免費的為所有教學過程提供數據化、智能化信息支持的教學工具。它全面提升了課堂教學體驗,具有互動性強、操作簡單、反饋及時等優點。基于“雨課堂”的互聯網+教學模式能夠將課外預習與課堂教學相結合,讓課堂互動永不下線;能夠定制符合自己教學風格和教學節奏的教學設計,師生溝通及時反饋;能夠實現實時答題、彈幕互動,為課堂教學師生互動提供了完美解決方案;能夠科學地覆蓋課堂的每一個教學環節,為師生提供完整立體的數據支持,個性化報表、自動任務提醒,使教師及時了解學生的認知水平及不懂的難點。[3]
隨機信號分析教學過程中引入“雨課堂”,一方面可以利用“雨課堂”提供的各種便利新穎的教學模式,提高教學效率;另一方面可以通過有意設計課堂練習,利用“雨課堂”提供的數據報表實時將隨機信號分析理論與實踐相統一,達到學以致用的教學效果。
1 基于雨課堂教學數據的概率論理論實踐
概率論中的隨機變量是隨機信號分析教學的核心基礎之一。高斯型的概率密度函數是大學本科電子信息類專業最常見的一種隨機變量,其數學模型表示為:
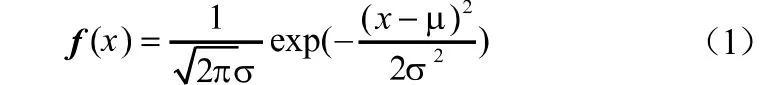
其中,代表樣本值,代表均值,代表標準差。隨機變量廣泛采用高斯型概率密度函數是它不僅能夠較好地描述絕大多數隨機變量的分布特征,而且具有非常好的可微可積特性,便于數學分析計算。
為了讓同學們能夠更直觀地理解高斯型“較好”描述隨機變量的程度,可以利用“雨課堂”以身高為變量設計單項選擇題。設計A 選項代表身高155~159 厘米,B 選項代表身高160~164 厘米,以此類推,任意兩個選項之間的身高數據完全不重合。同學們完成單項選擇之后的結果如圖1(a)所示,圖1(b)是用高斯型函數去擬合身高的概率統計結果。通過圖1(b)的對比,可以讓同學們清晰地了解到理論上的高斯型概率密度函數與現實統計數據之間的關系,認識到隨機信號分析理論中常用概率密度函數的出現并不是對現實世界的準確描述,而是在近似描述現實物理現象的同時方便利用數學工具。

圖1 身高的概率統計值及其高斯型擬合曲線
2 基于雨課堂教學數據的隨機過程理論實踐
準確理解隨機過程概念是隨機信號分析教學的另一個關鍵。簡單的隨機過程可以用數學模型表示為, ,其中 代表隨機變量, 指觀測時間起點用0 時刻表示,觀測時長為。
以某一班級作為隨機過程中的隨機變量樣本,該班對8 次課程的知識點掌握的人數統計結果如圖2 所示。可以看到絕大多數同學都掌握了8 個課程的知識點,表明該班級對隨機信號分析課程的學習理解能力具有平穩隨機過程的特性。
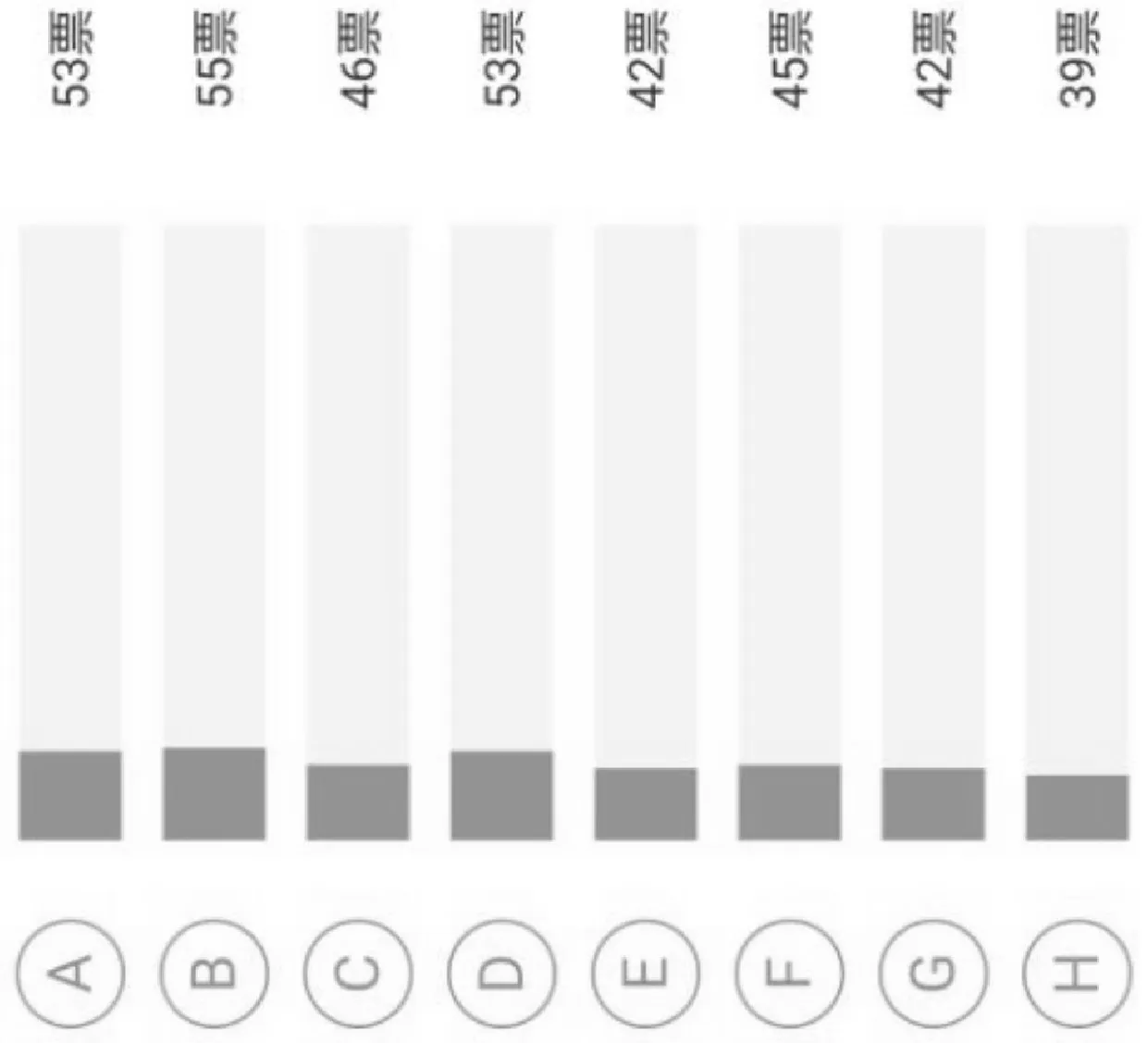
圖2 以某一班級作為隨機變量樣本的隨機過程樣本
3 總結
利用隨機過程分析隨機信號,是在人類尚未完全掌握信號產生機制條件下趨向可知方向發展的方法,其目標是掌握隨機信號的產生機制,實現可知論。隨機過程是經驗與知識的完美結合,充分利用“雨課堂”的特點,不僅能夠實時掌握同學們的知識點掌握程度,同時能夠讓同學們直接將理論應用于實踐。

