纖維混凝土抗凍性能及損傷劣化模型研究
趙小明,李?yuàn)W陽,喬宏霞,李江川,王新科
(1.甘肅第六建設(shè)集團(tuán)股份有限公司,蘭州 730046;2.蘭州理工大學(xué),西部土木工程防災(zāi)減災(zāi)教育部工程研究中心,蘭州 730050)
0 引 言
隨著經(jīng)濟(jì)的發(fā)展,國家建設(shè)規(guī)模持續(xù)擴(kuò)大,混凝土材料作為基本建筑材料,因原材料普通常見,且具有優(yōu)良的可塑性、耐久性和強(qiáng)度高等特點(diǎn)而被廣泛應(yīng)用。對(duì)一些特殊地區(qū)、特殊建筑來說,普通混凝土已經(jīng)無法滿足使用要求,為尋求更具特色且適用性強(qiáng)的混凝土材料,纖維混凝土因此而產(chǎn)生。纖維主要是通過橋接作用來限制微觀裂縫的發(fā)展[1],從而改善混凝土的強(qiáng)度及耐久性。在我國北方嚴(yán)寒地區(qū),混凝土建筑因長期處于低溫環(huán)境,凍融循環(huán)經(jīng)常發(fā)生,由于溫度影響,導(dǎo)致其出現(xiàn)過多裂縫,嚴(yán)重影響了建筑的安全和使用壽命[2]。因此,在混凝土凍融循環(huán)后,考慮如何預(yù)防和阻斷裂縫的出現(xiàn)顯得十分重要。
趙燕茹等[3]對(duì)凍融循環(huán)作用后玄武巖纖維混凝土的斷裂性能進(jìn)行了研究,發(fā)現(xiàn)隨凍融循環(huán)次數(shù)的增加,玄武巖纖維混凝土的斷裂性能大幅度下降,玄武巖纖維不能較好地抑制凍融循環(huán)給混凝土帶來的損傷。程紅強(qiáng)等[4]進(jìn)行了聚丙烯纖維混凝土凍融損傷試驗(yàn),在凍融循環(huán)作用下,聚丙烯纖維混凝土損傷不斷累加,質(zhì)量損失率和劈拉強(qiáng)度不斷降低,隨著纖維摻量的增加,混凝土的劈拉強(qiáng)度不斷提高。嚴(yán)武建等[5]探討了凍融循環(huán)作用下聚丙烯纖維混凝土的力學(xué)性能,發(fā)現(xiàn)摻加引氣劑的聚丙烯纖維混凝土在經(jīng)過凍融后,引氣劑對(duì)聚丙烯纖維混凝土的抗壓強(qiáng)度具有不利影響,摻入引氣劑的C30聚丙烯纖維混凝土的質(zhì)量損失率更低。陳升平等[6]研究了凍融環(huán)境下纖維混凝土的損傷模型,根據(jù)試驗(yàn)所得數(shù)據(jù)進(jìn)行擬合分析發(fā)現(xiàn),隨著凍融次數(shù)的增加,混凝土的損傷度逐漸增大,且動(dòng)彈性模量所定義的損傷變量更能直觀地反映混凝土的凍融損傷程度。其他學(xué)者關(guān)于纖維混凝土抗凍性的研究也有不同看法[7-11]。混凝土的破壞過程主要表現(xiàn)為裂縫的產(chǎn)生和擴(kuò)大[12],因此,加入纖維能有效抑制裂縫發(fā)展,對(duì)混凝土的性能具有顯著提升作用。
目前對(duì)單摻纖維混凝土抗凍性研究成果頗豐,而對(duì)混雜纖維混凝土抗凍性研究較少。因此本文通過鋼纖維(SFs)和PVA纖維混合摻入混凝土,采用正交配比制成混凝土試件,采集相應(yīng)凍融次數(shù)的質(zhì)量損失率、相對(duì)動(dòng)彈性模量和抗壓、劈裂抗拉強(qiáng)度等數(shù)據(jù),分析不同比例的纖維對(duì)混凝土抗凍性的影響,然后通過二次函數(shù)擬合得出凍融次數(shù)與相對(duì)動(dòng)彈性模量、強(qiáng)度的衰減模型。同時(shí)根據(jù)損傷理論,建立纖維混凝土凍融損傷模型,可為凍融循環(huán)作用下混雜纖維混凝土的試驗(yàn)研究提供有效參考。
1 實(shí) 驗(yàn)
1.1 原材料和配合比
水泥選用P·O 42.5級(jí)普通硅酸鹽水泥;粗骨料選用直徑為5~20 mm,表觀密度為2 700 kg/m3的碎石;細(xì)骨料選用河砂,細(xì)度模數(shù)3.18;減水劑選用羥系減水劑,減水率為20%;水選用蘭州普通自來水;纖維選用鋼纖維(SFs)和PVA纖維,來源于河北某纖維廠,其物理性能見表1;依據(jù)JGJ 55—2011《混凝土配合比設(shè)計(jì)規(guī)程》[13]制備標(biāo)準(zhǔn)混凝土,其配合比見表2;粉煤灰選用Ⅱ級(jí)粉煤灰,由甘肅蘭州某廠提供,其主要指標(biāo)見表3。

表1 纖維主要物理性能參數(shù)Table 1 Main physical property parameters of fiber

表2 混凝土配合比Table 2 Mix proportion of concrete

表3 粉煤灰主要指標(biāo)Table 3 Main indicators of fly ash
1.2 實(shí)驗(yàn)過程及方法
混雜纖維混凝土的凍融循環(huán)試驗(yàn)以纖維的摻入量為基本變化數(shù),按預(yù)先制定的配合比來制備混凝土試件。首先,按計(jì)算配合比稱取所需混凝土材料用量,將碎石、砂、水泥和粉煤灰倒入攪拌機(jī),先干拌30 s后加入3/4的水,開始濕拌,再按不同配比加入纖維攪拌均勻,然后把剩余的水、減水劑倒入攪拌機(jī),攪拌完成后倒入準(zhǔn)備好的規(guī)格為100 mm×100 mm×100 mm的立方體試模和100 mm×100 mm×400 mm的棱柱體試模內(nèi),把模具中的混凝土振動(dòng)均勻密實(shí),最后把模具表面抹平。試件標(biāo)準(zhǔn)養(yǎng)護(hù)24 h后進(jìn)行拆模,拆模后放在標(biāo)準(zhǔn)養(yǎng)護(hù)室養(yǎng)護(hù)28 d。取出試件,在凍融循環(huán)試驗(yàn)開始之前,將試件放在(20±3) ℃的水中,試件的上表面應(yīng)距水面20 mm左右,浸泡4 d做凍融試驗(yàn),在試驗(yàn)過程中需要保證纖維混凝土試件一直處于全浸水狀態(tài)。凍融試驗(yàn)過程中,最低中心溫度和最高中心溫度應(yīng)分別控制在(-17±2) ℃和(8±2) ℃。每凍融循環(huán)25次為一階段,測量所需的數(shù)據(jù),一次凍融循環(huán)大約2~4 h,凍融次數(shù)達(dá)到100次時(shí),試驗(yàn)終止。
對(duì)于混凝土在凍融循環(huán)試驗(yàn)中,凍融損傷的兩個(gè)重要參數(shù)分別為質(zhì)量損失率和相對(duì)動(dòng)彈性模量,定義質(zhì)量損失率為Wn和相對(duì)動(dòng)彈性模量為Pn,如式(1)、(2)所示。
(1)
(2)
式中:G0為凍融前試件的質(zhì)量;Gn為凍融n次后試件的質(zhì)量;f0為凍融前試件橫向共振頻率;fn為凍融n次后試件橫向共振頻率。
2 結(jié)果與討論
2.1 凍融循環(huán)下混凝土質(zhì)量和相對(duì)動(dòng)彈性模量分析
圖1為不同摻量下纖維混凝土的凍融次數(shù)和質(zhì)量損失率之間的關(guān)系曲線圖。從圖中可以看出,凍融次數(shù)達(dá)到25次時(shí),試件的質(zhì)量損失率曲線逐步降低,表明試件在經(jīng)過凍融循環(huán)后,質(zhì)量有了一定的負(fù)增長,從質(zhì)量損失率程度來看,JZ>SPC-4>SPC-3>SPC-2>SPC-1,其主要原因是試件內(nèi)部出現(xiàn)微裂縫,這些微裂縫隨凍融次數(shù)的增加開始逐漸擴(kuò)大且吸收水分,試件外部趨于完整,混凝土脫落的質(zhì)量小于吸收水分的質(zhì)量,從曲線變化可以看出,試件在凍融循環(huán)初期,質(zhì)量都會(huì)因內(nèi)部出現(xiàn)微裂縫吸水而增加;凍融25次至100次,試件的質(zhì)量損失率曲線表現(xiàn)為增長趨勢,即質(zhì)量開始正增長,原因是隨著凍融次數(shù)的增加,混凝土外部出現(xiàn)損傷,表面裂縫逐步擴(kuò)大,開始出現(xiàn)明顯的水泥砂漿脫落,混凝土脫落的質(zhì)量遠(yuǎn)遠(yuǎn)大于微裂縫吸收水分的質(zhì)量。從圖中曲線可以看出,JZ不摻加任何纖維,質(zhì)量損失率最多,為1.86%,SPC-3質(zhì)量損失率最少,為1.16%,原因是SFs-PVA纖維在混凝土中亂向分布,對(duì)開裂具有抑制效果,約束了外部損傷,摻入纖維可以有效降低質(zhì)量損失率。SPC-1和SPC-4對(duì)比SPC-2和SPC-3的曲線,顯然SPC-2和SPC-3的質(zhì)量損失率更少。試件在經(jīng)過100次凍融循環(huán)后,其質(zhì)量損失率為:JZ>SPC-4>SPC-1>SPC-2>SPC-3。

圖1 纖維混凝土的質(zhì)量損失率與凍融次數(shù)的關(guān)系曲線 Fig.1 Relationship curves between mass loss rate of fiber reinforced concrete and number of freeze-thaw cycles
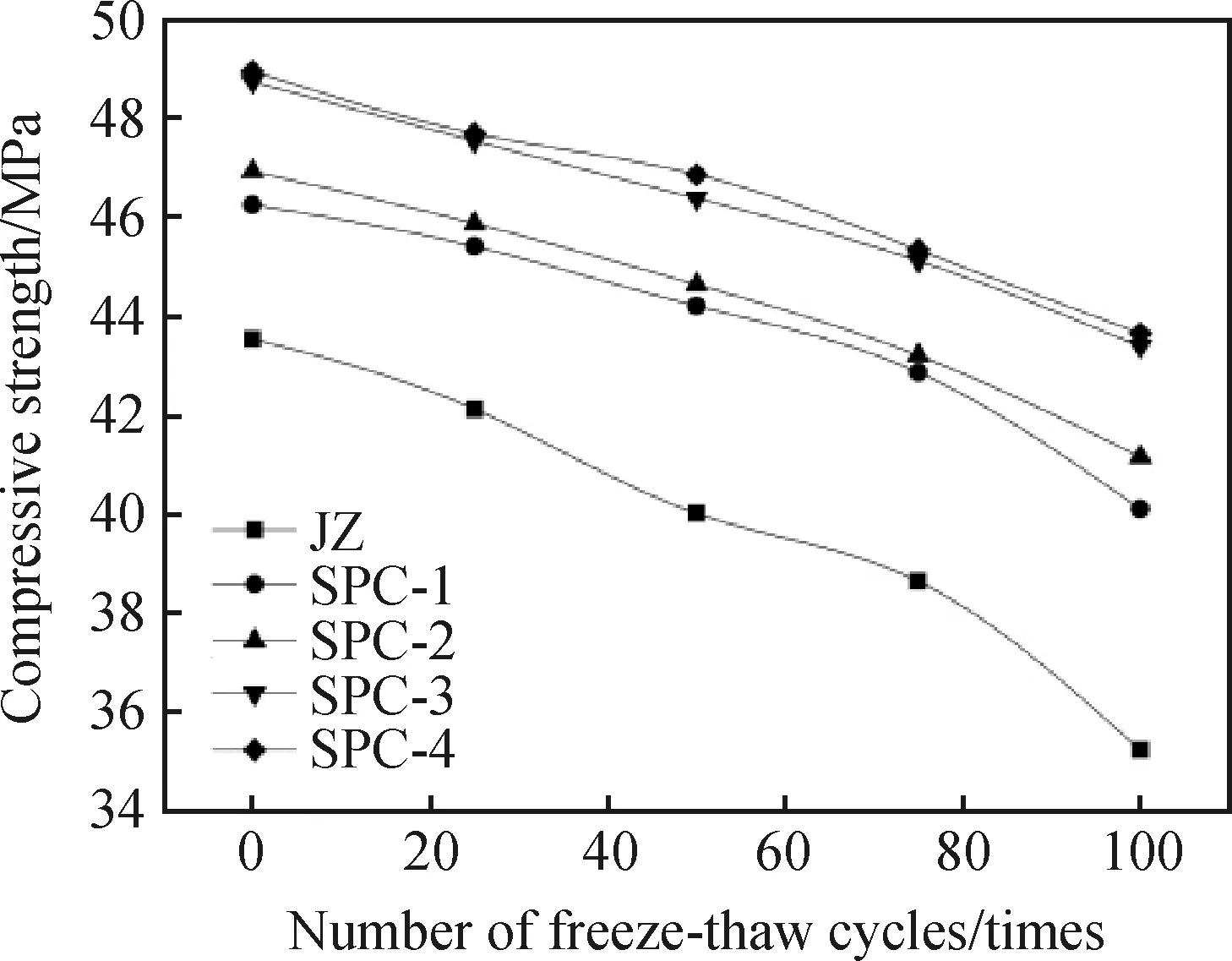
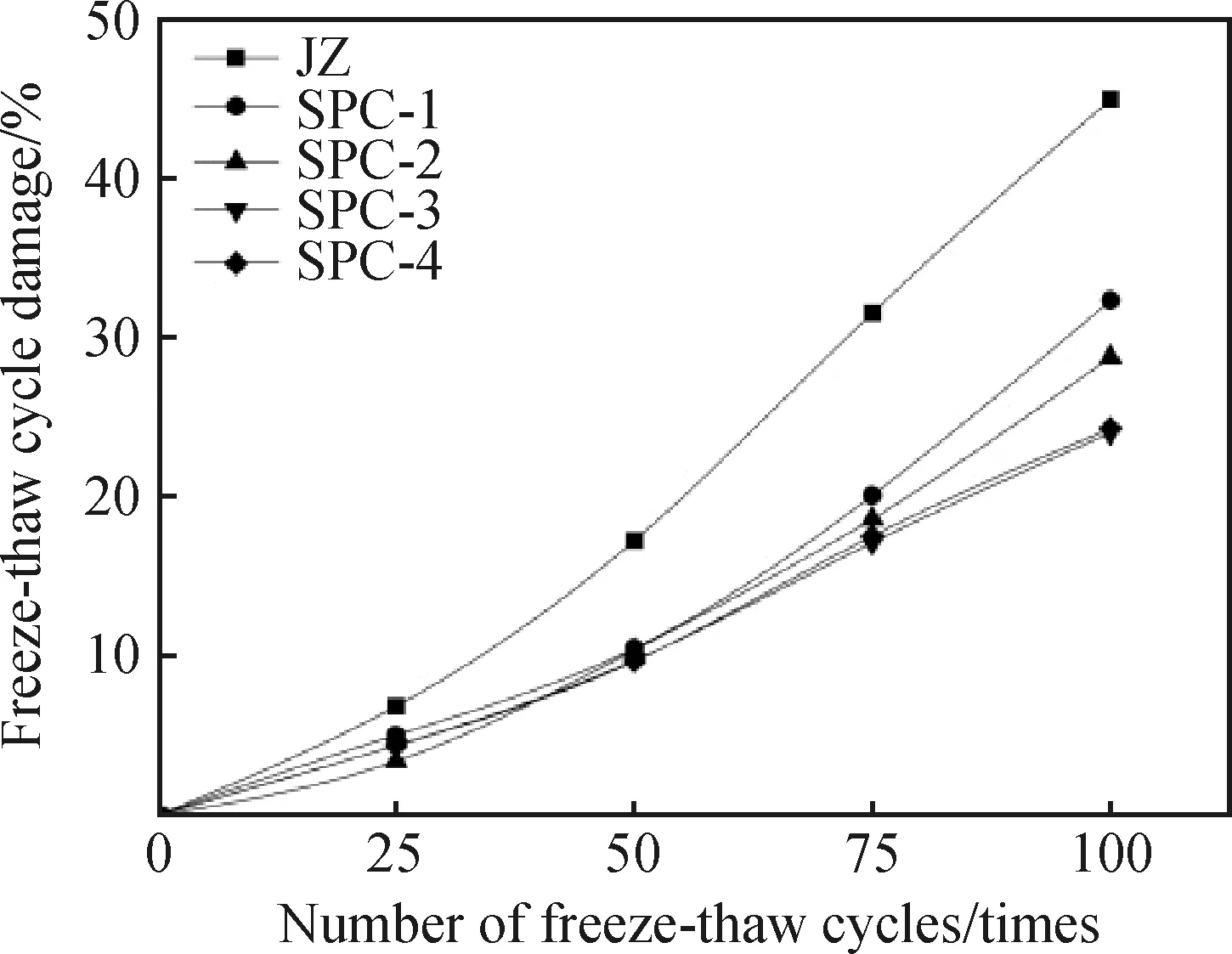
圖2為不同摻量下纖維混凝土的凍融次數(shù)和相對(duì)動(dòng)彈性模量之間的關(guān)系曲線圖。凍融次數(shù)從0次到100次期間,相對(duì)動(dòng)彈性模量曲線不斷下降,下降幅度明顯不同。凍融次數(shù)達(dá)到100次時(shí),JZ和SPC-4組試件下降幅度最大,都發(fā)生了嚴(yán)重的損傷,相比來看,SPC-1、SPC-2和SPC-3的相對(duì)動(dòng)彈性模量下降幅度相對(duì)平緩,損傷均小于前兩組。對(duì)比JZ和SPC-1、SPC-2、SPC-3的曲線來看,JZ的相對(duì)動(dòng)彈性模量損失速率最快,抗凍性較差,其他三組相對(duì)動(dòng)彈性模量曲線平緩下降,損失速率較慢,說明纖維能夠改善混凝土內(nèi)部結(jié)構(gòu),防止微裂縫增大,降低混凝土凍融損傷程度,對(duì)于混凝土的抗凍性起到有利效果[14];對(duì)比SPC-1和SPC-2,粉煤灰可使混凝土內(nèi)部更加密實(shí),摻量的增加對(duì)減小相對(duì)動(dòng)彈性模量損失具有積極影響;SPC-4相較于其他三組,相對(duì)動(dòng)彈性模量下降的幅度最大且損傷最嚴(yán)重,表明SFs和PVA纖維阻斷混凝土內(nèi)部出現(xiàn)微裂縫的性能減弱,導(dǎo)致試件的強(qiáng)度和密實(shí)性下降。試件在經(jīng)過100次凍融循環(huán)后,其相對(duì)動(dòng)彈性模量為:SPC-4 圖2 纖維混凝土的相對(duì)動(dòng)彈性模量與凍融次數(shù)的關(guān)系曲線 Fig.2 Relationship curves relative dynamic elastic modulus of fiber reinforced concrete and number of freeze-thaw cycles 圖3和圖4分別為不同摻量下纖維混凝土的凍融次數(shù)和抗壓、抗拉強(qiáng)度之間的關(guān)系曲線圖。從圖中可以看出,隨著凍融次數(shù)的增加,試件抗壓強(qiáng)度和抗拉強(qiáng)度曲線均在同步下降,在相同凍融循環(huán)次數(shù)下,其強(qiáng)度大小從高到低依次為:SPC-4>SPC-3>SPC-2>SPC-1>JZ。從開始凍融到試驗(yàn)結(jié)束,JZ的抗壓強(qiáng)度和抗拉強(qiáng)度損失率分別是19%和45%,含有纖維的試件SPC-1、SPC-2、SPC-3和SPC-4的強(qiáng)度損失率明顯低于JZ,說明在凍融循環(huán)試驗(yàn)中,纖維能夠有效地提高混凝土的抗凍性和強(qiáng)度。基于圖中曲線的變化規(guī)律,SPC-1和SPC-2對(duì)比SPC-3和SPC-4,在經(jīng)過100次凍融循環(huán)試驗(yàn)過程中,SPC-3和SPC-4的抗壓、抗拉強(qiáng)度始終高于SPC-1和SPC-2,即在一定條件下,SFs摻入量越多,試件強(qiáng)度的提升越大,這是因?yàn)镾Fs能約束混凝土的橫向膨脹力[15],同時(shí)抑制裂縫的出現(xiàn),進(jìn)而提高混凝土強(qiáng)度。通過SPC-1和SPC-2強(qiáng)度變化曲線趨勢可以看出,在凍融循環(huán)初期,由于混凝土試件損傷并不嚴(yán)重,抗壓和抗拉強(qiáng)度差值不大,隨著凍融循環(huán)繼續(xù)進(jìn)行,混凝土試件的損傷逐漸增加,導(dǎo)致抗拉和抗壓強(qiáng)度的差值逐步擴(kuò)大。凍融循環(huán)50次到100次期間,試件抗壓、抗拉強(qiáng)度曲線下降速率逐步加快,下降斜率大于凍融循環(huán)初期,說明隨著凍融次數(shù)的增加,SFs和PVA纖維與混凝土之間的橋接作用和粘結(jié)性遭到破壞,試件內(nèi)部損傷進(jìn)一步加劇,通過纖維來提高混凝土抗凍性能的作用逐步削弱。但總而言之,在混凝土中摻入纖維,能夠減緩強(qiáng)度損失速率,減小混凝土橫向膨脹速度,改善內(nèi)部結(jié)構(gòu),提高混凝土的抗凍性。 圖3 纖維混凝土的抗壓強(qiáng)度與凍融次數(shù)的關(guān)系曲線 Fig.3 Relationship curves between compressive strength of fiber reinforced concrete and number of freeze-thaw cycles 圖4 纖維混凝土的抗拉強(qiáng)度與凍融次數(shù)的關(guān)系曲線 Fig.4 Relationship curves between tensile strength of fiber reinforced concrete and number of freeze-thaw cycles 混凝土試件在制備過程中,由于粗骨料、細(xì)骨料等材料形狀不規(guī)則,大小不統(tǒng)一,在攪拌過程中不能完全無縫銜接,導(dǎo)致其內(nèi)部出現(xiàn)孔隙,這些孔隙微小且數(shù)量很多,是影響混凝土抗凍性的一個(gè)重要因素。凍融損傷是混凝土在凍融循環(huán)過程中,由于外界環(huán)境的變化,內(nèi)部孔隙產(chǎn)生了一定的橫向膨脹力,導(dǎo)致這些孔隙逐漸發(fā)展為微裂縫而出現(xiàn)耐久性問題[16],凍融次數(shù)不斷增加,凍融損傷就不斷擴(kuò)大,最終導(dǎo)致混凝土表面開裂,出現(xiàn)骨料或者砂漿的脫落。 相對(duì)動(dòng)彈性模量能夠有效反映出混凝土的凍融損傷程度[17-18],可較好地對(duì)損傷度進(jìn)行評(píng)價(jià)。基于相對(duì)動(dòng)彈性模量的數(shù)據(jù)變化,根據(jù)混凝土損傷力學(xué),混凝土的凍融循環(huán)損傷程度D可用式(3)表示。 (3) 式中:En為凍融n次后試件的動(dòng)彈性模量;E0為凍融前試件的初始動(dòng)彈性模量。 將混凝土試件的相對(duì)動(dòng)彈性模量數(shù)據(jù)代入式(3)可以得出隨凍融循環(huán)次數(shù)增加,凍融循環(huán)損傷程度的變化趨勢,如圖5所示。 圖5 損傷程度D和凍融次數(shù)的關(guān)系曲線Fig.5 Relationship curves between damage degree D and number of freeze-thaw cycles 從圖5中可以看出,所有試件的凍融循環(huán)損傷程度曲線均表現(xiàn)為上升趨勢,凍融次數(shù)越多,損傷程度越大。和圖2相比可以發(fā)現(xiàn),相對(duì)動(dòng)彈性模量越大,試件的損傷就越小。凍融循環(huán)100次后,SPC-4損傷程度最大,凍融損傷速率上升最快;SPC-3損傷程度最小,凍融損傷速率上升最慢。 為考慮凍融循環(huán)與混凝土力學(xué)性能衰減規(guī)律的變化,分析抗壓、抗拉強(qiáng)度與凍融循環(huán)損傷程度之間的關(guān)系,定義DC為抗壓或抗拉下凍融循環(huán)損傷程度,可用式(4)表示。 (4) 式中:fcn為凍融n次后試件的抗壓或抗拉強(qiáng)度;fc0為凍融前試件的抗壓或抗拉強(qiáng)度。 將混凝土試件的抗壓、抗拉強(qiáng)度數(shù)據(jù)代入式(4)可以得出隨著凍融循環(huán)次數(shù)的增加,凍融循環(huán)損傷程度的變化趨勢,如圖6、圖7所示。 圖6 抗壓強(qiáng)度下凍融循環(huán)損傷程度和凍融次數(shù)的關(guān)系曲線Fig.6 Relationship curves between the degree of freeze-thaw cycle damage and the number of freeze-thaw cycles under compressive strength 圖7 抗拉強(qiáng)度下凍融循環(huán)損傷程度和凍融次數(shù)的關(guān)系曲線Fig.7 Relationship curves between the degree of freeze-thaw cycle damage and the number of freeze-thaw cycles under tensile strength 從圖6和圖7中可以看出,抗壓、抗拉強(qiáng)度下凍融循環(huán)損傷程度最大的是JZ,其次是SPC-1。抗壓、抗拉強(qiáng)度的損失速度與凍融損傷是相關(guān)聯(lián)的,凍融損傷越大,孔隙和微裂縫越多,試件內(nèi)部破壞越嚴(yán)重,抗壓、抗拉強(qiáng)度下降越快。 為了能夠更加準(zhǔn)確地反映混雜纖維混凝土的凍融損傷程度,因此構(gòu)建混雜纖維混凝土的二次函數(shù)衰減模型,如式(5)所示。 Y=aN2+bN+c (5) 式中:a、b、c為材料系數(shù);N為凍融次數(shù)。 將動(dòng)彈性模量、抗壓強(qiáng)度和抗拉強(qiáng)度的凍融損傷程度分別代入式(5)進(jìn)行擬合,處理擬合結(jié)果,得到衰減模型如表4~表6所示。 表4 凍融循環(huán)損傷程度二次函數(shù)衰減系數(shù)Table 4 Attenuation coefficient of quadratic function of damage degree of freeze-thaw cycle 表5 抗壓強(qiáng)度下凍融循環(huán)損傷程度二次函數(shù)衰減系數(shù)Table 5 Attenuation coefficient of quadratic function of damage degree of freeze-thaw cycle under compressive strength 表6 抗拉強(qiáng)度下凍融循環(huán)損傷程度二次函數(shù)衰減系數(shù)Table 6 Attenuation coefficient of quadratic function of damage degree of freeze-thaw cycle under tensile strength 從表4~表6中可以看出,擬合系數(shù)R2最低為0.969 52,大部分?jǐn)M合系數(shù)均在0.99以上,表明建立的二次函數(shù)衰減模型具有很高的精準(zhǔn)度,與試驗(yàn)結(jié)果有較好的擬合程度,對(duì)混雜纖維混凝土的凍融循環(huán)損傷程度能夠起到很好的預(yù)測效果。 (1)試件的質(zhì)量損失率在凍融初期呈現(xiàn)為負(fù)增長趨勢;隨凍融循環(huán)次數(shù)的增加,質(zhì)量損失率曲線逐步上升,相對(duì)動(dòng)彈性模量曲線逐步下降;通過對(duì)比分析,SFs和PVA纖維的摻入能夠有效降低質(zhì)量損失率,提高相對(duì)動(dòng)彈性模量,其中以SPC-3的摻量得到的性能最優(yōu);摻入適量粉煤灰可有效提高混凝土密實(shí)性,抑制試件損傷開裂。 (2)隨著凍融次數(shù)的增加,混凝土試件的強(qiáng)度不斷下降,摻入混雜纖維的試件強(qiáng)度要高于標(biāo)準(zhǔn)試件,其中以SPC-4的摻入方式得到的抗壓、抗拉強(qiáng)度最大,抗凍性最優(yōu)。 (3)基于試驗(yàn)得到的相對(duì)動(dòng)彈性模量和抗壓、抗拉強(qiáng)度的數(shù)據(jù)進(jìn)行凍融循環(huán)損傷程度分析,結(jié)果表明混凝土中摻入纖維及粉煤灰可以降低損傷程度;根據(jù)數(shù)據(jù)擬合的二次函數(shù)衰減模型,其擬合系數(shù)大部分均在0.99以上,可較好地反映纖維混凝土凍融損傷變化規(guī)律。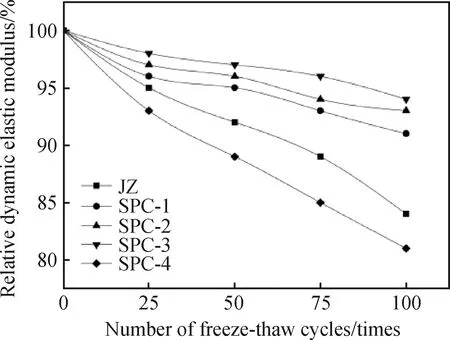
2.2 凍融循環(huán)下混凝土抗壓和抗拉強(qiáng)度分析

3 混雜纖維混凝土凍融損傷模型分析





4 結(jié) 論

