污染環境中微生物治理種群動力學優化算法*

黃光球，陸秋琴

西安建筑科技大學 管理學院，西安 710055

1 引言

群智能算法是利用一些特殊自然現象開發出來的算法，對復雜優化問題具有很好的適應性。此類算法近幾年得到了快速發展。早期的群智能算法所利用的自然現象都很簡單，因而這些算法的結構較簡單[1-5]等。然而，隨著面臨的優化問題越來越復雜且維數不斷增加，傳統的基于簡單自然現象的簡單結構群智能算法向基于復雜自然現象的復雜結構群智能算法演變是必然趨勢。

種群動力學是采用數學方法描述種群個體相互作用關系[6]。由于種群中的個體可以解釋為優化問題中的試探解，個體間的相互作用可以映射成試探解的改進，種群的進化活動可以映射成算法的邏輯結構。因此，種群動力學與群智能算法具有天然的聯系。

文獻[7]采用保護區種群遷移動力學模型構造出了PZPMDO（protected zone-based population migration dynamics optimization）算法，該算法利用保護區與非保護區之間的種群遷移行為構建出進化算子；文獻[8]采用捕食-被食動力學模型構造出了OA-PPD（optimization algorithm based on predator-prey dynamics with competition among the same species）算法，該算法的演化算子是基于兩種群間的捕食和被食行為而構造出來的；文獻[9]利用微生物培養動力學模型構造出了MDO（microbial dynamics optimization）算法，該算法的演化算子是基于微生物種群在營養物質和有害物質作用下的生長特征變化規律而構建出來的；文獻[10]利用Lotka-Volterra 生態平衡動力學模型構造出了EBDO（ecological balance dynamics-based optimization）算法，該算法利用生態系統中消費者種群、自養者種群和分解者種群相互間的營養供給關系構造出了演化算子。

水體富營養化是指在人類活動的影響下，氮磷等物質大量進入湖泊、河流、池塘等緩流水體，引起藻類及其他浮游生物迅速繁殖，水體溶解氧量下降、水質惡化、魚類及其他生物大量死亡的現象[11]。20 世紀70 年代興起的生物修復技術相比傳統技術具有費用低且不會發生二次污染的優點[11]，正在逐步被推廣。研究表明，微生物在水體富營養化的治理中可以發揮重要作用[12-15]。

一個池塘中水體的富營養化及其生物治理過程是一個較復雜的自然現象，該復雜自然現象能夠被數學模型很好描述。本文基于具微生物治理和基因突變，且種群內部個體之間具有競爭關系的種群動力學模型，提出了一種新的種群動力學優化算法，簡稱PDO-MCCE（population dynamics optimization algorithm under microbial control in contaminated environment）算法。在該算法中，采用了與現有種群動力學優化算法不同的設計思路，構造出的算子可以充分反映正常種群、突變種群、環境有害物質和微生物種群之間的相互作用關系[9]，該算法適用于求解高維優化問題[9-10，16-19]。

2 算法基本原理

2.1 算法場景設計

假設在一個池塘的水體中生活有一種生物種群，該種群由若干個生物個體組成，這些個體的編號形成的集合為A1={1，2，…，Q1}，該種群稱為正常種群A。池塘周圍建有若干家化工廠，每隔一段時間，這些化工廠向該池塘的水體中注入含有氮磷的有害污水P，長期下來引發了池塘水體的富營養化，從而造成了該生物種群大量繁殖，進而使得池塘的水質變差。在有害污水的作用下，正常種群A中一些生物個體的基因會發生突變，從而演變出另外一種新種群，稱為突變種群B，其中的個體編號形成的集合為A2={1，2，…，Q2}。為了對該池塘的水體生態進行修復，環保部門定期投放一種微生物種群M。正常種群和突變種群，相互之間存在競爭關系，同一種群內部的個體是密度制約的。

正常種群和突變種群中的所有個體均可由n個特征描述，故種群類型u中的個體i可用來表示，其中是種群類型u中的個體i的特征j，i=1～Qu，j=1～n，u=1 表示正常種群，u=2 表示突變種群。

假設所要求解的優化問題為：

式中，F（X）為目標函數；S為解空間；X為n維解向量。在S中任意選擇Q1+Q2個試探解，即，其中，i=1～Qu，u=1～2，為解分量；池塘與S相對應，優化問題式（1）的Q1和Q2個試探解分別與Q1個正常種群與Q2個突變種群中的個體一一對應[9-10，16-19]。

在微生物種群M和化工廠排放的有害物質P的共同作用下，正常和突變種群中的個體的生長狀態會產生變化，該變化等價于試探解在解空間S中的空間位置變化[9-10，16-19]。

若某個體的目標函數值小，則該個體所處的空間位置較好，該個體適應度好，此類個體稱為強壯個體。反之，適應度差的個體稱為虛弱個體[9-10，16-19]。種群類型u中的個體i的強壯程度用個體強壯指數（individual physique index，ISI）來表示。強壯個體具有較高ISI值，虛弱個體具有較低的ISI值。種群類型u中的個體i的ISI指數按式（2）計算：

2.2 種群動力學模型

在受到污染的池塘水體中，具微生物治理和基因突變，且種群內部個體之間具有競爭關系的種群動力學模型（population dynamics model with microbial control and gene mutation and competition among individuals in contaminated environment，PDM-MCGMCICE）[11]如下所述：

其中，Q1（t）和Q2（t）分別表示正常種群和突變種群中的個體數量；P（t）表示每毫升水體中的污染物的量；M（t）表示每毫升水體中的微生物的量[11]；r為正常種群的增長率，r＞0；K1為環境容量，K1＞0；a1、b1、c1為正常種群和突變種群的競爭系數，則a1，b1，c1＞0；d為由于污染造成的正常種群的突變率，d＞0；d1為正常種群的自然死亡率，d1＞0；d2為突變種群的死亡率，d2＞0；d3是由于其他因素造成的污染物消除率，d3＞0 ；d4為微生物的衰亡率，d4＞0 ；q為污染物單位時間排放量，q＞0 ；μ是微生物生長率[11]，μ＞0；K2為半飽和常數，K2＞0；δ為產出率，δ＞0。為了保證正常種群和微生物種群的正增長，這里假設r＞d1[11]，μ＞d4。

為方便計算，將式（3）改為離散遞推形式，即：

2.3 特征個體集合的選擇方法

時期t，對當前種群類型u中個體i來說，其特征個體集合的生成策略如下：

（1）強壯個體集合SPu（t）。從Qu個個體中隨機選出ISI 指數比當前個體要高的L個個體，形成集合SPu（t）。L稱為特征個體數[9，19]。

（2）普通個體集合GPu（t）。從Qu個個體中隨機選出L個個體，形成集合GPu（t）[7-10，16-19]。

（3）虛弱個體集合WPu（t）。將Qu個個體按其ISI指數從小到大進行排列，形成虛弱個體排在前面、強壯個體排在后面的有序集合WPu（t）[9，19]。

2.4 正常和突變個體演化算子設計

PDO-MCCE 算法利用模型式（4）來構造演化算子，從而實現池塘水體中的有害物質P、微生物種群M、正常種群A和突變種群B之間的信息交換，進而實現對優化問題式（1）的求解。

（1）競爭算子。該算子描述的是正常和突變種群內部個體之間的競爭關系。將普通個體集合GPu（t）中種群類型為u的一些個體的某些特征s≠i，傳給種群類型為u的個體i，使該個體發生變化：

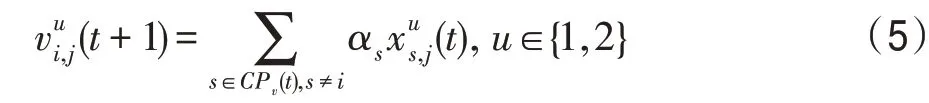
式中，αs=Rnd（-0.6，0.6）；和Rnd（a，b）含義參見文獻[19]。

（2）突變算子。該算子描述的是正常種群A中的個體在環境有毒因素P作用下發生基因突變，變成突變種群B中的個體。從正常種群個體集合A1中隨機選出一些個體直接發生類型改變，變為突變種群個體：

（3）影響算子。該算子描述的是正常或突變種群內部的一些強壯個體對同一種群內其他個體產生的影響。將種群類型為u的強壯個體集合SPu（t）中一些強壯個體的某些特征，傳給種群類型為u的個體i，使該個體受到同類中強壯個體的影響：

式中，βs=Rnd（0.3，0.5）。

（4）毒害算子。毒素算子的含義參加文獻[9]。對于種群類型為u的個體i來說，有：

式中，g1，g2，g3∈CPu（t），且g1≠g2≠g3。

（5）新生算子。該算子描述正常和突變種群中個體的新生。從種群類型為u的強壯個體集合SPu（t）和普通個體集合CPu（t）中各隨機選擇2 個個體進行組合，產生新生個體i：

式中，α=Rnd（0.4，0.6）。

（6）死亡算子。該算子描述正常和突變種群中個體的死亡。從種群類型為u的虛弱個體集合WPu（t）選擇排在最前面的個體，將其刪除。

（7）生長算子[9]。該算子描述的是個體的生長。對種群類型為u的個體i來說，生長算子定義如下：

2.5 PDO-MCCE 算法

步驟1初始化：（1）令t=0，設定演化時期數G、計算精度ε、Q1（0）、Q2（0）、個體特征發生變化的最高概率E0、特征個體數L、種群動力學模型參數r、a11、a12、b21、b22、d、d1、d2、d3、d4、q、μ、K1、K2、δ；（2）隨機確定、u=1～2、P（0）和M（0） ；（3）從中確定當前全局最優解Y*1。

步驟2執行下列操作：

2.6 算法特征分析

2.6.1 時間復雜度分析

表1 給出了PDO-MCCE 算法的時間復雜度計算過程[9，16，19]。

Table 1 Time complexity in PDO-MCCE（N=max（Q1+Q2））表1 PDO-MCCE 算法的時間復雜度（N=max（Q1+Q2））

2.6.2 PDO-MCCE 算法的收斂性分析

（1）Markov 特性。PDO-MCCE 算法的Markov特性分析可參見文獻[9，16，19]。

（2）“適應度遞增”特性。PDO-MCCE 算法的“適應度遞增”特性分析可參見文獻[9，16，19]。

（3）全局收斂性。PDO-MCCE 算法的全局收斂性證明可參見文獻[16]。

3 參數選擇

3.1 PDM-MCGMCICE 模型參數設置方法

文獻[11]對式（3）的平衡態的存在性和穩定性進行研究，得出如下結論：

定理1式（3）可能存在如下平衡態[11]：

定理2[11]對于式（3）來說，有：

從定理2 的（4）可知，當（r-d1）（μ-d4）＞dd4K2時，E4（Q1，Q2，P，M）能夠達到局部漸近穩定。也就是說，Q1、Q2、P、M的大小能夠趨于穩定。

由2.6.2 小節可知，PDO-MCCE 算法進行全局最優解搜索時，搜索過程具有Markov 特性。因此，搜索過程的Markov 隨機性保持得越持久，越不易陷入局部最優解陷阱。因此，PDM-MCGMCICE 模型參數r、a1、b1、c1、d、d1、d2、d3、d4、q、μ、K1、K2、δ的確定在滿足定理1 的第（4）條要求的同時，應保留足夠的隨機變化特性。

綜上所述，PDM-MCGMCICE 模型參數選擇只要按定理1的第（4）條的要求選取，就可使PDO-MCCE算法的搜索過程不易陷入局部最優解陷阱。

經過仔細篩選，可取r=Rnd（0.63，0.77），q=Rnd（9，11），μ=Rnd（0.135，0.165），d=Rnd（0.013 5，0.016 5），d1=Rnd（0.117，0.143），d2=Rnd（0.009，0.011），d3=Rnd（0.135，0.165），d4=Rnd（0.045，0.055），K1=Rnd（180，220），K2=Rnd（0.18，0.22），δ=Rnd（3.6，4.4），a1=0.000 1，b1=0.01，c1=0.000 1。此時，Q1=161.86，Q2=56.65，P=0.1，M=798.8。

應用上述取值策略，Q1、Q2、P、M的初始值分別設為100、50、5、200 時，利用式（3）可以計算出Q1、Q2、P、M隨時間的變化情況，如圖1 所示。從圖1可知，Q1、Q2、P、M具有極好的隨機性，且Q2還具有周期性突跳特征，有利于使搜索進程跳出局部最優解陷阱。

3.2 算法運行控制參數設置方法

（1）不要精確設置的參數G和ε。這兩個參數可按文獻[16]介紹的方法選取。

（2）關鍵參數E0、L。這兩個參數對算法性能影響較大，需要對其特性進行研究。

Bump 優化問題是一個極難求解的有約束優化問題，其特征與工程優化問題很相似，經常用來探明群智能算法的參數性能[16]。故本文以Bump 優化問題為例來探明E0、L的取值規律。Bump優化問題如下：

Fig.1 Randomness of Q1、Q2、P、M圖1 Q1、Q2、P、M 的隨機性

表2 描述了當L取不同值時，PDO-MCCE 算法求解Bump 優化問題所獲得的結果，計算參數為n=50，E0=0.01，G=108，運行50 次[9，16，19]。從表2 可知，L=3～7 為L的最佳取值區間[9，16，19]。

Table 2 Relationship of L with meanO and meanT表2 L 與meanO 和meanT 之間的關系

表3 描述了當E0取不同值時，PDO-MCCE 算法求解BUMP 優化問題所獲得的結果，計算參數為n=50，L=3，G=108，運行50 次[9，16，19]。從表3 可知，E0=0.006～0.100 為E0的最佳取值區間[9，16，19]。

Table 3 Relationship of E0 with meanO and meanT表3 E0 與meanO 和meanT 之間的關系

4 與其他算法比較

CEC2013[20]是國際上通用智能優化算法測試包，其中包括有28 個非常復雜的函數優化問題[9，16，19]，這些優化問題共分3 類，每類函數優化問題的特性可參見文獻[9，16，19]。本文在第1 類即單峰函數類選用F2 和F3，在第2 類即多峰函數類選用F15 和F19，在第3 類即組合函數類選用F21、F22 來測試PDOMCCE 算法的性能。

本文用PDO-MCCE算法去求解F2、F3、F15、F19、F21 和F22，其參數是n=50，G=108，ε=10-7，E0=0.01，L=3[9，16，19]。與PDO-MCCE算法進行比較的7 個智能優化算法均選自國際著名期刊近期刊登的知名算法[9]，這些算法是ABC（artificial bee colony）[3]、MpBBO（metropolis biogeography-based optimization）[4]、NP-PSO（non-parametric particle swarm optimization）[5]、RCGA（real-coded genetic algorithm）[21]、DASA（differential ant-stigmergy algorithm）[22]、Copt-aiNet（artificial immune net applied to distribution system reconfiguration with variable demand）[23]、SLADE（differential evolution with self-adaptive strategy and control parameters based on symmetric Latin hypercube design）[24]，這些算法的參數設置可參見相關文獻。這7 個算法的終止運行條件為：進化代數G=108或者最優解誤差ε=10-7[9，16，19]。

針對每個函數優化問題，每個參與比較的算法分別獨立運行51 次，以尋找全局最優目標函數[9-10，16，18-19]。表4 給出了每個算法所求得的最優目標函數值的平均值（Average）、中值（Median）、標準差（STD）、適應度評價次數（FE）、最優目標函數值的最小值（Min）與最大值（Max）[9-10，16，18-19]。8 個算法求解每個函數優化問題的性能排名Rank1 是基于Average 的精度進行的排名，Rank2 是基于Average 的精度和FE 進行的排名；Rank1 最終排名和Rank2 最終排名是分別基于Rank1 和Rank2 排名總積分而進行的排名。

從表4 可以看出這8 個參與比較的算法按Rank1和Rank2 的性能排序如下：

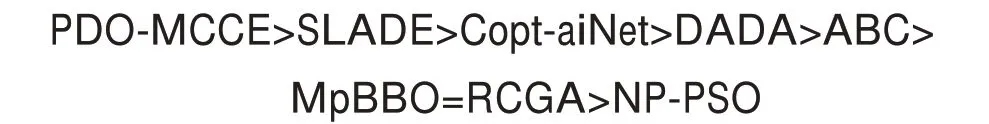
圖2（a）～（f）說明了各算法求解每個優化問題時的樣本收斂曲線。從表4 可知，PDO-MCCE 算法均能獲得理論全局最優解或以很高的精度發現全局最優解。

Table 4 Results of comparison calculation表4 對比計算結果

Fig.2 Convergence curves圖2 收斂曲線

5 求精、探索及其平衡性分析

（1）求精能力分析。從圖2（a）～（f）知，與7 個被比較算法相比，PDO-MCCE 算法的收斂曲線在一些時間段內上升較慢且持續時間長，表明該算法提升最優解精度的過程十分明確。該特征說明PDOMCCE 算法的求精能力比7 個被比較算法強[7-10，16-19]；從表4 知，PDO-MCCE 算法求解F2、F3、F15、F19、F21、F22 時，均能獲得其理論全局最優解，此說明PDO-MCCE 算法比7 個被比較算法具有更好的求精能力[7-10，16-19]。

（2）探索能力分析。從圖2（a）～（f）知，與7 個被比較算法相比，PDO-MCCE 算法的收斂曲線在一些時間段內較陡且持續時間短，表明該算法提升ISI 指數的耗時很短。該特征說明PDO-MCCE 算法比7 個被比較算法具有更好的探索新空間的能力[7-10，16-19]。

（3）求精和探索能力的平衡性分析。從圖2（a）～（f）可知，與7 個被比較算法相比，PDO-MCCE 算法的緩（求精能力）和陡（探索能力）交替出現，且緩的持續時間均較長，陡的持續時間均較短，此表明PDOMCCE 算法的求精和探索能力的平衡性均優于7 個被比較算法[7-10，16-19]。

6 結束語

本文基于PDM-MCGMCICE 模型提出了一種具有全局收斂性的新型優化算法，與其他典型群智能算法相比，PDO-MCCE 算法具有如下特點：

（1）個體被自動劃分成2 類，每類個體數依據PDM-MCGMCICE 模型自動進行調整，增加了個體的多樣性，解決了人為確定個體數的難題。

（2）所有算子是通過利用PDM-MCGMCICE 模型以及種群間和種群內的個體間的相互作用關系來進行構造的，不需要與要求解的實際優化問題相關。因此，PDO-MCCE 算法具有很好的普適性[7-10，16-19]。

（3）PDO-MCCE 算法中的每個算子具有明確功能，其中競爭算子和突變算子分別可實現種群內和種群間個體的信息交換；而影響算子可實現種群內強壯個體的信息擴散[7-10，16-19]；毒害算子可將環境信息傳遞給不同種群內的個體，使其受到環境的影響；新生算子可增加強壯個體數；死亡算子可以減少虛弱個體數；生長算子可確保算法具有全局收斂性。

（4）突變種群內的個體數的周期性突然增加，有利于大量強壯個體突然參與搜索，從而可大幅增加搜索進程跳出局部最優解陷阱的概率。

（5）采用PDM-MCGMCICE 模型的機理確定PDO-MCCE 算法中的相關參數，大幅減少了該算法參數的人工確定個數。實際上，PDO-MCCE 算法需要人工確定的參數只有2 個。

（6）由于每個時期只有3/500～1/10 的個體特征參與計算，導致PDO-MCCE 算法的時間復雜度大幅降低，因此該算法適于求解高維復雜優化問題。

PDO-MCCE算法未來需要深入研究的問題如下：

（1）深入研究各算子的動態特征；

（2）深入研究各種群的動態特征。