數學因其他學科融入而精彩

福建 湯小梅 鄭金木

數學與其他學科的交匯與融合是近幾年高考中經常出現的現象，此類試題常常以“新交匯”為載體，體現了“返璞歸真，支持課改，突破定勢，考查真功”的命題理念，意在考查數學建模、數學抽象、數據分析、直觀想象、邏輯推理和數學運算等核心素養，值得重點關注．現以2020年各省市模擬題為例，對數學與其他學科的交匯型考題進行歸納，感悟數學知識與其他學科之間的關聯，加強對數學交匯性的理解，旨在揭示命題動向與解題策略，以期能為讀者提供幫助．

一、音樂中的數學

音樂的要素——音高、音色、節拍、樂音、樂曲、樂器等都與數學相關，特別是音的律制與數學的關系十分密切．以音樂為背景的考題，可以讓學生更加理性地理解音樂、鑒賞音樂的美，增強理性思維能力，提升學生的數學素養．常見考法有：聲波與正弦函數結合，律制、音階與數列結合，樂曲的節拍與分數結合，樂器中的數學，樂曲中的數學等．

【典例1】(2020·廣東省深圳市羅湖區高三質量檢查)中國古代的五音，一般指五聲音階，依次為：宮、商、角、徵、羽；如果把這五個音階全用上，排成一個五個音階的音序，且要求宮、羽兩音階在角音階的同側，可排成多少種這樣的不同音序( )

A．120 B．90 C．80 D．60

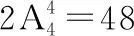
【方法點津】本題以音樂學科中的“音階”為載體考查排列組合應用問題，破解此類題的關鍵：一是有限制條件的元素需優先考慮，如本題，需對限制條件“宮、羽兩音階在角音階的同側”優先考慮，分類的“度”就很明確，只需對“角音階”的位置進行分類；二是會利用排列組合的應用情況進行求解，有序用排列，無序用組合．

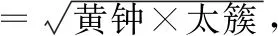
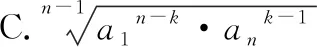
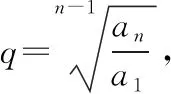
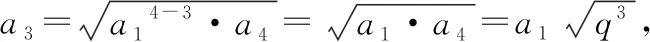
【方法點津】本題以音樂學科的“音的律制”為載體考查等比數列與類比推理等基礎知識.破解此類題的關鍵：一是讀懂題目的文化背景，如本題，需讀懂“等程律”；二是利用等比數列的通項公式進行等價變形求解．若會利用特取法，如解法二，即可把一般性的繁雜的推導，轉化為數列前4項之間的關系式的推導，從而達到窺斑知豹之功效．

二、美術中的數學

美術主要包括繪畫、雕塑、工藝美術、建筑藝術，以及書法、篆刻等，美術中的平移、對稱、黃金分割、幾何透視等都與數學相關．以美術為背景的考題，可以讓學生了解在美術家的創作過程中所蘊含的數學思想，體會數學在美術中的作用，更加理性地鑒賞美術作品，提升直觀想象、數學抽象、數學運算的核心素養．常見考法有：名畫中的數學元素、繪畫中的平移與對稱、雕塑、書法、建筑、繪畫中的黃金分割、工藝品中的對稱等．

【典例3】(2020·遼寧省實驗中學期中)素描是學習繪畫的必要一步，它包括了明暗素描和結構素描，而學習幾何體結構素描是學習素描最重要的一步．某高中2018級同學在畫“切面圓柱體”(用與圓柱底面不平行的平面去截圓柱，底面與截面之間的部分叫做切面圓柱體)的過程中，發現“切面”是一個橢圓，若“切面”所在平面與底面成60°角，則該橢圓的離心率為( )

【方法點津】本題以美術學科的“素描”為載體考查空間幾何體的結構、線面角與橢圓的幾何性質等基礎知識.有關此類多交匯點試題，求解的關鍵：一是明晰空間幾何體的結構特征；二是活用定義，即會利用空間線面所成角的定義，得到橢圓的長軸長、短軸長的關系式；三是應用公式，即會利用橢圓的離心率公式，得出結果．

三、體育中的數學

在體育運動中，無論是運動本身還是與運動有關的事都蘊含著許多數學原理．以體育為背景的考題，可以讓學生運用數學知識探索提高運動效率的途徑，能運用數學方法合理安排賽事，增強理性思維能力，提升直觀想象、數學抽象和數學運算的核心素養．常見考法有：運動場上的數學原理考查向量知識；運動成績的數據分析考查概率與統計知識；借助圖象、運籌等數學知識分析體育賽事的規律，改善運動員賽場上的應對策略；體育用具及設施中也蘊含數學知識，如足球、乒乓球的制作，網球拍的構造，考查的是空間幾何體問題，等等．

【典例4】(2020·安徽省蚌埠市高三第三次教學質量檢查)足球起源于中國東周時期的齊國，當時把踢足球稱為“蹴鞠”.漢代蹴鞠是訓練士兵的手段，制定了較為完備的體制，如專門設置了球場，規定為東西方向的長方形，兩端各設六個對稱的“鞠域”，也稱“鞠室”，各由一人把守.比賽分為兩隊，互有攻守，以踢進對方鞠室的次數多少決定勝負.1970年以前的世界杯用球多數由舉辦國自己設計，所以每一次球的外觀都不同，拼塊的數目如同擲骰子一樣沒準.自1970年起，世界杯官方用球選擇了三十二面體形狀的足球，沿用至今.如圖Ⅰ，32面體足球的面由邊長相等的12塊正五邊形和20塊正六邊形拼接而成，形成一個近似的球體.現用邊長為4.5cm的上述正五邊形和正六邊形所圍成的三十二面體的外接球作為足球，其大圓圓周展開圖可近似看成是由4個正六邊形與4個正五邊形以及2條正六邊形的邊所構成的圖形的對稱軸截圖形所得的線段AA′，如圖Ⅱ，則該足球的表面積約為( )

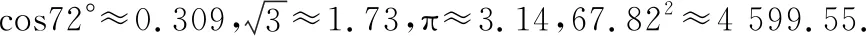
A．366.64cm2B．488.85cm2

C．1 464.82cm2D．5 282.40cm2

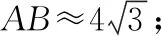
【方法點津】本題以體育學科的體育用具“足球”為載體考查空間幾何體的結構、表面積和余弦定理等基礎知識.此類題求解的突破口：一是細審題和細觀圖，認真讀懂題意，并能觀察出幾何體的結構特征，畫出草圖；二是活用定理，即會利用余弦定理求出線段的長；三是應用公式，會利用圓的周長公式和球的表面積公式求出相應的量．

四、化學中的數學

化學是數學天生的載體，以化學為背景的考題，可以拓展視野，提升邏輯推理、數學運算、直觀想象、數學建模等核心素養．常見考法有：以溶液濃度為背景創設的數列、函數等問題，以化學中的分子等為背景創設的空間幾何體的結構特征、表面積或體積的問題，以化合物的結構式及分子式創設的歸納推理問題，等等．

【典例5】(2020·河南省期中測試)甲、乙兩容器中分別盛有兩種濃度的某溶液300ml，從甲容器中取出100ml溶液，將其倒入乙容器中攪勻，再從乙容器中取出100ml溶液，將其倒入甲容器中攪勻，這稱為一次調和，已知第一次調和后，甲、乙兩種溶液的濃度分別記為a1=20%,b1=2%,第n次調和后的甲、乙兩種溶液的濃度分別記為an,bn.

(1)請用an,bn分別表示an+1和bn+1；

(2)問經過多少次調和后，甲、乙兩容器中溶液的濃度之差小于0.1%.

【解析】(1)由題意可知甲、乙兩種溶液第一次調和后的濃度分別為a1=20%,b1=2%，

(2)由于題目中的問題是針對濃度之差，所以我們不妨直接考慮數列{an-bn}．

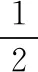
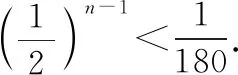
【方法點津】解決此類以化學的溶液濃度為背景的數列模型題的關鍵：一是認真審題，構建數列模型，如本題，構建兩個數列模型；二是解模，即根據題意，把所求的問題轉化為已知兩個數列的遞推公式，求解不等式問題，通過等比數列定義的應用，以及解指數不等式，即可求得結果．

【典例6】(2020·重慶巴蜀中學高三月考)已知C60分子是一種由60個碳原子構成的分子，它形似足球，因此又名足球烯，C60是單純由碳原子結合形成的穩定分子，它有60個頂點和若干個面.各個面的形狀為正五邊形或正六邊形，結構如圖.已知其中正六邊形的面為20個，則正五邊形的面的個數為( )

A．10 B．12 C．16 D．20

【方法點津】解決此類以化學C60分子為背景的立體幾何模型題的關鍵：一是認真讀題，構建立體幾何模型，如本題，構建空間多面體模型；二是解模，即根據題意，把所求的問題轉化為求幾何體的正五邊形的面數問題．

【典例7】(2020·安徽師范大學附屬中學高二期中)按照下列三種化合物的結構式及分子式的規律，寫出后一種化合物的分子式( )

A．C4H9B．C4H10

C．C4H11D．C6H12

【解析】依題意可知，后一個分子式總比前一個分子式多1個C和2個H，所以第四種化合物的分子式為C4H10，故選B.

【方法點津】本題以化學學科的“化合物的結構式”為載體，考查歸納推理等基礎知識.像這樣由一系列有限的特殊結論來歸納得出一般結論的推理就是歸納推理.一般地說，“求同存異”“逐步細化”“先粗后精”是求解由特殊結論推廣到一般結論型創新題的基本技巧．

五、物理中的數學

數學與物理不分家，以物理為背景的考題，可以提升邏輯推理、數學運算、直觀想象、數學建模等核心素養．常見考法有：以天體運動為背景(如衛星的運行軌跡等)考查橢圓的幾何性質，以物理中的“質量等于體積與密度之積”的計算考查幾何體的體積，以分子間作用力創設函數與方程問題，等等．

【典例8】(2020·新疆烏魯木齊地區高三年級第一次質量監測)天文學中為了衡量星星的明暗程度，古希臘天文學家喜帕恰斯(Hipparchus，又名依巴谷)在公元前二世紀首先提出了星等這個概念.星等的數值越小，星星就越亮；星等的數值越大，它的光就越暗.到了1850年，由于光度計在天體光度測量中的應用，英國天文學家普森(M.R.Pogson)又提出了衡量天體明暗程度的亮度的概念.天體的明暗程度可以用星等或亮度來描述.兩顆星的星等與亮度滿足m1-m2=2.5(lgE2-lgE1).其中星等為mi的星星的亮度為Ei(i=1,2).已知“心宿二”的星等是1.00，“天津四” 的星等是1.25，“心宿二”的亮度是“天津四”的r倍，則與r最接近的是( )(當|x|較小時，10x≈1+2.3x+2.7x2)

A．1.24 B．1.25 C．1.26 D．1.27

六、地理中的數學

地理學科中的常識問題，常常作為數學創新問題的載體，可以提升數學抽象、邏輯推理、數學運算、直觀想象、數學建模等核心素養．常見考法有：以地理位置背景考查空間幾何體的空間角問題或解三角形問題．

【典例9】(2020·河南省名校(南陽一中、信陽、漯河、平頂山一中四校)高三3月線上聯考)小王想在某市一住宅小區買套新房，據了解，該小區有若干棟互相平行的平頂樓房，每棟樓房有15層，每層樓高為3米，頂樓有1米高的隔熱層，兩樓之間相距60米.小王不想買最前面和最后面的樓房，但希望所買樓層全年每天正午都能曬到太陽.為此，小王查找了有關地理資料，獲得如下一些信息：①該市的緯度(地面一點所在球半徑與赤道平面所成的角)為北緯36°34′；②正午的太陽直射北回歸線(太陽光線與赤道平面所成的角為23°26′)時，物體的影子最短，直射南回歸線(太陽光線與赤道平面所成的角為-23°26′)時，物體的影子最長，那么小王買房的最低樓層應為( )

A．3 B．4 C．5 D．6

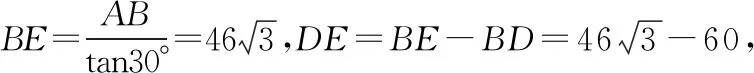
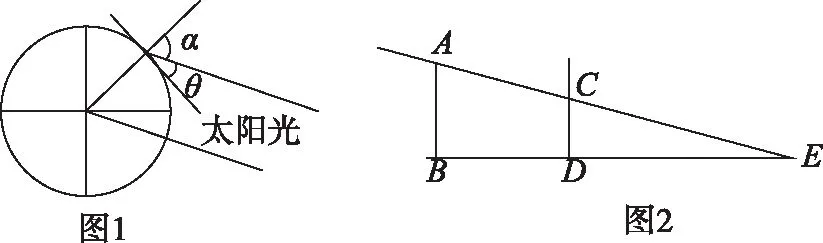
【方法點津】本題以地理學科為載體考查解三角形等基礎知識，破解此類題的關鍵：一是準確理解題意，獲取有效信息；二是根據題意畫出其示意圖，示意圖起著關鍵的作用；三是解三角形，掌握直角三角形的特征，通過合理運算，即可得出結果．

七、醫學中的數學

以醫學為背景的數學考題，展示了跨界的精彩，體現了數學在實際生活中的應用，可以提升邏輯推理、數學運算、直觀想象、數學建模、數學分析等核心素養．常見考法有：以醫學中的藥物等為背景創設函數圖象、函數模型、統計分析等數學問題．

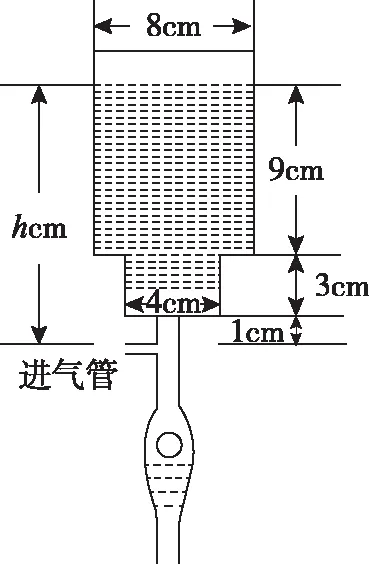
【典例10】(2020·襄陽市襄州區第一高級中學期中)2019年諾貝爾生理學或醫學獎獲得者威廉·凱林(William G.Kaelin Jr)在研究腎癌的VEGF抑制劑過程中使用的輸液瓶可以視為兩個圓柱的組合體.開始輸液時，滴管內勻速滴下液體(滴管內液體忽略不計)，設輸液開始后x分鐘，瓶內液面與進氣管的距離為h厘米，已知當x=0時，h=13.若瓶內的藥液恰好156分鐘滴完.則函數h=f(x)的圖象為( )

【方法點津】解決此類以醫學為背景的函數圖象判斷題的關鍵：認真讀懂題意，明晰幾何體的特征，根據題意，求出函數的解析式，即可判斷函數的單調性，從而判斷函數的圖象特征，即可得出正確的選項．

A．22藥物單位 B．20藥物單位

C．12藥物單位 D．10藥物單位

【方法點津】解決此類以藥物功效為背景的用樣本估計總體題型的關鍵：一是讀懂題意，明晰已知的量與需求解的量；二是活用公式，即會利用平均數、方差和標準差的公式，即可得結果．