共焦點的橢圓與雙曲線的性質探究

重慶 劉紫陽

在有關解析幾何的問題中，常常涉及具有共同焦點的橢圓與雙曲線，通過筆者的研究發現，它們具有如下性質.

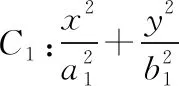
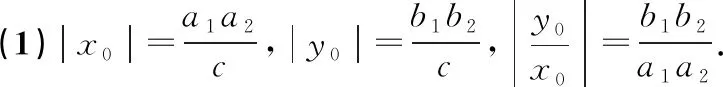
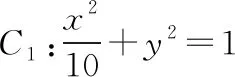
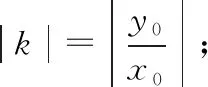
評注：在涉及有關共焦點的橢圓與雙曲線的公共點坐標問題時，可考慮聯系此性質來幫助解決.

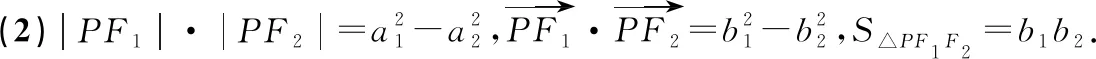
兩式分別平方再相減得4|PF1|·|PF2|=

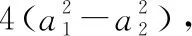
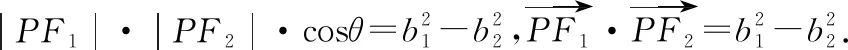
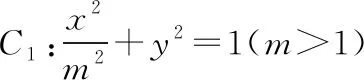
分析：一種思路是根據題意聯想到橢圓與雙曲線的焦點三角形面積公式得出結論；另一種思路是聯系到上述性質，焦點三角形的面積公式S△PF1F2=b1b2得出結論.

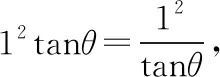
解法2：依題意與性質一(2)得知，△PF1F2的面積為1×1=1.

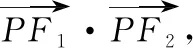
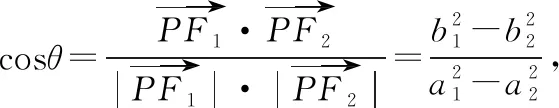
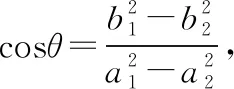
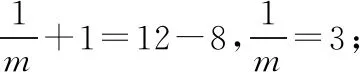
評注：在涉及有關共焦點的橢圓與雙曲線的公共點P與F1,F2連線的夾角問題時，可借助此性質來幫助解決.

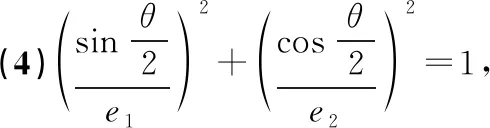
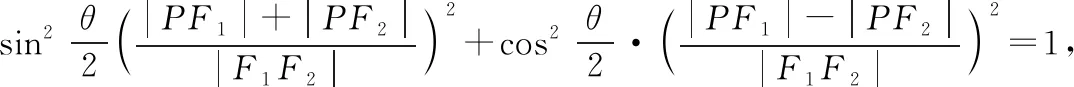
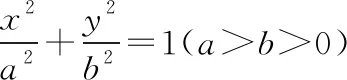
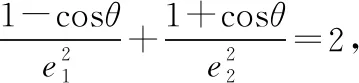
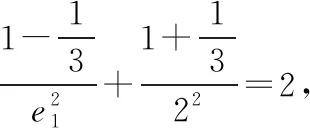
評注：在涉及有關共焦點的橢圓與雙曲線的離心率問題時，可借助此性質來幫助思考.

性質(5)曲線C1與C2在點P(x0,y0)處的切線相互垂直.

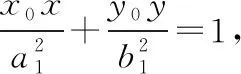
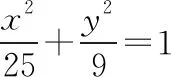
評注：在涉及有關共焦點的橢圓與雙曲線在其公共點處的切線問題時，可借助此性質來幫助思考.

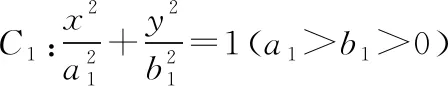
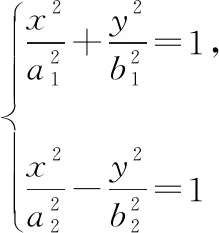
分析：根據題意與性質二得知，題中的橢圓與雙曲線有共同的焦點，利用橢圓與雙曲線a,b,c間的關系得出結論.

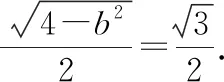
評注:在涉及有關共焦點的橢圓與雙曲線在其公共點處的切線相互垂直的問題時，可考慮應用此性質，得出其焦點相同，由此解決問題.