“四能”驅(qū)動培育核心素養(yǎng),從容助力應對新高考
山東 李化周
2019年的全國高考數(shù)學新課標卷Ⅰ引起了社會的廣泛關(guān)注,許多考生感覺不適應.2020年高考數(shù)學又進行了改革,增加了4道多選題,題量與思維量增大,對學生的應考能力提出了更高的要求.新的課程標準提出要提升學生素養(yǎng),注重發(fā)展學生應用實踐能力與創(chuàng)新能力,而素養(yǎng)目標會逐漸落實于高考中.作為數(shù)學教師應精準把握高考的改革方向,在日常的教學中滲透數(shù)學思想,培育學生數(shù)學核心素養(yǎng),提升學生數(shù)學解題能力.在教學中數(shù)學教師應改變以往偏重直接傳授知識的方式,多創(chuàng)設(shè)學科情境,通過組織學科活動,引導學生主動去發(fā)現(xiàn)、去經(jīng)歷、去感悟.教師應更多地在學生無疑處生疑、無向處指向、無力時借力,讓學生站在課堂的正中央.如何幫助學生更從容地走過高考呢?經(jīng)過筆者所在學校高三數(shù)學組近一年的探索,發(fā)現(xiàn)在平時的數(shù)學教學中應注重學生四個方面能力的培養(yǎng):數(shù)據(jù)分析能力、模型構(gòu)建能力、數(shù)學運算能力、閱讀理解能力.
一、強化學生數(shù)據(jù)分析能力
數(shù)據(jù)分析是大數(shù)據(jù)時代數(shù)學應用的主要方法,過程主要包括:收集數(shù)據(jù)、整理數(shù)據(jù)、提取信息、構(gòu)建模型、進行推斷、獲得結(jié)論.學生的數(shù)據(jù)分析能力也是近幾年高考考查的重點.教學中要側(cè)重利用圖象、表格、頻率分布直方圖、條形圖、餅形圖、折線圖、莖葉圖等培養(yǎng)學生識表讀圖能力,培養(yǎng)學生對收集的數(shù)據(jù)進行再處理、再分析的能力.
【例1】相關(guān)變量x,y的散點圖如圖所示,現(xiàn)對這兩個變量進行線性相關(guān)分析.


A.0 C.-1 從圖象上,我們發(fā)現(xiàn)(10,26)這個數(shù)據(jù)與其他數(shù)據(jù)差別較大,可能在數(shù)據(jù)收集過程中出現(xiàn)了誤差,我們可以剔除掉(10,26),再來研究規(guī)律.發(fā)現(xiàn)這些數(shù)據(jù)呈現(xiàn)負相關(guān)特性,剔除問題數(shù)據(jù)后,相關(guān)性增強,即r2更接近-1,故選C. 發(fā)展學生數(shù)據(jù)分析能力,在教學中一是可以借助信息技術(shù),提升學生數(shù)學理解能力.教師借助信息技術(shù)多創(chuàng)設(shè)學生感興趣的情境,激發(fā)學生探究興趣;二是開展豐富的實踐活動,引導學生經(jīng)歷數(shù)據(jù)收集、整理、分析和預測的過程.讓學生利用R軟件、Geogebra、excel表格、spass等工具分析數(shù)據(jù),改變數(shù)據(jù)呈現(xiàn)方式,增強學生抽象理解能力同時也可以很好地鍛煉學生的分析能力,豐富學生處理數(shù)據(jù)的方法. 新課標強調(diào)數(shù)學融于生活,讓學生從生活中提出數(shù)學問題,應用數(shù)學知識解決生活中的問題.新教材設(shè)計了多個數(shù)學建模的環(huán)節(jié),使數(shù)學建模落實于課堂.在試卷中主要以應用題的形式考查,學生需要從問題中識別出數(shù)學模型,然后利用數(shù)學的方法解決問題. 在數(shù)學教學中可以在以下方面培養(yǎng)學生數(shù)學建模能力:一是引導學生關(guān)注生活,對生活中的現(xiàn)象進行分析,發(fā)現(xiàn)其中蘊含的數(shù)學問題,嘗試用數(shù)學方法解答.知識來源于生活,生活中蘊含著豐富的數(shù)學模型,要引導學生養(yǎng)成從生活中尋找問題的習慣;二是讓課堂開放,鼓勵學生在課堂上提出問題,在思考、合作、交流中找到問題的答案;三是鼓勵學生們通過觀察將生活和教材上的知識進行連接,學會相互聯(lián)系;四是教師要經(jīng)常滲透模型構(gòu)造的方法.常用的構(gòu)造方法有將實際問題轉(zhuǎn)化成方程問題、將實際問題轉(zhuǎn)化成函數(shù)問題、將實際問題轉(zhuǎn)化成圖形問題、將實際問題轉(zhuǎn)化成三角問題、向量問題、不等式問題等. 運算能力是思維和技巧的結(jié)合,包括對數(shù)值的準確計算和估算, 對數(shù)學表達式的變形與轉(zhuǎn)化等,運算過程中要認清運算條件、明確運算方向、選擇運算公式、確定運算程序等;也包括在實施運算過程中遇到障礙而調(diào)整運算策略的能力,以及堅持到底的韌性.在運算教學中,教師應該多關(guān)注學生思維品質(zhì)的培養(yǎng),使學生終身受用. A. 165cm B. 175cm C. 185cm D. 190cm 按以往的經(jīng)驗,在試卷這個位置的題目學生應該非常輕松地可以完成,但很多學生在這個題就卡住了.據(jù)學生考完后反映,一部分學生讀不懂題意,有點懵;一部分學生沒有注意到關(guān)鍵詞“可能是”,這部分學生沒有嘗試估算而執(zhí)著于直接求得準確的答案; 還有相當一部分學生根據(jù)生活中的經(jīng)驗憑直覺選出了正確答案B. 在新的高考形式下,學生文本理解能力、生活經(jīng)驗等對考生考場作答影響較大.在教學中,教師應多引導學生以數(shù)學的眼光觀察世界,多了解生活中的數(shù)學,了解數(shù)學歷史,體會數(shù)學精神,感悟數(shù)學思想. 【例5】(2019·全國卷Ⅰ理·21)為治療某種疾病,研制了甲、乙兩種新藥,希望知道哪種新藥更有效,為此進行動物試驗.試驗方案如下:每一輪選取兩只白鼠對藥效進行對比試驗.對于兩只白鼠,隨機選一只施以甲藥,另一只施以乙藥.一輪的治療結(jié)果得出后,再安排下一輪試驗.當其中一種藥治愈的白鼠比另一種藥治愈的白鼠多4只時,就停止試驗,并認為治愈只數(shù)多的藥更有效.為了方便描述問題,約定:對于每輪試驗,若施以甲藥的白鼠治愈且施以乙藥的白鼠未治愈則甲藥得1分,乙藥得-1分;若施以乙藥的白鼠治愈且施以甲藥的白鼠未治愈則乙藥得1分,甲藥得-1分;若都治愈或都未治愈則兩種藥均得0分.甲、乙兩種藥的治愈率分別記為α和β,一輪試驗中甲藥的得分記為X. (Ⅰ)求X的分布列; (Ⅱ)若甲藥、乙藥在試驗開始時都賦予4分,pi(i=0,1,…,8)表示“甲藥的累計得分為i時,最終認為甲藥比乙藥更有效”的概率,則p0=0,p8=1,pi=api-1+bpi+cpi+1(i=1,2,…,7),其中a=P(X=-1),b=P(X=0),c=P(X=1).假設(shè)α=0.5,β=0.8. (i)證明:{pi+1-pi}(i=0,1,2,…,7)為等比數(shù)列; (ii)求p4,并根據(jù)p4的值解釋這種試驗方案的合理性. 這個題目如果改動一下,單獨作為數(shù)列題進行考查:若數(shù)列{an}滿足:an=0.4an-1+0.5an+0.1an+1,且a1=0,a9=1,求證:{an+1-an}為等比數(shù)列,并求a5. 由an=0.4an-1+0.5an+0.1an+1很容易得到0.1(an+1-an)=0.4(an-an-1),進而可以證得{an+1-an}為等比數(shù)列,并借助a1=0,a9=1求得a5的值.而題目中a,b,c的值學生并不難求出.學生感覺考場乏力有以下幾個因素:一是閱讀能力不足,不能在有限時間內(nèi)讀懂題意;二是生活經(jīng)驗匱乏,不能準確理解各字母含義,不能準確全面地分析可能會發(fā)生的各種情況;三是數(shù)學建模能力薄弱,不能從題中發(fā)現(xiàn)、抽象出數(shù)學模型;四是對多符號、多字母式子不能靜心分析每一個字母、符號代表的含義,失去了作答的信心. 【例6】窗的運用是中式園林設(shè)計的重要組成部分,常常運用象征、隱喻、借景等手法,將民族文化與哲理融入其中,營造出廣闊的審美意境.如圖,在平面直角坐標系xOy中,O為正八邊形P1P2…P8的中心,P1P8⊥x軸,現(xiàn)用如下方法等可能地確定點M:PiPj(其中1≤i,j≤8,且i,j∈N*,i≠j)是正八邊形的頂點,M為線段PiPj的中點,則點M(異于點O)落在坐標軸上的概率為( ) 這是一道融合了中國傳統(tǒng)文化的創(chuàng)新題,字母較多,看似毫無頭緒,仔細觀察就可發(fā)現(xiàn)若點M在坐標軸上,則Pi與Pj必關(guān)于坐標軸對稱,即問題轉(zhuǎn)化成軸對稱問題.從8個點中任取兩個點共有28種取法,而Pi與Pj關(guān)于x軸對稱的有4對,Pi與Pj關(guān)于y軸對稱的也有4對,共8對,根據(jù)古典概型概率公式可以求得D選項正確.二、積極培養(yǎng)學生模型構(gòu)建能力


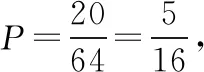

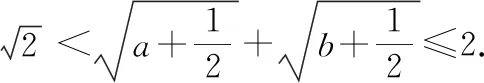



三、培養(yǎng)學生數(shù)學運算能力

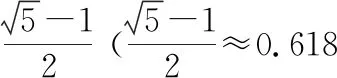
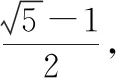
四、大力培養(yǎng)學生閱讀理解能力



