基于Runge-Kutta法的輸氣管道泄漏定位技術研究

吳波 楊旭東 張小芳 司宗慶 牟燕 梁昌晶

1中國石油華北油田公司第三采油廠

2中國石油華北油田公司第一采油廠

3中國石油華北油田公司二連分公司

輸氣管道的泄漏定位技術是管道完整性管理的重要組成部分，管道防腐層的缺失、陰極保護的失效、土壤介質對管道外壁的腐蝕，以及管輸介質對管道內壁產生的腐蝕，均會引起管道不同程度的泄漏[1]。據統計，1995—2005 年，中國石油管道分公司每年大約產生12～15 起重大輸氣管道泄漏事故，其中2004 年因腐蝕引起的管道泄漏事故就多達20余起[2-3]。目前，已有多種針對管道泄漏的檢測與定位技術，但每種檢測方法的原理和手段差別較大，同時由于管輸天然氣組分的多樣性，敷設方式的差異性（如埋地、直敷、架空、穿跨越等），以及泄漏方式的多元性（如滲透、穿孔、斷裂等），使得各種檢測方法在定位精度和檢測時間上都存在一定的局限性[4-5]。

韓玲娟等[6]采用分布式光纖傳感器對水下輸氣管道的泄漏進行了有效定位，采用小波神經網絡對信號進行了有效提取，用聚類分析判斷管道泄漏的嚴重程度，并采用最小二乘法擬合信號參數進行定位，該方法與傳統定位方法相比誤報率下降了6.6%；焦敬品等[7]通過對20種不同的泄漏信號進行識別，運用BP 神經網絡進行泄漏點的檢測和定位，整體識別率≥92.5%；田野[8]設計了一套基于次生波原理的泄漏監測系統，結合了比例-積分-微分（PID）整定調節和自適應算法，對輸氣管道的泄漏定位誤差≤20 m；李鳳等[9]將負壓波和聲波技術進行了耦合，通過前處理軟件（ICEM）對管道進行了網格劃分，應用計算流體力學（CFD）軟件進行了流場變化分析，有效解決了單一信號噪聲大、魯棒性差的缺點。綜上所述，管道的定位檢測需要在首末點設置大量的傳感器，并且采用多種軟件進行模型構建和數據模擬，工作量大，一般操作人員較難掌握。

我國大部分輸氣管道由于管道沿程高差的區別和地理跨度的差異，屬于非等溫輸氣管道，隨著計算機科學和數值分析理論的不斷發展，通過現有傳感器測量的溫度、壓力和流量數據，采用改進的變步長龍格-庫塔（Runge-Kutta）法對非等溫輸氣管道進行檢測和定位，同時通過實例進行仿真計算，并與傳統的負壓波檢測結果進行對比，以期可以快速、準確地對泄漏點進行定位。

1 模型建立

1.1 輸氣管道模型

將輸氣管道中介質的流動視為穩態流動，而穩態流動與時間變量無關，根據流體力學和熱力學相關公式建立沿管輸方向的穩態流動方程[10-11]。其中連續性方程、動量方程、能量方程和狀態方程分別為

式中：ρ為管輸氣體密度，kg/m3；ω為氣體流速，m/s；x為管道長度，m；p為管輸氣體壓力，Pa；g為重力加速度，取9.8 m/s2；θ為管道傾角，rand；λ為水力摩阻系數；d為管道內徑，m；h為管輸氣體的焓，J/kg；s為管道的位置高度，m；Q為單位質量氣體向外界釋放的能量，J/kg；T為管輸氣體溫度，K。

在已知氣體組分及溫度、壓力的前提下，可以由實際氣體狀態方程對氣體密度和壓縮系數進行求解，比較實用的狀態方程有RK、SRK、BWRS 和PR方程，在此采用BWRS方程進行計算[12]。

1.2 Runge-Kutta法

該算法是一種在工程上被廣泛應用的高精度單步算法，主要原理是通過對常微分方程組進行離散化處理，求解該方程的初值；隨后選擇不同的步長，在之間計算多個點的斜率值，將其加權平均作為平均斜率。為了便于計算，通常采用較為經典的四階Runge-Kutta 進行計算[13]，通過與泰勒級數展開式進行對比后求解未知數，簡化后的公式如下

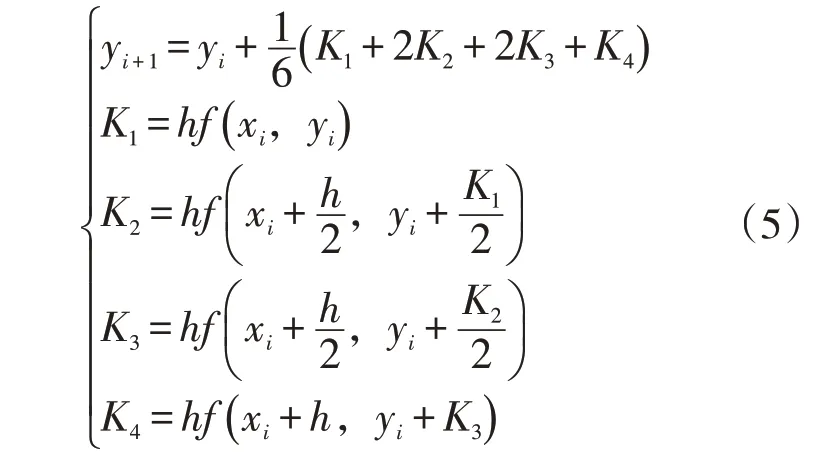
式中：xi、yi分別為自變量和因變量；yi+1為下一個步長的因變量；h為步長系數；K1、K2、K3、K4為待定系數，表示輸出變量的一階倒數。

將管道分成n段，每段管道長度定為Δx（代表每段管道的微元）。Runge-Kutta法的關鍵是對于Δx的合理選擇，單從每一個截斷來看，步長越小，截斷誤差越小，但隨著步長的不斷減少，計算時間也在不斷延長，一定范圍內的求解步數也會增加。不同的迭代計算會導致舍入誤差的大量累計，在計算效率和精度上有很大缺陷，因此首先設置較大的計算步長，在整個管段內進行泄漏位置的初選，隨后逐步縮小泄漏定位的搜索范圍，直到滿足定位精度的要求，一般取0.5%～1%的初始步長進行運算。

在經典四階Runge-Kutta 算法的基礎上采用精細Runge-Kutta 法計算，該方法融合了精細積分法和Runge-Kutta 法的優點，可以將特解的數值代入Runge-Kutta公式中積分，并利用Runge-Kutta法對數值積分點的未知參數進行預估，得到更精細的算法。根據現場傳感器采集到的管道起點溫度Ti、壓力pi和流量mi，計算從起點到末點管道各截面的溫度、壓力和流量數值。首先計算第一個微元Δx1的斜率k1，從第一個積分點出發，前進半個步長，得到第二個積分點的預測斜率k2；然后以k2為基礎，再次從第一個積分點出發，前進半個步長，重新計算第二個積分點的預測斜率k′2；將兩次計算的k2和k′2進行加權平均，作為第二個積分點的近似斜率；以此類推，直到計算出最后一個積分點也就是管道末點的溫度、壓力和流量數值。其中以第一個微元管道Δx1為例，運用Runge-Kutta法求解公式（1）～（4）來計算管道截面的參數，公式如下

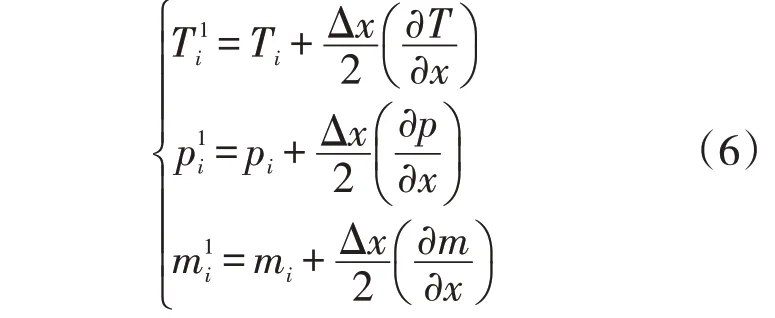
以此類推，得到管道末點的溫度Ti+1、壓力pi+1和流量mi+1的計算公式如下

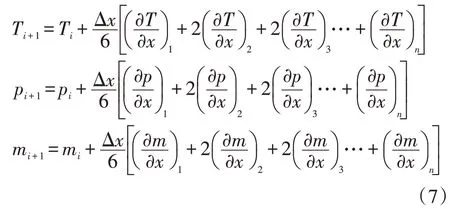
從管道起點開始，運用Matlab 對公式（7）進行反復的迭代計算，即可完成從管道起點到末點不同截面的溫度、壓力和流量的計算；從末點到起點的參數計算也類似，只是將公式（2）～（3）的摩擦阻力項和熱損失項進行調整，具體見式（8）～（9），這種模型非常適合非等溫輸氣管道的模擬和仿真。

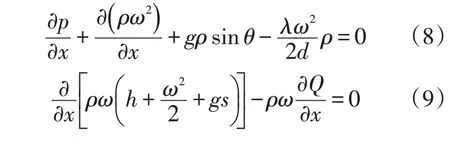
2 泄漏定位算法

通過現場傳感器采集到的起點溫度Ti、壓力pi和流量mi，依據Runge-Kutta法計算末點管道的溫度、壓力和流量，同樣通過采集到的末點溫度Tn、壓力pn和流量mn，反算起點管道的溫度、壓力和流量，得到圖1。

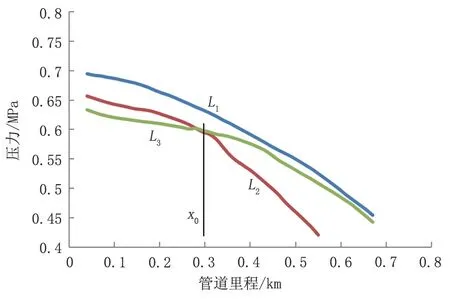
圖1 泄漏定位原理Fig.1 Leak location principle

假設在某一時刻t，由管道末點計算到管道起點的參數為Tnt、pnt、mnt，將判斷泄漏事故發生的壓力閾值定義為εt，則判斷泄漏的邊界條件為

當公式（10）成立，表示管內無泄漏點；當存在泄漏點時，管道內各點的相關參數會偏離計算結果，式（10）不再成立。當pnt＜pn時，管道內存在泄漏點。在管道的運行過程中，難免會出現關停壓縮機或停輸再啟動等工況，此時的監測數據會有較大波動，容易產生誤報，因此不考慮改變操作引起的擾動在時間內的報警，t1為泄漏點傳播到起點的時間，t2為泄漏點傳播到末點的時間，t3為擾動的熵變傳播到末點的時間，n為劃分管道的段數，Δt為報警閾值。

圖1 中L1代表未發生泄漏時的壓降，L2代表泄漏發生后從起點計算到末點的壓降，L3代表泄漏發生后從末點計算到起點的壓降。當發生泄漏時，泄漏點處氣體的密度和壓縮系數會發生變化，壓力也會發生瞬變。對于L2，泄漏點之前的仿真結果無限接近L1，泄漏點之后的仿真結果偏離L1，且距離x0越遠，偏離程度越嚴重；對于L3，泄漏點之后的仿真結果接近L1，泄漏點之前的仿真結果偏離L1，L2、L3的交點為x0即為泄漏點。泄漏定位流程圖見圖2。

3 實例計算

華北油田采油二廠從別古莊到霸一聯的輸氣管道全長2.7 km，管道規格為Φ213 mm×5.5 mm，管道輸量200 m3/min，實際運行壓力0.4～0.8 MPa，管輸介質成分CH4占98%，另外還有少量的C2H6、C3H8等。利用管線全面清管期間，在一些特定位置（充分考慮安全、環保的要求）人工制造幾處泄漏點，通過球閥控制泄漏過程。為了避免放氣時間與信號采集不同步，先進行閥門放氣，一段時間后關閉閥門，設置首站壓力0.65 MPa。圖3 和圖4 分別為泄漏點位于40.5 m時，發生泄漏后管道起點和末點的壓力隨時間變化的曲線。

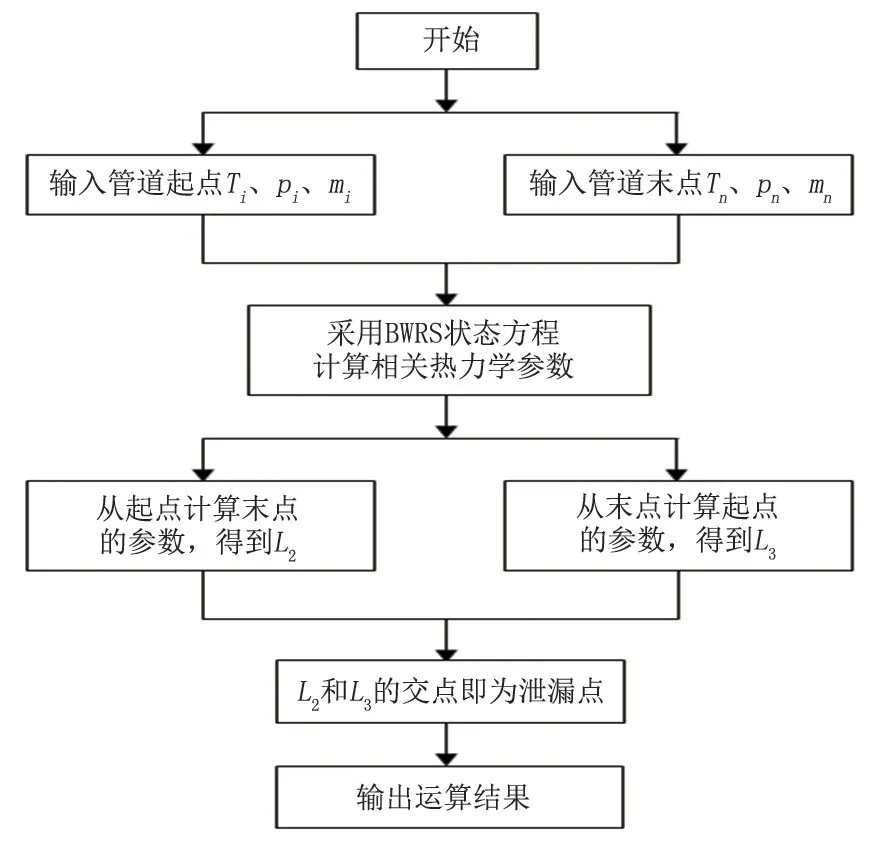
圖2 泄漏定位流程圖Fig.2 Flow chart of leak location

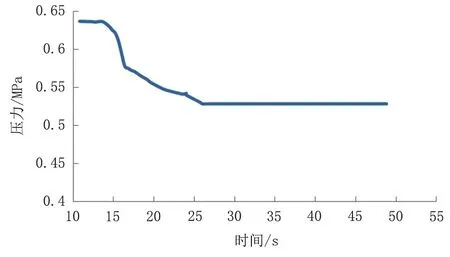
圖3 起點壓力隨時間變化曲線Fig.3 Change curve of start point pressure with time

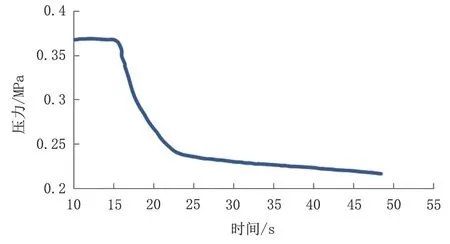
圖4 末點壓力隨時間變化曲線Fig.4 Change curve of final point pressure change with time

由圖3 和圖4 可知，在15 s 處管道發生泄漏，15～25 s 的時間段內首末點壓力急劇下降，而后趨于平穩，可見整個泄漏過程經歷了穩態—快瞬態—慢瞬態—穩態四個過程，流體從恒定流狀態向瞬變流狀態轉變，穩定之后的壓力值低于泄漏前的壓力值。為了更好地驗證改進后的Runge-Kutta 法對泄漏定位預測的準確性，控制閥門開度，以不同的泄漏率（即泄漏孔徑與管徑的比值）對模型進行驗證，同時與傳統的負壓超聲波定位精度進行對比，結果如表1所示。

表1 不同泄漏率下泄漏定位結果對比Tab.1 Comparison of leakage location results under different leakage rates

由表1可知，在泄漏位置一定的情況下，隨著泄漏孔徑和泄漏率的增加，Runge-Kutta 法和負壓波定位的定位誤差都在逐漸變小，通過結果對比，Runge-Kutta 法的定位誤差為0.4～2.5 m，小于傳統的負壓波定位誤差（5～12 m）。

地形地貌及管輸介質成分的不同決定了實際工況下的輸氣管道大多數為非等溫管道，為考察首末段溫差對定位精度的影響，在泄漏位置和泄漏率一定的前提下，通過提高首站和末站的溫度，在泄漏率5%的條件下用Runge-Kutta法和負壓波對泄漏進行定位，結果如表2所示。

由表2可知，隨著首末點溫差的不斷增加，兩種方法的定位誤差也隨之增大，但Runge-Kutta 法在定位精度上明顯優于負壓波定位，因此在溫差較大的情況下，Runge-Kutta 法可用于非等溫輸氣管道的泄漏檢測和定位。

管道輸量的大小對于不同泄漏孔徑也有一定影響。控制首站流量為150～300 m3/min，在泄漏率5%條件下，首站壓力設置為0.5～0.7 MPa，對326 m處的泄漏點進行定位，結果如表3所示。

表2 首末點溫差變化對定位精度的影響Tab.2 Influence of temperature difference between start and final point on positioning accuracy

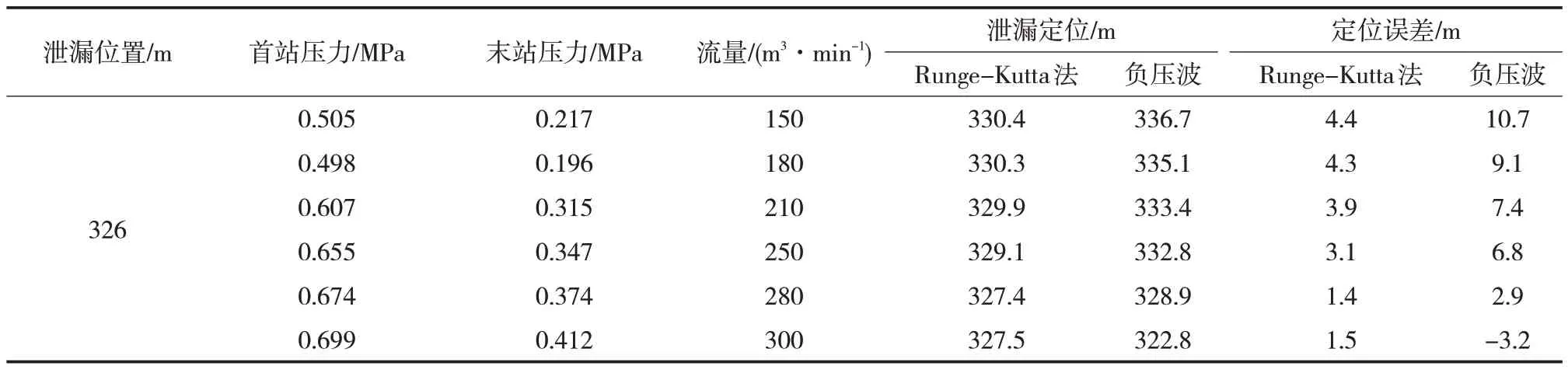
表3 不同管道輸量對定位精度的影響Tab.3 Influence of different pipeline volumes on positioning accuracy

由表3可知，隨著管道輸量的不斷增加，定位誤差整體減小。這是因為輸量越大，管道內的氣體流速越大，在泄漏孔處的流出速度越大，壓力波動越明顯。

綜上所述，對比不同情況下的定位誤差，對定位精度的影響因素排序由大至小是管道輸量、泄漏率、首末點溫差。

4 結束語

（1）通過采集到的首末點溫度、壓力和流量數據，應用改進后的Runge-Kutta 法可以計算管道各點的壓力分布，進而對泄漏點進行有效定位，該方法原理簡單，對現場操作人員的專業要求不高，易于實現，與傳統的負壓波相比具有一定的優越性。

（2）泄漏定位技術涉及多學科的融合和交叉，不應只注重現場傳感器的數據，隨著機器學習、數值分析的發展，今后應加強各學科之間的融合，提高定位精度。

（2）該方法只適用于干氣管道，對于含液較多的管道由于氣液流速不一致、氣液滑脫等現象并不適用，同時對于同一時刻有多處泄漏點的數據擾動考慮不足，今后應深入研究，加強模型的完善以提高定位精度。