正負偏差變量在數學規劃模型中的應用研究

摘? 要：數學建模是利用數學思想和方法解決實際問題的一種方式，線性規劃問題是數學建模的一項重要模型。本文從案例的實際出發，在探討線性規劃模型解決問題過程中，創造性地引入正負偏離變量，將約束條件加以放寬，并靈活應用序慣算法，使一個線性規劃的疑難問題得以圓滿的解決。

關鍵詞：線性規劃;正負偏離變量;序慣算法

中圖分類號：021? ? 文獻標識碼：A

一、問題的引出

線性規劃模型是數學建模的基本模型，在一定的條件下，對這一模型的優化，可使目標達到最優的決策，全國大學生競賽題許多與有優化有關，并用軟件加以解決。本文將從一個案例入手，利用數學模型探討問題最優解法。

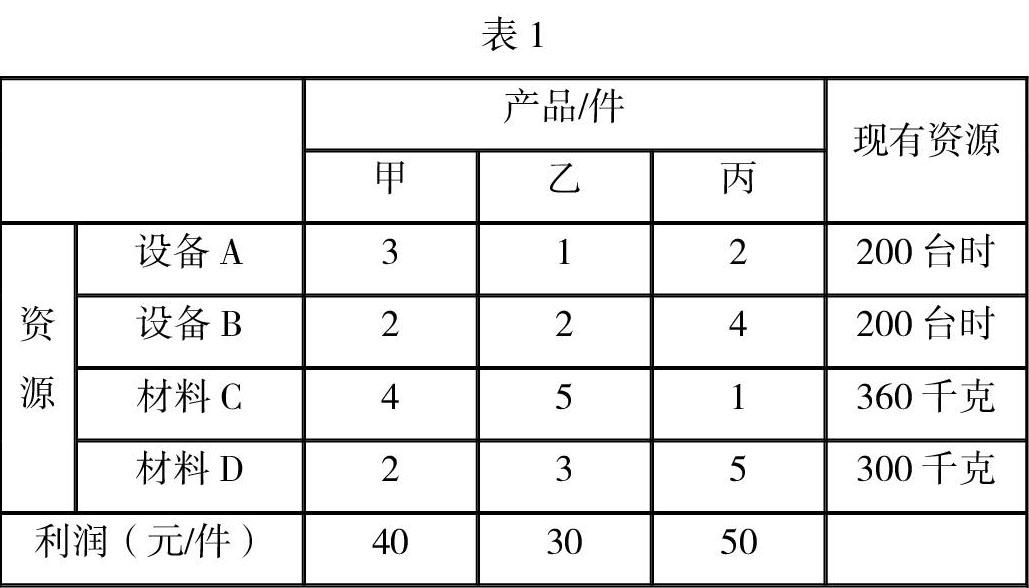
案例：某企業生產甲、乙、丙三種產品，這些產品分別需要在設備A、B上加工，需要消耗材料C、D，單件產品在不同設備上加工及所需要的資源如表一所示.已知在計劃期內設備的加工能力各為200臺時，可供應材料分別為360、300千克，每生產一件甲、乙、丙三種產品，企業可獲得利潤分別為40、30、50元.決策者根據企業的實際情況和市場需求，制定了幾個經營目標，這些目標的優先順序是：

（1）利潤不少于3200元.

（2）產品甲與產品乙的產量比例盡量不超過1.5.

（3）提高產品丙的產量使之達到30件.

（4）設備加工能力不足可以加班解決，能不加班最好不加班.

（5）受到資金的限制，只能使用現有材料，不能再購進.

假定市場需求無限制，企業應如何安排生產，使總利潤最大.

1、模型假設

假設表中的數據保持不變。

即：工藝不變;材料供應有保障;市場價格穩定。

2、建立模型

設： 分別為產品甲乙丙的產量（件）。

設備A的約束：

設備B的約束：

材料C的約束：

材料D的約束：

第一目標約束：

第二目標約束：

第三目標約束：

匯總為：

3、模型求解

使用lingo軟件編程，進行求解。結果表明是無解。因此，線性規劃模型利用傳統的方法，無法尋求最優解。作為問題本身應該有優化解。

二、模型的分析與改進

考慮到案例中5個目標順序中的前4個目標可考慮放松，第5個目標明確規定不能改變。

因此可將目標放寬為：

（1）利潤為3200元左右;

（2）產品甲與產品乙的產量比例在1.5左右;

（3）提高產品丙的產量使之達到30件左右;

（4）設備加工能力不足可以加班解決，設備A和B可以考慮加班在200臺時左右，但加班數最小。

為了解決這一問題，我們考慮引進正負偏差變量來進行處理：

假定

是兩個偏差變量，且滿足以下條件：

體現在模型中，就是將（2）、（3）、（6）、（7）（8）可以考慮放寬條件，結合題意，考慮引進目標函數，得到以下修改模型：

這樣，原來的線性規劃模型就轉化成目標規劃模型了。

三、使用序慣算法。

在處理正負偏差變量過程中，考慮到指數位置的正負號在lingo程序中不易表達，我們不妨規定：分別用s1，s2替代

具體來說，就是用s11，s12，s21，s22，s31，s32，s41，s42，s51，s52替代

因此，在lingo軟件中，編程得到以下程序：

在運行這個程序時，把前面4個目標函數

按次序與約束函數逐一運行計算，得出結果代入下一程序進入計算，最終計算出所需結果，該運算法，稱之為程序的序慣算法。具體過程操作如下：

運行lingo程序得到的結果如下：

結果顯示s11=0，將其代入下一步程序中，在軟件lingo中運行第二目標程序。

結果顯示，s11=0，s22=0，將結果代入程序，再在linguo程序中運行第三目標程序命令。結果顯示，s11=0，s22=0，s31=0，s32=0.將此結果代入程序，運行最后一個目標程序。

其顯示的結果，用數學式表達如下：

四、模型的檢驗

將這些結果導入修改后模型中，

發現：設備B加班16臺時，其余目標全部滿足，其利潤達到3220元，比我們原先計劃3200元還多20元，這個結果正是我們所希望的！

五、結束語

利用lingo解決線性規劃和非線性規劃問題，是比較方便的方法。但是如果出現無解的情況，就需要考慮將約束條件進行適當的放寬。也就是在原條件得基礎上引進正負偏差因素，并將正負偏差控制在最小的范圍內，以便使約束條件不至于偏離原條件太遠。在此過程中，必然需要引進目標規劃函數，從而在新的條件下達到最優解。

參考文獻

[1]? 韓中庚.實用運籌學[M].北京：清華大學出版社.2007.

[2]? 朱素玲李文婷劉秀英.變量選擇偏離對預測的影響研究[J].決策與統計.2016.6.

[3]? 田森.基于運籌學運輸問題模型的電煤采購決策[J].工業技術創新.2017.1.

[4]? 黃青群.淺談最優化方法在數學建模中的應用[J].高教學刊.2016.11.

[5]? 耿德志.線性規劃求解算法研究[J].軟件導刊.2011.6

作者簡介：熊慶如（1964—），男，江西宜豐人，浙江東方職業技術學院教師，碩士學位，副教授。研究方向：數學教育。

基金項目：本文為浙江東方職業技術學院2018—2019年度院級課題：“雙創”背景下高職產業學院的組織機制與培養模式的研究”（DF2018YB15）研究成果