基于不確定度分析的計算結果有效數字確定方法

張馨睿，吳颯，陳仁軍，周學亮

（1.北京航空航天大學，北京 100083； 2.陸軍裝備部航空軍事代表局，上海 200233；3.蘇州天航長鷹科技發展有限公司，蘇州 215155）

背景

在科學研究與工程實踐中，不可避免地要進行大量的數據計算，也就是把一些數值作為已知量，通過規定的計算方法以數值的方式給出運算結果。無論是作為已知量還是作為運算結果的數值都是通過有效數字的方式給出，也就是說這些數值在本質上具有一定的不確定性。數據計算不僅應當按照計算方法給出理論結果，也應當把來自于數據源和計算方法的不確定度信息正確地傳遞給計算結果的使用者，一般是以有效數字位的方式完成數據結果和不確定度信息的傳遞。因此，如何確定計算結果的有效位數是十分必要的，不正確的有效數字位會造成計算結果中所傳遞的不確定度被錯誤地使用。正是因為有效數字位與不確定度存在著本質上的關聯，因而有必要通過不確定度分析的方法進行有效數字位的確定。

1 概念

1.1 有效數字的含義

數據的來源一般有兩種途徑，一種是通過直接測量得到的測量量，另一種是通過計算的得到的計算結果。對于第一種情況，有效數字是反映被測量大小的全部數字，包含準確數字以及一位帶有不確定度的估讀數字。有效數字的最末一位是估讀的，因此只有最末一位數字具有不確定度，有效數字的不確定度代表了估讀數字的不確定度，可以通過有效數字的不確定度大小來確定哪位數字是估讀數字。有效數字也在一定程度上表達了測量結果的不確定度[2]，其最末數字位數離小數點越近，被測值的不確定度越大。對于第二種情況，通過對計算結果的修約得到其有效數字。無論是直接測量值還是通過間接計算得到的數值，當以有效數字表示時，都要遵循只有最末位是估計值，其他位都是準確數字的要求。只有這樣才能保證正確反映出分析量的多少，才能使結果被正確使用。

1.2 不確定度的含義

不確定度的概念首先應用在測量結果的表述中，用以合理表示被測值分散程度。無論是直接測量量還是通過計算得到的測量值，其結果的完整表示應該是被測量量加上相應的不確定度。不確定度反映了測量的質量，不確定度小，表明測量結果距真值的偏離范圍就越小，質量就越高，其使用價值就越高，相反，不確定度越大，則偏離范圍就越大，質量就越低，其使用價值就越低。

2 測量不確定度評定

進行測量不確定度評定時，比較常用的方法是應用測量不確定度傳播率的方法（GUM法），具體過程包括建模、標準不確定度評定、計算合成標準不確定度和計算擴展不確定度。

2.1 建模

被測量的值的不確定度取決于參與計算的其他分量，確定這種取決關系即為建模。被測量Y的最佳值y由X1，X2，…，XN的最佳值x1，x2，…，xn得到，即y=f(x1，x2，…，xn)。y的標準不確定度 u(y)取決于 x1，x2，…，xn的標準不確定度。

2.2 標準不確定度評定

A類評定方法是為了得到測量數據的標準差的最佳估計值，通過一系列測量數據使用統計方法進行評定。通常使用方法有貝塞爾法、最大殘差法、極差法、最小二乘法。

B類評定方法是通過非統計方法進行的，B類評定方法中最常見的是使用來自于技術資料、證書或手冊中提供的數據。這些數據往往提供了可能的取值范圍，但其概率分布要進行假設，根據已知信息可假設為正態分布、均勻分布、反正弦分布、雙均勻分布、三角分布，如果信息缺乏，一般情況下可以假設為均勻分布。

2.3 合成不確定度計算

合成不確定度是在不確定度傳播公式下，自變量的標準不確定度經函數關系傳播到因變量所產生的不確定度。不確定度傳播公式為：

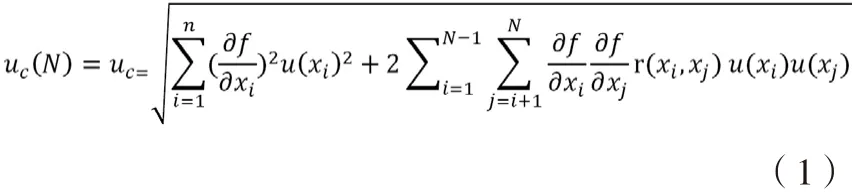
假設自變量之間互不相關，則r(xi，xj) =0合成不確定度公式為：

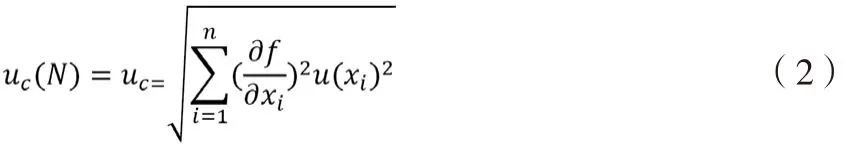
2.4 擴展不確定度計算

擴展不確定度表示測量值大部分合理地包含在此區間內，擴展不確定度由合成不確定度與包含因子相乘求得：

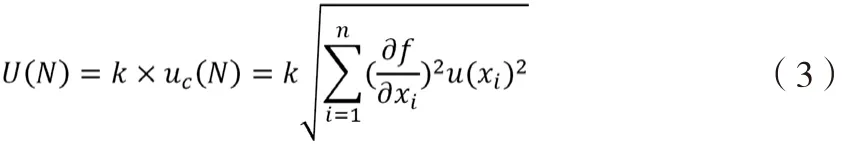
包含因子常用求取方法如下[3]：

1）當參與運算分量的自由度已知時，根據下式（4）計算合成不確定度的有效自由度

vi—u(xi)的自由度。

由t分布求出包含因子P為置信水平，可取0.95，0.99，0.997，可根據t分布表，通過p與v查表得tp(v)，即k。

2）當參與運算分量的自由度未知時，可通過賦值法求取k。

實際測量工作中，大多數測量量的分布可以近似為正態分布，對于正態分布的情況，包含因子取決于期望的置信概率。在工程上一般的置信概率取值為90 %、95 %、99 %，對應的包含因子分別為2、2.56、3。其他分布情況，也有類似的幅值方法，具體可以參閱測量不確定度評定和數理統計相關書籍。

3 計算結果的不確定度

計算結果的不確定度評定與測量的不確定度評定非常類似。

3.1 建模

計算結果的來源公式即為模型。

3.2 標準不確定度評定

計算所面臨的情況不存在一系列測量數據，不使用統計方法進行評定，因此不使用A類評定方法。

計算過程的不確定度應使用B類評定方法進行評定，數據可來源于資料或前期計算結果，因此在進行標準不確定度評估時，參與計算的每個數值都是不確定度評定時的來源。如果數值給出了不確定度信息，則可以利用該信息計算其標準不確定度。如果該數值僅以有效數字給出，由于沒有給出其他信息，故假設其為均勻分布，根據修約規則，其量值變化半寬度為a，標準不確定度等于

3.3 合成標準不確定度計算

計算結果的合成標準不確定度計算與測量不確定度計算類似。

合成標準不確定度是在不確定度傳播公式下，參與計算分量的標準不確定度經靈敏度系數傳播到計算結果所產生的不確定度。不確定度傳播公式為：

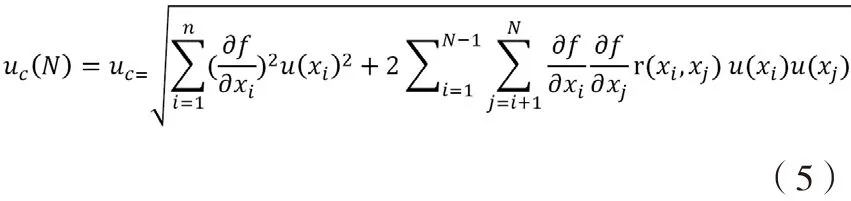
假設參與計算的分量之間互不相關，則r(xi，xj) =0，合成標準不確定度公式為：

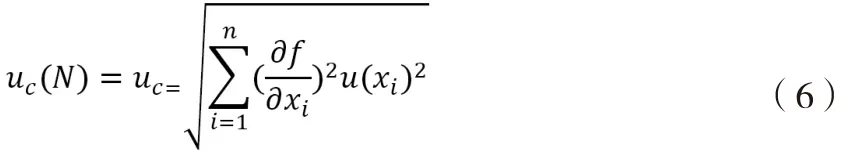
3.4 擴展不確定度計算

計算結果的合成標準不確定度計算與測量不確定度計算類似，擴展不確定度由合成不確定度與包含因子相乘求得：

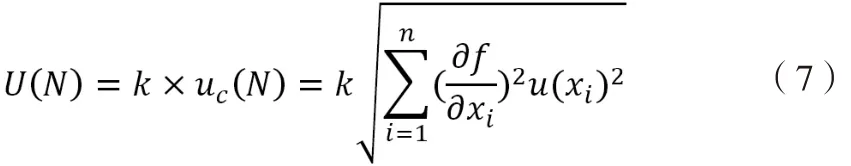
k通過賦值法求得，取決于預期的置信概率，在工程上一般的置信概率取值為90 %、95 %、99 %，對應的包含因子分別為2、2.56、3。

4 計算結果的有效數字確定

4.1 常規方法

數值計算是科研工作的核心，計算公式可以是常規的算術計算，也可以是非常復雜的計算方法。下面就幾種常見的計算方法，給出目前采用的有效數字確定原則[1]。

加減法：最終結果的有效數字的末位與參與運算變量中有效數字末位最高位者相同。

乘除法：最終結果的有效數字的位數與參與運算變量中有效數字位數最少者相同。

乘方運算：最終結果的有效數字位數與底數有效位數相同。

對數運算：最終結果的有效數字位數與真數的有效位數相同。

4.2 基于不確定度分析的方法

有效數字的不確定度與最末一位修約數字有直接聯系，無論是直接測量還是間接計算得到的結果，其不確定度都表現了計算結果在哪個數位上是不確定的，確定有效數字位數即確定修約數字在哪位，可以通過計算結果的大小與其不確定度來確定。進行最終結果報告時，結果的末位應與不確定度的末位保持一致（如GJB 3756）。在進行計算時，根據修約規則，有效數字中只包含一位不確定數字就是最末一位修約數字，因而對于不確定度的關注只有一位數字即首位數字。根據預期的置信概率對應的包含因子，得到擴展不確定度，然后根據通用的修約規則，得到只有一個數字位的數值，如該位數值大于等于5，則有效數字位進一位，否則有效數字位保持不變。例如0.04對應的有效數字位是小數點后第二位，0.05對應的有效數字位是小數點后1位[5]。

4.3 在常用計算方法中的應用

1）加法：N=f(x1，x2，…xn)=x1±x2±…±xn

合成不確定度：

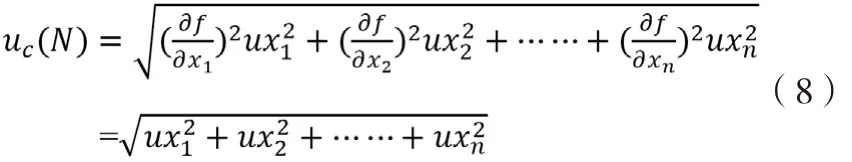
這是最簡單的計算過程，當只有一個數值具有最少有效數字時，它將占主導地位，其他數值的影響可以忽略。通過公式就可以明顯看出。這種情況下與常規方法是一致的。

只有當存在多個數值具有相同的最小有效數字時，才需要根據不確定度傳播公式計算其合成標準不確定度。

2）乘法：N= f(x1，x2，…xn)=x1×x2×…×xn

合成不確定度：

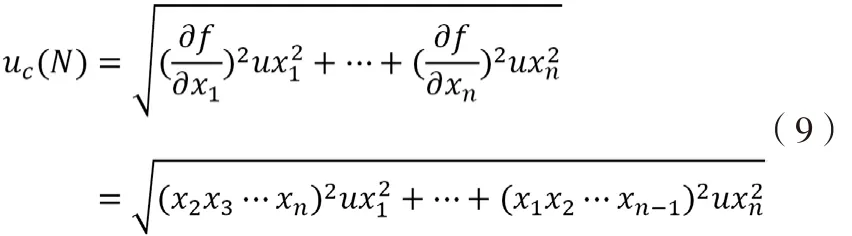
3）除法：N= f(x1，x2，…xn)=x1÷x2÷…÷xn

合成不確定度：

4）乘方（以平方運算為例）：N=f(x)=x2

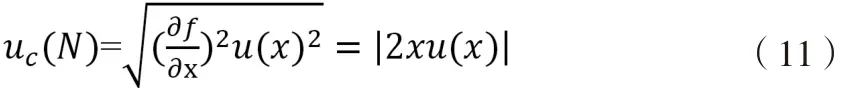
合成不確定度：

6）對數:N=f(x)=logax

合成不確定度：

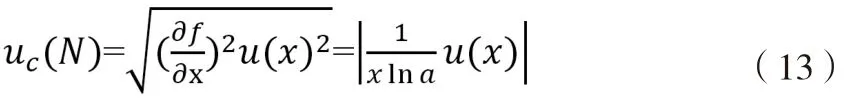
7）指數:N=f(x)=ax

合成不確定度：

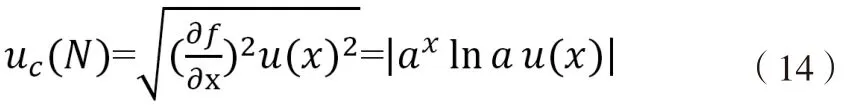
5 示例與分析

5.1 加減法運算

在加減法運算中，如若參與運算的分量中最小有效數值只有一個時，其產生的不確定度占主導地位，其他數值產生的不確定度可以忽略，因此這種情況下，常用的確定方法與本文提出的確定方法得出的結果相同。

例 1：N=x1+x2+x3+x4+x5+x6，x1=1.325，x2=1.364，x3=1.102，x4=1.32，x5=1.364，x6=1.182，計算結果N=7.657。

1）使用本文提出的確定方法：

x1、x2、x3、x4、x5、x6服從均勻分布，其標準不確定度為

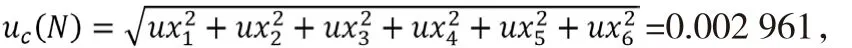
由于只有一個數據占主導，且假設其為均勻分布，因而認為計算結果也基本服從均勻分布，其擴展不確定度為，0.002 961×2≈0.006故有效位進一位即0.01，按照修約規則N的最終表示結果是N=7.66。

2）使用常用確定方法：

參與運算的有效數字中小數位數最少者為2，因此最終計算結果中保留的小數數位也是2位，最終計算結果為7.66。兩種方法給出了同樣的結果，原因是在加減法運算中，靈敏度系數是常數1，只有一個數據具有最小的有效位，在本文提出的方法中不確定度取決于最小有效位；常規方法中也取決于最小有效位。

例 2：N=x1+x2+x3+…+x100，x1=x2=x100=0.013 25，N=1.325

1）使用本文提出的方法：

x1、x2、…、x100服從均勻分布，其標準不確定度為

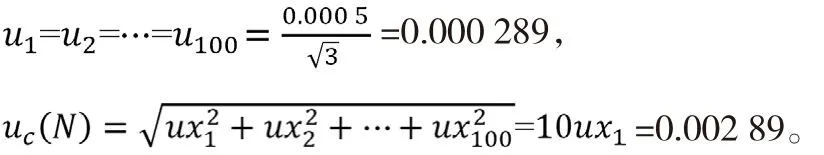
由于每個數據的不確定度都相同，且假設其為均勻分布，因而認為計算結果也基本服從均勻分布，其擴展不確定度為0.002 89×2≈0.005，故有效位即0.01，按照修約規則N的最終表示結果是N=1.33。

2）使用常用確定方法：

參與運算的最小有效數位為4，因此運算結果的有效數位也是4位，最終計算結果為1.325。

當參與加減法運算的變量修約數字所在位數相同且變量個數增加到一定程度時，采用兩種方法得到的結果是不同的，原因是由于變量個數的增加使得擴展不確定度擴大了十倍，有效位也隨之發生改變，此時常用的方法仍根據變量中小數位最小者確定有效位是不合理的。

5.2 乘法運算

V=a×b×h，a=5.375，b=4.230，h=4.110， 結 果 為V=93.445 987 5。修約截尾產生的不確定度屬于均勻分布，標準不確定度

按正態分布95 %置信概率的包含因子為2，則擴展不確定度為0.02，確定有效位是與不確定度首位，最終表示結果是V=93.45。而采用常規方法，最終表示結果的有效位是所有數據中最小有效位數，表示結果是V=93.446。

采用兩種方法得到的結果是不同的，原因在于采用常規方法時將不確定度傳播中的靈敏度系數全部看作常數1，采用本文提出的方法，在進行不確定度傳播計算時，真實的考慮了靈敏度系數，參與運算變量的靈敏度系數大于常數1，因此得到的結果會偏大。

5.3 除法運算

5.4 平方運算

E=v2，v=6.23，計算結果 E=38.812 9。則。按正態分布95 %置信概率的包含因子為2，則擴展不確定度為0.035 972×2≈0.1，確定有效位是與不確定度首位，最終表示結果是v=38.8。而采用常規方法，最終表示結果的有效位是底數有效位數，表示結果是v=38.8。

5.5 開方運算

5.6 對數運算

y=log10x，x=20.11計算結果y=1.303 412，標準不確定度，則0.000 062 3，按正態分布95 %置信概率的包含因子為2，則擴展不確定度為0.000 062 3×2≈0.000 1，確定有效位是與不確定度首位，最終表示結果是y=1.303 4。而采用常規方法，最終表示結果的有效位數與真數的有效位數相同，表示結果是y=1.303。

6 結論

本文基于不確定度傳播原理對確定計算結果有效數字的方法，計算由自變量修約截尾產生的標準不確定度傳播到測量值的合成不確定度，計算結果有效數字的確定與擴展不確定度相關，計算結果的有效位與擴展不確定度的首位相同。采用常用方法與本文提出的方法得出的結果是有差異的，原因在于常規的方法由于沒有考慮計算中各數據對不確定度的貢獻是與計算方法中該變量的偏導數有關的，因而會造成一定的偏差，本文提出的方法考慮了在不確定度傳播過程中靈敏度系數的影響，根據不確定度更準確地確定了有效位，文中舉例說明兩種確定法則的差異。使用本文提出的方法進行有效位的確定仍然會造成不確定度的失真，因此在最終計算結果的表示形式上以有效位加不確定度共同表示較為合理。