自動化立體倉庫中出入庫任務順序與出庫位置選擇集成優化研究
韓東亞,陳 然,余玉剛,郭曉龍
(中國科學技術大學管理學院,安徽 合肥 230026)
1 引言
近年來,隨著電子商務的高速發展,以阿里、京東和蘇寧為首的電商企業迅猛崛起,我國的自動倉儲系統市場呈現穩步高速增長態勢,傳統的批量化、單一化產品越來越難以滿足消費者的需求。電商物流呈現出訂單數目大、海量SKU、訂單時效性高、隨季節波動性大的特點。傳統的自動化立體倉庫需要先使用堆垛機取出整托盤貨物,然后將整托盤通過傳送帶送至分揀系統。取貨人員按照訂單從整托盤中取出所需數量的貨物,并將托盤放回至傳送帶使其入庫。托盤在傳送帶往往花費大量的等待時間,分揀作業效率低下,無法滿足電商物流中多品種、小批量的消費需求。
多出庫位置的自動化立體倉庫(Automated Storage and Retrieval System with Multiple In-the-Aisle Pick Positions, 簡稱ASRS-MIAPP)是一種新型的倉庫技術,能有效地改善上述分揀作業效率低下的問題。與傳統的單出入口自動化倉庫不同,ASRS-MIAPP在貨架底層有多個出庫位置,可被視為單入口多出口的倉庫系統。ASRS-MIAPP中有兩種類型的過道:揀選過道和堆垛機過道。其中揀選過道比堆垛機過道略寬,為取貨人員提供移動空間進行貨物揀選。ASRS-MIAPP能夠有效地將存儲和分揀作業集成在一起,既減少了占地面積,提高了空間利用率,減少能量損耗,同時又能減少工人數量,降低人力成本。目前已得到眾多國際知名公司,如Publix Super Markets, Wal-Mart, Walkers, Ferrero GmbH等的廣泛使用[1]。
在ASRS-MIAPP中,出入庫任務的合理調度,對整個系統整體運作起著至關重要的作用。當出入庫任務的完成順序選擇較差時,堆垛機運作的距離會變大,既延誤了完成下一批任務的時間,也延誤了出庫貨物到達顧客的時間,對企業造成不好的影響。同時,出口貨物釋放到出口的位置,也會影響到堆垛機完成兩個連續任務的運作距離。因此,出入庫任務的調度和出庫位置的選擇,是緊密相連的聯合決策問題。然而,隨著問題規模的擴大,求解難度急劇上升,如何快速求得最優解或近似最優解至關重要。
目前,針對自動化立體倉庫系統運作績效問題,國內外有很多學者進行了研究。Roodbergen和Vis[2],Gagliardi等[3],Boysen和Stephan[4]從不同的角度對現有研究進行了綜述分析。Roodbergen和Vis[2]提出可以通過四種控制決策包括存儲策略、批處理、堆垛機停頓點策略和出入庫調度策略等來有效地提高自動化立體倉庫的績效。Han等[5]指出,自動化立體倉庫存取順序問題類似于旅行商問題。對于動態環境下的存取順序問題,可以通過兩種方法來解決:塊調度和動態調度。塊調度是指選擇一個塊,對其中的所有出入庫任務進行調度,當此塊內的所有作業全部完成后,再進行下一個塊調度;而動態調度則是指每次有新的任務加入時對所有任務重新排序,采用截止日期優先的方式,確保不會過度延遲出庫任務。Lee和Schaefer[6]研究了一種特殊情況,即系統中的任意空位均可作為存貨位置使用,作者首先求解一個線性指派模型,然后使用排序算法求解,此算法在空位數量較小時可以找到系統最優解。在Lee和Schaefer[7]的另一項研究中,根據先來先服務(FCFS)規則操作入庫任務,而通過指派問題的算法優化出庫任務順序。Chen等[8]在考慮每個單元負載的停留持續時間的情形下建立混合整數模型,并構造啟發式以及禁忌搜索算法解決此問題。Eynan和Rosenblatt[9]提出最近鄰域搜索算法并應用于分類存儲策略中。Gharehgozli等[10]針對具有兩個進出口的自動化立體倉庫提出了一種多項式時間的算法解決出入庫調度問題。
以上研究均假設堆垛機每次只能存取一個負載單元,與之相反,雙梭立體倉庫可以一次存(或取)兩個負載單元,因此,出入庫任務的組合更多更復雜。Keserla和Peters[11]用基于最小周長的優先規則方法解決雙梭立體倉庫調度問題。Sarker等[12,13]針對類似的問題提出了基于最近鄰的簡單啟發式方法。Yang Peng等[14]則研究多梭立體倉庫調度問題,建立了混合整數模型并用可變鄰域搜索方法求解。對于類似的問題,一個兩階段禁忌搜索方法和遺傳算法結合修改最近鄰啟發法分別在文獻[15]和[16]中給出。目前很少有學者針對ASRS-MIAPP系統進行研究,Ramtin和Pazour[17]在隨機存儲策略下,建立了堆垛機行走時間模型,分析不同系統尺寸,不同系統構造(單層多出庫位置和雙層多出庫位置)對系統績效的影響。Ramtin和Pazour[1]考慮了不同需求曲線下貨物的存儲問題,在假設有無限多的出庫位置下,他們建立了連續的數學模型,并與離散事件仿真的結果作對比,發現只有0.1%的差距,驗證了此連續模型的有效性。
國內學者也對自動化立體倉庫的運作績效進行了深入的研究。田國會等[18]考慮自動化立體倉庫固定貨架系統中出入庫策略優化問題,提出了一種新的自適應啟發式方法,使用最近點搜索算法獲得初始種群的解,然后進行逐步迭代,結果表明算法能在較短的時間里獲得很好的解。王雯等[19]提出一種基于層次分析法和遺傳算法相結合的出入庫調度優化算法,并使用仿真的方式驗證了算法的有效性。劉韜等[20]采用面向對象的賦時Petri網研究了出入庫調度問題,建立了數學模型,并分析了該模型的死鎖問題。鄧愛民等[21]以醫藥倉庫為例,建立了基于時間的多目標貨位優化模型,并使用遺傳算法求解模型。李鵬飛和馬航[22]以出入庫效率和貨架穩定性作為優化目標建立數學模型,采取病毒協同遺傳算法進行仿真對比,結果顯示此算法能夠獲得較好的解。靳萌等[23]針對軍用維修器材倉庫,提出了考慮物資周轉率和相關性的貨位優化模型,并設計了一套基于Pareto保持和模擬退火的算法,驗證了此模型的有效性。劉臣奇等[24]構建了貨物揀選路徑問題的優化模型,提出了改進的蟻群算法,結果顯示該算法相較于基本蟻群算法收斂速度顯著提高,具有很好的可行性。常發亮等[25]考慮了周轉貨箱的容量限制,根據自動化倉庫貨物揀選的特點建立了數學模型,用遺傳算法對該模型進行求解,數值結果表明此算法高效可靠。
本文與以上學者研究的區別在于(1)本文研究一個單入口、多出口的自動化立體倉庫,因此即需要考慮出入庫任務的操作順序,也要考慮出庫任務被分配到哪一個出庫位置的問題。而以上學者主要研究單入口單出口的倉儲系統,只需要考慮出入庫任務的操作順序既可。(2)目前研究此系統的文獻聚焦于系統績效,以及貨物存儲策略方面的研究,本文首次研究此系統出入度調度策略問題。
2 出入庫調度與出庫位置選擇集成優化模型
2.1 問題描述
本文的問題可以描述為:在一個多出口位置的自動化立體倉庫(如圖1所示)中,有一系列貨物等待存儲,同時還有一系列貨物等待取出。堆垛機既可以每次只完成一個入(或出)庫任務,也可以每次先完成入庫任務,再完成出庫任務。
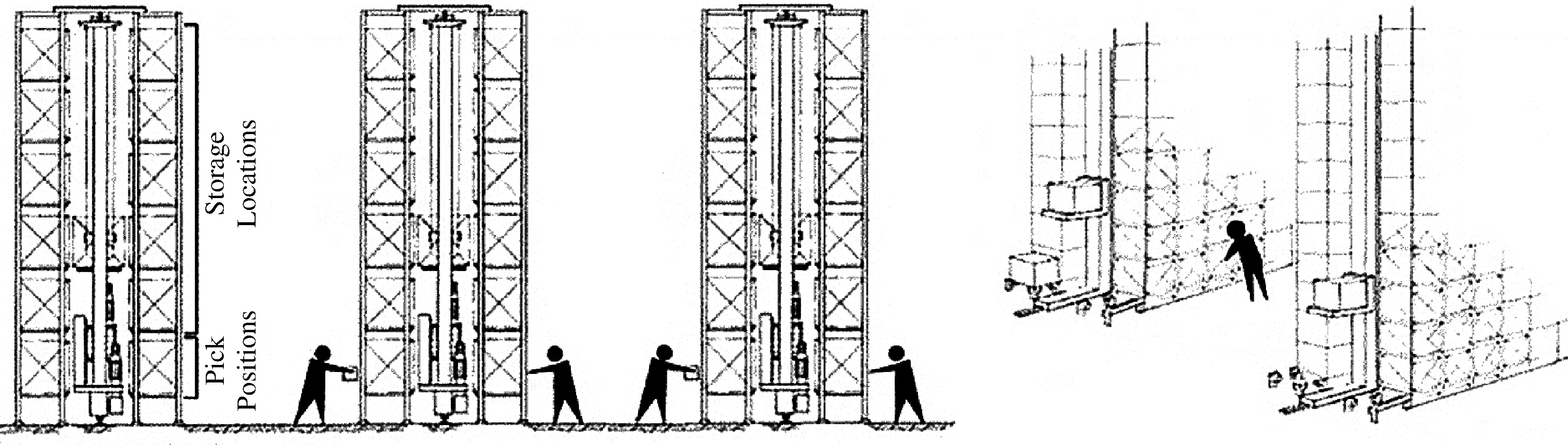
圖1 ASRS-MIAPP示意圖,左圖為左視圖,右圖為側視圖(引自Ramtin和Pazour[1])
上述堆垛機操作過程中存在以下特點:
(1)入庫任務順序約束:一般來說,需要存放的貨物會在傳送帶上等待堆垛機完成入庫任務。由于很難在傳送帶上改變待存放貨物的位置,因此入庫任務按照先到先服務的模式進行。
(2)多種出入庫路徑情形:我們考慮堆垛機的停頓點策略為停留策略,即堆垛機會在完成出庫(或入庫)任務的位置處停留,等待下一個任務。當完成的任務為入庫任務時,堆垛機會停留在完成上架的標準化托盤所在的位置上;當完成的任務為出庫任務時,堆垛機會停留在完成出庫的標準化托盤所在的出庫位置處。因此,堆垛機啟動的位置取決于前一個任務。另一方面,堆垛機的作業模式有以下三種:(1)單一入庫任務:堆垛機從完成上一個任務的停頓點處空載到入口,將從入口處將要存放的標準化托盤運送到給定存儲位置上。(2)單一出庫任務:堆垛機從完成上一個任務的停頓點處空載到所需托盤所在位置,從貨架上取下并將它運送到某個揀貨位置處。(3)復合作業:堆垛機從完成上一個任務的停頓點處空載到入口,將要存放的標準化托盤運送到給定存儲位置上,空載到需要取出的托盤所在位置,從貨架上取下并將它運送到某個揀貨位置處。考慮到停頓點和堆垛機作業模式之間的組合,堆垛機會根據出入庫任務順序和出庫位置選擇按照相應的路徑移動。如圖2所示,堆垛機一共有6種可能的路徑移動:(a) 停頓點在貨架上的單一入庫任務;(b) 停頓點在貨架上的單一出庫任務;(c) 停頓點在貨架上的復合作業;(d) 停頓點在出庫位置處的單一入庫任務;(e) 停頓點在出庫位置處的單一出庫任務;(f) 停頓點在出庫位置處的復合作業。

空心圓代表停頓點;實心圓代表出庫位置;實心方塊代表入庫位置;實線代表堆垛機負載移動路線;虛線代表空載移動路線圖2 堆垛機可能的移動情形
本文考慮如何進行出入庫任務的調度并確定出庫任務釋放到哪一個出庫位置,使得堆垛機完成所有任務的總距離最短。該問題的決策包括出入庫任務的完成順序,以及出庫位置的選擇。為了方便問題表述和模型建立,我們假設上述倉儲系統:
(1)堆垛機既可以進行單一作業,也可以進行復合作業,其運作能力為每次一個標準化托盤;
(2)堆垛機可以沿水平方向和豎直方向同時運動,且速度為常數;
(3)堆垛機的停頓點策略為停留策略,即堆垛機會在完成出庫(或入庫)任務的位置處停留,等待下一個任務;
(4)系統采用專用存儲策略。因此,對于要存放的標準化托盤,其存儲位置已知。
2.2 模型構建
考慮有m個入庫任務,n-m個出庫任務,以及K個出口位置。不失一般性,對任務進行編號,i=1,2,…,m表示入庫任務,j=m+1,…,n表示出庫任務,另定義任務0和T為虛擬任務,分別表示開始和結束任務;令Si為對應入庫任務i的位置,Rj為對應出庫任務j的位置,Ok為出口位置k,I和E分別為對應虛擬任務0和T的位置。

定義lk為出庫位置k=1,2,…,K到入口的距離;dijkp為堆垛機從完成任務i后所停留的位置k,移動到完成任務j后所停留的位置p的距離,其中d0jIk表示堆垛機從入口I移動到完成第一個任務所在停留點位置k的距離,diTkE表示堆垛機從完成最后一個任務i所停留位置k,移動到虛擬任務T所在停留點位置E的距離,具體計算公式見表1。其中四元數組(A,B,C,D)定義為堆垛機從任務A移動到任務B,任務A和B的停頓點分別為C和D;堆垛機按照切比雪夫距離移動;此外(xi,yi),(lk,0)分別是任務i和出庫位置k的笛卡爾坐標。

表1 不同情況下對應的邊權重計算公式
決策變量定義為:當堆垛機完成任務i后立即完成任務j,同時任務i的停頓點為k,任務j的停頓點為p時,Xijkp=1,否則為0。其中X0jIp,XiTkE取1時,分別表示第一個任務為j,且停頓點為p和最后一個任務是i,且停頓點是k;任務i完成的次序ui。于是,多出口位置的自動化立體倉庫出入庫調度與出庫位置選擇集成優化模型可以表示為:
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
u1=1,
(9)
2≤ui≤n,?i≠1,
(10)
(11)
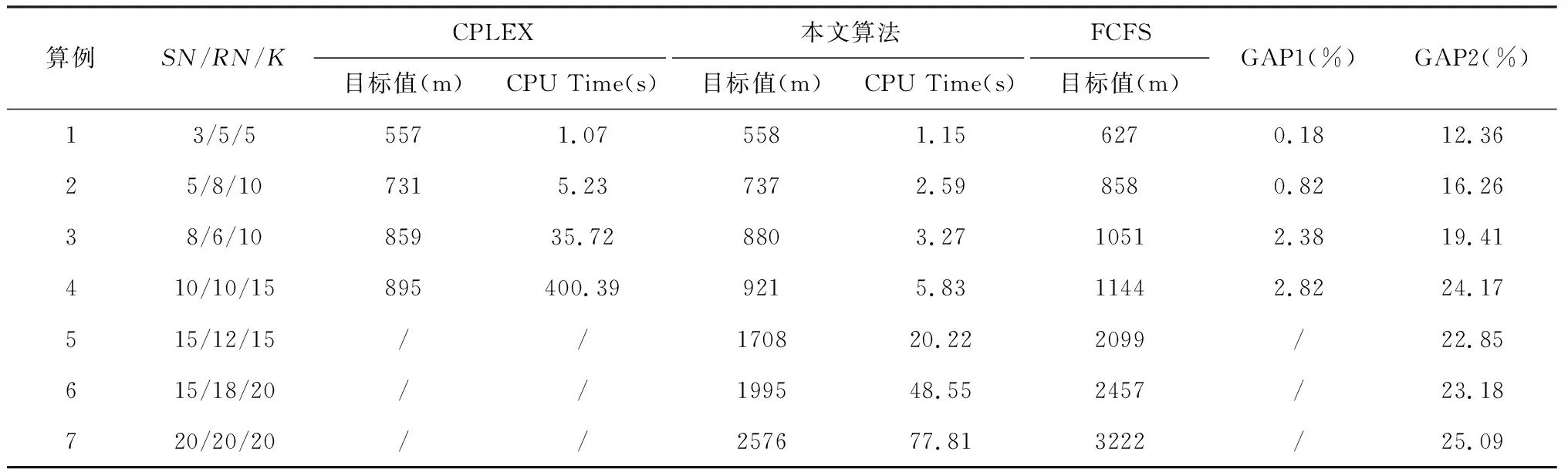
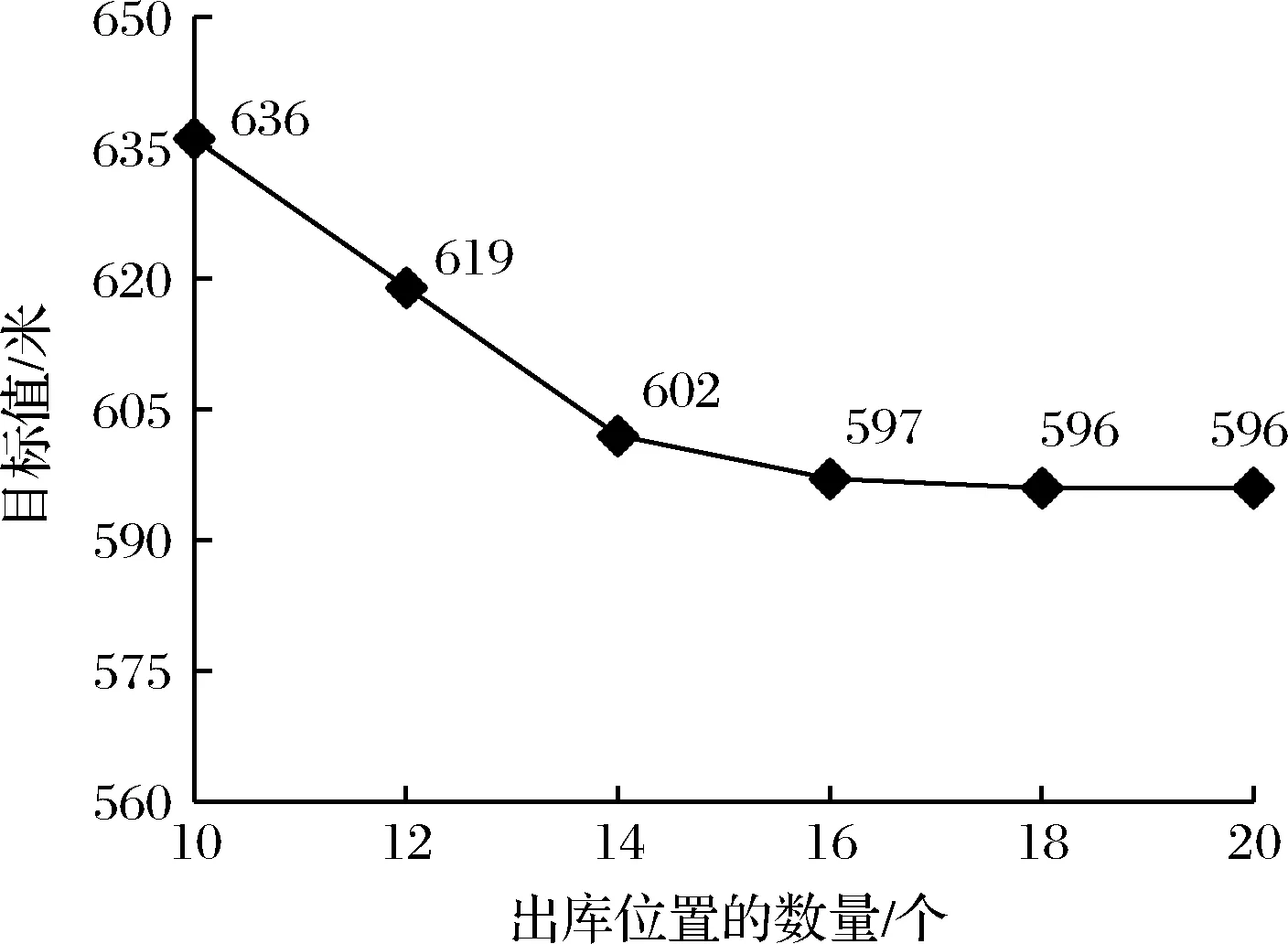
ur (12) Xijkp={0,1},?i,j∈J,?k,p∈L. (13) 目標函數(1)表示最小化堆垛機完成所有任務的移動距離;約束(2)和(3)確保堆垛機有起始任務和終止任務;約束(4)和(5)表示每個任務的前后均有任務;約束(6)和(7)表示堆垛機在每個停頓位置最多停頓一次;約束(8)表示每個任務對應的停頓點唯一;約束(9)、(10)和(11)表示避免產生子回路;約束(12)表示入庫任務按照次序完成;約束(13)給出決策變量的取值范圍。 本節分析模型的復雜性,證明此類問題是NP-hard問題。 定理1出入庫調度與出庫位置選擇集成問題是NP-hard問題。 證明:本文將該問題的一類特殊情況轉化為TSP旅行商問題。構造研究問題的實例如下:設有m個出庫任務,m個出庫位置。我們設置一個虛擬點AP代表堆垛機的初始點和終止點,并假設虛擬點AP到出庫任務所在位置和出庫位置的距離均為0。為了防止堆垛機從任務所在位置(或出庫位置)直接移動到另一個任務所在位置(或出庫位置),設任意兩個任務所在位置(或出庫位置)之間的距離足夠大。原問題轉化為求解從AP點出發,訪問每一個任務位置和出庫位置并回到AP點的最短回路。因此,求解此類特殊問題等同于求解TSP旅行商問題,由于TSP是NP-hard問題[26],原問題也是NP-hard問題。 本文研究的堆垛機出入庫調度與出庫位置選擇集成問題屬于NP-hard問題,隨著問題規模的擴大,無法在有效時間內獲得精確的最優解。然而,我們可以在多項式時間內求解一個重要的子問題,即給定入庫和出庫任務的操作順序,如何確定各個出庫任務對應的出庫位置。將此子問題命名為SP,并在之后利用其求解原問題。 定理2SP問題能夠在O(n3)的時間內求解出最優解,其中n為出入庫任務的數量。 證明:當給定出入庫任務的操作順序后,任意出庫任務的下一個任務有三種情況且已知。(1)當下一個任務是入庫任務時,堆垛機從出庫任務的位置出發,移動到出庫位置,再空載返回入口;(2)當下一個任務是出庫任務時,堆垛機從出庫任務的位置出發,移動到出庫位置,再空載移動到下一個任務的位置;(3)當出庫任務為最后一個任務時,堆垛機從出庫任務的位置出發,移動到出庫位置并結束。我們引入二分圖理念,節點表示為出庫任務j和出庫位置k。如有必要,我們增加虛擬任務使得出庫任務和位置的數量相等。任意出庫任務均和所有出庫位置相連,根據不同情況設置不同的邊權重cjk見表2(其中q已知)。 表2 不同情況下對應的邊權重計算公式 針對上述問題,我們可以建立整數規劃模型如下: (14) (15) (16) yjk={0,1}. (17) 目標函數(14)表示最小化總的邊權重;約束(15)和(16)表示出庫任務和出庫位置一一對應;約束(17)表示決策變量的取值范圍。此問題為指派問題,可使用匈牙利算法在O(n3)的時間內獲得最優解。 注意到SP問題本身也是實踐中的一個重要優化問題。對于入庫任務來說,需要存放的貨物會在傳送帶上等待堆垛機操作,由于很難在傳送帶上改變待存放貨物的位置,因此,入庫任務按照先到先服務的模式完成;對于出庫任務來說為及時滿足客戶訂單是許多倉庫的重要準則,因此,出庫任務通常根據到期時間排序,此時,出庫任務的取貨順序也確定。 原問題分解成為兩個子問題:(1)找到出入庫任務的最優操作順序,(2)在給定操作順序下,決策如何將出庫任務分配給出庫位置。后一個子問題可以通過求解3.1小節中的指派問題獲得最優解。為此,本文設計基于遺傳算法和指派算法的混合求解算法對模型進行求解。遺傳算法是一種通過模擬生物界自然選擇和遺傳機制的隨機搜索算法,具有收斂速度快,不易陷入局部最優等特點。具體流程如下: 3.2.1 編碼方式 編碼方式為整數編碼。入庫任務按照先到先服務方式完成,編號為1,2,…,m;出庫任務編號為m+1,…,n。采用一個n維序列表示一條染色體,即為子問題1的一個解。其中第i維上的數字為fi,表示任務fi被第i個處理。例如,圖3(a)表示有6個任務(3個入庫任務,3個出庫任務)的子問題1的一個解的編碼,在此調度方案中,堆垛機按照1-5-4-2-3-6的次序完成任務。 3.2.2 生成初始種群 定義種群規模為Npop的初始種群。考慮到入庫任務按照先到先服務方式完成,有相對完成順序的約束,在此基礎上產生初始種群。例如圖3(b)并不是可行解,因為入庫任務2先于1完成,違背約束。 圖3 編碼表示 3.2.3 計算個體目標函數 在獲得子問題1的解,即入出庫任務的操作順序(記為Ai,i=1,2,…,Npop)后,通過3.1節所提出的求解指派問題的方法確定各個出庫任務對應的出庫位置(記為Bi,i=1,2,…,Npop)。當出入庫任務順序,出庫任務對應的出庫位置均已知時,可計算出目標函數F(Ai,Bi)。 3.2.4 適應度函數 目標函數為求堆垛機完成所有任務運行總距離的最小值,因此,采用個體目標函數的倒數作為適應度函數,定義如下: fitnessi=1/F(Ai,Bi),i=1,2,…,Npop. 3.2.5 選擇 對每代個體,通過輪盤賭法進行選擇,每個個體的選擇概率為 產生一個在[0,1]之間的均勻隨機數,將該隨機數作為選擇指針確定被選個體。 3.2.6 交叉操作 采用單點交叉的方法,先從區間[1,n]中隨機抽取交叉點,子個體Offspring1在交叉點左側的基因與父個體Parent1在交叉點左側的基因相同,Offspring1缺失的基因按順序從父個體Parent2處獲得;同理獲得子個體Offspring2。由于模型對入庫任務有嚴格的順序約束,因此,為了避免產生非可行解,在交叉操作完成后增加一個步驟:不改變出庫任務的順序,將入庫任務按照編號從小到大的順序重新排序。 3.2.7 變異操作 隨機產生兩個變異點位置,交換兩個變異點位置的基因,形成新的染色體。為避免變異產生非可行解,只對兩個出庫任務,或者不影響入庫順序的一個入庫任務和一個出庫任務進行變異操作。 綜上,該算法的流程圖和偽代碼分布如圖4和表3所示。 圖4 算法流程圖 表3 兩階段啟發式算法偽代碼 實驗使用MatlabR2014a開發算法程序。由于遺傳算法的參數設置會影響算法效率,我們對參數的選擇進行多次測試,其中種群規模大小、交叉概率和變異概率的集合分別為Npop={50,80,100},α={0.7,0.8,0.85,0.9},β={0.05,0.1,0.15,0.2}。通過預先實驗獲得了一組較好的遺傳算法參數組合:Npop=50,α=0.8,β=0.15。本文制定2個遺傳算法終止規則:一是當最優目標值保持不變次數達到最大迭代數的三分之一時終止;二是算法的迭代次數達到預設的最大迭代次數時終止(本文采取文獻中常用的100次迭代)。倉庫參數設計選用Ramtin和Pazour[17],設置倉庫長為60 m,高為24 m,托盤大小為1.2 m*1.2 m。為了驗證所建立模型與本文設計的兩階段啟發式算法的有效性,對每個算例進行20次計算取平均值,并使用CPLEX求解模型,通過結果比較來驗證算法效率。所有實驗均運行在1.8 GHz Intel Core 4 CPU和8GB內存的計算機上。 針對每一個算例,分別用CPLEX和本文提出的啟發式算法求解,對比CPU計算時間和求得的結果。其中GAP1=(本文算法目標值-CPLEX目標值)/CPLEX目標值*100%,GAP2 =(FCFS方法目標值-本文算法目標值)/本文算法目標值*100%。記SN、RN和K分別表示入庫任務、出庫任務和出庫位置的數量。實驗結果如表4所示,且有以下結論:(1)當出入庫任務數量多于27個時,CPLEX已無法求解,而本文算法在所有算例中均能求出近似最優解,與CPLEX求出的最優解最多相差2.82%。同時,本文算法花費的CPU時間也非常短,求解20個任務15個出庫位置的問題只需不到6秒,運算效率遠遠高于CPLEX。綜上,本文算法在效率和有效性兩個方面上表現均較好。(2)本文提出的算法相較于先到先服務方法最大改善了25.09%,平均改善了20.47%,表明本文算法明顯優于企業中常用的先到先服務方法。 表4 算例結果對比 接下來研究出庫位置的數量變化對數值結果的影響。我們隨機產生10組出入庫任務的數量和所在位置,對于每組算例,出庫位置的數量K變化為{10,12,14,16,18,20}。使用本文提出的算法求解目標值并對10組算例取平均值。數值結果如圖5所示。我們發現隨著出庫位置數量的增加,堆垛機移動的距離從636 m逐步降低,最終保持平緩到596 m。注意到出庫位置的增加也會帶來運作成本的增長,如揀選人員的人力成本等。因此,企業管理人員需要權衡每多開一個出庫位置帶來的堆垛機移動成本的減少和其他運作成本的增加,以確定最優的出庫位置的數量。 圖5 出庫位置數量對目標值的影響 本文主要研究了一種新型自動化倉儲系統,其特征是在貨架的底層有多個出口位置以供揀選人員做訂單揀選任務。此倉儲系統將存儲和分揀任務統一于一處,既提高了空間利用率,又降低了能源消耗。本文聚焦于出入庫任務調度和出口位置選擇問題,需要同時決策出入庫任務的順序以及出庫任務與出口位置的匹配。我們提出了求解該問題的混合整數規劃模型,并將問題分解成兩個子問題:先確定出入庫任務的順序,再在給定順序的情況下決策出庫貨物釋放到哪一個出庫位置。后一個子問題可以在多項式時間內求出最優解。根據此性質我們設計了基于遺傳算法和指派問題的兩階段啟發式算法,并與CPLEX求解的結果進行比較。數值實驗的結果表明了該模型和算法的有效性。 本文可以在以下幾個方面進行擴展研究:首先,本文考慮了倉儲系統采用專用存儲策略,而針對不同的存儲策略對調度問題影響的研究對實踐也有重要的指導意義。其次,在理論方面,如何為該優化問題設計求解一個緊的下界也很值得期待。2.3 復雜度分析
3 算法設計
3.1 多項式時間求解子問題

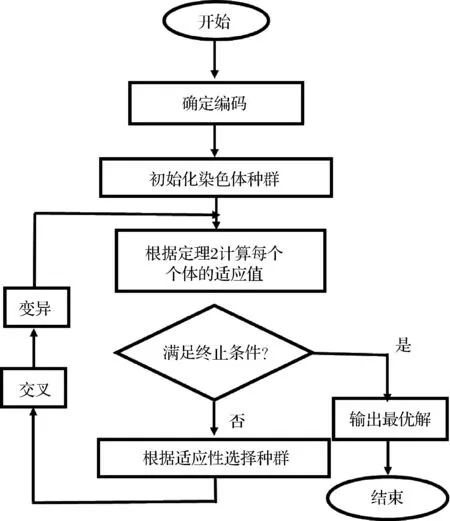
3.2 兩階段啟發式算法


4 數值實驗
5 結語

