一種可見光波段氣體傳感器的設計與研究

羅世忠， 王 琦， 孫光瑀， 張大偉

（上海理工大學 光電信息與計算機工程學院，上海 200093）

導模共振（guide mode resonance, GMR）是指外部傳播的衍射場與受調制波導的泄漏模之間產生耦合，當入射光參數或光柵結構參數發生極小變化時，光柵衍射波的傳播能量發生劇烈變化的現象[1-2]。GMR光譜具有高衍射效率和窄帶寬性質，可應用于窄帶濾光片、光學調制器和傳感器等光學器件的設計。當介質光柵附著在具有吸收特性的襯底（例如金屬材料）上時，在GMR發生時具有強烈的吸收特性[3]，反射譜中會出現窄帶的共振缺陷峰。

由于GMR傳感器具有高靈敏度、免標記、微型化以及實時檢測等優勢，將基于共振效應的器件應用于傳感領域的研究越來越多[4-5]。Hemmati等[6]通過微加工工藝，在光纖頂端制作集成的GMR結構，能夠實現約77%的光傳輸效率，同時可以實現傳感功能，其靈敏度約為200 nm/RIU（refractive index unit，RIU）。Lin 等[7]提出在全介質 GMR 傳感器結構中增加一層金屬緩沖層，可以顯著提高傳感器的靈敏度。Wang等[8]設計了一種透射式的氣體傳感器，靈敏度高達748 nm/RIU。燕山大學的陳穎等[9]提出一種用于近紅外波段的混合波導傳感結構，結構中可產生多種共振模式，模式之間相互耦合，反射譜中出現兩個窄帶缺陷峰，結構靈敏度分別為466 nm/RIU和628 nm/RIU，品質因數（figure of merit，FOM）分別可達 42.3/RIU 和78.5/RIU。

但是，當前大多研究基于共振效應的傳感結構，其品質因數并不優越，從而會影響測量結果的精確性。為了設計一種具有較高FOM的傳感結構[10]，本文提出一種應用于可見光波段的混合波導結構，在結構中產生導模共振模式，反射光譜中出現4個共振缺陷峰，其中3個共振峰擁有較好的FOM，可以用于氣體傳感，利用多孔硅的折射率可調特性，能夠實現待測氣體濃度的動態測量。

1 結構建立與設計原理

1.1 結構建立

圖1為亞波長介質光柵/介質波導/金屬襯底結構模型（yz面截面圖），該結構從上至下依次為介質光柵層、電介質層和金屬層（當結構參數一致，將襯底材料換為電介質時，該結構的靈敏度基本不變，但其品質因數明顯降低）。根據Lin等[7]的研究，該現象可歸因于金屬層對倏逝波的調制作用，GMR傳感器是一種高諧振器件，必須很好地滿足波導的高約束條件，金屬由于反射率高，可以將光反射到任意方向，在任何傳播角度都可以很容易實現對高品質因子共振的約束。采用的結構參數為：光柵層材料為二氧化鈦（TiO2）；光柵周期為Λ=430 nm；光柵脊寬度為w=180 nm；厚度為dg=40 nm；外部環境氣體為空氣，折射率為nc=1；選用多孔硅作為電介質材料，厚度為dw=725 nm。由Bruggeman等效介質理論[11]可知，當多孔硅的孔隙率為71.8%時，其等效折射率為nw=1.5；金屬襯底選用金屬銀，其介電常數由Lorentz-Drude模型描述。

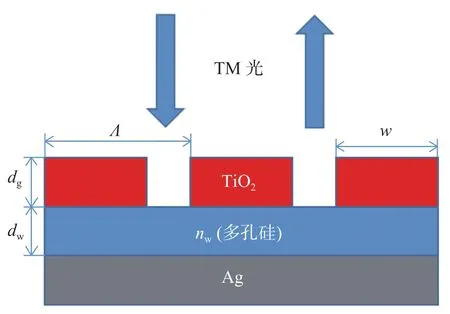
圖 1 混合波導結構模型Fig.1 Structural model of the hybrid waveguide

該研究利用時域有限差分法（FDTD）對所提結構的光學特性進行研究，結構參數如表1所示。采用FDTD Solutions軟件對該結構進行模擬分析，以一個光柵周期為一個單元，TM模式光垂直入射到光柵表面，收集反射光（平行于入射光），分析其光學特性。

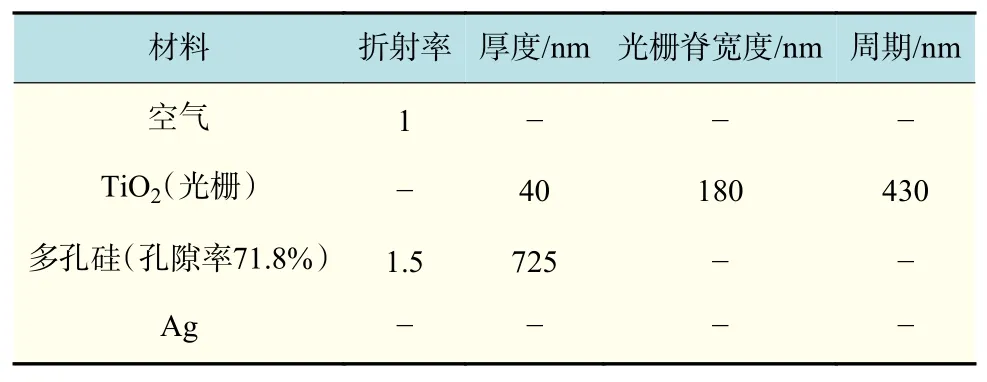
表 1 結構參數表Tab.1 Structure parameters

1.2 設計原理

光柵可以看作是周期調制的波導，當光柵的高級次子波與波導所支持的導模在參數上接近時，光柵的能量重新分布。由于光柵的周期調制性使得光柵波導有泄漏，因而泄漏能量也重新分布形成導模共振效應。根據光波導理論，光柵層等效的光波導與第j級消逝波的有效傳播常數β可以表示為：

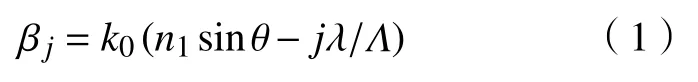
式中：n為介質折射率；θ為折射角；λ為入射光波長；k0=2π/λ。

該式表明第j級消逝波與導模相位匹配時，能夠產生導模共振[12]。根據導模共振的約束條件，在非正入射條件下，共振峰將會分裂成兩個，單通道結構演變為雙通道結構[13]。本研究提出的結構為四通道導模共振結構，能夠同時調諧4個波長的光，與傳統的單通道結構相比，該結構可以簡化光學系統，減輕系統的負荷[14]。

王振華等[15]提出增加緩沖層可以得到多通道的濾波結構，在保持光柵參量以及其他參量不變的情況下，只改變緩沖層的厚度，隨著緩沖層的厚度改變，波導所支持的模式將會增加，將會出現更多的共振峰。此外，共振結構的反射率也會隨著緩沖層厚度的改變而改變。

根據時域有限差分法，采用FDTD Solutions在單層導模共振結構的基礎上，增加一層介質層充作緩沖層，優化結構參數，獲得了光學特性較好的四通道結構。

2 傳感特性分析

采用FDTD Solutions軟件進行計算得到該結構的反射光譜，如圖2所示，在可見光波段得到4個共振缺陷峰，λ1為 436.072 nm，λ2為 486.675 nm，λ3為 554.309 nm，λ4為 609.921 nm。

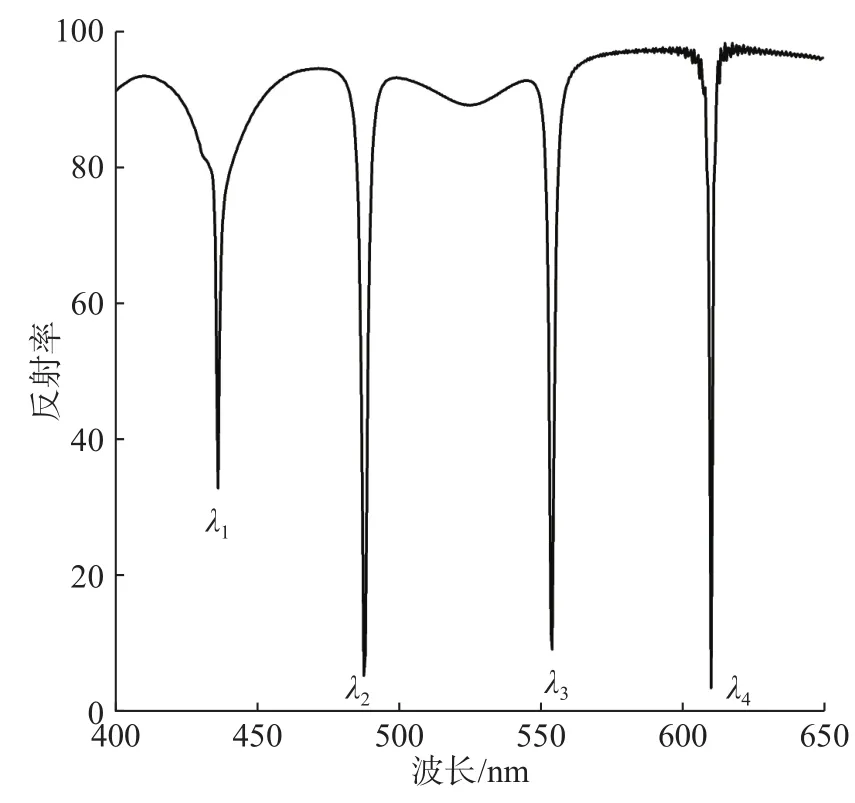
圖 2 傳感結構反射光譜Fig.2 Reflection spectrum of the sensing structure

同時，對共振缺陷波長處的電場進行了模擬計算，觀察結構中的共振情況，圖3為4個共振波長的電場分布圖：圖（a）中能量集中分布在光柵脊兩側；圖（b）中能量分布在結構各層，但光柵與介質層接觸面處的能量更集中，電場強度最大；從圖（c）可以看出，電場主要分布在介質層內部，且最大電場強度高于圖（b）中數值；從圖（d）可知，當共振波長為609.9 nm時，能量高度集中在介質層內部，電場強度達到最大，且分布在光柵兩側，說明該處的共振效應最強。

圖 3 不同共振波長處的電場分布圖Fig.3 Electric field distributions at different resonant wavelengths

該結構采用多孔硅充作波導層介質，在進行氣體濃度測量時，當多孔硅的孔隙內吸附一定濃度的待測氣體時，多孔硅的有效折射率會隨著氣體濃度的改變隨之發生變化[16]，使得結構光學響應特性發生變化，因而該結構能夠實現待測氣體濃度的動態測量，例如折射率較高的甲醛氣體等。將傳感結構放置于一定濃度的待測氣體中，通過分子的自由運動，待測氣體擴散到多孔硅的孔隙中，當傳感結構內外氣壓穩定時，多孔硅的有效折射率發生相應變化，其變化規律遵循Bruggeman介電函數近似模型[17]：

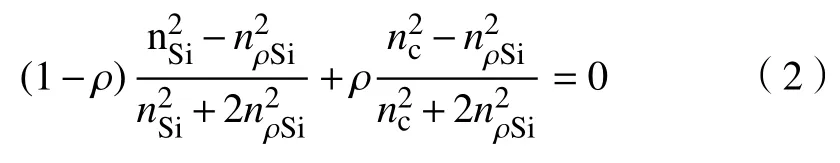
式中：nSi為硅的折射率；nρSi為多孔硅的等效折射率；ρ為多孔硅的孔隙率；nc為空氣折射率。為了進一步研究該結構傳感特性，以0.01為步長，將多孔硅的有效折射率增加到1.55，得到圖4所示的光學響應曲線。從圖4可以看出，隨著多孔硅有效折射率的增加，共振峰向長波長方向漂移。當其折射率從1.5增加到1.55時，共振峰1漂移到 446.092 nm，半高全寬（full width at half maximum，FWHM）為 3.5 nm，其波長靈敏度（S=Δλ/Δn，Δλ為共振波長變化量，Δn為折射率變化量）為200 nm/RIU，品質因數（FOM=S/FWHM）達到 57.1/RIU；峰2漂移到501.703 nm，半高全寬為2.5 nm，靈敏度為300 nm/RIU，品質因數為120/RIU；峰3漂移到571.841 nm，半高全寬為2.3 nm，靈敏度為350 nm/RIU，品質因數為152.2/RIU；峰4漂移到 629.96 nm，半高全寬為 1.3 nm，靈敏度達到400 nm/RIU，品質因數達到307.7/RIU。

圖 4 多孔硅不同折射率時共振波長漂移Fig. 4 Resonant wavelength shift of porous silicon with different refractive indexes

此外，本文還研究了共振波長差隨著多孔硅折射率增加的變化情況。這里，共振波長差定義為λi+1–λi（i=1,2,3，定義為波長差的階次），即高階共振波長減去次階共振波長的差值，結果如圖5所示。不難發現，隨著多孔硅的折射率增加，3個階次的波長差均在逐漸增大，而且，階次越高，波長差值隨著折射率增加的變化范圍越小。

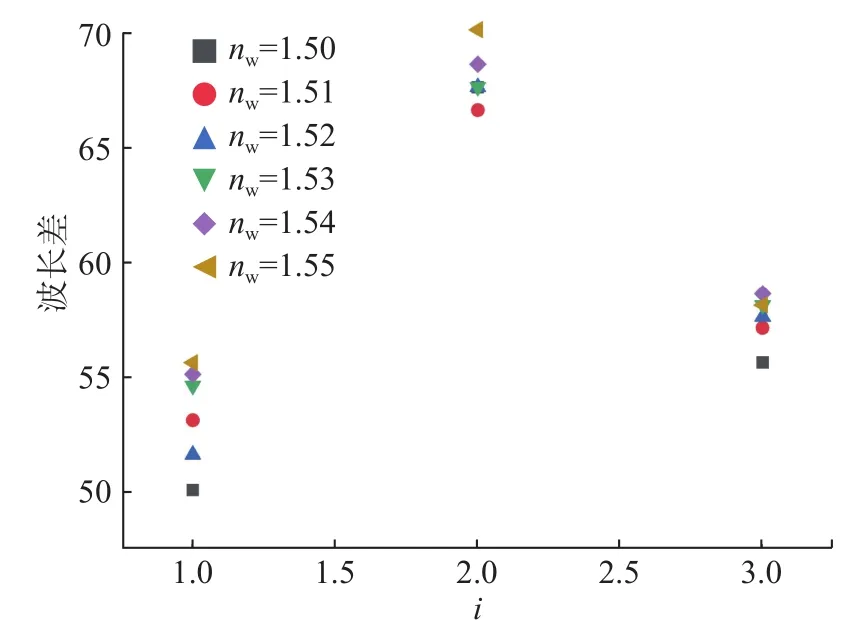
圖 5 多孔硅不同折射率時共振波長差Fig.5 Resonant wavelength difference of porous silicon with different refractive indexes

本文提出的結構能夠得到4個共振缺陷峰，其中，共振峰2，3，4具有優異的傳感特性，表現出高品質因數和高靈敏度。與燕山大學的陳穎等人提出的傳感結構相比，前者靈敏度分別可達466 nm/RIU 和 628 nm/RIU，品質因數較低。較于前者，該結構的靈敏度雖然較低，但品質因數極為優越，在進行氣體濃度測量時，誤差更小，測量結果更加精確。而且該結構適用于可見光范圍，無電磁輻射，成本低，頻譜豐富。此外，可見光傳感器的光譜響應接近人眼函數曲線，能夠透過可見光，過濾紫外線以及中遠紅外光，增強了光學濾波效果。

3 結 論

設計了一種一維亞波長介質光柵/多孔硅/金屬襯底的傳感結構，該結構可以產生導模共振，利用FDTD進行參數掃描優化，在反射光譜中形成4個窄帶共振缺陷峰。其中3個共振峰表現出優異的傳感性能，品質因數分別達到120，152.2和307.7/RIU，檢測精度高，皆可用于氣體傳感。該研究能夠為氣體檢測以及空氣污染監測提供一定的參考價值。