珠江上中游社會-水文多因素的系統動力學生活需水預測

易 彬，陳 璐，路嵐青，覃葉紅萍

(1. 華中科技大學水電與數字化工程學院，武漢 430074；2. 數字流域科學與技術湖北省重點實驗室，武漢 430074)

0 引 言

隨著世界經濟迅速發展、全球人口加速膨脹、城市化進程普遍加快，世界各地對水資源的需求日益增長。水資源短缺已成為影響世界政治格局、經濟發展和社會進步的重要瓶頸問題，其本質在于供給和需求的矛盾和不平衡。聯合國數據估計，人類的需水量在兩個世紀間發生了深刻變化，自20世紀初期，全球用水量僅4 000 億m3/a，到20世紀末期，已上升至39 000 億m3/a。因此，考慮人口增長、經濟發展、城市化進程等社會經濟因素，開展系統深入的生活需水預測研究，對保障社會經濟可持續發展具有重要的現實意義。

需水預測的方法主要有時間序列法[1,2]、回歸分析法[3,4]、灰色系統法等[5]。在上述方法中，回歸分析法較為成熟，已廣泛應用于工程實踐，但該方法預測效果依賴于原始數據的長度和可靠性，此外，該方法存在需水預測因子與需水量必須高度相關的局限[6]。針對上述缺陷，灰色系統法、人工神經網絡法[7]等黑箱建模方法應運而生，但該類方法要求原始數據在時間尺度上呈指數變化規律，換言之要求數據總體上變化趨勢一致，在量級上無大波動，不存在周期性、無序性和突變[8]。然而，實際中大多數需水預測因子呈S型增長[9]，因此系統黑箱模型的預測結果往往偏大。系統動力學方法是現階段常用的一種需水預測方法，該方法是在反饋控制理論基礎上，用計算機仿真的手段研究社會經濟系統與水資源問題之間關系的一種定量與定性相結合方法，適合處理長期性、周期性等問題。

為厘清社會經濟發展與生活用水量的本質關系，研究引入了社會水文學基本概念，融合了自然、人口、經濟、環境和人類意識等一系列影響因素，提出了耦合社會-水文多因素的生活需水系統動力學建模方法，辨識了影響生活需水量的關鍵社會經濟因子，構建了社會-水文相關因子與生活需水量互饋耦合網絡拓撲圖，建立了生產需水系統動力學差分和微分方程組，實現了自然、社會雙重驅動下的生活需水預測。

1 影響生活需水的主要社會經濟因子辨識

人口規模、生活水平提高導致了居民收入、水價、節水意識的提升以及城鎮化進程的加快，這些因素都會導致生活需水量的變化[10]。楊亮等[11]認為人口規模的擴大對水資源損耗的增長具有顯著影響。張曉曉等[12]指出城鎮人口每增加1萬人，城鎮居民生活用水量將增加20.91 萬m3。因此本文將人口和城市化水平作為影響生活需水變化的重要因素。

此外，城鄉居民收入水平與該地區的生活需水量也有密切關系，隨著人們消費支出的提高，更多支出將轉移到高耗水型消費行業，如伴隨居住環境升級以及衛生習慣改善(人類的意識行為)，城市居民用水需求在邊際上出現遞增趨勢。馮業棟等[13]發現經濟因素對居民用水量的影響遠超預期；姚遠[14]認為水價、人口及居民人均年收入是決定用水量的重要因素。

綜上所述，研究把常住人口、城鎮化率、城鄉居民收入、節水意識、水價等作為影響生活需水量的重要因素。

2 影響生活需水量的社會經濟因子演化規律解析

2.1 馬爾薩斯-邏輯回歸人口預測模型

馬爾薩斯人口增長模型是一種經典人口預測方法，其表達式為：

P(t)=P(t0)er(t-t0)

(1)

式中：P(t)為時刻t的人口；P(t0)為初始時刻t0的人口；r為人口增長率。該模型認為人口將持續成指數增長，當t趨于無窮時，人口也趨于無窮。

事實上，隨時間推移，一個地區空間、食物和生育能力會限制本地區的人口，以至于最終該地區人口會趨于穩定，人口增長存在一個閾值，因此，該模型已不再適用。

因增長率是變化的，人口變化過程可用數學公式描述如下：

(2)

求解得：

(3)

式中：N為人口增長閾值。

該模型為馬爾薩斯-邏輯回歸模型，本文采用該模型進行區域人口的預測。

2.2 Logistic曲線城鎮化率預測模型

Logistic曲線估算法是現階段最為常用的城鎮化率估算方法，具體表達式如下：

(4)

式中：δ代表城市化率；C為積分常數；d為待確定參數。

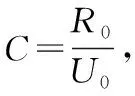
2.3 線性回歸居民收入預測模型

城鎮、農村居民可支配收入預測旨在探討收入增加對居民生活用水需求的影響，選擇線性曲線對地區城鎮、農村可支配收入進行模擬，具體模型表述如下：

(5)

式中：RPIt、UPIt分別代表第t年時的農村、城鎮居民人均可支配收入；RPI0、UPI0分別為研究基期t0的農村和城鎮居民人均可支配收入；k1代表農村居民人均可支配收入增長率；k2代表城鎮居民人均可支配收入增長率。

2.4 居民節水意識預測模型

隨著經濟增長，居民生活水平不斷提高，對家庭生活用水的需求會增加，但在節水教育的普及下，居民素質不斷提高，相應的生活需水量增量會放緩，主要驅動原因如下：① 居民家庭節水型器具使用量增加，導致用水量減少；② 培養好的生活用水習慣導致用水量減少(減少淋浴時間，減少洗滌劑用量)；③ 合理重復利用生活用水導致用水量減少。相對于水價的提升對生活用水的影響，提高居民節水意識對生活用水量的變化更加明顯。在此背景下，本研究提出了節水意識數學描述方法，有效模擬了節水意識對生活用水量的影響。

在理想狀態下，假設節水意識K呈線性增長(0≤K≤1)，節水意識年增長率θ保持不變，可用以下數學模型表示：

(6)

在實際生活中，居民節水意識實際增長過程是非線性的。近年來，居民素質上升明顯，節水意識處于快速提升階段，但這種提升并不是無節制的，到達一定程度時，上升速度會逐漸放緩，呈現出由快到慢的特征，并逐漸趨近于節水意識上限。基于上述分析，對節水意識數學模型做出如下定義：

(7)

式中：K代表節水意識；θ代表節水意識增長率；M代表節水意識上限。

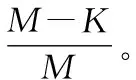
(8)

求解方程得：

(9)

具體確定步驟為：① 節水意識上限參數M的確定，M的取值范圍為[0,1]，首先設M=1；② 參數A的確定，對于基準年，t=0，根據式(9)，K=M-A，假設A的取值在[0,M]之間，不同A值，則得到不同K值；③ 將不同K、M、A值代入需水預測模型，與歷史需水量擬合誤差最小的A值，即為所求。若當M=1時，無法擬合最優，可調整M的值，按照上述步驟，重新率定，直到擬合結果較優為止。

2.5 居民水價預測模型

水價是影響生活需水量的重要指標，城市水資源供需矛盾的凸顯加劇了水安全危機，增強了水商品意識，通過水價的經濟杠桿作用促進節約用水已經成為社會共識[15]。隨著社會經濟不斷發展，生活用水水價呈現穩定上升趨勢，研究擬采用分段線性函數模擬水價的變化過程，具體模型如下：

(10)

式中：PTi(i=0,1,2,…)代表Ti與前一時間節點間的水價均值。

3 耦合社會-水文多因素的系統動力學生活需水預測模型

根據建立的馬爾薩斯-邏輯回歸人口預測模型、Logistic曲線城鎮化率預測模型、線性回歸居民收入預測模型、節水意識預測模型，首先預測常住人口、城鎮化率、城鎮及農村人均可支配收入、節水意識的未來演化趨勢；構建影響生活需水量的社會經濟因素因果關系圖(如圖1所示)，依據各變量的因果關系，建立耦合社會-水文多因素的生活需水系統動力學模型，模型表達式如下：

(11)

式中：ΔURWD、ΔRUWD、ΔDWD分別為城市生活需水增量、農村生活需水增量、生活需水總增量；DWDt代表第t年的生活需水量；DWDt-1代表t-1年的生活需水量；UPI代表城市居民人均收入；RPI代表農村居民人均收入；ΔURP代表城鎮人口增加值；ΔRUP代表農村人口增加值；ΔTPK代表總人口增加值；Δδ代表城鎮化增長率變化值；P代表生活用水水價；χ代表居民收入彈性系數；φ1代表農村人口增量調節系數，表示農村人口變化對生活需水的影響程度；φ2代表城鎮人口增量調節系數，表示農村人口變化對生活需水的影響程度；φ1、φ2分別表示農村、城市生活用水水價彈性系數；K代表節水意識。

為進一步解析式(11)的物理意義，提取圖1中主要因素對生活需水量的影響關系圖，如圖2(a)所示。歷史研究表明，生活需水量與居民生活購買力系數(即居民可支配收入與生活用水水價的比值)存在顯著相關性[16]。在此基礎上，研究提出式(11)中第1、第2式，由圖2可知，其表征了城市、農村生活需水增量 和 與城市人口增加值 (或城市化導致的農村人口減少值 )、人均可支配收入PI、生活水價 等多種因素的定量映射關系。由圖2(a)可知，人口增量、人均可支配收入對生活需水量呈現正反饋態勢，居民水價對生活需水增量呈現負反饋態勢。通過式(11)可模擬多種因素對生活需水量改變的綜合影響。式(11)中第3式表征了生活需水量總增量等于城市需水量增量加農村需水量的增量，為避免生活需水預測出現偏大趨勢，研究以居民節水意識對城鎮、農村生活需水增量進行修正，即節水意識加強，生活需水量增速變緩[如圖2(b)所示]，進一步，得到地區生活需水總增量。最后，根據式(11)中第4式通過第t-1年生活需水預測值和生活需水增量計算第t年生活需水量預測值。

4 實例研究

4.1 研究區域概況

本文以珠江上中游為例開展例證研究。珠江上中游由梧州站點以上地區組成，隸屬于珠江水資源一級區。地處東經103°09′～111°40′北緯3°41′～26°49′之間，面積為30.43 萬km2，珠江上中游包括南北盤江、紅柳江、郁江、西江等水資源二級區。涉及區域大部在廣西、云南、貴州省份，小部分在越南諒山，具體如表1所示。以下的研究的基準期為2007年。

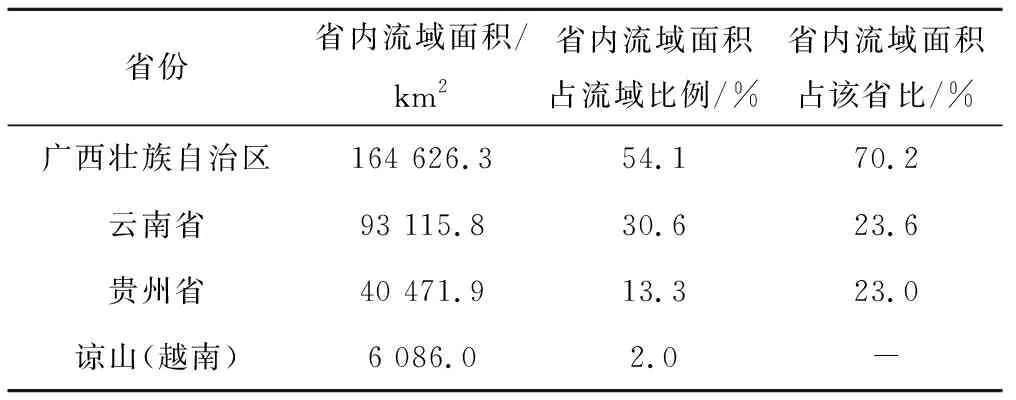
表1 珠江上中游涉及地區及面積比Tab.1 The area and area ratio of the upper and middle reaches of the Pearl River

4.2 影響生活需水量關鍵指標的預測

采用式(11)建立珠江上中游需水預測模型，分別采用所提馬爾薩斯-邏輯回歸模型、Logistic模型、線性回歸模型、節水意識模擬函數、分段線性函數進行上述因子模擬，各模型參數列于表2。

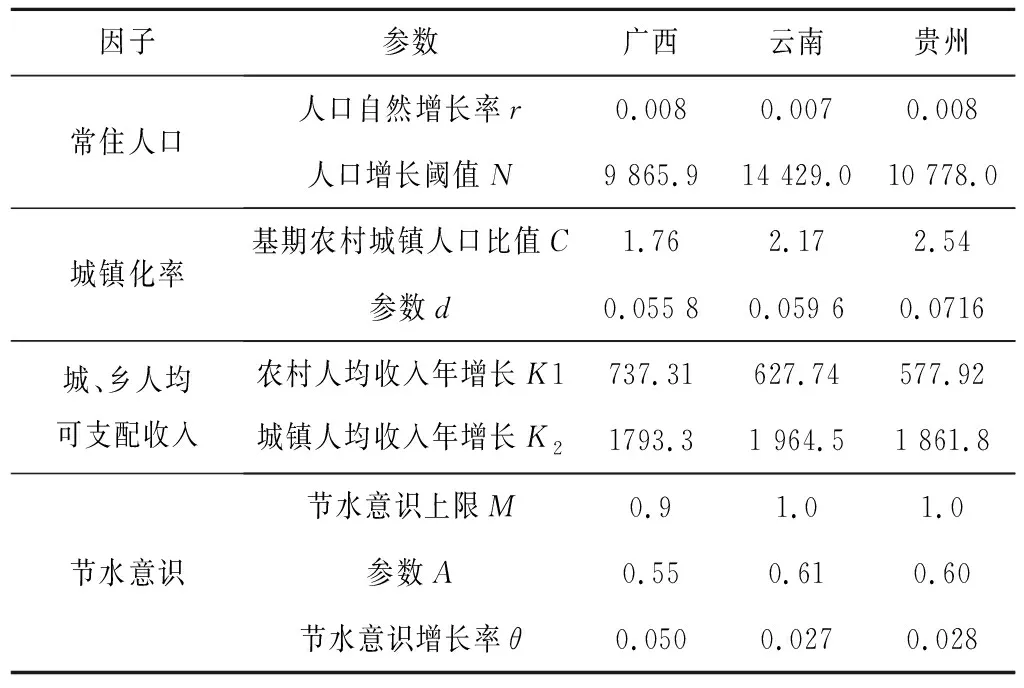
表2 需水預測模型參數表 Tab.2 Parameter table of water demand prediction model

4.2.1 珠江上中游人口預測結果

珠江上中游地區人口采用馬爾薩斯-邏輯回歸方程預測，P(t0)為基準期人口數量，首先，參考各地區人口增長規劃值確定研究區域人口自然增長率r；然后，假設不同的人口增長閾值，將人口自然增長率r、基準期人口數量代入模型，可得到人口預測值，以人口經驗值與預測值擬合最優為準則，確定人口增長閾值N。綜上，珠江上中游流域涉及廣西、云南、貴州三省的人口自然增長率取值分別為0.8%、0.7%、0.8%；人口增長閾值根據人口自然增長率進行確定，其具體依據為人口自然增長率條件下，人口經驗值與模擬值離差平方和最小，模型參數見表2，采用式(3)對珠江上中游的人口進行模擬，模擬結果及相對誤差如圖3(a)所示，可知，云南省和貴州省人口模擬值與實際值相對誤差都在2%以內，廣西模擬誤差略大，但誤差仍在5%以內。因此，人口模擬結果較好，該模型可用于未來人口演化趨勢預測。

4.2.2 Logistic曲線城鎮化率預測模型

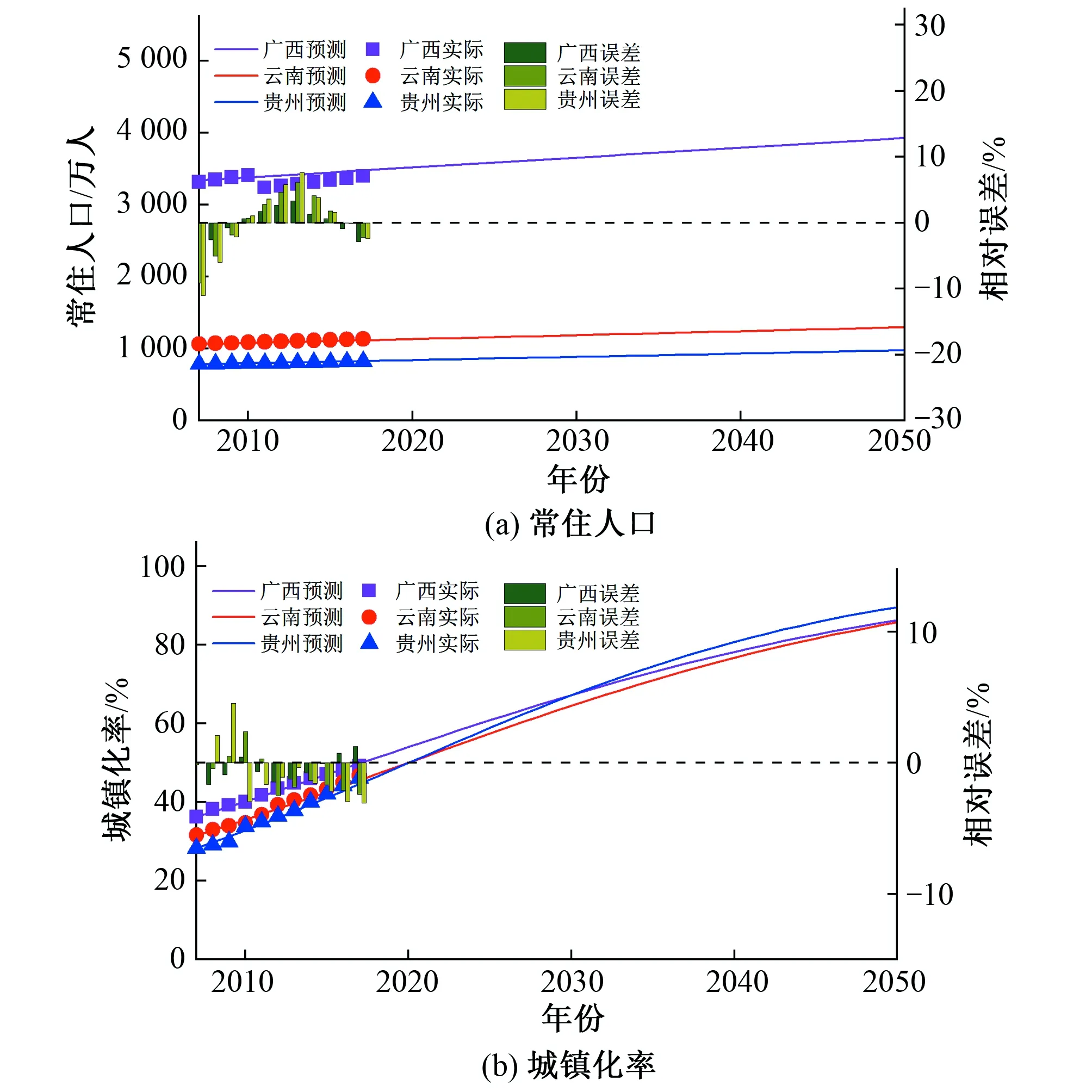
圖3 珠江上中游流域人口和城鎮化率模擬圖Fig.3 Simulation diagram of population and urbanization rate in the upper and middle reaches of the Pearl River Basin

4.2.3 基于線性回歸的居民收入預測模型

根據式(5)，采用線性模型建立各省農村及城鎮居民可支配收入預測模型，其參數采用最小二乘法確定，參數結果如表2所示，采用所建模型對珠江上中游流域各區域城鎮化發展狀況進行模擬，其模擬值與實際值及二者的相對誤差見圖4，由圖4可知，所建模型與實測值擬合效果較好。

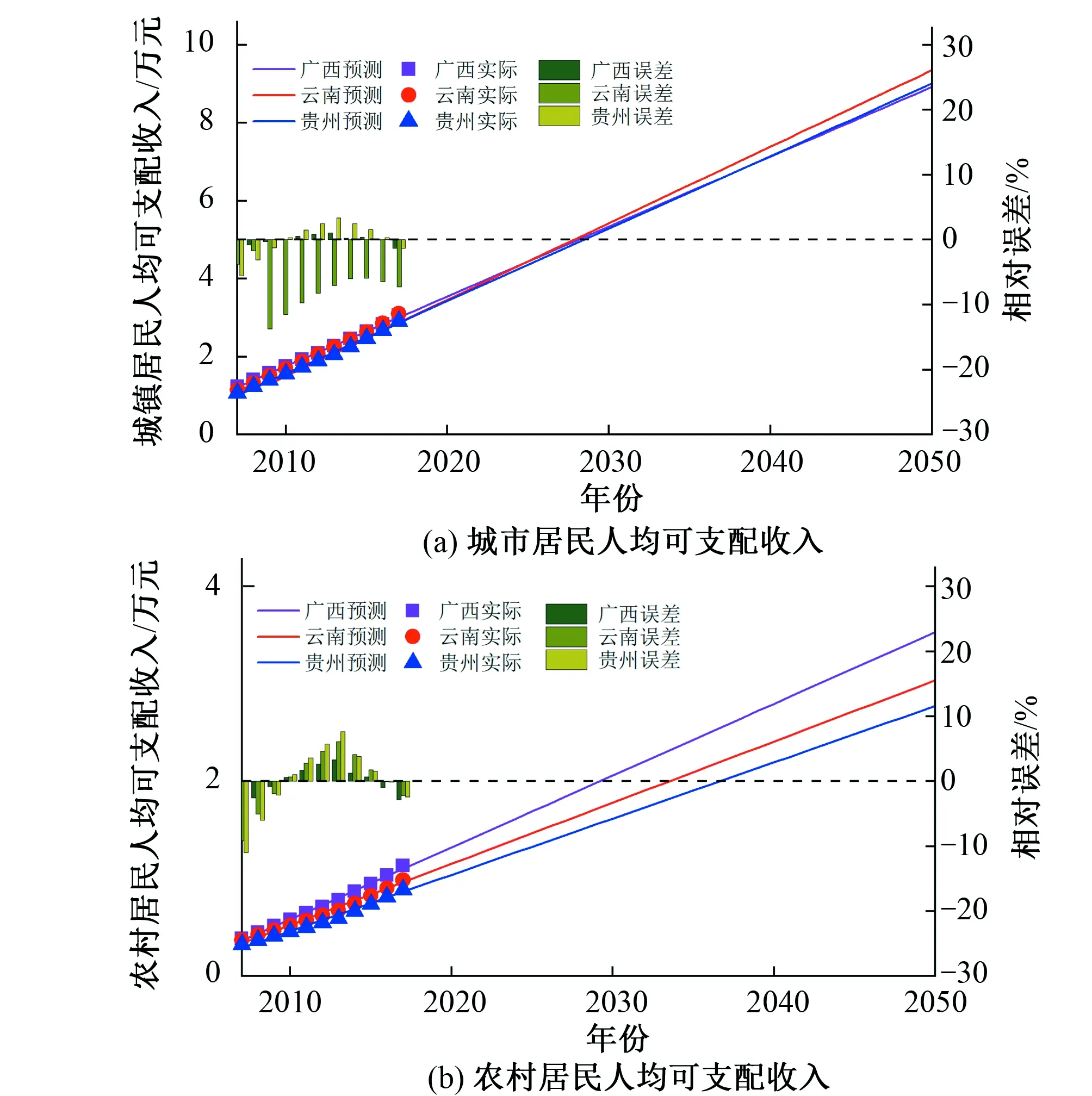
圖4 珠江上中游流域農村、城鎮人均可支配收入模擬圖Fig.4 Simulation diagram of per capita disposable income of rural and urban areas in the upper and middle reaches of the Pearl River

4.2.4 節水意識預測模型

因各省需水增長趨勢、經濟發展水平、水資源富集程度不一，各省節水意識模擬結果也不盡相同。因節水意識無歷史值可供參考，研究以試錯法率定節水意識方程的參數值。由上述方法，確定的K、M和A值如表2所示。根據上述建的各省節水意識預測模型，對珠江上中游進行居民節水意識預測，預測結果如圖5(a)。預測結果表明廣西部分居民節水意識起點較低，2007年為0.35，但是增長速度較快，2050年，其節水意識達到0.85，超過云南、貴州兩省；云南省、貴州省節水意識增長曲線類似，2007年，兩省節水意識都在0.4，到2050年，兩省節水意識都將達到0.8左右。從2007年到21世紀中期，隨著國家綜合實力提升迅速，國民素質提升較快，因此，節水意識在2030年之前增長較快，截至2030年，3個省節水意識基本達到0.6以上，2030年之后的20年間，居民節水意識仍在緩慢增長，到2050年，我國已經建成社會主義強國，各項發展趨于穩定，珠江上中游居民節水意識經過30年的發展達到中等偏上水平。

4.2.5 水價模擬

各省歷史水價均值以該省典型市縣水價為標準進行計算，其中廣西、云南、貴州三省歷史水價均值分別為2.55元、3.45元和2.7元，以社會經濟發展節點2020、2030、2050年為水價變化節點，李翠梅等[17]發現節水效果并非隨水價的上升穩定增加，當水價范圍在3～5元之間時，節水量呈明顯下降趨勢，因此研究假定各時間分段間水價增幅為20%，各省水價格如表3所示。

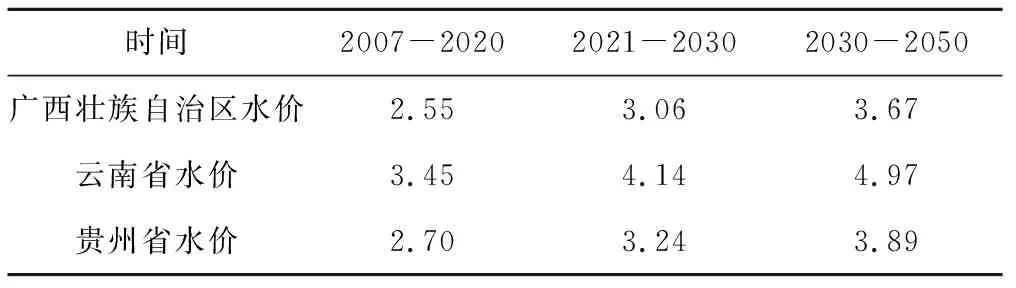
表3 珠江上中游流域水價格模擬 元

4.3 珠江上中游生活需水預測

本研究采用歷史檢驗法驗證需水預測模型的效果，將模擬值與真實值進行對比，計算兩者相對誤差。珠江上中游各省生活用水實際值和模擬值誤差結果如圖5(b)所示。檢驗結果表明，各地區模擬值和歷史值比較有偏大趨勢，各省生活需水的歷史模擬總體誤差在10%以內，個別年份誤差超過該值，原因是各地區存在人口突變或者政策變更，導致的用水統計資料未能保持同步造成。因預測期長達30年，政策的變更均存在未知情況，僅能根據歷史資料預測得到未來各因素的大體趨勢，因此，模型的模擬結果可反映各省生活需水的發展和演化規律。具體地，珠江上中游流域生活需水總體呈上升趨勢，但上升趨勢不明顯，珠江上中游地區未來生活需水增量較小，總體趨勢平穩。其中，廣西部分生活需水量由2007年的27.08 億m3上升到2050年的31.33 億m3；云南部分由4.71 億m3上升至6.18 億m3；貴州部分生活需水由3.57 億m3增至5.55 億m3。

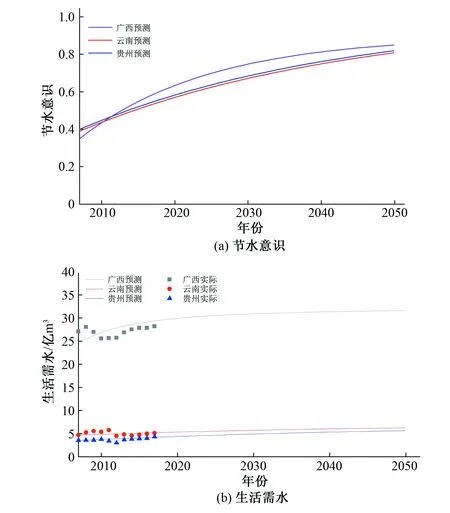
圖5 珠江上中游流域各省節水意識和生活需水模擬Fig.5 Simulation of water-saving consciousness and domestic water demand in the upper and middle reaches of the Pearl River Basin

4.4 與現有模型的比較分析

用水配額法已廣泛應用于生活需水預測研究中。研究分別采用用水配額法和所提系統動力學方法預測珠江上中游的生活需水量，結果如表4所示。預測結果表明，生活需水配額法在檢驗期，相對誤差都為正值，由此可知預測結果系統性的高于實際值。經計算，用水配額法和系統動力學法的平均相對誤差分別為5.16%和7.23%。因此，系統動力學預測方法的預測效果要優于生活需水配額法。

4.5 珠江上中游生活需水預測結果

綜上，可以用上述生活預測系統動力學模型對珠江上中游地區進行生活需水預測，采用該模型模擬出2007-2050年的珠江上中游流域內生活需水量，2020、2030、2040、2050年的生活需水預測結果如表5所示。預測結果表明，2020-2030年10年間研究區域生活需水量增加了1.79 億m3，2030-2050年20年間，生活需水增加1.61 億m3，表明隨著經濟發展到一定程度，生活需水量不會隨著人口的增加無節制增長，生活需水增長趨勢會受到相關影響因素的制約而處于相對穩定狀態，如科技的發展可以提高水資源利用率，水價的增長可以促進用水節約，國民素質的提高及居民節水意識的增強，都會一定程度降低生活用水量，這與我國發展規劃相符，也和目前發達國家用水趨勢一致。

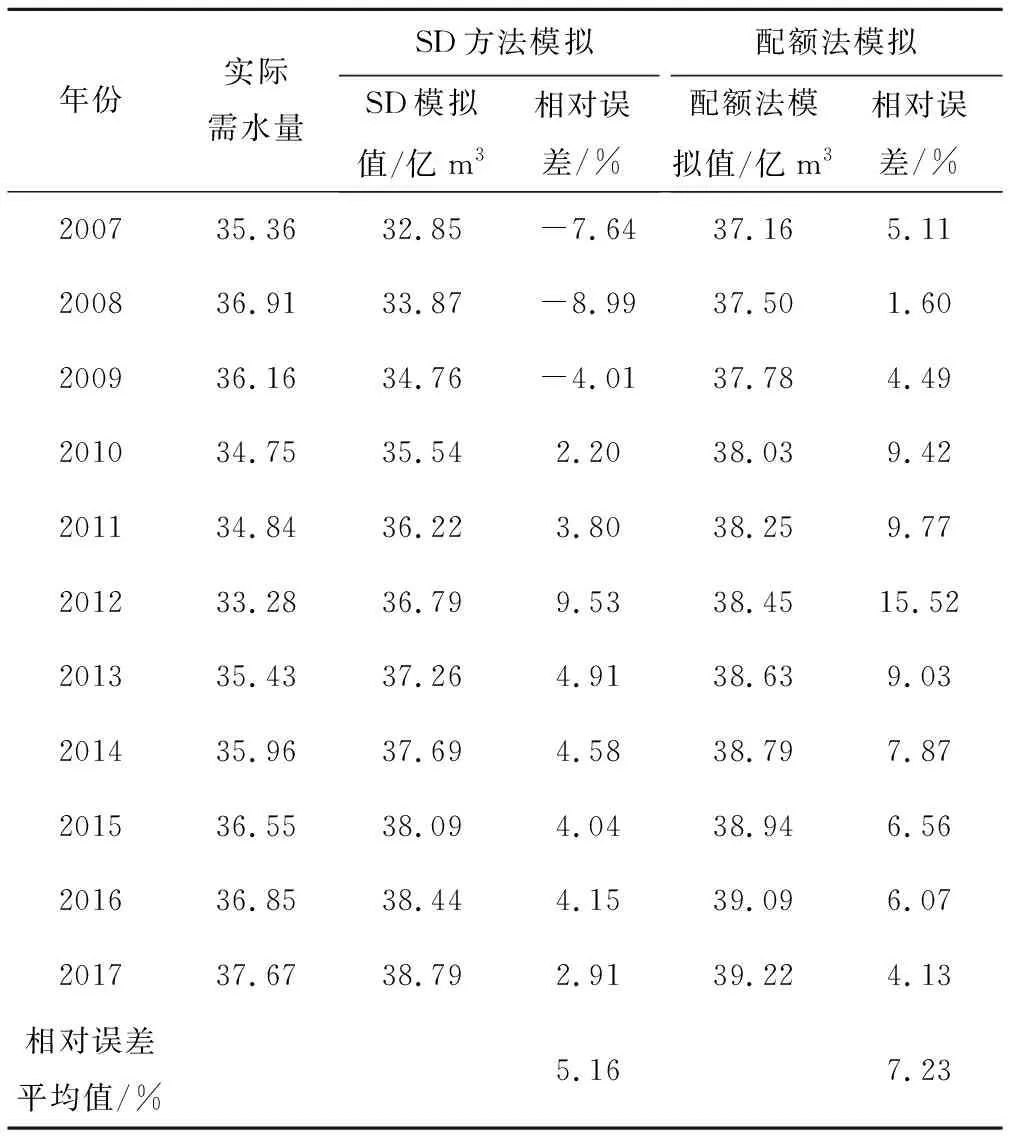
表4 配額法和系統動力學方法預測誤差分析Tab.4 Prediction error analysis of quota method and system dynamics method

表5 珠江上中游未來生活需水預測值Tab.5 Forecast results of future domestic water demand in the upper and middle reaches of the Pearl River

5 結 論

研究提出了耦合社會-水文多因素的生活需水預測系統動力學方法，辨識了影響生活需水的關鍵社會、經濟因子，揭示了人口、城鎮化率、收入水平的長期演化趨勢，首次提出了刻畫節水意識演化規律的預測方程，在此基礎上，建立了珠江上中游地區生活需水系統動力學模型。主要結果匯總如下：

(1)影響生活需水關鍵社會、經濟因子預測結果表明，各因子歷史值與模擬值擬合誤差小，預測模型能較好反映珠江上中游地區的社會、經濟和節水意識等的變化趨勢。

(2)珠江上中游地區生活需水系統動力學模型預測結果表明，歷史值與生活需水預測值較為接近，采用該模型進行未來生活需水預測是合理的，未來研究區域生活需水呈緩慢上升趨勢，用水情勢總體保持穩定。

(3)將所提方法與現有需水配額法進行比較分析，結果表明所提方法預測誤差較小。