VoLTE業務IP承載網潮汐流量預測模型建模與分析

于增源

(中國移動通信集團終端有限公司黑龍江分公司，黑龍江 哈爾濱 150028)

0 引言

網絡流量預測問題，一直是通信行業面臨的重要問題。要想明確地了解網絡性能和負載，提升網絡可用性，保證網絡安全，離不開可靠的網絡預測技術。因此，流量預測技術廣受各界關注，很多企業和供應商都已經在流量預測領域投入了大量資源進行研究。如文獻[1-2]中，流量預測不能單純利用泊松模型，而需要建立更為復雜準確的模型。目前主流的流量預測模型一般可分為2類：線性模型和非線性模型。其中，線性模型一般采用短相關的自回歸模型、自動回歸滑動模型和差分自回歸滑動平均模型等；而主流的非線性模型則包括小波預測模型、分期布朗模型等。這幾種模型目前的預測能力相對較好，但也有其巨大的局限性。IP承載網網絡流量情況一般是數據量龐大且極其復雜的，包含很多相關性及其他影響因素，但是采用以上幾種方法時，由于預測的數值區間很大，會導致預測的誤差不斷累積，最終的誤差會極大，對于刻畫承載網流量變化情況是很困難的[3]。此外，根據文獻[3-4]，流量統計和預測也深受地域以及時間影響，在偏僻地域數據流量消耗明顯要小于繁華地帶，不同地區的流量消耗也會隨著季節、節日以及每日時間的變化而呈現復雜的變化趨勢。

對網絡流量的負載水平評估和預測也是一個關于時間的數組序列問題，需要根據不同時間在同一地點采集一定時間的網絡流量數據，并根據已經采集的數據計算出未來某時刻的流量數據。根據文獻[5]，一般來講，網絡流量分布被認為是服從泊松分布，亦或是被認為是馬爾可夫過程。大部分網絡業務被定義為泊松分布，但是在文獻[6]中說明，采用泊松分布構建網絡模型是有缺陷的，因為采用這種方法會喪失網絡的自相關性特點，所以使用泊松模型會導致對流量的評價不夠準確。此外，網絡預測方法中還有一種應用較為廣泛的方法，也就是深度學習算法，例如神經網絡方法，該方法經過改進和融合后有較強的數據處理能力，并且更加靈活。根據文獻[7]和一些實驗數據可知，采用神經網絡的非線性算法一般比線性算法的預測準確率相對更高。

隨著人工神經網絡的發展，流量預測技術也開始可以與眾多的神經網絡模型相結合，解決數據處理與預測的問題。如文獻[8]所述，人工神經網絡利用計算機模擬人腦的神經系統，采用不同的數學模型如卷積神經網絡(Convolutional Neural Networks，CNN)等來處理復雜的數據問題，具有很強的學習能力。常在數據處理中應用到的人工神經網絡模型包括多層感知機、受限玻爾茲曼機等，多層感知機的網絡結構是全連接的，其結構是由多個輸入最終匯總到一個輸出上，最終獲得輸出數據集。

在人工神經網絡的不斷發展中，神經網絡越來越復雜，中間的隱藏層也越來越多，會導致嚴重的梯度消失問題。通過研究，不斷產生了新的傳遞函數來代替之前常用的Sigmoid函數。在這之后，各種新的神經網絡模型如CNN、循環神經網絡(Recurrent Neural Network，RNN)以及深度神經網絡(Deep Neural Networks，DNN)等，更廣泛地應用于圖像數據處理、文本識別、有時序性的數組處理等更復雜的項目場景。伴隨著神經網絡的逐漸發展與進步，流量預測模型也不斷更新與發展。文獻[9]針對IP承載網核心網絡的流量變動問題，搭建人工神經網絡模型，并根據預測所得值對IP承載網核心資源進行更合理的分配，提高網絡效率。此外，在數據預測成功后的光網絡資源分配方面，有研究人員采用蒙特卡洛樹搜索的辦法實現光網絡彈性數據分配的功能，使網絡短時間內自適應變化。但是目前提出的各種方法，在IP承載網負載增加時成本增加迅速，資源消耗也迅速增多[9-10]。

隨著機器學習和通信網絡流量預測技術的緊密結合，光網絡也與計算機技術聯系得越來越緊密，令光網絡有機會越來越智能，越來越自動化，為光網絡自我優化提供了可能。目前，已有的光網絡與計算機技術結合成功的案例包括設備異常檢測和物理層故障檢測等[11-12]。4G/5G無線接入網技術也在不斷發展，并且需要采用虛擬化技術科學分配網絡負載資源，文獻[13-15]考慮基于IP承載網的多業務綜合通信。總之，目前的4G/5G網絡面向大規模接入，更需要科學地運用網絡負載分配和及時準確的流量預測技術。因此，本文以VoLTE業務在IP承載網的流量為研究對象，進行業務預測模型建模與分析，利用人工智能方法考慮流量數據時間上的相關性問題，從而實現對IP承載網流量的預測，進一步降低網絡擁塞并提升服務質量。

1 基于VoLTE的IP承載網網絡模型

采用深度學習技術與流量預測技術相結合的方法，通過建立相應的BP-ANN模型，實現對未來時間的流量預測，并判斷是否到達潮汐遷移時段。需要獲取在潮汐現象較強的網絡模型中各個用戶節點的網絡流量數據。目前，互聯網上關于城市的網絡流量數據相對較少，流傳較廣的是2015年意大利米蘭市于米蘭電信大賽上公布的米蘭市及附近幾個月的各種業務以及網絡流量數據，但是該數據更注重網絡數據各地區之間的相關性，對于城市不同地區的流量變化反映得不明確，因此本文擬建立反映潮汐現象的IP承載網拓撲模型，采集各個節點的流量數據。

在城市中，一般工作區相對較為集中，而住宅區可能相對更加分散，并且占據的節點更多，峰值的業務量更大。為了模擬IP承載網光網絡各個節點的流量和負載情況，要符合之前所說的要求。基于此，將IP承載網的光層抽象為如圖1所示的拓撲模型。由圖1可以看出，1，2，3，4這4個節點作為商業區的用戶節點，而9，10，11，12，13，14這6個節點作為住宅區的用戶節點，這樣滿足之前的要求，剩余的節點作為整個鏈路中剩余地段的用戶節點。

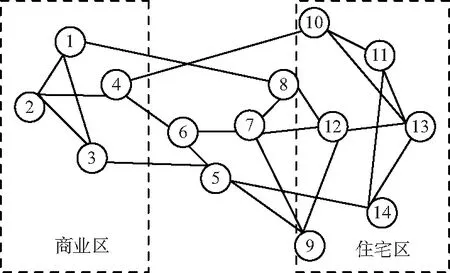
圖1 IP承載網分區域的拓撲模型結構Fig.1 Topology model structure of IP Network

利用NS2進行IP承載網分地區業務流量的仿真處理，各個節點之間采用光纖直連的方式。由于承載網中網絡器件存在噪聲會影響信道鏈路，在鏈路上添加高斯白噪聲來模擬器件噪聲。在仿真中，各個節點發生業務請求要符合泊松分布，同時，整個模型在任意時刻，請求發生的概率是隨機的，但不是均勻的。根據IP承載網流量的潮汐現象，在一段時間內按照白天的情況設置商業區節點的請求概率為住宅區的節點發送概率的2倍，在其余時間按照夜晚處理，二者發送概率相反。此外，系統中的業務傳輸也按照IP承載網特點，依據最短路徑和首次命中算法設置網絡傳輸路徑和資源分配方法。在采集數據時，規定每4 min采集一次數據，一共統計2 h，采集各個節點與鏈路上的流量數據。之后，對流量數據按照數據的最大值進行歸一化處理，獲得各個鏈路和節點的負載情況。針對流量數據的自相關性，將同一時間段的流量數據放在同一樣本中。最終，將采集到的時間信息和2 h內流量的歸一化數據作為最終得到的數據樣本進行分析。

2 基于深度學習的流量預測模型

針對本文提到的IP承載網潮汐流量特點，在分析之前常用的線性回歸法對流量預測的問題和局限性的基礎上，主要研究目前主要流量預測方法的適應性，并提出最優的IP承載網流量預測方法，構建準確率能達到85%以上的流量預測模型。

2.1 傳統時間序列的預測方法

一般在流量預測中常采用傳統時間序列的預測方法。傳統方法一般采用流量數據的回歸性來進行預測，但是IP承載網流量還受到地理位置和時間因素的影響，也就是說傳統方法的考慮是不夠全面的，所以基于深度學習的方法是更好的選擇。先介紹線性回歸和自回歸移動平均模型2種方法[16-17]。

2.1.1 線性回歸模型

(1)

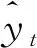
(2)

也就是說在有2個影響因素的情況下，可以記觀測值為：

{(yt，x1，x2，t)}，

(3)

2.1.2 自回歸移動平均模型

(4)

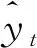
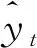
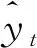
相對于這些傳統的基于時間序列進行流量預測的方式，采用ANN等神經網絡對流量進行預測會更加靈活，應用范圍也會更廣。在設置神經網絡時，只需要改變隱藏層節點數目和相應的偏置與權重值就可以模擬任意一個連續的函數，對于未來進行較好的預測。神經網絡不僅僅可以處理數值序列，也可以對圖片文字等進行識別。此外，針對數組的自相關性，采用LSTM等循環神經網絡也會有很好的效果。所以本文選擇利用神經網絡預測流量數據。

2.2 基于BP-ANN網絡的數據預測方法

ANN網絡與之前介紹的線性預測算法不同，屬于非線性統計性模型，它模擬了人腦神經元的網絡結構，可以實現相對復雜數據的存儲和處理功能。ANN網絡具有逐層的結構，由多層的神經元逐個逐層相連。各層之間相互映射，通過各個層上節點的連接實現數據的并行處理。與線性預測不同，ANN網絡的映射是非線性結構的，適合處理較復雜的數據和算法，并能夠通過訓練來符合系統要求，提高預測準確率。

ANN網絡有很優秀的學習能力，所以可以獲得較為真實的預測值，得到數值合理的真實系統。同時，這樣做的好處是網絡無需知道系統的具體信息，只需要知道系統的輸入值，根據設定的具體模型以及隱藏層結構，最終獲得輸出值。所以ANN網絡一般會用于解決模式識別等較為復雜的問題。在設計BP神經網絡時，最多的情況是采用3層神經網絡，也就是隱藏層只有1層的情況。在考慮3層網絡的情況下，對于輸入數據也有一定要求，因為有些時間采集的數據由于某種情況可能會存在數據的跨度大，數據收斂性差等情況，最終網絡的訓練時間就會很長，并且最終結果可能不會收斂。在網絡訓練之前，需要對數據進行預處理，同時為了使無論大或小的數據對網絡訓練的影響相同，需要將數據歸一化，使數據的均值減小。所以就需要把數據最終歸一化為(0，1)的數值或者(-1，+1)的數值。同時，還要考慮網絡的學習速率，這個數據是為了反映在訓練過程中每次的迭代步長等。

為了提高準確率，減小算法的誤差，還需要反向對數據進行處理，基于此，本文提出BP模型，用于計算ANN網絡中各級的權重。該算法通過逆向的誤差傳播，反向訓練其中的隱藏層和輸入層的神經元，借由其擁有的自我學習、自我調整能力實現獲得各層的偏重，最終使輸出迫近期望。一般的BP神經網絡模型如圖2所示。由圖2可以看出，分為輸入層、輸出層和隱藏層各神經元節點。輸入層和輸出層的數量都為1，而隱藏層有可能是1層，也有可能更多。

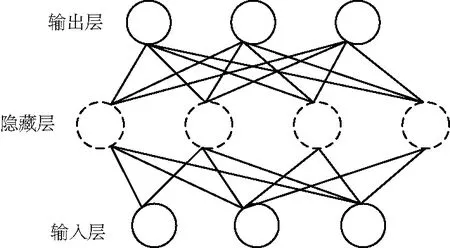
圖2 BP神經網絡模型Fig.2 Model of BP neural network

在BP神經網絡中，除了計算加權求和，激活函數f(t)也十分重要。BP神經網絡是非線性的，所以需要有一個非線性的激活函數來給它提供一個非線性的變換。常用的激活函數有Sigmoid函數和ReLu函數，它們是2種最基本的激活函數。

Sigmoid函數圖像如圖3所示，

圖3 Sigmoid函數圖像Fig.3 Function of Sigmoid

Sigmoid函數為：

(5)

其取值范圍為0～1，便于處理分類問題，但是在考慮反向傳播算法時，易發生梯度消失。

ReLu函數如圖4所示。

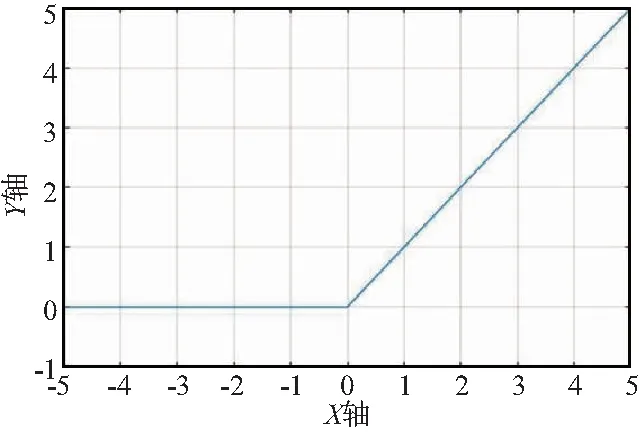
圖4 ReLu函數Fig.4 Function of ReLu

ReLu函數為：

φ(x)=max(0，x)，

(6)

其特點是結構簡單、收斂快，但是在處理一些連續的負數時，會對數據有激活現象。BP算法最重要的2個特點就是數據在向前傳播，同時誤差在進行反向傳播。

前向傳播的流程是數據通過輸入層進入網絡，通過隱藏層的處理，最后傳播到輸出層，獲得預測數據。對于只有一個隱藏層的網絡，即單隱藏層網絡，零輸入層數值為xi，隱藏層數據為cj，輸出層數據為yk，最終輸出的期望為qk，此外，各層的數據權重和偏置分別為wij，pjk，θj和bk，那么：

cj=f(∑wijxi-θi)，

(7)

yk=f(∑pjkcj-bk)，

(8)

這樣就根據輸入層的數據獲得了最終的數據。

對于反向傳遞，誤差的流經路徑與正向傳播正好相反，誤差通過反向傳播修正各級的權重。一般輸出層的誤差都會用均方值來評判：

(9)

經過多次計算，進行數次正向和反向傳播，使全局誤差收斂至極小值即可。歸結起來，BP神經網絡的訓練步驟主要為：

① 初始化網絡數據，設定網絡的初始參數；

② 計算輸出層的輸出；

③ 獲得在特定點的數據均方誤差；

④ 采用梯度下降的方法獲得更好的權重值和偏置；

⑤ 更新閾值；

⑥判定均方誤差是否達到特定值的要求，選擇結束迭代還是繼續訓練。

2.3 BP-ANN網絡模型參數設置與訓練方法

需要對IP承載網流量進行預測，而承載網的流量數據已經被處理為一個數據包，再通過BP-ANN[18]網絡模型以及LSTM網絡模型進行學習和預測。建立模型的目的是通過輸入一段時間的歷史網絡流量數據以及時間數據，預測未來某時刻的網絡流量數據。此外，還可以判斷某一時刻網絡是否進入潮汐遷移時段，更好地為IP承載網用戶提供高質量網絡服務。在預測結果中分為已經進入和未進入遷移時段，所以是一個典型的神經網絡的二分類問題。

在數據采集和處理過程中，還需要注意的是注意力機制，也就是要將數據處理以獲得最終適合網絡輸入的數據，對于目前的BP-ANN網絡和LSTM網絡都有一定的必要性，一般會采用Seq2seq模型來對數據進行處理。Seq2seq是一種編碼解碼器的結構，其輸入和輸出都是一種數據序列。在模型中的編碼器可以將輸入序列轉化為固定長度的中間序列，也稱為隱向量，這個中間序列會影響最終的輸出序列和預測結果。在解碼器端，模型會根據當前時刻隱向量的數據和之前時刻的模型輸出獲得當前時刻最終的模型輸出，然后再將序列轉化為需要長度的序列。但是需要注意的是Seq2seq模型有很大的缺點，在這個模型中，不同的值都有相同的數值權重，但是在一些實際案例中，比如本文的流量預測環境中，當前時刻的網絡流量應該是與臨近時刻的流量數據相關性比和較遠時刻的相關性要弱，所以序列的不同輸入數據權重應該有所區分。所以處理數據構建神經網絡必須要采用注意力機制。注意力機制中，主要采用的是Global Attention機制和Local Attention機制。首先，獲得所有編碼器時刻的隱藏層狀態輸出，再得到某時刻的解碼器的隱藏層的狀態輸出；然后，利用平分函數，也就是attn(htarget)得到某個時刻的時間對應的權重并進行歸一化，得到編碼器的輸出進行權重平均；最后，獲得最終的輸出概率。目前一般采用固定的函數來計算序列的權重和注意力數值：

(10)

式中，htarget是最終獲得序列的某時刻狀態；hi是此時刻的隱向量的值。根據匹配程度獲得其權重值，匹配度越高值越大，最終再將其歸一化，獲得方便計算的0～1的值。因此，設計了如圖5所示的BP-ANN神經網絡結構模型來進行IP承載網流量數據預測。

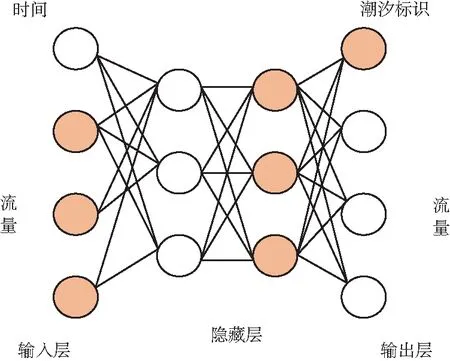
圖5 潮汐流量預測BP神經網絡模型Fig.5 BP neural network model for tidal traffic prediction

對于這個網絡的輸入，考慮為當前的2 h內每4 min采集的共15組數據以及時間數據，所以輸入層共31個節點。而輸出層也需要16個節點，包括未來1 h內的15次網絡流量數據以及判斷是否到達潮汐遷移時段。此外需要注意的是，為了判斷是否到達潮汐遷移時段，需要引入潮汐標識位，該輸出為1表示即將到達潮汐遷移時段；如果輸出為0則表示還未到達潮汐遷移時段。這是一個深度學習網絡中的分類問題。而流量預測問題則是一個回歸問題[19]。

對于隱藏層的層數以及每層上的節點數目，可以根據Kolmogorov公式來選取。Kolmogorov公式是一個經驗公式，可以為隱藏層提供一個范圍，然后可以在訓練過程中來選取最優的隱藏層數據。

在深度學習不斷發展的過程中，學者們給出了許多用于確定隱藏層結構的方法，其中最具代表性的就是經驗公式Kolmogorov公式[20]。Kolmogorov公式表明，對于僅有3層的簡單神經網絡，隱藏層節點數目h一般可以表示為：

(11)

式中，m為輸入層中神經元節點的數目；n為輸出層神經元節點的數目；a為一個范圍為1～10的調節系數，可能取到其中的任意值。在本文中，輸入層有31個節點，輸出層中有16個神經元節點，根據經驗公式可得當僅有一層隱藏層時，隱藏層的神經元的數目取值范圍在7～16之間。為了讓學習過程相對簡便，可以先令隱藏層神經元節點數為7，減小初始的計算量。經過相關研究論證，一旦隱藏層節點數目增多，BP-ANN網絡的學習效率將會不斷降低，所以要盡量減少隱藏層神經元節點的數目。

在訓練的過程中，會通過學習，預測30 d的網絡流量數據，然后再根據實際值進行驗證。總共統計30 d，每天會得到24組數據，一共得到720組數據，按照8∶1的比例，選取640組進行模型的訓練，利用剩余的80組數據來驗證該模型的分類能力和回歸[30]能力。

3 預測結果與數據分析

根據本文設計的BP-ANN網絡進行網絡流量數據預測，需要在計算機中搭建深度學習的平臺。本文中運用Tensorflow學習框架，利用Tensorflow來搭建上述的BP-ANN網絡，并進行數據集的訓練與學習。利用Tensorflow得到本模型訓練中loss值的變化如圖6所示。隨著訓練與迭代的次數逐漸增大，模型的loss值逐漸減小至收斂裝填，模型也逐漸穩定。

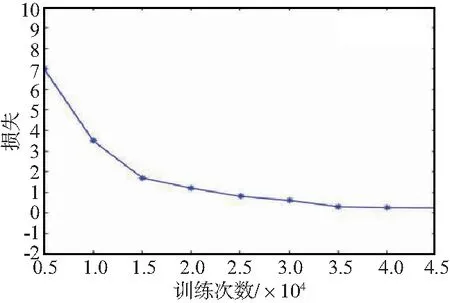
圖6 Tensorflow中損失隨訓練次數變化趨勢Fig.6 Variation trend of loss with training times in Tensorflow

可以看出，在訓練中，迭代次數會影響本算法的準確性和預測結果。為了明確本模型的可用性，需要對其性能進行評價。可以采用平均絕對誤差(MAE)來衡量本模型性能。MAE的計算表達式為：

(12)

該值通過計算絕對值之和，來衡量模型的預測值對于真實值的偏差。平均絕對誤差與訓練次數的變化趨勢如圖7所示。由圖7可以看出，MAE隨著訓練次數不斷增大，而平均誤差緩緩減小，預測值越來越接近真實值，也就是說，模型能夠對IP承載網的流量數據進行較為準確的預測。

圖7 平均絕對誤差與訓練次數的變化趨勢Fig.7 Variation trend of average absolute error with training times

預測潮汐遷移時段的準確率隨訓練次數變化的趨勢如圖8所示。由圖8可以看出，對于模型的分類能力，也就是模型能夠準確預測潮汐遷移時段的能力，訓練次數越大、迭代次數越多，模型準確率越高，最終趨向于90%。

圖8 預測潮汐遷移時段的準確率隨訓練次數變化的趨勢Fig.8 Variation trend of accuracy of tidal migration period prediction with training times

由于隱藏層的神經元節點數目在7～16，需要對節點數對于MAE的影響進行評估。可以預見，隨著隱藏層神經元節點數目增加，完成訓練的時間會不斷增大。MAE隨著隱藏層變化的數值關系如圖9所示。可以看出，當節點數少時，MAE相對較大，而當神經元節點數不斷增加，MAE值的變化也逐漸趨于平緩。

圖9 MAE隨著隱藏層變化的數值關系Fig.9 Numerical relationship between MAE and hidden layer

對于模型的分類能力與隱藏層節點數的關系的判斷，引入預測準確率的概念。預測的準確率反映的是模型對所有樣本的判斷能力，表達式如下：

(13)

式中，TP為實際到達預測對的次數；FP為實際未到達預測錯的次數；TN為實際到達預測錯的次數；FN為實際未到達預測對的次數。

預定進行10 000次訓練，然后改變隱藏層神經元節點的數目，獲得二分類模型的準確率與隱藏層節點數的關系如圖10所示。可以看出，模型的分類能力整體相對較好，與節點數基本無關。

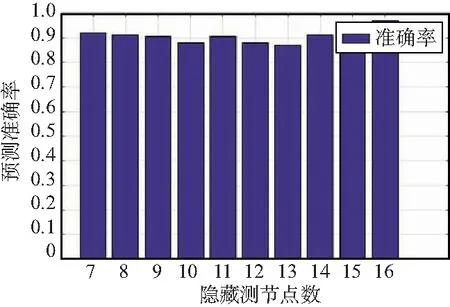
圖10 二分類模型的準確率與隱藏層節點數的關系Fig.10 Relationship between accuracy of binary classification model and the number of hidden nodes

按照31-15-16的結構構建BP-ANN神經網絡，設置迭代次數為100 000次，對模型進行預測，最終得到二分類模型的準確率與隱藏層節點數的關系如圖11所示。可以看出，模型預測能力相對較好，并且對于潮汐遷移時段的預測能力也相對較好，較好地預測了在18～19時會有IP承載網流量數據進行大幅度遷移，具備較好的預測性能。

圖11 BP-ANN網絡預測潮汐遷移標識出現隨時間的準確率Fig.11 Accuracy of BP-ANN network in predicting the occurrence of tidal migration markers with time

在IP承載網的資源重新分配和業務重構過程中，首先，要收集一段時間的網絡某些區域的網絡流量數據，通過已經建立的BP-ANN網絡利用采集到的數據進行處理后學習，再配置不同的權重以及偏置，預測未來某段時間的網絡流量數據；其次，需要不停地采集數據，對不同時刻的流量數據進行動態處理，不斷地獲得未來時刻的預測流量數據；然后，還要利用網絡的分類能力來判斷網絡是否達到潮汐遷移時段，如果達到了遷移時段，為了應對潮汐遷移現象，需要對業務進行重組，對信道網絡環境中的業務進行分類，根據其占用的帶寬以及持續時長和優先級進行歸類，將其按照權重歸入待處理業務中；最后，再為其動態的分配各個業務占用的頻帶資源等，就可以盡可能提高網絡的利用率。

4 結束語

分析常用的線性回歸法對流量預測的問題和局限性，采用基于深度學習的BP-ANN算法討論了基于VoLTE業務IP承載網的流量的預測問題，并驗證了模型的準確率和可靠性。首先利用BP-ANN神經網絡以對IP承載網流量進行預測以獲取某地區未來一段時間的網絡流量；然后，針對流量的未來變化以及其潮汐現象對網絡設備和配置進行動態調整，以提高網絡的利用率，同時，針對IP承載網流量的潮汐現象，在注意力機制的前提下通過設置合適的相關參數創建合適的BP-ANN神經網絡，并考慮流量數據在時間上的相關性，實現對IP承載網流量的預測。仿真結果表明，通過尋找預測模型的合適迭代次數，不斷減小模型的流量預測的誤差，可以使流量預測準確率基本達到85%以上，可以為現有IP承載網QoS部署策略進行優化提供有效的解決方案。