基于分形維數的密級配瀝青混凝土設計指標預估

（交通運輸部科學研究院，北京 100029）

0 引言

瀝青混凝土配合比設計是瀝青路面設計及施工過程中的重要環節，包括目標配合比設計、生產配合比設計及生產配合比驗證等階段，主要涉及礦料級配及油石比等參數的確定，在整個配合比設計過程中，施工礦料顆粒組成和瀝青用量是決定瀝青混凝土結構特性及路用性能表現的關鍵因素。用于瀝青混凝土中的礦料具有顆粒破碎不規則、粒度分布非線性不連續及排布空間隨機的特性，目前常采用級配曲線表征礦料顆粒特性，而直接采用級配參數對混凝土性能進行預估時，因影響不同級配類型瀝青混凝土性能的礦料關鍵控制篩孔不同且有多個，建立簡單明確的擬合關系較為困難。因此，如何基于礦料級配特性實現混凝土關鍵設計參數及路用性能的預估，即構建瀝青混凝土原材料參數與其設計指標之間相關關系，對簡化瀝青混凝土配合比設計過程具有重要意義。

分形理論可以定量描述幾何形體的復雜程度及空間填充能力[1]，適用于表征復雜的礦料粒度分布情況。截至目前，已有學者采用分形理論對瀝青混凝土礦料特性與混合料性能的關系展開研究。20 世紀90 年代初，謝和平[2]便開始利用分形理論研究巖石的破壞狀況。其后，高峰等[3-4]擬用分形維數表征巖塊破碎程度，研究表明破碎后的巖塊度呈現相應的分形特征，可用分形維數作為表征巖石破碎程度的指標；李曉軍等[5]運用分形理論對瀝青混合料破碎過程進行了動態識別研究；李曉燕等[6]通過分析粗集料軸向系數、分形維數等6 個參數，對粗集料形態特征變化的敏感性進行研究，并結合車轍試驗和貫入剪切試驗，發現分形維數是表征粗集料形態特征的最優指標；楊瑞華等[7]應用分形理論研究行業規范推薦的密級配瀝青混凝土礦料級配限值曲線，發現礦料級配具有分形特性；張飛[8]通過研究不同骨架類型的級配，提出兩段分形評價；Li 等[9]提出采用分形維數評價集料的形狀特征。分形維數也逐漸被許多研究者用作描述和評價礦料顆粒形態特征的指標[10]。這些研究表明，分形維數可作為量化表征瀝青混合料復雜程度的指標，一定程度上能簡化不同瀝青混合料之間復雜性的比較。在對礦料分形以及與瀝青混合料性能相關性的研究方面，顏強等[11]研究得出分形維數可作為斷面空隙復雜程度的評價指標，分形維數與瀝青混合料性能具有一定相關性；Hu等[12]研究發現，集料分形維數對混合料內部空隙分布具有明顯的影響，且具有正相關關系；陳國民等[13-14]研究發現，瀝青混合料的代表級配分形維數與其結構類型相關，其動穩定度與分形維數線性相關，且集料表面紋理曲線分形特性粗糙度越高，瀝青混合料的高低溫性能和水穩性能越好；李波等[15]研究發現，SMA-16 的體積指標與分形維數具有相關關系；張金輝等[16]研究得出，連續級配瀝青混合料集料分維對瀝青混合料的體積指標和使用性能均有較大的影響；姚形傲等[17]研究發現，隨著細集料的形貌特征分維增大，混合料極限彎拉應變與凍融劈裂強度比呈現先增后減的趨勢，但混合料的高溫穩定性變化不明顯；楊瑞華、崔通等[18-19]研究發現，規范推薦中粒式瀝青混凝土礦料級配曲線的分形特征與部分路用性能相關性較好。上述研究都表明，瀝青混凝土礦料的分形與瀝青混合料性能間有較強的相關性。

目前，將分形理論用于礦料級配與混凝土路用性能關系的研究多是在室內試驗條件下對規范推薦級配限值[20-21]的研究，且大多聚焦于礦料特征分形與混凝土部分性能的相關性上，規范限值間的差異表現顯著，故研究所得的相關性顯著。而工程實際中基本不采用級配限值，且生產工況和干擾因素等更復雜，因此工程實踐更關注利用的分形與性能的相關性指導混凝土設計。鑒于此，本文基于多條高速公路密級配瀝青混凝土的應用情況，系統分析了工程用不同類型瀝青混凝土礦料的分形特性，明確常用密級配瀝青混凝土礦料分形維數及油石比分布情況，進一步基于AC-13 型及AC-20 型瀝青混凝土構建瀝青混凝土設計指標預估方程，以便為瀝青混凝土配合比設計過程優化提供參考。

1 礦料的分形維數

目前，瀝青混凝土采用的礦料主要來源于破碎的天然石料，其破碎過程表現出不規則性和復雜性，但石料在由大粒徑到小粒徑的破碎過程中的破碎機理是相同的，具有自相似性或尺度不變性，破碎顆粒和粒度分布均表現出分形特征[2]。具有分形特征的礦料顆粒重構混凝土空間結構的生成過程，可簡化理解為破碎的逆過程，其特征也表現為分形[22]。由此，分形理論既可描述礦料顆粒粒度分布，又可描述顆粒混合排布過程特征，即可將級配與混凝土結構統一表征，采用分形理論可以簡化礦料級配與混凝土性能的相關關系。

1.1 分形理論

分形理論是法國數學家Mandelbrot 在研究海岸線等典型復雜自然形態并總結以往分形領域純數學理論研究的基礎上創立的，是以歐氏幾何難描述的不規則、無特征長度的形態為研究對象[23-24]。對于大多數復雜的自然形態，其具有統計意義上的自相似，局部放大與整體具有相同的統計分布規律[25]。對于海岸線這類復雜形態，用一維測度即長度δ1量測時需N次覆蓋曲線[26]，則曲線長度為L(δ)=Nδ，當δ→0 時，N→∞,L→∞。而用二維測度即面積δ2量測時，得到曲線長度的測值為0。這表明，一維測度尺度（即維數）太小，而二維測度尺度太大，被測形態維數介于1和2之間，存在分數維。

推廣至海岸線等復雜形態，其整體X由N個將X縮小ε倍的相似圖形（類似打印機縮印的概念）構成，由此形成相似圖形數的函數N(ε)=εD，D即具有維數意義[25]，稱為分維。對于線段、正方形、立方體等整數維形態，既可用維數表征其形態特征（即一維、二維、三維等），也可用其維度下的測度表征其形態特征（即長度L、面積L2、體積L3）。對于測度復雜性難表述的分數維形態，維數表達替代測度并包含測度復雜性的信息，可表征局部填充整體過程中的傳遞關系和具有的復雜性特征。一般分形維數D可采用公式（1）進行描述：

1.2 級配礦料的分形維數

按分形理論，可認為級配礦料是不同粒徑形態混合為一整體，即總顆粒為整體，亦即最大篩孔rmax通過顆粒數為一整體（通過率100%），整體由縮小為1/ε的相似圖形構成，相似圖形為篩孔r的通過顆粒數，相似圖形數的函數為N(ε)=εD，其中ε=rmax/r，則關于篩孔r的通過顆粒數N(r)可表達為：

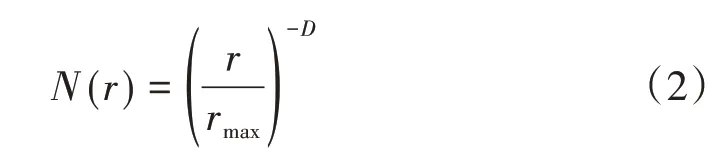
區間（r,r+dr）內的礦料顆粒數為：

因測量篩孔r的通過顆粒數非常復雜，實際礦料級配設計中采用篩孔r的通過顆粒的質量來表示礦料顆粒分布，即質量分布函數P（r）：

因礦料顆粒源于同種巖石破碎，可假設粒徑r的礦料顆粒密度均為ρ，則區間（r,r+dr）內，礦料顆粒質量可表達為式（5），質量分布函數可表達為式（6）：

式（4）～式（6）中：P（r）為礦料質量分布函數，表示礦料在篩孔r的通過率；M（r）為通過篩孔r的礦料顆粒質量，即不大于r粒徑的礦料質量（g）；M0為礦料總質量，即通過篩孔rmax的礦料顆粒質量；ρ為礦料顆粒密度（g/cm3）；k為基于特征尺寸的顆粒體積因子，為常數。

對式（6）進行積分，可得礦料顆粒質量分布函數P（r）與篩孔r的關聯簡式為：

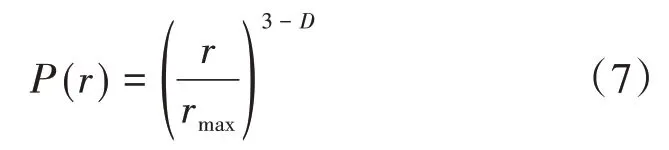
綜上，級配礦料的分形維數D如式（8）所示，可用于表征級配礦料的顆粒交互與顆粒填充混凝土整體的復雜性特征：

則3-D=，3-D即lgP（r）～lg（r/rmax）的最小二乘擬合直線的斜率。

1.3 密級配瀝青混凝土的礦料分形維數

為明確密級配瀝青混凝土的馬歇爾指標與原材料參數的關系，采集近兩年來多條高速公路不同路面結構層密級配瀝青混凝土原材料參數、配合比及馬歇爾設計指標。共采集數據200 余組，涉及上面層、中面層及下面層等結構層，涵蓋AC-13,AC-16,AC-20 及AC-25 多種級配類型，集料均采用玄武巖，填料為石灰巖質礦粉。在研究瀝青混凝土性能與礦料級配相關關系時，采用分形維數對混凝土級配進行表征，進一步研究混凝土相關性能與分形維數的關系，以避免直接采用級配參數進行擬合預估時出現控制變量過多的現象，有效優化預估過程。基于1.2 節中給出的計算方法，計算不同級配瀝青混凝土的礦料分形維數，計算結果如圖1 所示。對于不同類型的密級配瀝青混凝土均可采用同一分形維數對其級配情況進行表征，同時每一組混凝土均存在唯一分形維數。對于同一類型級配的瀝青混凝土，在進行工程應用時其礦料分形維數在一定范圍內波動，其中AC-20 型瀝青混凝土的礦料分形維數波動較明顯。

2 不同級配瀝青混凝土的礦料參數及油石比

在進行瀝青混凝土配合比設計時，主要是在確定礦料及瀝青類型基礎上進一步確定礦料級配及瀝青用量等參數。圖2 所示為不同級配密級配瀝青混凝土的礦料分形維數及油石比選用情況。

由圖2（a）可知，所調研的工程中，密級配瀝青混凝土的礦料分形維數基本在2.44～2.54 之間，擬合相關系數均在0.95 以上；不同級配瀝青混凝土的礦料分形維數存在差異，選用的瀝青混凝土礦料最大公稱粒徑較大時其分形維數相對較小。其中，AC-16 型瀝青混凝土的礦料分形維數相對較大，這主要與《公路瀝青路面施工技術規范》（JTG F40—2004）中推薦的混凝土的不同級配范圍有關。工程實踐中，在礦料級配選用時多以規范推薦級配中值為參考進行調整。本研究梳理實體工程中不同級配混凝土的礦料分形維數，發現與現有研究中變化趨勢一致[6]。

由圖2（b）可知，隨著密級配瀝青混凝土礦料最大公稱粒徑的增大，推薦油石比先增大后減小，AC-16 型瀝青混凝土的油石比較高，其均值在5.0%左右。結合不同級配混凝土分形維數變化規律可知，AC-16 型瀝青混凝土的分形維數較大，即該級配瀝青混凝土中細顆粒礦料含量相對較高，故在成型時瀝青用量也有所提升。

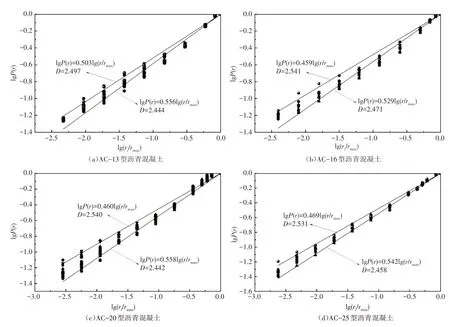
圖1 不同級配瀝青混凝土的礦料分形維數

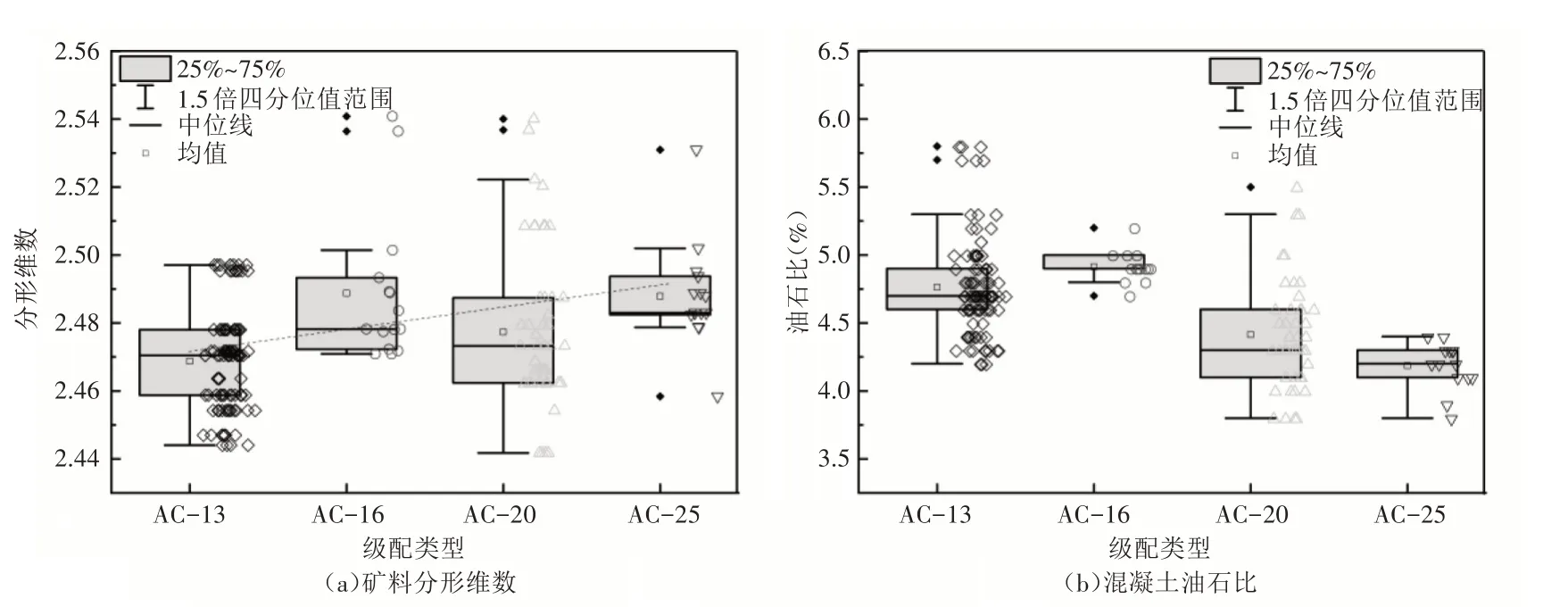
圖2 不同級配密級配瀝青混凝土原材料參數

3 密級配瀝青混凝土馬歇爾指標預估

目前，瀝青混凝土配合比設計主要以礦料級配及油石比為主，以馬歇爾設計指標進行控制，主要控制指標包括穩定度、空隙率、流值及飽和度等。礦料來源、級配、瀝青類型、瀝青用量等因素均會影響馬歇爾設計指標。在所調研的工程中，AC-13 及AC-20 型瀝青混凝土應用量較大。為減小各類型瀝青混凝土礦料產地和瀝青來源等因素的影響，在評估礦料分形維數及油石比對混凝土馬歇爾指標的影響時，主要以AC-13及AC-20 型瀝青混凝土為主，進一步形成基于分形維數與油石比的瀝青混凝土馬歇爾指標預估方程。

3.1 AC-13型瀝青混凝土馬歇爾指標預估

圖3（a）～圖3（c）所示依次為AC-13型瀝青混凝土的空隙率、穩定度、飽和度等指標與礦料分形維數及油石比的關系。對圖3 中馬歇爾設計指標與原材料參數進行多種曲面擬合，以期實現基于礦料分形維數及油石比的AC-13 型瀝青混凝土馬歇爾指標預估，擬合結果如表1、表2所示。在擬合過程中發現，流值與礦料分形維數及油石比均不存在顯著相關性，流值作為穩定度測試過程中瀝青混凝土發生破壞時的形變量，其影響因素不僅包括礦料分形維數、油石比等，瀝青型號等因素也會影響流值測試。

圖3 AC-13型瀝青混凝土馬歇爾設計指標變化規律

表1 AC-13型瀝青混凝土空隙率與原材料參數擬合預估方程對比

表2 AC-13型瀝青混凝土穩定度與原材料參數擬合預估方程對比

表3 AC-13型瀝青混凝土飽和度與原材料參數擬合預估方程對比

由圖3（a）可知，對于AC-13 型瀝青混凝土，其在標準條件下成型的瀝青混凝土空隙率受油石比及礦料分形維數共同影響。隨著油石比的增大，瀝青混凝土的空隙率逐漸下降，而礦料分形維數對混凝土空隙率的影響相對較小。表1 給出了AC-13 型瀝青混凝土礦料分形維數及油石比與空隙率的3 種擬合公式，R2為0.847～0.861，擬合優度較高；綜合相關系數及殘差項平方和，推薦采用表1 中序號3 的公式作為空隙率與礦料分形維數及油石比的預估關系式，即在明確礦料級配及油石比基礎上可參考該擬合公式對礦料空隙率進行預估。另外，根據擬合預估方程中油石比及礦料分形維數的系數比值可知，空隙率的主要影響因素為油石比。結合當前瀝青混凝土設計過程中常通過目標空隙率確定最佳油石比的現狀，在AC-13 型瀝青混凝土級配明確的基礎上可以基于預估方程反推最佳油石比。另外，亦可在配合比設計過程中利用該預估方程對推薦油石比進行驗證，確保試驗的準確性。

圖3（b）所示為AC-13型瀝青混凝土穩定度隨礦料分形維數及油石比的變化規律。同樣的，表2 中采用3 種公式對其相關性進行表述。其中序號3的公式相關系數明顯高于前兩個擬合公式，其擬合優度為0.691，相關性良好。綜合對比擬合公式中油石比及礦料分形維數的系數可知，礦料分形維數對混凝土穩定度的影響較大，油石比的影響相對較小。這表明，在AC-13 型瀝青混凝土配合比設計過程中，礦料級配是影響瀝青混凝土穩定度的重要因素。隨著礦料分形維數的增大，瀝青混凝土穩定度提高，在明確混凝土級配及油石比的基礎上，可采用推薦公式對瀝青混凝土的穩定度進行預估，初步確定其穩定度是否滿足設計要求。另外，考慮到混凝土穩定度與礦料分形維數相關性較好，在生產配合比驗證階段，可基于穩定度試驗反推混凝土分形維數，進一步對比生產配合比與設計配合比的差異。該思路能夠大幅減少現階段配合比驗證的繁瑣工序。

圖3（c）所示為AC-13 型瀝青混凝土的飽和度隨礦料分形維數及油石比的變化規律。表3 是基于不同擬合關系對其相關性進行分析，其中序號3 的公式相關系數較高，且其殘差平方和相對較小，故推薦該公式為擬合預估方程，其擬合優度為0.881。瀝青混凝土飽和度受油石比及礦料分形維數的影響較大，其中油石比對其影響顯著高于礦料分形維數，因此在明確目標飽和度的基礎上，可采用該預估方程反推瀝青混凝土的油石比，以減少試驗工作量。同樣，也可基于該預估方程檢驗試驗結果的準確性和可靠性。

3.2 AC-20型瀝青混凝土馬歇爾指標預估

圖4（a）～圖4（c）所示依次為AC-20型瀝青混凝土的空隙率、穩定度、飽和度等指標與礦料分形維數及油石比的關系。同樣對馬歇爾設計指標與原材料參數進行多種曲面擬合，擬合結果如表4～表6所示。

圖4 AC-20型瀝青混凝土馬歇爾設計指標變化規律

表4 AC-20型瀝青混凝土空隙率與原材料參數擬合預估方程對比

表5 AC-20型瀝青混凝土穩定度與原材料參數擬合預估方程對比

表6 AC-20型瀝青混凝土飽和度與原材料參數擬合預估方程對比

由圖4（a）可知，標準成型的AC-20 型瀝青混凝土的空隙率受油石比及礦料分形維數共同影響，其中油石比變化對瀝青混凝土的空隙率影響較大。表4 給出了AC-20 型瀝青混凝土的礦料分形維數及油石比與空隙率的擬合公式，3 種擬合公式的擬合優度為0.773～0.775，相關性良好。綜合對比后推薦采用表4 中序號3 的公式作為空隙率與礦料分形維數及油石比的預估關系式。相比AC-13 型瀝青混凝土，AC-20 型瀝青混凝土空隙率預估方程的相關系數較小，這表明礦料級配較大時，其空隙率受油石比及礦料分形維數的影響顯著程度有所下降，但整體相關性較好。因此，可在配合比設計過程中采用該預估方程對推薦油石比進行驗證，以提高試驗結果的可靠度。

圖4（b）所示為AC-20型瀝青混凝土的穩定度隨礦料分形維數及油石比的變化規律。表5 為構建的擬合預估方程式，其擬合優度為0.821～0.857。根據殘差平方和，推薦采用序號3 的公式作為預估方程式。相比AC-13 型瀝青混凝土，AC-20 型瀝青混凝土的穩定度擬合關系式相關性較高，這表明顆粒級配較粗的瀝青混凝土，其穩定度受礦料分形維數及油石比的影響較大，其中分形維數影響更顯著，即礦料級配越粗的混凝土在其配合比設計時，混凝土穩定度受礦料分形維數的影響越顯著。因此，對于AC-20 型瀝青混凝土，基于其穩定度測試結果反推混凝土分形維數的準確度更高，這樣也能更好地對比生產配合比與設計配合比的差異，簡化生產配合比驗證工序。

圖4（c）所示為AC-20 型瀝青混凝土的飽和度隨礦料分形維數及油石比的變化規律。表3 為構建的擬合預估方程，其中序號2 和3 的擬合公式的擬合優度相同，序號3 的公式殘差平方和相對較小，故推薦該公式作為擬合預估方程，其擬合優度為0.761。同理，在明確瀝青混凝土目標飽和度的基礎上，可采用該預估方程反推其油石比，以減少試驗工作量，結合表4 中推薦的擬合公式，提高預估結果的準確性。

4 結語

本文系統調研了200 余組密級配瀝青混凝土原材料參數及配合比設計參數，基于分形理論進行研究，推薦采用分形維數表征礦料級配特性，分析了工程常用不同級配瀝青混凝土礦料分形維數及油石比分布情況，并構建了瀝青混凝土設計指標預估方程，主要研究結論如下。

（1）不同密級配瀝青混凝土均可采用唯一分形維數對其級配特性進行表征，現有同一類型級配的瀝青混凝土的礦料分形維數在一定范圍內波動，礦料分形維數差異較小，工程采用的密級配瀝青混凝土的礦料分形維數基本在2.44～2.54 之間。隨著密級配瀝青混凝土礦料最大公稱粒徑的增大，推薦油石比先增大后減小，其中AC-16 型瀝青混凝土油石比較高，其均值約為5.0%。

（2）隨著油石比的增大，標準成型的密級配瀝青混凝土的空隙率及飽和度逐漸下降，而礦料分形維數對混凝土空隙率的影響相對較小。在明確瀝青混凝土級配的基礎上，可基于混凝土設計參數的預估方程反推最佳油石比，同時可在配合比設計過程中對推薦油石比進行驗證，以提升試驗精度。

（3）礦料分形維數對瀝青混凝土的穩定度影響較大，油石比的影響相對較小；隨著礦料分形維數增大，瀝青混凝土的穩定度呈增長趨勢；在生產配合比驗證階段，可基于穩定度試驗反推混凝土分形維數，并對比生產配合比與設計配合比的差異性，以減少現階段配合比驗證工序。

（4）構建了礦料分形維數、油石比與混凝土設計參數的預估關系式，擬合效果良好，可為混凝土配合比設計提供參考。在下一步研究中可增加工程用瀝青混凝土原材料參數，擴大路用性能調研范圍，進而基于海量數據構建原材料參數與混凝土路用性能的相關關系，進一步優化瀝青混凝土配合比設計。