二維聲全息的δ函數約束型射線波疊加法

張陽 向宇 石梓玉

摘? 要：利用波疊加法進行聲場重建是一個病態逆問題，極小的測量噪聲就可能導致重建結果完全失真.傳統方法是在重建過程中結合正則化手段以提高穩定性，但當系統矩陣由于全息模型配置不當而嚴重病態時，即便采用正則化手段也難以獲得令人滿意的結果.利用強指向性的狄拉克δ函數對二維Helmholtz方程的解集進行形狀約束，使得約束后的解集成為具有δ函數指向特性的射線波函數.利用該射線波函數替換傳統波函數后可使系統矩陣趨于主對角占優的良態形式，從而提高重構穩定性.通過數值仿真驗證了該射線波函數在二維聲場重建中的正確性及穩定性，同時給出了射線波函數疊加項數的一種選擇方法.結果表明：利用該射線波函數不僅可以有效地計算二維聲全息問題，而且降低了系統矩陣的條件數，提高了聲場重建穩定性.

關鍵詞：波疊加法;近場聲全息;狄拉克δ函數;重建穩定性

中圖分類號：TB52? ? ? ? ? ? ?DOI：10.16375/j.cnki.cn45-1395/t.2020.04.003

0? ? 引言

近場聲全息技術[1]（Near-field acoustic holography，NAH）是一種噪聲源識別、定位及聲場可視化的強有力工具.近幾十年來，眾多學者通過對近場聲全息進行深入研究后相繼提出了空間Fourier變換算法[2-3] （Spatial fourier transform，SFT）、邊界元算法[4-5]（Boundary element method，BEM）、波疊加法[6]（Wave superposition method，WSM）等全息算法，均取得了較好的效果.但是，這些方法也存在著相應的不足，例如：空間Fourier變換算法要求聲源面與全息采樣面必須具有規則的形狀，且在利用快速傅里葉變換算法（Fast fourier transform，FFT）進行重建計算時無法避免窗效應與卷繞誤差[7-8];邊界元法雖適用于任意形狀的聲源面及全息面，但在計算時存在復雜的奇異積分處理及特征波數處解的非唯一性問題[9]，嚴重影響了計算精度和效率.波疊加法由于將源強點布置在聲源面內部的一個虛擬邊界上，因此，不會出現邊界元法中的奇異積分處理，但仍存在著不足——即特征波數處聲場解的非唯一性及重建病態問題.針對非唯一性問題，國內外學者已經進行了大量研究，并相繼提出了復數形式的Burton-Miller型組合層勢法[10]、復數矢徑波疊加法[11]、附加源波疊加法[12]等，均取得了很好的效果.而對于重建病態問題，目前的方法一般是在求解過程中應用正則化以得到穩定的近似解[13-15].但常規的正則化方法僅是通過數學手段對病態方程組進行后期的數值處理，并沒有改善物理模型本身的不適定性，因此，若當模型配置不當而導致問題本身嚴重病態時，即使再結合正則化也難以得到令人滿意的近似解.針對該問題，參考文獻[16]從改善波疊加法物理模型本身的不適定性出發，提出了一種無需正則化就能穩定重建聲場的射線等效源法[16]，為改善基于波疊加法的聲場重構病態問題拓展了一條全新的思路.該射線等效源法是利用格林函數的各階導數替換傳統波疊加法積分核函數，以使積分方程在離散后得到的系統矩陣呈現主對角占優的良態形式，從而改善重構病態問題.但是格林函數在求導階數較高的情況下表達式將變得非常復雜，難以計算，且在二維情況下，格林函數的導數并不具備單一方向的指向性，因此，需另尋一種構造射線波函數的方法.

本文利用強指向性的狄拉克δ函數對二維Helmholtz方程的解集進行形狀約束，使得約束后的解集成為具有δ函數指向特性的射線波函數.由于無需對格林函數求導，因此，極大地提高了計算效率和穩定性.文中給出了該射線波函數的詳細推導過程和疊加項數的選擇方法，并利用二維脈動圓環和隨機點聲源對本文方法的正確性及穩定性進行了驗證.

1? ? 基于波疊加法的聲場重建算法[6]

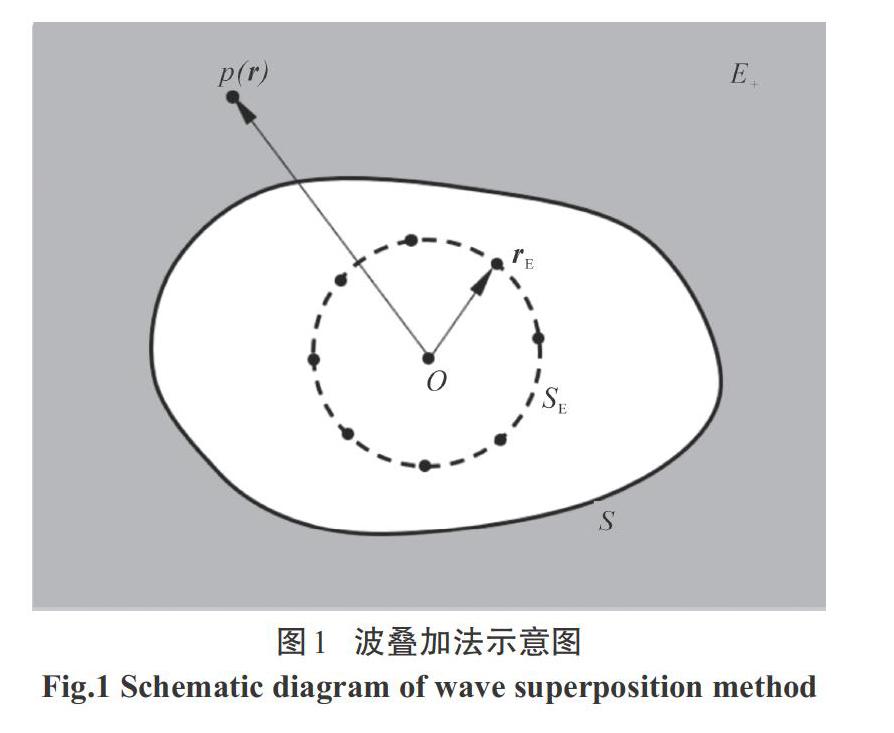
波疊加的基本思想為：振動體向外輻射的聲場可由置于其內部的所有虛擬等效源所產生的聲場疊加代替，而這些虛擬等效源強度可通過匹配聲源面或全息面的相關信息得到.如圖1所示，考慮一任意形狀的二維振動體，其中[S]為振動體邊界，[E+]為振動體外部輻射域.假設在振動體內部的虛擬邊界[SE]上布置等效源，則外域[E+]中任意場點[r]處聲壓可表示為：

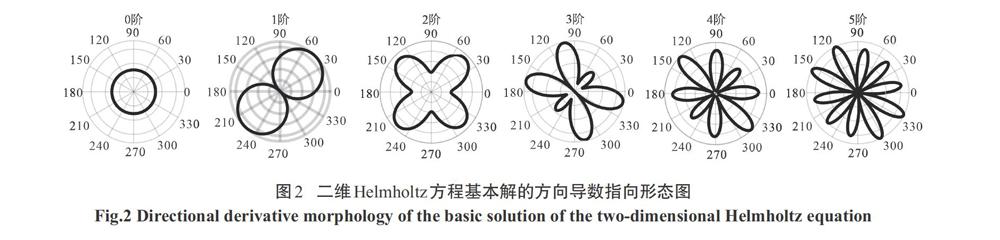
以上就是基于波疊加法的聲場重建算法.由于系統矩陣[GHE]通常是病態矩陣，因此，利用式（6）求解源強是一個病態逆問題.文獻[16]中對系統矩陣的病態性進行詳細分析后指出：由于傳統波疊加法采用的是球面形式的格林函數作為波函數，因此，將會導致系統矩陣由于列線性相關性過強而病態.為解決該問題，文獻[16]通過對三維Helmholtz方程的基本解（即自由場格林函數）求方向導數的方式構造了一種具有強指向性的射線波函數.利用該射線波函數替換傳統波疊加法的球面波函數后改善了系統矩陣的病態性，提高了重建穩定性.但在二維情況下，Helmholtz方程基本解的方向導數并不具備三維情況下的單一方向指向性，而是呈發散狀，如圖2所示，圖中求導方向為[1， 1].因此，需另行探索一種可適用于二維平面的射線波函數構造方法.

2? ? δ函數約束型射線波函數的構造

顯然，式（8）的解可作為波疊加法波函數，且通過匹配不同的展開項系數[An]，可使其具有任意形狀的波函數.換言之，若能夠匹配出適當的展開項系數[An]，就可以使式（8）成為具有單一方向指向性的射線波函數.本文的方法是利用具有指向性的狄拉克δ函數作為約束函數對式（8）進行形狀約束，由此匹配出相應的系數[An]，使得約束后的式（8）具備與輔助函數相同的指向性質.

狄拉克函數[δx-x0]是一個具有脈沖性質的廣義函數，它在[x=x0]點處具有無窮集中的指向性，而該指向性可以由其逼近序列[δnx-x0]體現，如圖3所示，圖中給出了狄拉克[δx-x0]函數的其中一個逼近序列：[πn11+n2（x-x0）2].

可以看到，隨著[n]的增大，逼近序列[δnx-x0]在[x=x0]點處越來越“尖”，即指向性越來越強，符合射線波函數的指向性要求.因此，可以考慮將[δx-x0]作為約束函數對式（8）進行形狀約束.

如圖4所示，假設第[i]個等效源點[rEi]與其對應主測點[rHi]的位置已確定，以該等效源的位置為原點設置一個與絕對坐標系平行的局部坐標系[（xi， yi）]，此時該等效源點[rEi]與其對應主測點[rHi]之間的距離為[rHi， Ei=rHi-rEi]，主測點[rHi]與局部坐標[xi]軸的夾角為[φxi， Hi].顯然，若該等效源[rEi]所輻射的是射線波，那么該射線波的主指向與局部坐標[xi]軸的夾角也必然是[φxi， Hi].假設使用δ函數對該波函數進行約束，那么該δ函數的形式為[δφ-φxi， Hi].這里[φ∈0， 2π]，表示將δ函數在該等效源（局部坐標原點）處沿周向展開，且在主指向角[φxi， Hi]處具有脈沖指向性.

假設δ函數[δφ]在圖4的局部坐標系[（xi， yi）]下可由式（8）的無窮疊加項展開，那么有：

由于波函數的指向特性只與角度有關，因此，在式（9）中已將式（8）中的變量[r]寫為常量[rHi， Ei]，表示在以等效源點[rEi]為原點，[rHi， Ei]為半徑的圓上計算聲壓幅值;[Ani]表示局部坐標系[（xi， yi）]下的展開項系數.值得注意的是，由于δ函數是沒有具體數學表達式的廣義函數，因此，式（9）表示當展開項系數為[Ani]時，式（9）右邊的無窮項疊加將成為與δ函數一樣的脈沖指向函數.由此容易推知，若取有限疊加項，式（9）的右邊就成為δ函數的一個逼近序列，并且該逼近序列滿足Helmholtz方程.

由圖5可以看到，隨著疊加項數[m]的增大，波函數在主指向角方向的指向性越來越強.若采用上述射線波函數替換傳統波疊加法中的球面波函數[Gr， rEi]，各等效源點所輻射的聲場如圖6所示.

由圖6可以看到，此時各等效源所輻射的聲場在其對應主測點處最大，而在其他非主測點處迅速衰減.因此，等效源與全息面間系統矩陣的主對角元素將比非主對角線元素大得多，系統矩陣呈現主對角占優的形式.等效源點與全息采樣點之間的系統矩陣[KHE]為（為便于計算，不妨令等效源點與全息采樣點數目一致）：

[KHE=KrH1， E1， φx1， H1， φx1， H1， rH1， E1KrH1， E2， φx2， H1， φx2， H2， rH2， E2…KrH1， EN， φxN， H1， φxN， HN， rHN， ENKrH2， E1， φx1， H2， φx1， H1， rH1， E1KrH2， E2， φx2， H2， φx2， H2， rH2， E2…KrH2， EN， φxN， H2， φxN， HN， rHN， EN??KrHN， E1， φx1， HN， φx1， H1， rH1， E1KrHN， E2， φx2， HN， φx2， H2， rH2， E2…KrHN， EN， φxN， HN， φxN， HN， rHN， EN]

其中：系統矩陣[KHE]的第[i]行、第[j]列的元素為：

[KHEij=KrHi， Ej， φxj， Hi， φxj， Hj， rHj， Ej=2π2πn=-m+mH2nkrHi， EjH2nkrHj， Ejein（φxj， Hi-φxj， Hj）]，[rHi， Ej=rHi-rEj]，[rHj， Ej=rHj-rEj]，[φxj， Hi]表示[rHi]與局部坐標[（xj， yj）]橫軸[xj]的夾角，[φxj， Hj]表示等效源[rEj]對應的主指向角，各變量見圖6.同理可得等效源與任意場點間的系統矩陣[KRE].

當利用系統矩陣[KHE]和[KRE]進行聲場重建時，式（5）—式（7）可寫為：

[PH=KHEQHE]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（15）

[QHE=K+HEPH]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（16）

[P=KREK+HEPH]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（17）

式（15）—式（17）即為基于本文提出的射線波函數的聲場重建公式.

3? ? 數值算例仿真與討論

3.1? ?二維脈動圓環聲場重建驗證

利用二維脈動圓環作為聲源驗證運用本文方法進行聲場重建的正確性.已知半徑為[rS]，周邊產生均勻徑向振速幅值為[v0]的脈動圓環在距離圓心[r]處所輻射聲壓的解析解為[20]：

為驗證本文方法在聲場重建計算中的正確性，在不添加噪聲的情況下進行聲場計算.選取射線波函數的疊加項數[m]分別為2、4、5、8、10、15，其余參數設置如下：聲源面半徑[rS=]1 m，等效源面半徑? ? [rE=]0.2 m，全息采樣面半徑[rH=]1.1 m.采用不同疊加項數計算得脈動圓環表面聲壓如圖7所示.

由圖7可以看到，利用本文方法計算所得的表面聲壓無論是實部還是虛部都能與解析聲壓相吻合，說明本文方法能夠正確地反演聲場.

為進一步探究聲場重建效果與疊加項數之間的關系，取疊加項數[m=0?30]，頻率[f=350 Hz]，并在不加噪聲與加噪聲（[SNR=30 dB]）的兩種情況下分別進行計算.為更加直觀地體現系統矩陣性態對于重建穩定性的影響，本文所有數值仿真均不使用任何正則化手段，直接使用Matlab中的“inv”函數對矩陣求逆.定義聲壓相對誤差[δsp]：

將疊加項數[m]的取值區間分為0～3、4～26、27～30三種情況分別討論圖8的結果.

1）當疊加項數為0～3時，無噪聲情況下的聲壓重建誤差均在[5%]以內，說明此時能夠正確地進行聲場重建計算.但在加噪聲的情況下，并不能很好地重建聲場.這是因為此時的射線波函數指向性不足、系統矩陣的病態性并未得到足夠的改善，放大了測量噪聲.

2）當疊加項數[m=4～26]時，無噪聲情況下的重建誤差都小于[5%]，加噪聲情況下的重建誤差也都控制在5%～10%之間.這說明在此區間內，原本病態的系統矩陣得到了改善，因此能夠穩定地進行聲場重建.

3）當疊加項數m=27～30時，隨著疊加項數的增大，其聲壓誤差也隨之變大.這是由于過大的疊加項數導致射線波函數的指向性過強，進而各虛擬等效源所輻射的能量在其主指向處過于集中，而在非主指向處衰減過快，由此導致了部分系統信息的缺失，因而無法很好地重建聲場.同時也發現，加噪聲與不加噪聲的兩條誤差曲線在27項后幾乎重合，這說明此時雖然已經不能很好地重建聲場，但噪聲并未對重建結果產生明顯影響.這意味著此時系統矩陣的病態性已經得到了改善，有效地抑制了噪聲對于重建結果的干擾.

由以上分析可知，射線波函數的疊加項數[m]須在合理的范圍內進行選擇.

3.2? ?輔助面法

可采用輔助面法[21]確定疊加項數[m].輔助面法的基本思想是：在全息采樣面與聲源面之間選取一輔助面[Γ]，通過比較輔助面上測量聲壓與重建聲壓相對誤差的最小值來確定合適的疊加項數.該問題可描述為：

3.3? ?隨機點聲源聲場重建驗證

由于實際結構聲源并無解析解可循，所以難以進行聲場重建驗證.但由惠更斯疊加原理可知，任意聲源皆可看作無數點源的集合.因此，可用隨機布置的一系列不同強度的點聲源考察本文方法在實際復雜聲場重建中的正確性及穩定性.

已知數量為[n]的點源在二維平面所輻射的聲場為：

式中：[σi]為第[i]個點源的強度系數;[gr， ri]為二維Green函數.在仿真計算中，取點源數量? ? ? [n=30]，并隨機分布于中心位于坐標原點、半徑為[1]的圓域內，點源強度隨機從[0?1]中選取.

該算例參數如下：節點數[N=70]，頻率? ? [f=]800 Hz，信噪比[SNR=40 dB]，等效源半徑[rE=]0.4 m，全息面半徑[rH=]1.1 m.輔助測量面為半徑[rΓ=]1.05 m的圓環.其中，疊加項數取值范圍[m=0?25]，重建觀測點數量為[50]，均勻分布在[-2， 1]到[2， 1]的線段上.

首先利用輔助面法計算不同疊加項數下的聲壓誤差，如圖9所示.由圖9可以看到，輔助面上的聲壓相對誤差在疊加項數[m=6～20]時大致相同，因此，為了提高計算效率，選取疊加項數[m=6].利用選出的疊加項數進行聲場重建計算，結果如圖10所示.可以看到，在傳統方法已無法得到穩定重建結果的情況下，本文方法仍可得到令人滿意的穩定計算結果.表1給出了傳遞矩陣[ΚHE]的條件數，可以看到，本文方法有效地降低了系統矩陣的條件數，明顯改善了系統矩陣的病態性.

4? ? 結論

基于將傳統球面波函數替換為強指向性射線波函數以改善系統矩陣病態性的思想，提出了一種構造射線波函數的新方法.該方法利用狄拉克δ函數對二維Helmholtz方程的解集進行形狀約束，得到了一系列具有δ函數指向特性的射線波函數.通過數值仿真驗證了該射線波函數在二維聲場重建中的正確性及穩定性，同時給出了射線波函數疊加項數的一種選擇方法.計算結果表明：本文方法不僅可以有效地計算二維聲全息問題，而且降低了系統矩陣的條件數，提高了聲場重建的穩定性.本文雖僅對二維情況進行了推導與探究，但其基本理論和方法可以方便地推廣到三維情況，因此，仍具有一定的研究價值.

參考文獻

[1]? ? ?WILLIAMS G E，MAYNARD J D. Holographic imaging without the wavelength resolution limit[J]. Physical Review? ? ? ?Letters，1980，45（7）：554-557.

[2]? ? ?WILLIAMS E G，MAYNARD J D，SKUDRZYK E. Sound source reconstructions using a microphone array[J].Journal of the Acoustical Society of America，1980，68（1）：340-344.

[3]? ? ?VERONESI W A，MAYNARD J D. Nearfield acoustic holography （NAH）-II-holographic reconstruction algorithms and computer implementation[J].Journal of the Acoustical Society of America，1987，81（5）： 1307-1322.

[4]? ? ?MAYNARD J D，WILLIAMS E G，LEE Y. Nearfield acoustic holography：I. Theory of generalized holography and the? development of NAH[J].Journal of the Acoustical Society of America，1985，78（4）： 1395-1413.

[5]? ? ?CUNEFARE K A，KOOPMANN G H，BROD K. A boundary element method for acoustic radiation valid for all wavenumbers[J].Journal of the Acoustical Society of America，1989，85（1）：39-48.

[6]? ? ?KOOPMANN G H，SONG L M，FAHNLINE J B. A method for computing acoustic fields based on the principle of wave superposition[J].Journal of the Acoustical Society of America，1989，86（6）：2433-2438.

[7]? ? ?FLEISCHER H，AXELRAD V. Restoring an acoustic source from pressure data using wiener filtering[J]. Acta Acustica? ? United with Acustica，1986，60（2）：172-175.

[8]? ? ?KWON H S，KIM Y H. Minimization of bias error due to windows in planar acoustic holography using a minimum error? ?window[J].Journal of the Acoustical Society of America，1995，98（4）：2104-2111.

[9]? ? ?CHAPPELL D J，HARRIS P J. A Burton–Miller inverse boundary element method for near-field acoustic holography[J].Journal of the Acoustical Society of America，2009，126（1）：149-157.

[10]? ?BENTHIEN W，SCHENCK A. Nonexistance and nonuniquness problems associated with integral equation methods in? ?acoustics[J]. Computers and Structures，1997，65（3）：295-305.

[11]? ?向宇，黃玉盈. 基于復數矢徑的波疊加法解聲輻射問題[J].固體力學學報，2004，25（1）：35-41.

[12]? ?夏雪寶，向陽. 基于附加源波疊加法的聲輻射計算研究[J].振動與沖擊，2015，34（1）：104-109，144.

[13]? ?TIKHONOV A N，ARSENIN Y V. Methods for solving ill-posed problems[M].Moscow：Nauka，1979.

[14]? ?WILLIAMS E G. Regularization methods for near-field acoustical holography[J].Journal of the Acoustical Society of America，2001，110（4）：1976-1988.

[15]? ?CHARDON G，DAUDET L，PEILLOT A，et al. Nearfield acoustic holography using sparsity and compressive sampling principles[J].Journal of the Acoustical Society of America，2012，132（3）： 1521-1534.

[16]? ?石梓玉，向宇，陸靜，等. 一種提高聲場重構穩定性的射線等效源法[J].廣西科技大學學報，2019，30（3）：1-7，21.

[17]? ?陳心昭，畢傳興.近場聲全息技術及其應用[M].北京：科學出版社，2013.

[18]? ?許伯熹. Helmholtz方程解的唯一延拓及逆源問題[D].上海：復旦大學，2014.

[19]? ?JEFFREYS H，JEFFREYS B. Methods of mathematical physics[M]. 3rd. Cambridge：Cambridge University Press，1999.

[20]? ?WU W T，OCHMANN M. Boundary element acoustics fundamentals and computer codes[J].Journal of the Acoustical? ? ? ? Society of America，2002，111（4）：1507-1508.

[21]? ?畢傳興.基于分布源邊界點法的近場聲全息理論與實驗研究[D].合肥：合肥工業大學，2004.