基于輸入整形方法的2 自由度機械臂運行過程振動抑制

張美艷，鄒懷武，王和慶，唐國安

（1.復旦大學 航空航天系，上海 200433；2.上海宇航系統工程研究所，上海 201109）

0 引言

機械臂因其靈活可變的運行形態，對于不同任務具有較強的適應能力，在空間技術方面有著廣泛的用途，如內置載荷釋放、目標星捕獲、空間垃圾回收、資源補給、艙外設備安裝和維修、空間站交會對接、支持航天員出艙活動等［1-4］。

由于空間應用領域對部件設備的自重指標都有較大的限制，面向在軌應用的機械臂強度和剛度設計裕度相對較低。然而，空間機械臂經常需要轉運質量、慣量較大的對象，小至航天器的有效載荷，大至衛星整體或艙體整器。機械臂的剛度低，而轉運對象的質量大，兩者結合后組合體的轉運應視為動力學過程，強度校核也應計入動態載荷。

動態載荷一部分是由變速運動加速度引起的，通過優化機械臂的行程（軌跡）可以克服或削弱，是機器人或機械臂動力學與控制研究的主要內容之一。

這方面的研究是從機械臂角度入手，較少考慮轉運對象的彈性特征，因此，不同的對象有可能規劃出相同的行程。動態載荷的另一部分是因為彈性振動引起的，與被轉運結構的慣性和彈性特性有關，相同行程的轉運過程也會產生不同的振動響應。這部分振動可考慮用輸入整形方法進行抑制。輸入整形方法是一種根據結構振動特性（包括固有頻率和模態阻尼）對外力函數進行整形，使得經過整形的外力函數激勵結構所產生的動態響應比原外力函數激勵下的響應更小［5-7］。

從Laplace 變換的角度觀察輸入形方法，其基本原理就是整形后外力函數所包含的零點恰好就是結構的激勵-響應傳遞函數的極點，理論上結構在這樣的外力函數作用下不會激起自由振動響應的。因此，當外力激勵停止后結構就不再有殘余振動。輸入整形方法在機械臂以及航天應用方面都有不少研究［8-12］。

由3 個連桿（其中第1 個連桿可視為航天器本體）、2 個關節的2 自由度機械臂是最簡單的機械臂構型。這種機械臂運動關系相對簡單，逆運動學可以采用解析方法求得封閉解。本文以此類型機械臂為例，用實驗方法驗證輸入整形方法對彈性體轉運過程的振動抑制效果，探討其在空間機械臂操控中的應用潛力和實施方案，并就相關數學和力學問題進行了梳理，例如闡述了整形器歸一化條件能使得整形后的速度函數具有總行程不變的特性。

1 機械臂(逆)運動學和輸入整形方法

1.1 2 自由度機械臂的運動學和逆運動學

驗證試驗使用的2 自由度機械臂，基本構型及參數如圖1 所示。機械臂原點位于o1點，雙臂長度分別為L1和L2。模擬衛星的重物通過彈性緩沖器安裝在末端o2點。2 自由度機械臂的末端只能限制在平面內運動，描述整個系統運動的自由度為2，后臂與水平軸的夾角θ1以及前臂相對于后臂的夾角θ2作為廣義坐標。

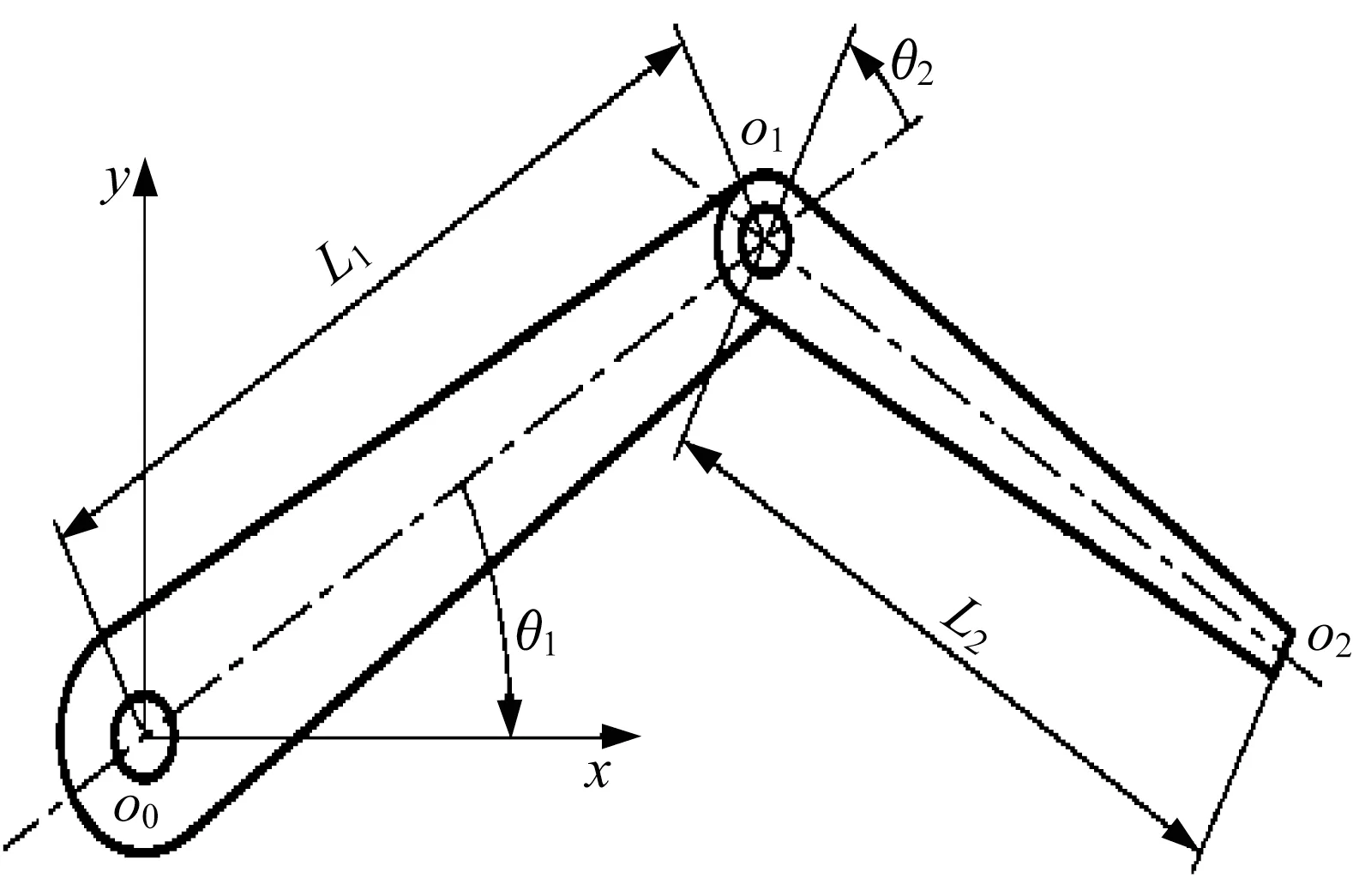
圖1 2 自由度機械臂示意圖Fig.1 Schematic diagram of the mechanical arm with two degrees of freedom

根據廣義坐標θ1、θ2（肩關節和肘關節的轉動角度）計算末端笛卡爾坐標(x，y)，稱為機械臂運動學。對于2 自由度機械臂，寫出如下笛卡爾坐標與廣義坐標的運動學關系：

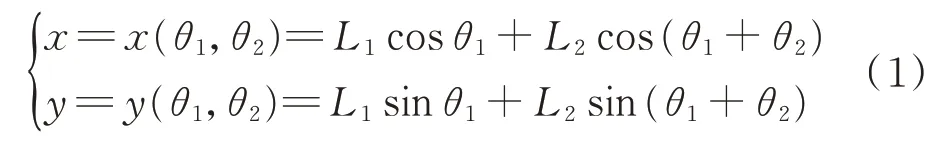
根據笛卡爾坐標(x，y)計算關節轉動角度θ1，θ2，稱為逆運動學。一般情況下，逆運動學并不是唯一的。

如圖2 所示，機械臂末端位于o2=(x，y)點。記o0與o2之間的距離為d，線段o0o2的極角為θ，后臂、前臂與線段o0o2的夾角分別為α、β。利用余弦定理可求得方程（1）的兩組解：

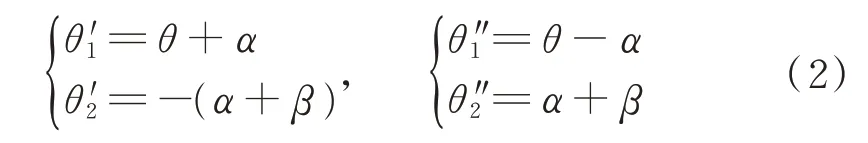
式中：

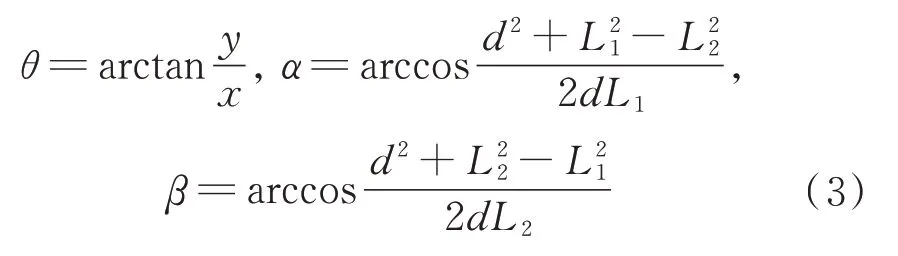
式（1）的逆運動學求解也可以采用數值求解方法，比如Newton 迭代法［13］。給定笛卡爾坐標(x*，y*)，估計一組廣義坐標的初值，Newton的迭代法格式為

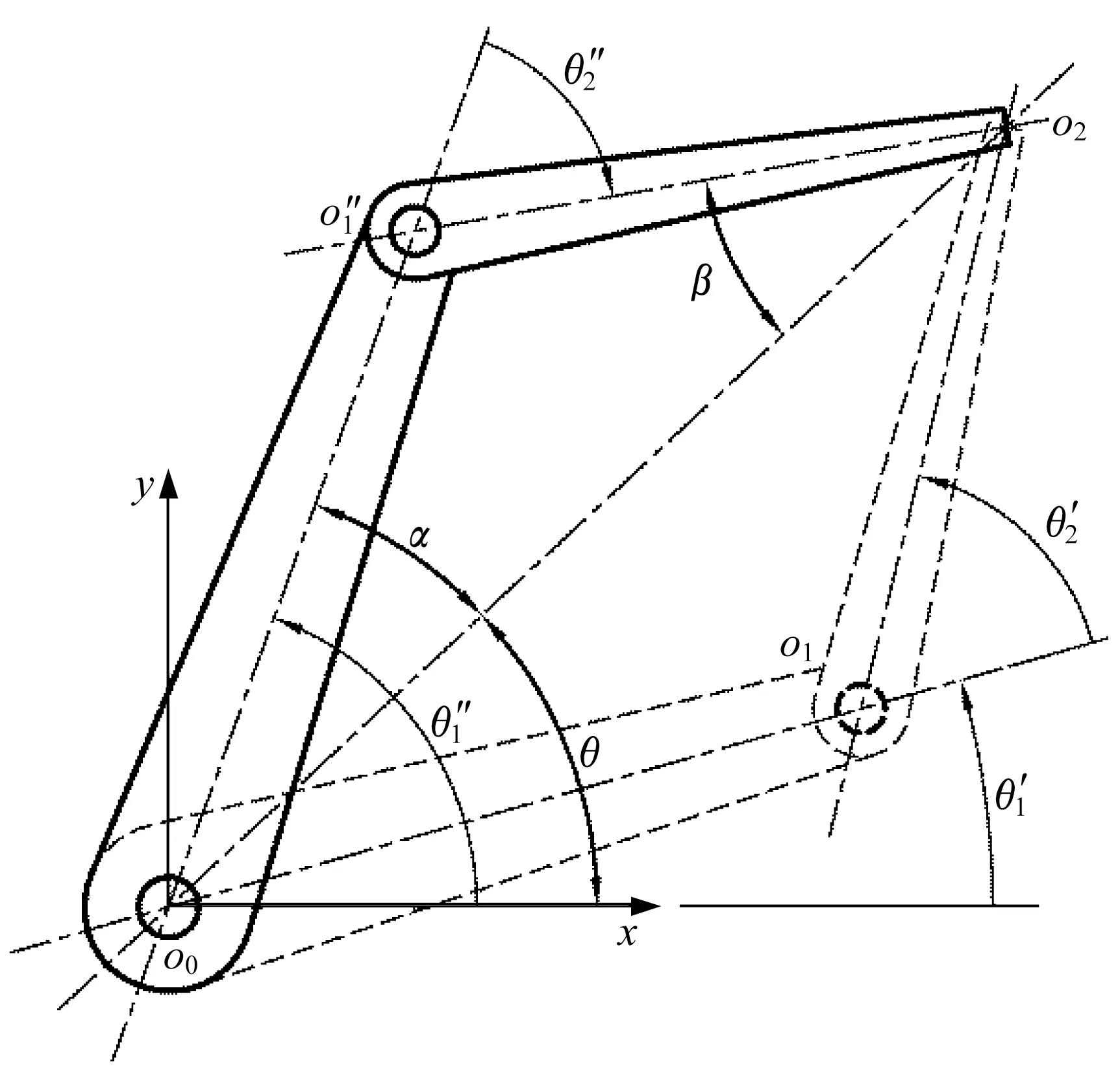
圖2 2 自由度機械臂逆運動學的多解性Fig.2 Multiple solutions for the inverse kinematics of the mechanical arm with two degrees of freedom

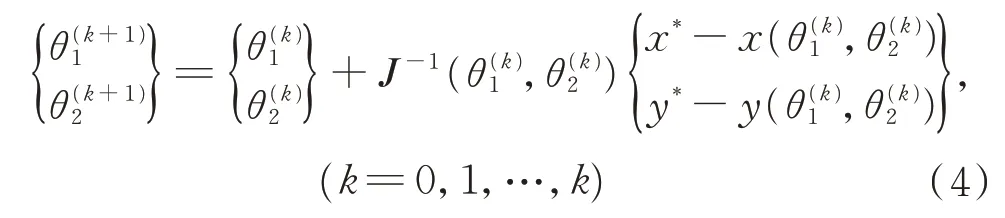
式中：Jacobi 矩陣

在迭代收斂的情況下有

行程設計要求在T時刻內，將機械臂末端從笛卡爾坐標為p0=(x0，y0)的起點移動到笛卡爾坐標為pn=(xn，yn)的終點上。常用的行程設計有笛卡爾坐標設計方法和關節轉角設計方法。

笛卡爾坐標行程設計法選擇直線運動實現機械臂末端從p0到pn的運動，期間經歷勻加速、勻速和勻減速3 段變速直線運動。在ti時刻（i=0，1，…，n），根據直線運動關系容易算出機械臂末端的位置pi，其中，ti=iT/n。然后再根據逆運動學，依次計算2 個關節的轉角θ1i和θ2i。

關節轉角行程設計方法相對簡單，2 個關節的轉角行程可以獨立設計。對于關節1，根據逆運動學計算得到起點和終點處的轉角θ10和θ1n，再對起始、停止時刻的速度和加速度予以適當的約束，例如令，于是就能確定一段以5 次多項式表示的關節1 的轉角函數θ1(t)。關節2轉角行程的設計方法完全相同。采用關節轉角設計的行程只有在起點和終點處的笛卡爾坐標是可控的，行程中的笛卡爾坐標只能由運動學式（1）計算，通用性不如采用笛卡爾坐標的行程設計方法。本文將要介紹的輸入整形驗證試驗將采用笛卡爾坐標設計的行程。

1.2 機械臂末端行程的輸入整形

作者將輸入整形方法應用于航天器在調姿、變軌過程中的柔性附件振動抑制［14-15］。所謂輸入整形器，就是由彈性結構m對固有頻率和模態阻尼所確定的2m個常數a1，a2，…，a2m以及一個延時量ΔT。施加在結構上的外力函數f(t)經過整形后新的形式為

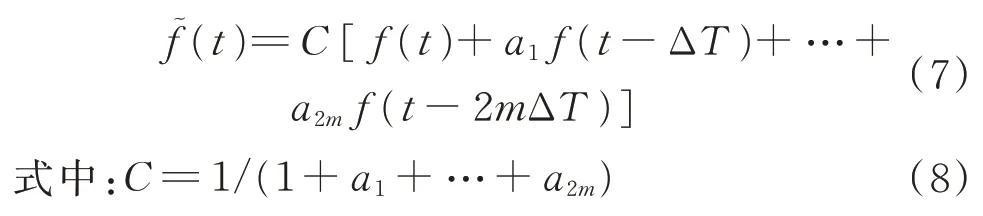
步驟1根據機械臂末端的起點p0和終點pn，將速度函數v(t)選擇為典型的勻加速、勻速和勻減速梯形變速過程。

步驟2對函數v(t)進行整形，得到整形后的速度函數。

步驟3用數值求積法，由速度得到經過整形后的機械臂末端的笛卡爾坐標

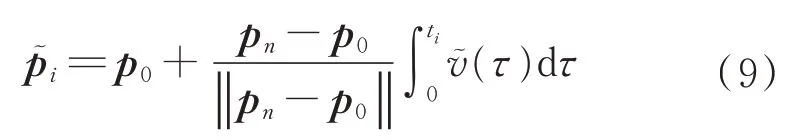
步驟4用逆運動學方法，由笛卡爾坐標求得兩個關 節的轉角 函數。

由于被整形的速度函數滿足條件

即函數v(t)在區間[0，T]以外都等于零，而且整形器常數還滿足關系式（8），那么由整形過程式（7）可得

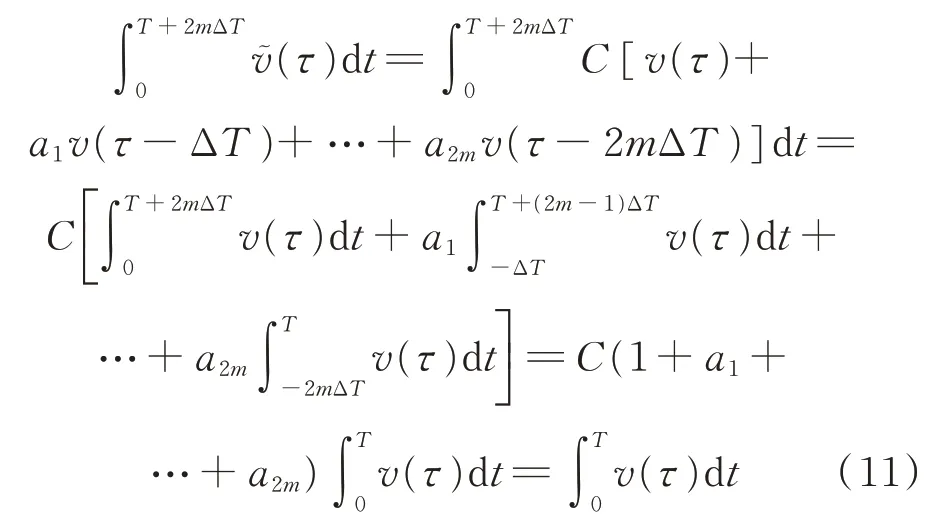
說明對整形后的速度函數進行積分，得到的運行距離與未經整形的結果相同，經過整形后的行程能保證機械臂末端到達相同的終點。

2 機械臂行程及整形設計

2.1 整形器的設計

試驗使用的2 自由度機械臂由2 個臂長度分別為0.30 m 和0.25 m 的直桿構成，如圖3 所示。后臂通過減速比為18∶1 的轉臺（肩關節）連接到支座上，前臂通過相同減速比的轉臺（腕關節）與后臂連接。模擬衛星的重物通過彈性緩沖器安裝在前臂的末端，并在重物上安裝了低頻加速度傳感器。

圖3 輸入整形驗證試驗的2 自由度機械臂Fig.3 Mechanical arm with two degrees of freedom for input shaping validation test

輕微擾動重物，由加速度傳感器測得的自由振動響應信號如圖4所示。數據的采集頻率為1 000 Hz，采樣時間4 s，信號經過上限為6 Hz 的2 階Butterworth 低通濾波。由于實驗的目的在于對比輸入整形對機械臂運行振動的抑制效果，因此，在實驗中僅測量加速度輸出的電壓信號v(t)（V），而沒有標定加速度的絕對量（g或者m/s2）。

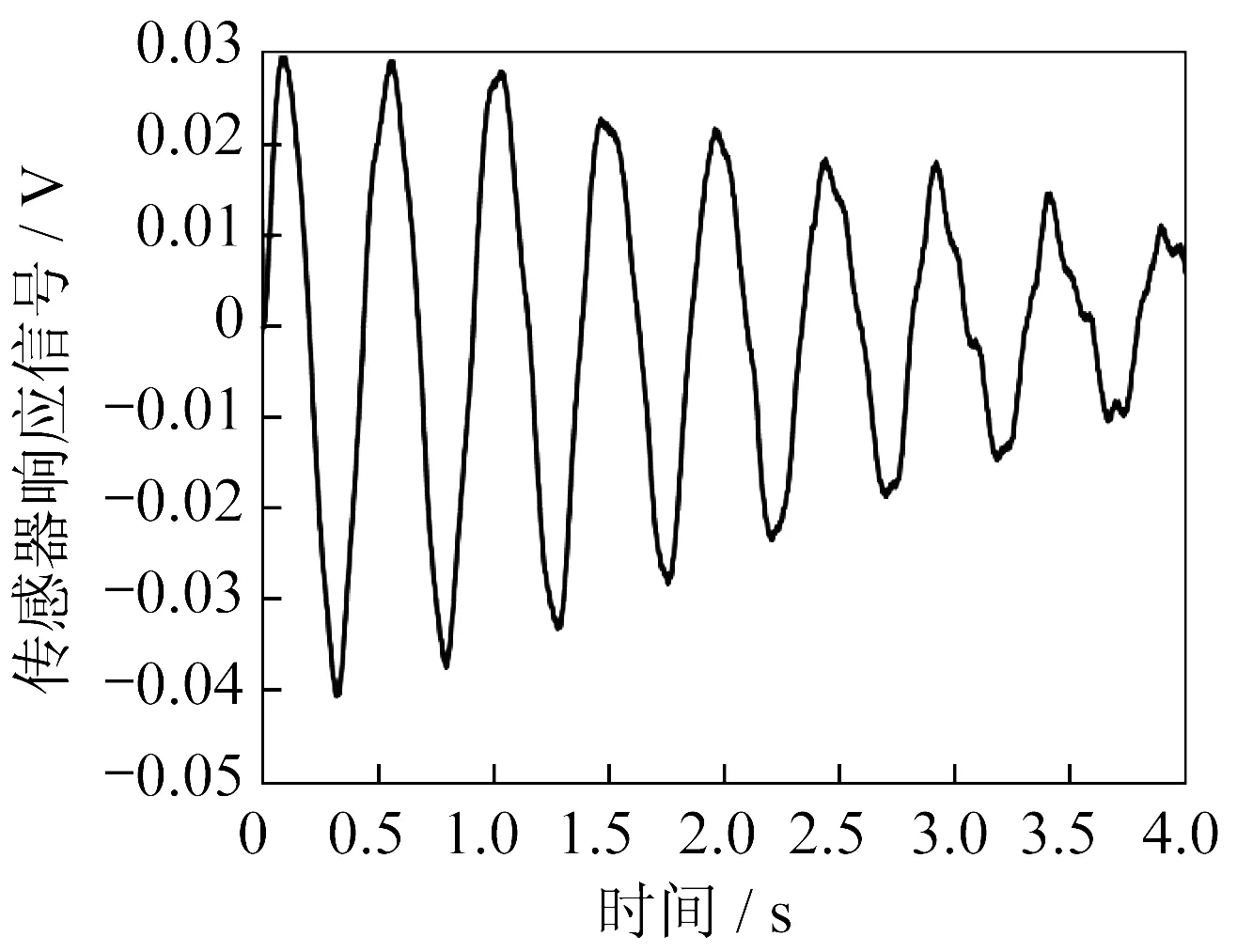
圖4 重物受擾動后的自由振動響應Fig.4 Free vibration response of a heavy object after perturbation

對圖4 的加速度信號v(t)作快速Fourier 變換（FFT），結果V(ω)如圖5 所示（散點×）。

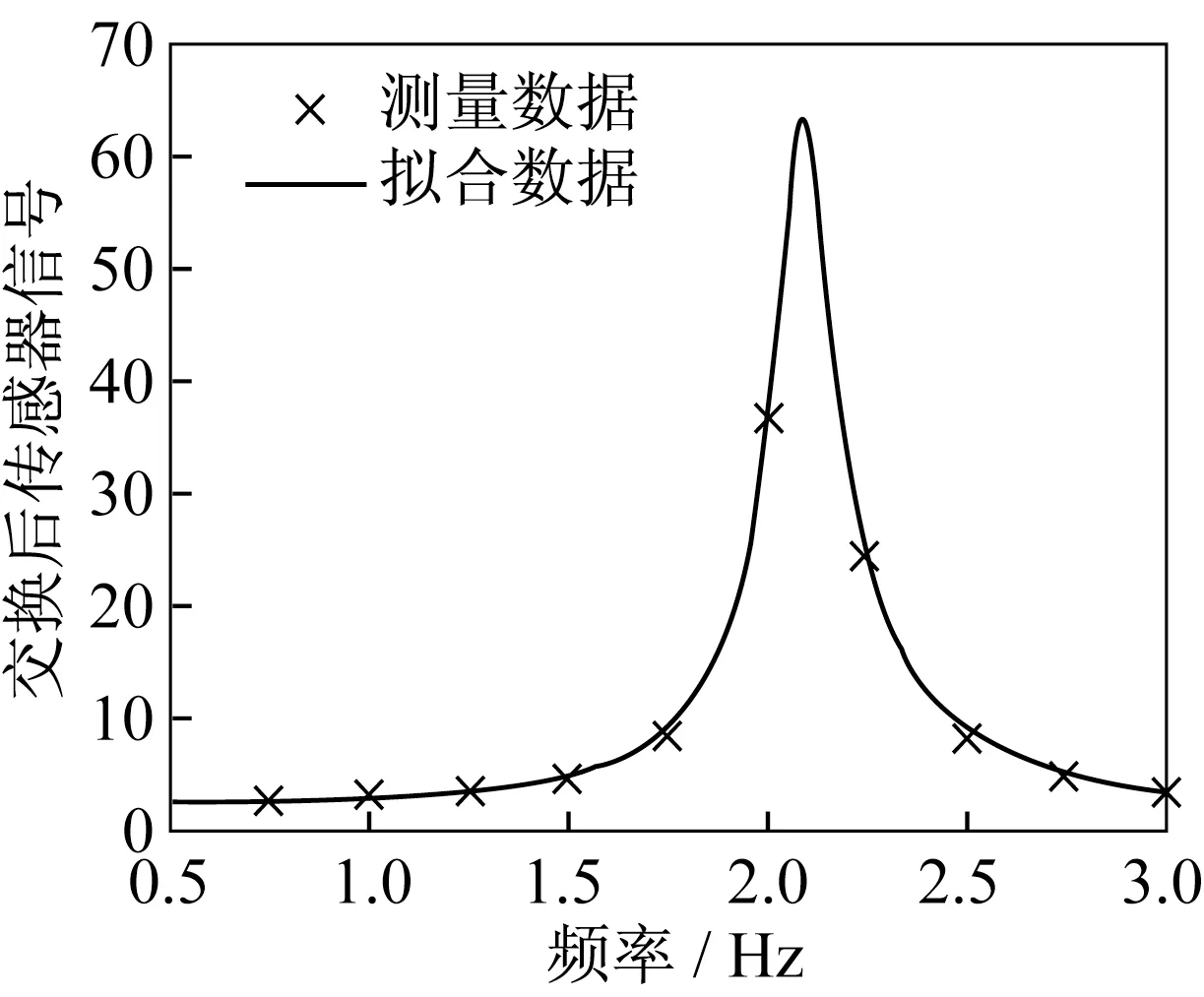
圖5 加速度響應的FFT 變換結果Fig.5 FFT results of the acceleration responses

由于A(ω)僅用于分析結構的固有頻率和阻尼比，因此，圖5 中沒有標出縱軸的單位。采用有理多項式逼近方法［16-17］，對函數V(ω)在頻率區間[0.5，3.0]Hz 進行擬合，得到

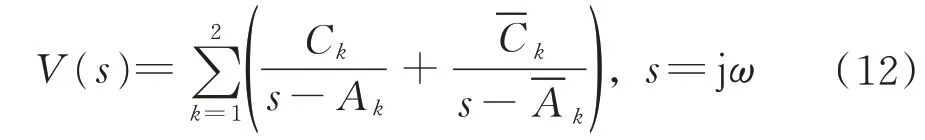
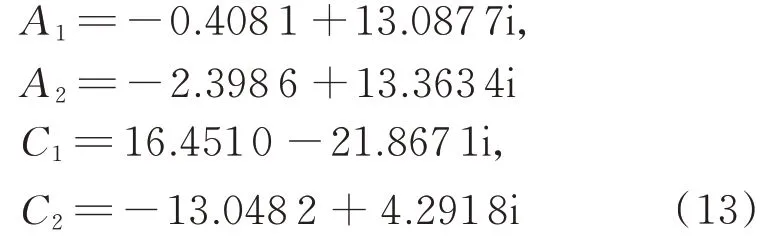
絕對值|V(ω)|的擬合效果如圖5 中的粗實線。

由式（12）可見，模擬衛星的重物安裝在機械臂后，構成的組合體的固有頻率和阻尼比分別是

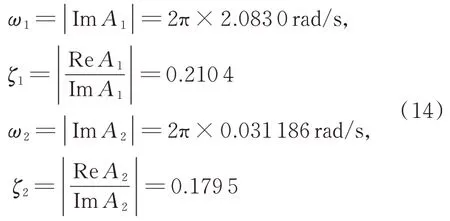
搜索最小延遲量ΔT的時間增量取為Δt=0.025 s，根據式（14）中的頻率和阻尼參數，得到設計結果為

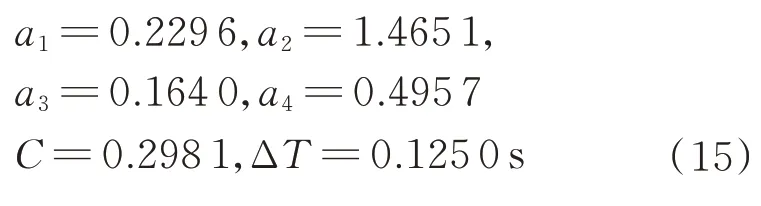
2.2 行程設計和整形

機械臂運行的起點設置在笛卡爾坐標為p0=(384.8，-366.5)mm 的位置上，對應的關節轉角廣義坐標是(-30°，-30°)。終點位于pn=(384.8，366.5)mm 的位置上，對應的關節轉角廣義坐標是(57.209°，-30°)。起點與終點之間的距離為733.01 mm，軌跡如圖6（點劃線）所示。笛卡爾坐標與極坐標的關系不是一一對應的，終點pn的極坐標也可以表示為(30°，30°)，但是在這個極坐標表示下機械臂（粗實線）末端無法從(-30°，-30°)連續運行到(30°，30°)。

圖6 機械臂的運動軌跡Fig.6 Operation route of the mechanical arm

給定起點和終點的坐標后，笛卡爾的行程設計由Matlab 工具箱Robotics Toolbox 完成，結果如圖7所示。在圖7 的上方，實線表示機械臂末端與起點距離隨時間變化的函數，虛線表示機械臂末端運行速度隨時間變化的函數。在圖7 的下方，實線、虛線分別表示機械臂肩關節和肘關節的轉角函數。

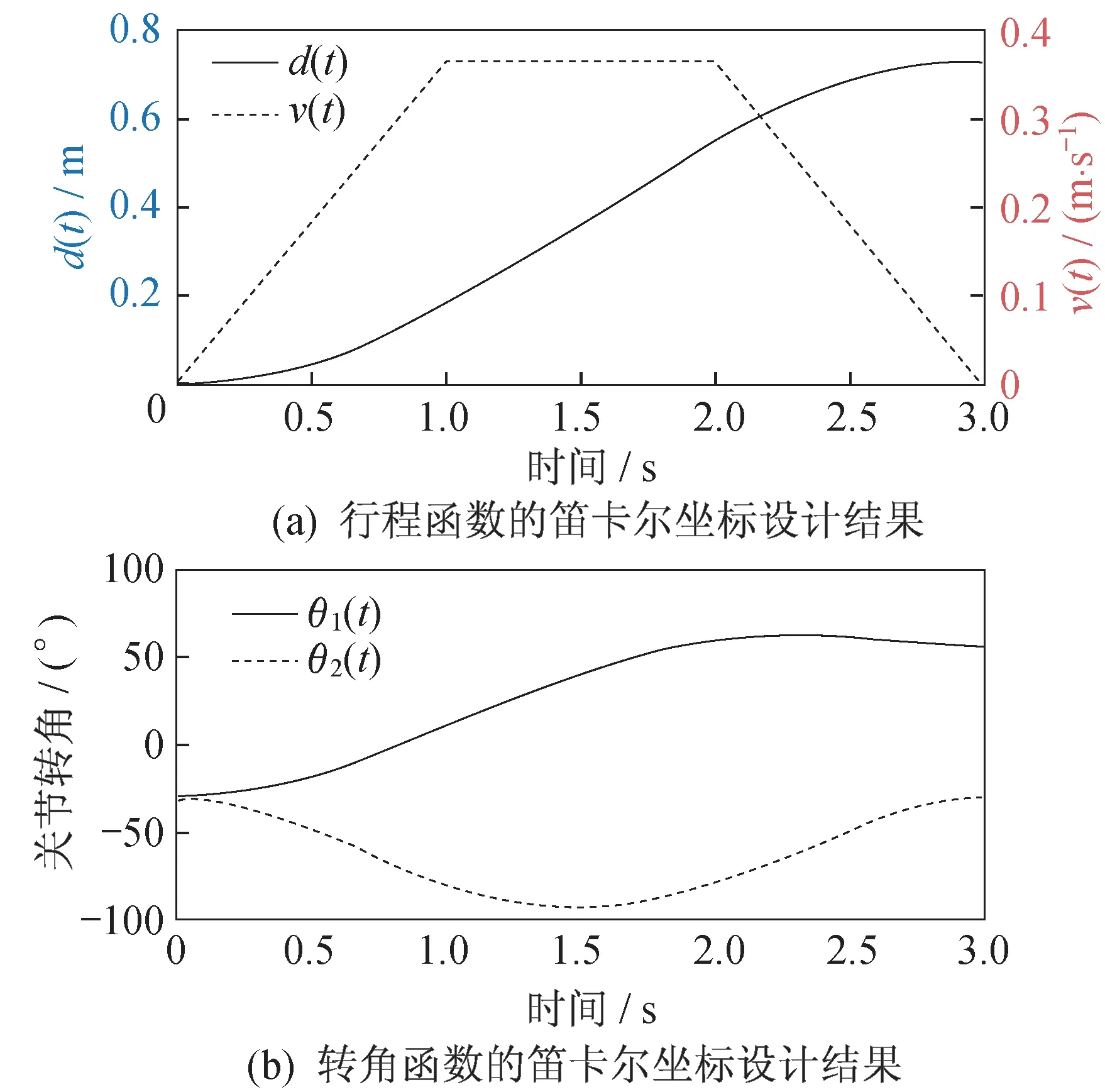
圖7 行程的笛卡爾坐標設計結果Fig.7 Route design results in Cartesian coordinate

選用整形器式（15）對圖7（上方）虛線所示的梯形速度函數進行整形，得到新的速度函數如圖8（上方）的虛線所示。再對整形后的速度函數積分，得到的路程函數如圖8（上方）的實線所示。通過逆運動學求解，可從笛卡爾坐標下的行程得到關節轉角隨時間變化的函數，如圖8（下方）。這部分工作借助Matlab 工具箱Robotics Toolbox 實現。

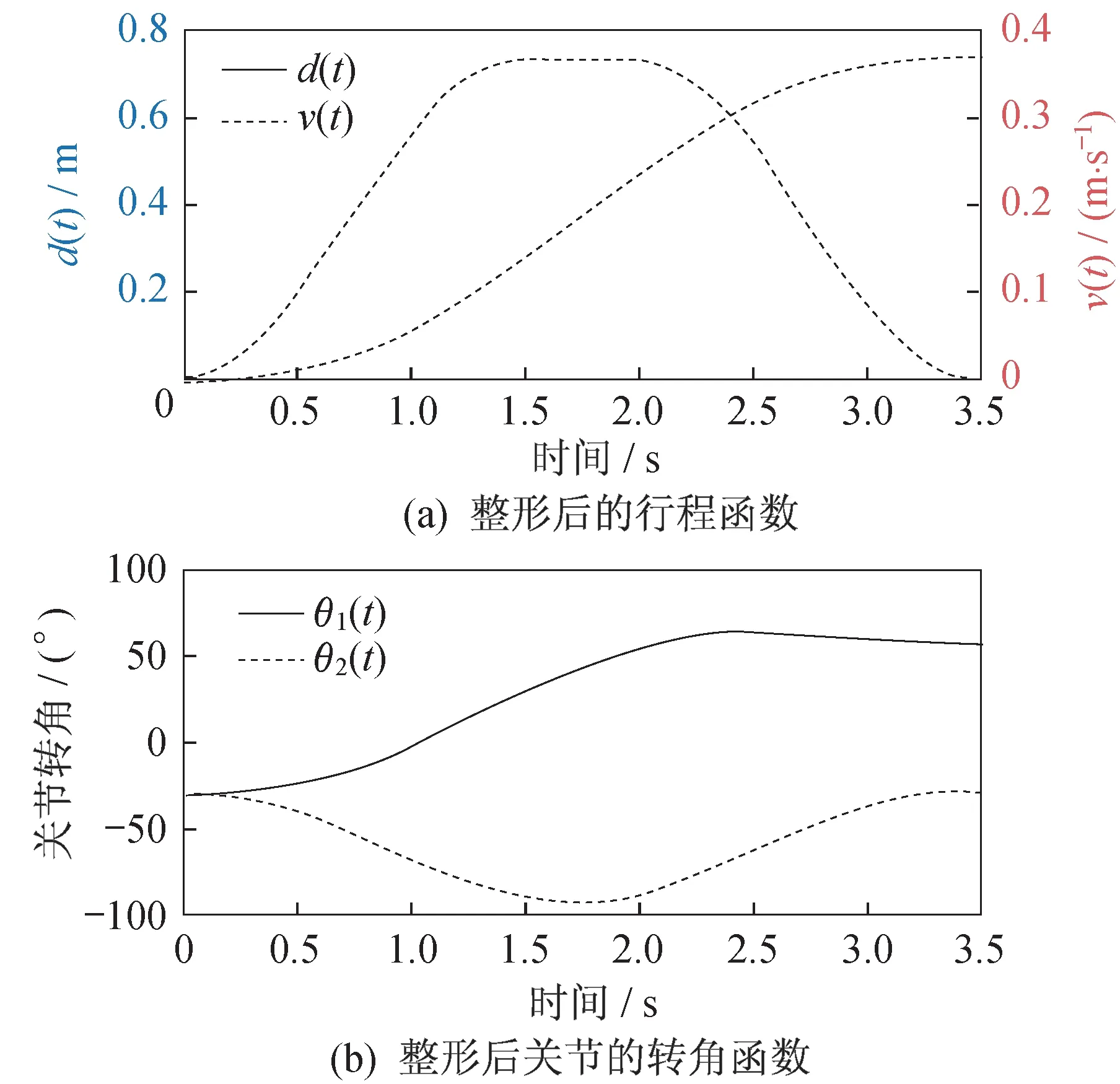
圖8 整形后的行程和關節的轉角函數Fig.8 Functions of routes and rotation angles of joints after input shaping

3 機械臂行程輸入整形的振動抑制效果

按照整形前后關節轉角的時間函數圖7（下方）和圖8（下方）驅動2 自由度機械臂，整個運行過程中加速度傳感器記錄下的響應信號如圖9 所示。機械臂行程經過整形后，組合體上加速度傳感器所測得的最大響應幅值是0.005 093 V。未加整形行程時的最大響應幅值測量結果是0.013 080 V。輸入整形方法將最大響應的幅值抑制到原來的39%。

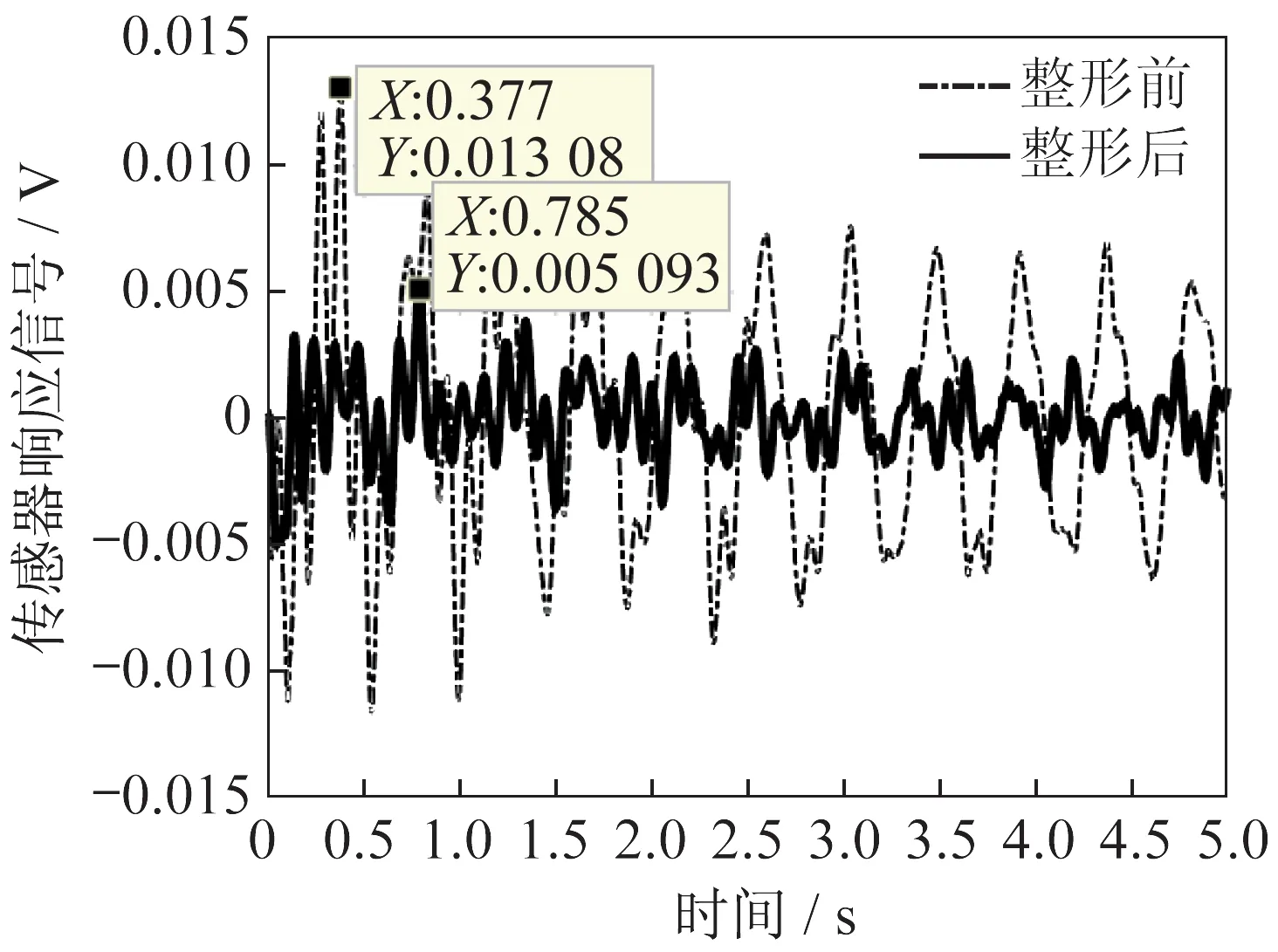
圖9 輸入整形方法對笛卡爾坐標表示下行程的振動抑制效果Fig.9 Effects of vibration suppression to the routes by the input shaping method in Cartesian coordinates

4 結束語

輸入整形技術本質上是對設定的運動歷程進行濾波，通過對搬運過程中機械臂的位移-時間歷程進行整形，使搬運對象在機械臂的控制下沿整形后的運動歷程搬運，將有望達到振動抑制的目的。該技術最大的益處是能完全利用既有的設備，無需增加額外結構或機構的質量。論文以三連桿二關節的2 自由度機械臂為例，進行了行程和輸入整形設計，將整形后的動態響應與逆運動學的解析結果比較，發現輸入整形方法可以大幅降低機械臂的最大響應幅值，達到了振動抑制的目的，證明了方法的有效性。該方法不僅可以拓展到7 自由度機械臂，而且對空間站大型機械臂末端振動抑制也有直接參考意義，具備空間大型柔性結構基座機器人在軌精細控制的應用前景。