基于深度前饋網絡的自適應相對導航濾波

顧冬晴，符 俊，劉曉坤，葉 飚，陳 鳳，王 盈

（1.上海空間機器人工程技術研究中心，上海 201109；2.上海宇航系統工程研究所，上海 201109；3.北京跟蹤與通信技術研究所，北京 100094）

0 引言

在故障衛星維修任務中，獲取相對導航信息是對其進行近距離逼近操控的基本前提。待維修的空間目標具有非合作與姿態翻滾的特點，即目標無法提供合作相對導航信息并且其姿態在空間處于非三軸穩定狀態。國內外一些學者研究了基于卡爾曼濾波的空間非合作翻滾目標近距離相對導航［1-3］，這些研究工作大多利用測量敏感器（如激光成像雷達或雙目相機）提供的相對位姿測量信息，并基于相對軌道與姿態動力學模型以及卡爾曼濾波算法，實現相對導航參數的最優估計。

但是，在工程實踐中由于空間光照環境復雜，各種雜散光都會對測量敏感器產生干擾，從而導致相對位姿測量信息產生異常偏差，進而影響相對導航參數估計精度。因此，研究具有自適應抗差能力的濾波算法，對于空間非合作翻滾目標相對導航技術的工程應用具有現實意義。

深度前饋網絡（Deep Feedforward Network，DFN）也叫做前饋神經網絡（Feedforward Neural Network，FNN）或多層感知機（Multilayer Perceptron，MP）［4］，是典型的深度學習模型，其簡潔、實效的學習功能，為神經網絡技術在各學科領域的廣泛應用提供了一種有效的實現手段。深度前饋網絡由一個輸入層、多個隱層以及一個輸出層構成，對于非線性問題及復雜因素問題具有顯著的優越性，尤其適用于處理非機理性預測問題［5-7］。本文將針對空間非合作翻滾目標近距離相對導航中相對位姿測量存在異常偏差的問題，結合深度前饋網絡優良的學習與預測性能，創造性地提出一種基于深度前饋網絡的自適應濾波方法，并將通過數學仿真分析驗證其有效性。該自適應濾波方法將在卡爾曼濾波估計的基礎上，采用深度前饋網絡智能自適應地檢測與估計測量中存在的異常偏差并給予修正，該深度前饋網絡具有5 個隱層且每個隱層具有10個神經元，網絡輸入向量采用當前測量值以及濾波狀態多步預測進行構造。

1 相對導航濾波模型

從工程應用的角度考慮，為了降低計算復雜度，需要考慮在保證模型準確度的情況下盡可能地降低模型階數。因此，在相對導航濾波建模中對相對姿態與相對軌道動力學模型進行了降階解耦設計，分別提出了12 階相對姿態濾波模型以及相對軌道濾波模型。

1.1 相對姿態濾波模型

跟蹤飛行器本體質心系b 與目標本體質心主慣軸系t 之間的姿態矩陣微分方程可表述為

若忽略目標飛行器所受到的干擾力矩，則目標的姿態動力學方程為

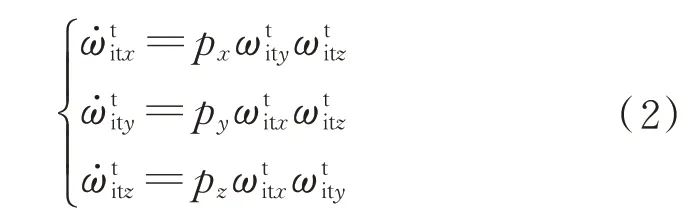
采用激光成像雷達或雙目相機可以獲得b 系和目標本體固連坐標系c 間的相對姿態信息，而c 系與t 系間存在固定的姿態變換關系即為常值矩陣，因此，有=0。

基于式（1）和式（2）并采用相應的數值算法，在獲取初值后可遞推計算得到，由于遞推計算得到的這些計算值存在較大誤差，因此，需要利用相對姿態測量信息并采用濾波估計的方式對這些參數的誤差進行估計，并用誤差估計值對計算值進行反饋修正。

定義如下相對姿態濾波誤差狀態向量：

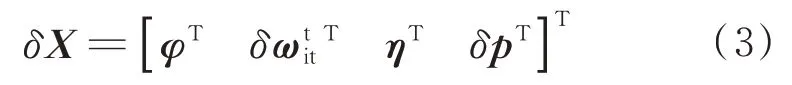
式中：φ為b 系與t 系間姿態誤差角矢量且有為目標轉動角速度誤差矢量且有；η為b 系與c 系間姿態誤差角矢量且有；δp為轉動慣量比誤差矢量且有。

濾波線性化狀態方程為

式中：F為系統矩陣，可由式（1）和式（2）進行線性化得到；W為系統噪聲向量。

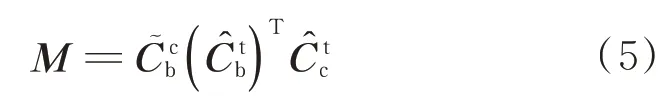
根據矩陣M可構建如下量測向量：

式中：M(i，j)為矩陣M第i行和第j列的元素。

濾波線性化量測方程為

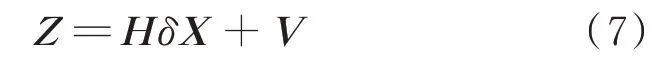
式中：H為量測矩陣，可由式（5）線性化得到；V為量測噪聲向量。

1.2 相對軌道濾波模型

跟蹤飛行器與目標飛行器之間的相對軌道動力學方程為

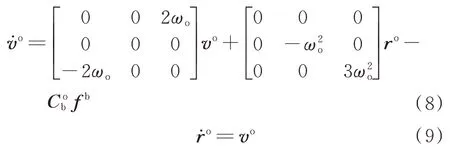
式中：ro為目標飛行器質心相對跟蹤飛行器質心的相對位置矢量在軌道坐標系o 中的投影；vo為相對速度矢量；ωo為軌道角速度；為b 系與o 系間的姿態陣；fb為跟蹤飛行器的比力。另外，目標本體形心相對目標本體質心的桿臂lt為常數，則有l˙t=0。

基于式（8）和式（9）并采用相應的數值算法，在獲取初值后可遞推計算得到，由于遞推計算得到的這些計算值存在較大誤差，因此，需要利用相對位置測量信息并采用濾波估計的方式對這些參數的誤差進行估計，并用誤差估計值對計算值進行反饋修正。

定義如下相對軌道濾波誤差狀態向量：

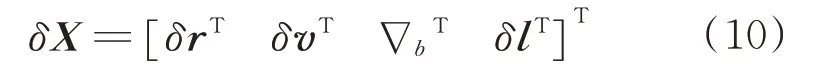
式中：δr為相對位置誤差；δv為相對速度誤差；?b為加速度計常值偏差；δl為桿臂估計誤差。

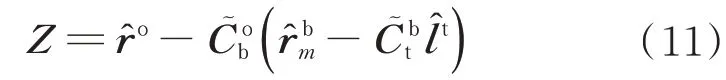
構建如同式（4）和式（7）的相對軌道濾波線性化狀態方程，其系統矩陣F可由式（8）和式（9）線性化得到，量測矩陣H可由式（11）線性化得到。

2 基于深度前饋網絡的自適應濾波

2.1 算法原理

基于上述相對導航濾波模型并利用相對位姿測量信息，可采用擴展卡爾曼濾波（Extend Kalman Filtering，EKF）算法，實現空間非合作翻滾目標相對導航參數的精確估計。但是，在實際工程應用中，由于空間雜散光等干擾因素的存在，使得相對位姿測量信息產生異常偏差，即濾波測量中存在故障干擾。因此，為了保證實際工程應用中濾波估計的魯棒性，提出基于深度前饋網絡的自適應EKF 濾波方法，以避免測量故障干擾影響濾波估計性能。

基于深度前饋網絡的自適應EKF 濾波方法以EKF 算法為基礎，在時間更新完成后對于相對姿態或相對位置測量進行基于深度前饋網絡的智能故障檢測與估計。若檢測出相對姿態或相對位置測量中存在故障即異常偏差，則采用故障估計量對測量進行修正，利用修正后的相對姿態或相對位置測量進行量測更新，其原理框圖如圖1 所示。

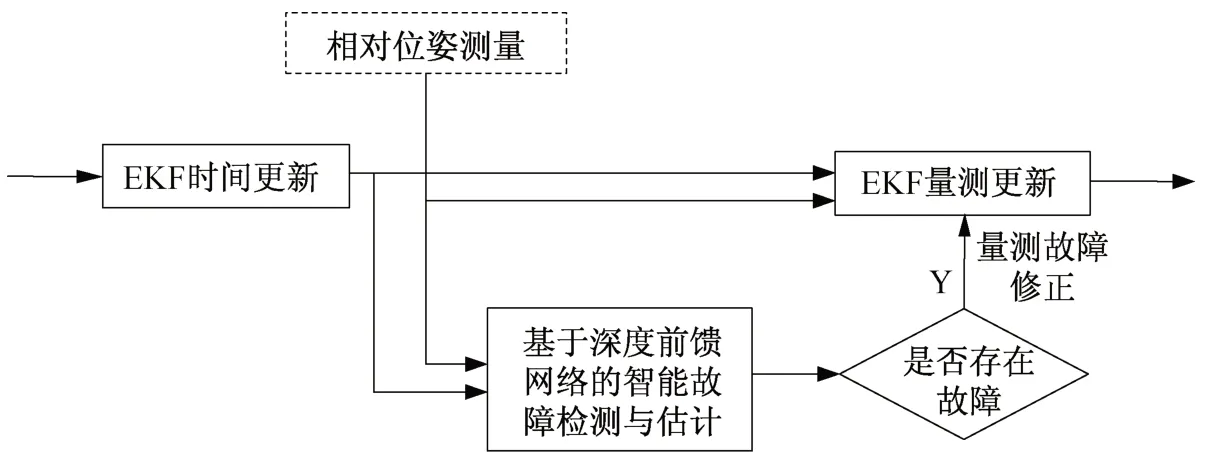
圖1 基于深度前饋網絡的自適應EKF 算法Fig.1 Adaptive EKF algorithm based on deep feedforward network

EKF 時間更新算法為

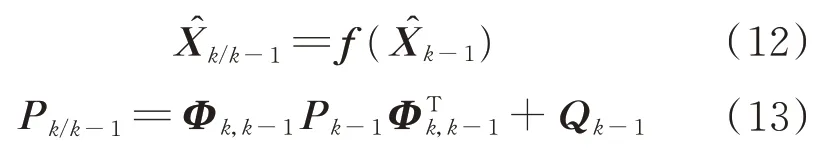
式中：f(·)由相對姿態或軌道動力學模型確定；Φ=I+F?ΔT（ΔT為濾波更新周期）；Q為狀態噪聲協方差陣。

考慮量測故障修正的EKF 量測更新算法：

式中：R為量測噪聲協方差陣；為量測故障估計量，其分量為。在一次測量中，典型的故障形式可用隨機常值模型表示即=a（a為隨機常值），若未檢測出量測向量的分量中存在故障即中分量的絕對值＜εi（εi為檢測閾值），則=0。

2.2 基于深度前饋網絡的智能故障檢測與估計

為相對姿態或相對位置測量的每一個分量設計一個具有5 個隱層的深度前饋網絡，每個隱層有10 個神經元，隱層神經元激活函數為雙曲正切S 型函數。網絡的輸出為故障估計值，輸出層含有1 個神經元，輸出層神經元激活函數為線性函數。在tk時刻，根據式（5）、式（6）和式（7），采用相對姿態或相對位置測量以及濾波狀態一步預測構造的量測向量為Zk/k-1，且有zi，k/k-1（i=1，2，3）為其分量；則tk時刻，由相對姿態或相對位置測量和濾波狀態j步預測構造的量測向量為Zk/k-j，且有zi，k/k-j（i=1，2，…）為其分量；將由相對姿態或相對位置測量和濾波狀態1～10 步預測構造得到的量測向量各分量zi，k/k-1、zi，k/k-2、zi，k/k-3、…、zi，k/k-10，作為每一個網絡的輸入向量。智能故障檢測與估計的深度前饋網絡模型，如圖2 所示。

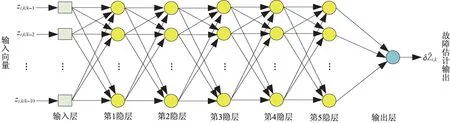
圖2 智能故障檢測與估計的深度前饋網絡模型Fig.2 Deep feedforward network model for intelligent fault detection and estimation

為了對深度前饋網絡進行訓練，需要構造用于訓練的輸入向量樣本及其期望的輸出樣本。首先構造空間非合作翻滾目標近距離相對導航的仿真場景，然后在測量無故障的情況下進行20 組仿真且每組仿真時間為600 s，在量測更新周期為1 Hz 的情況下，每一個深度前饋網絡可以獲得12 000 組輸入向量訓練樣本，且其對應的期望輸出值均為0。在此基礎上，為了構造測量故障情況下的訓練樣本，對于每一個深度前饋網絡隨機生成12 000 個服從均勻分布的實數（均勻分布的范圍可根據具體應用設定），作為其故障情況下訓練樣本的期望輸出值，并將其加入至對應的輸入向量中。如此設計，對于每個深度前饋網絡便有24 000 組訓練樣本，其中12 000 組樣本為無故障情況下的訓練樣本，12 000 組樣本為故障情況下的訓練樣本。

3 數學仿真分析

基于深度前饋網絡的自適應相對導航濾波中，相對姿態與相對軌道濾波方法相同，因此，遵從即保證仿真驗證充分性又避免冗余的原則，僅以相對軌道濾波為例進行數學仿真分析。數學仿真中，設置跟蹤飛行器從距目標60 m 逼近至2 m，并且在30 m、10 m 處進行停泊，并且最終在2 m 處進行懸停，仿真時間600 s。

相對位置測量數據更新周期為1 s，相對位置測量誤差為白噪聲且其標準差為0.03 m，并且用于訓練深度前饋網絡的均勻分布故障樣本的數值范圍設置為±1.0 m 之間，即故障樣本數值上限約為測量誤差標準差的33 倍，以確保數值上能夠充分覆蓋不易檢測的故障。

相對軌道濾波仿真中，對于x軸相對位置測量在300～310 s 時間段額外增加了-0.30 m 偏差，對于y軸相對位置測量在400～410 s 時間段額外增加了0.35 m 偏差，對于z軸相對位置測量在500～510 s時間段額外增加了-0.40 m 偏差。采用基于深度前饋網絡的自適應EKF 以及EKF 的相對位置與相對速度誤差曲線如圖3 和圖4 所示，深度前饋網絡對于測量偏差的估計曲線如圖5 所示。

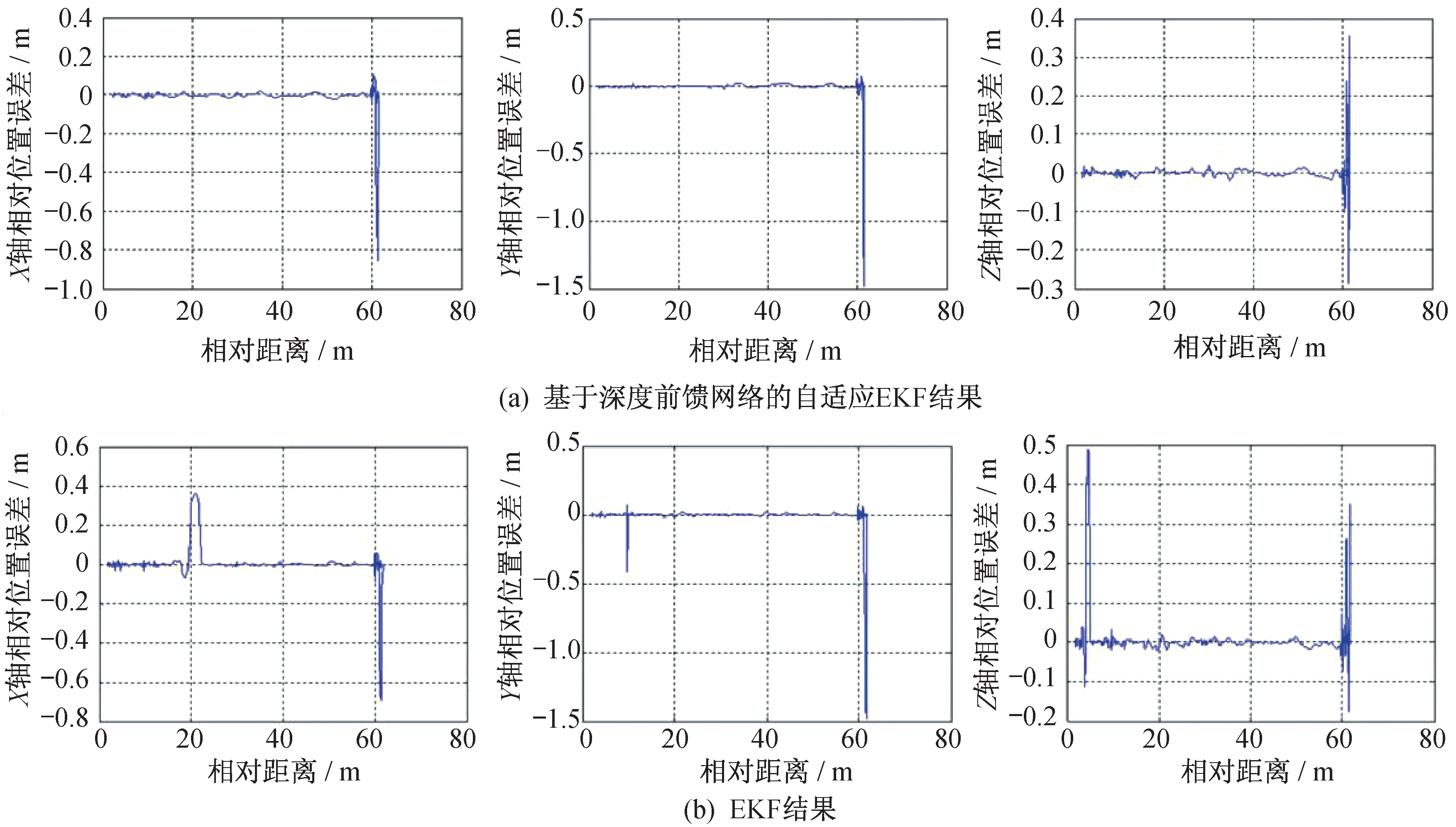
圖3 相對位置誤差Fig.3 Relative position errors

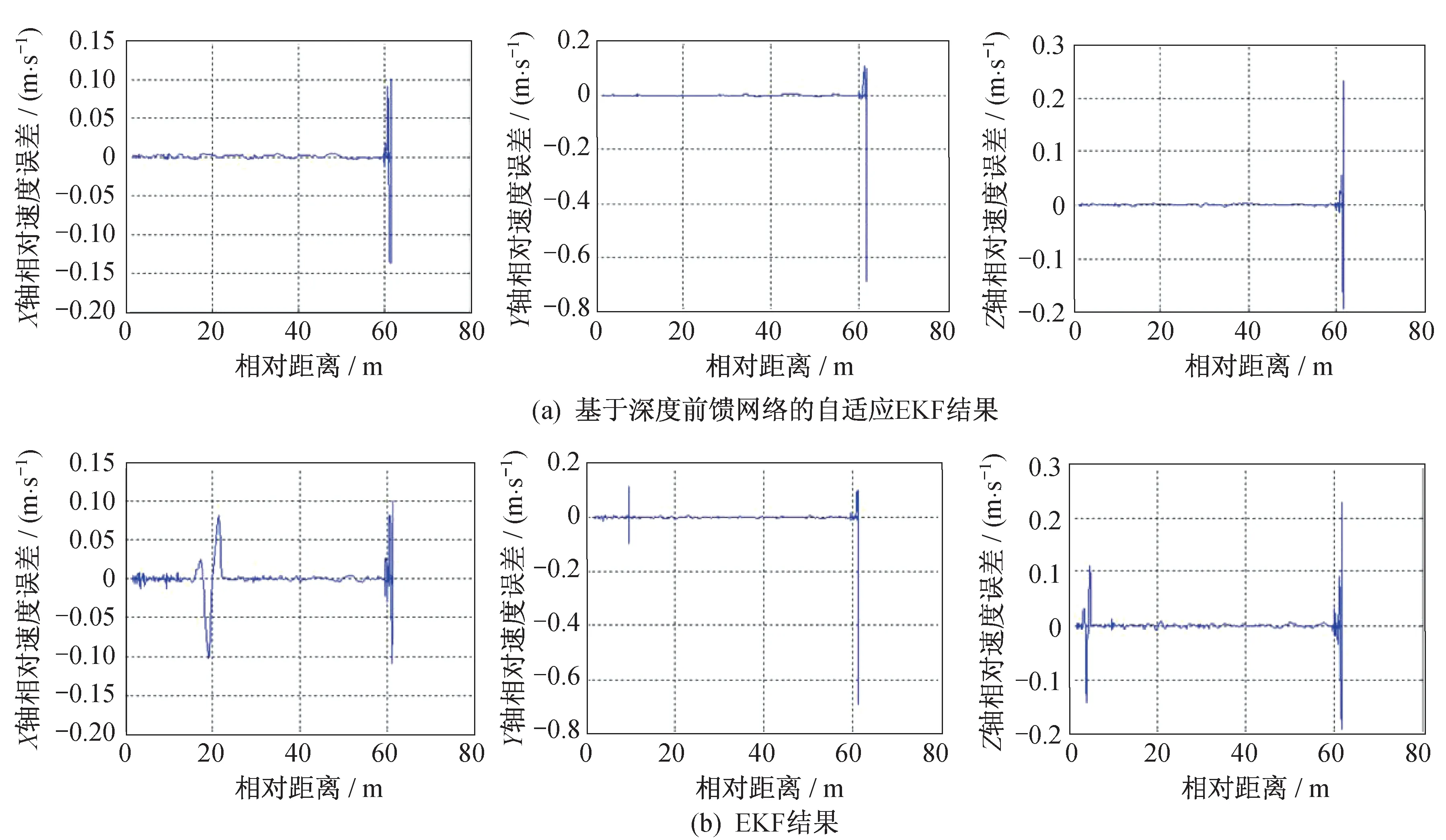
圖4 相對速度誤差Fig.4 Relative velocity errors

由圖3 和圖4 可見：當存在測量異常偏差的情況下，相對軌道濾波EKF 結果受測量異常偏差影響較大，相對位置和相對速度誤差均產生突然變大的情況；而基于深度前饋網絡的自適應EKF 結果基本不受測量異常偏差影響，濾波收斂后相對位置誤差均小于0.02 m，相對速度誤差均小于0.02 m/s。由圖5 可見：深度前饋網絡能夠有效估計相對位置測量異常偏差，估計誤差小于異常偏差值的15%。

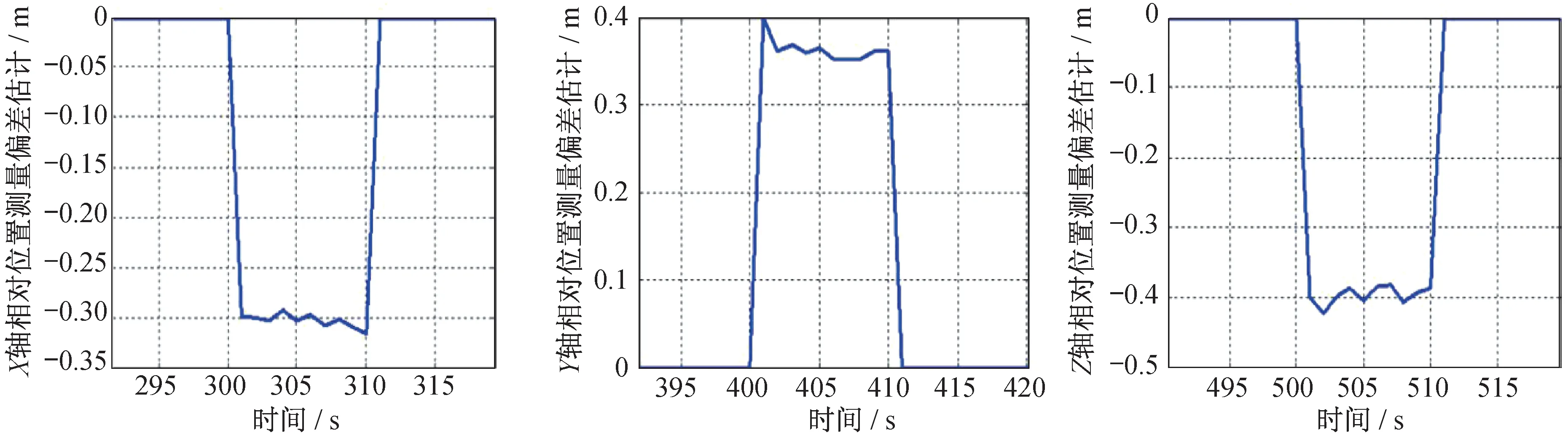
圖5 相對位置測量偏差估計Fig.5 Estimation for the measurement offset of the relative position

4 結束語

在軌維修任務最終逼近目標的過程中，需要采用空間非合作翻滾目標近距離相對導航技術，該技術在工程應用中將面臨空間雜散光干擾致使測量值出現偏差，進而導致相對導航濾波精度下降的問題。本文針對該問題，提出了基于深度前饋網絡的自適應相對導航濾波方法，并且數學仿真分析結果表明，當存在測量異常偏差的情況下，深度前饋網絡能夠有效估計異常偏差，且基于深度前饋網絡的自適應EKF 結果顯著優于常規EKF。因此，本文提出的方法能夠較為有效地解決異常測量值導致相對導航精度下降的問題，具有較好的工程實踐應用價值。