斷裂問題在路面工程中的研究進展

劉琬辰

（山東省交通規劃設計院有限公司，山東 濟南 250031）

引言

路面在使用過程中出現的各種各樣的破壞問題中，開裂病害極具普遍性和嚴重性。由于裂縫尖端的特殊性，傳統強度理論回答不了此類問題 ，而斷裂力學提供了新的思路。與此同時，數值計算科學的發展填補了斷裂力學對于復雜問題無法獲得解析解的空白。兩者相輔相成，促進了路面斷裂的分析研究。

1 理論發展

路面開裂研究的理論基礎是斷裂力學。從斷裂力學的確立到發展至今不到百年，基本可以歸納為三個階段：線彈性斷裂，疲勞斷裂，彈塑性斷裂［1］。20 世紀60 年代末、70 年代初斷裂力學被引入路面研究中。

1.1 線彈性斷裂

1.1.1 Griffith 理論和應力強度因子

1921 年英國科學家Griffith 最先從探究玻璃的實際強度的原因出發，提出脆性材料的斷裂應力與材料裂紋尺寸有關，并用應變能釋放率來表征裂紋擴展力。1957 年Irwin 針對具有含裂紋板，應用彈性理論解得各點應力分量，從表達式中提煉出與荷載和裂紋尺寸有關的的系數作為決定裂紋端部應力場強度的參量，稱之應力強度因子K。

1.1.2 路面工程領域的線彈性斷裂研究

20 世紀70 年代，Kauffman［2］將斷裂力學的概念引入到路面結構的設計思想中，并用線彈性斷裂理論預測路面開裂問題。隨后的80 年代，Monismith［3］等人用線彈性斷裂理論研究了基層反射裂縫裂縫問題，對加鋪層的應力分布進行分析。Abdulshafi［4］等人使用盤狀試件結合線彈性斷裂的概念研究了瀝青混合料的斷裂問題［12］。

國內方面,周富杰［5］對舊水泥路面上瀝青層罩面反射裂紋進行力學分析，認為裂紋尖端的應力強度因子KI，控制著裂紋初期的擴展，KII控制著裂紋后期的擴展。吳贛昌［6］對裂縫尖端的應力強度及其與路面溫度分布和路面材料特性參數的關系進行了數值分析。

1.2 疲勞斷裂

用什么參量來描述裂紋擴展，裂紋擴展的推動力是什么，這是疲勞裂紋擴展規律研究中最關鍵的問題。斷裂力學是研究疲勞裂紋擴展的一個有用工具和常用方法。

1.2.1 Paris 疲勞壽命預測

1962 年，Paris 提出一個為工程界廣泛采用的疲勞裂紋擴展速率的半經驗公式：

式中:a—裂紋長度；N—荷載作用次數；C、n—材料常數；ΔK—應力強度因子幅值。成功地將應力強度因子，裂紋長度，荷載作用次數聯系在一起。對公式積分可得到裂紋生長到指定長度時的壽命。

1.2.2 對Paris 公式的修正

Slowik 等人［7］結合混凝土的特性，提出在公式右邊增添一個加項F（a， σ），表征混凝土裂紋在突加荷載情況下的力學響應，是與裂紋長度和突加荷載大小有關的函數。

Majidzadeh 等人［8］于1977 年將斷裂力學原理應用于瀝青混合料，總結出可用于瀝青混合料的Paris裂縫擴展的一般形式：

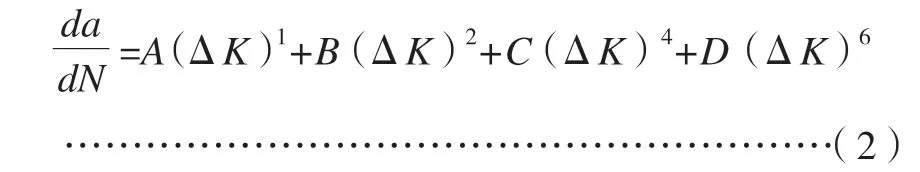
式中：A,B,C,D—材料斷裂參數。

隨后Schapery［9］對Paris 公式修正，描述黏彈性材料I 型裂縫擴展過程，只是式中的C 和n 有另外求解形式。

Jacobs［10］在Schapery 的理論上額外考慮瀝青混合料的空隙和集料顆粒會影響裂紋擴展，提出參數的修正公式。

1.3 彈塑性斷裂力學

材料在裂紋擴展前，端部都將出現塑性區，塑性區尺寸很小時，可以近似看成線彈性斷裂問題。但當外荷載較大時，塑性區尺寸急劇增長，此時就需要彈塑性斷裂理論加以研究。

1.3.1 J 積分

1968 年，針對彈塑性斷裂問題，Rice 提出即J積分理論，考慮對任意一個圍繞裂紋尖端的逆時針回路進行積分，巧妙地繞過裂縫端部復雜的應力應變場而獲得彈塑性斷裂問題中的裂紋力學參量。

1.3.2 內聚力模型

CZM（Cohesive Zone Model）是由Dugdale 和Barenblattt首先提出，自20 世紀70 年代起，CZM 被大量應用于水泥混凝土研究中，并逐步引入瀝青混凝土領域。

CZM 將物理斷裂區域限定在內聚力范圍內，這個區域由兩個虛擬的面所包圍，界面上作用有內聚力。界面上的內聚力和界面的張開位移共同定義了內聚力區域的本構關系。對內聚力—位移曲線下的面積通過積分，可得到內聚力區域斷裂能的計算公式，表述了材料的內聚關系。

國內有關研究［11］利用修正參數后的雙線性CZM 模型，用數值模擬的方法，進行瀝青混合料的劈裂試驗，對比室內SCB 試的結果，進一步驗證了雙線性模型模擬瀝青混凝土斷裂行為的有效性，同時分析了試驗過程中試件的應力分布和裂縫的形成與擴展。

1.3.3 瀝青混合料的熱粘彈性斷裂

瀝青混合料是典型的流變材料，其力學響應不僅依賴當前應力狀態和環境溫度，還與加載歷史（黏彈性）和溫變歷史（熱彈性）有關。

有關瀝青混合料的黏彈性的本構模型經歷了Maxwell 模 型、Kelvin 模 型、Burgers 模 型 和 廣 義Kelvin 模型的發展過程。再依據時溫等效性原理，可以將溫變因素對材料力學性質的影響通過時間尺度來折算。

2 數值計算發展

2.1 有限元原理

有限元法是根據變分原理求解數學問題的一種數值計算方法。將實體經網格劃分離散化，針對單元選定位移模式，結合幾何方程、物理方程和平衡方程，再整合到整體，得到整個結構的平衡方程。

式中： ［K］—整體剛度矩陣；｛F｝—荷載及邊界條件；｛δ｝—未知應力。

在已知荷載作用條件下，考慮幾何邊界條件后，能夠解出所有節點應力或位移（位移可以通過物理方程與應力聯系）。

2.2 特殊單元

裂縫尖端奇異性決定了裂縫尖端附近采用的由參單元退化以后可得到奇異單元而非常規單元，該單元退化邊為裂縫前端，并將中間結點移至靠近裂縫尖端1/4 單元邊長時即可滿足裂縫尖端的奇異性。

在考慮路面面層受到汽車制動或啟動產生的水平力時，采用表面效應單元可以將作用在其上的荷載轉化為均布荷載作用，從而模擬實際中路表面受到水平均布荷載的作用情況。

利用數值計算方法模擬路面結構中的夾層，常常通過將夾層材料近似成具有一定厚度的彈性材料；或是采用薄膜單元和界面單元，分別表征夾層材料和層間接觸情況。兩種單元各自有相應的剛度矩陣，形函數和坐標轉換矩陣。

2.3 熱黏彈性斷裂的有限元計算

熱黏彈性本構關系（采用時間增量型本構關系）引入到對瀝青面層的描述中，一般考慮采用：

2.4 傳統裂紋擴展過程的模擬

對傳統的裂紋擴展，一般思路是借助有限元軟件對外荷載作用下的裂紋端部進行應力場分析，判斷失穩擴展條件：

式中：K*—混合型應力強度因子；KIC—斷裂韌度，由試驗測得；θ*—擴展角，由方程解得：

沿該方向對裂縫長度增加，Δα并再次計算裂紋的應力場，依此思路逐步模擬裂紋擴展過程［12-13］。其間需克服的困難是裂紋擴展過程中的網格不連續問題。

2.5 擴展有限元與廣義有限元

擴展有限元與廣義有限元是近十年來處理裂縫問題的先進技術。兩者的核心思想是一致的［14-15］，不同之處僅限于單元結點處自由度的物理涵義不同，所采用的數值積分技術也不同。在利用廣義有限元和擴展有限元處理路面開裂問題時，兩者的差異并不會影響結果。

總體來說，GFEM 和XFEM 在模擬路面結構裂縫問題方面的優勢明顯：（1）網格劃分不依賴結構體，極好地解決了裂縫區域的網格劃分問題。（2）智能化全程化地模擬擴展路徑，包含了裂縫萌生和擴展的全過程。

Hasan Ozer［16］以斷裂力學為基礎，以廣義有限元為手段，利用高次等效區域積分法對柔性路面裂縫的宏觀參量進行計算，評價分析了路面模型中的60 種不同裂縫的應力狀態和擴展路徑。國內有相關人士利用擴展有限元分析了路面反射裂紋的斷裂問題［17］和路表面自上而下裂紋的二維擴展［18］。

3 結語

基于斷裂力學的黏彈性力學方面的應用研究工作主要集中在瀝青混合料的黏彈性及低溫抗裂指標的實驗研究及瀝青路面溫度應力計算方面，應用黏彈性斷裂力學理論與方法進行理論分析方面的工作尚待擴充。

到目前為止，基于斷裂力學的路面開裂縫問題的研究基本限于靜態加載或緩慢加載下的裂紋擴展問題。對于重載比例擴大化，涉及到與時間有關的裂紋快速起裂、擴展或止裂問題等屬于動態斷裂力學范疇的研究將更加廣泛。