高超聲速飛行器平衡滑翔狀態(tài)變量的求解

孟繁卿，田康生

(空軍預(yù)警學(xué)院a.研究生大隊(duì)；b.四系，湖北 武漢 430019)

0 引言

高超聲速飛行器是一種具備顛覆性的新型武器運(yùn)載平臺(tái)，不僅具備超遠(yuǎn)距離投送能力，而且飛行速度為高超聲速、彈道軌跡靈活多變。當(dāng)前的各種導(dǎo)彈防御系統(tǒng)在面對(duì)高超聲速飛行器時(shí)，尚難以實(shí)現(xiàn)有效攔截，高超聲速飛行器因此被視為改變戰(zhàn)爭(zhēng)規(guī)則的殺手锏武器[1]。高超聲速滑翔飛行器作為高超聲速飛行器的一種，通過火箭助推或天基平臺(tái)釋放到達(dá)一定高度后進(jìn)入滑翔狀態(tài)。其在滑翔段借助空氣動(dòng)力實(shí)現(xiàn)滑翔飛行，飛行速度Ma大于5，飛行高度大于20 km。

文獻(xiàn)[2]通過對(duì)飛行器運(yùn)動(dòng)方程無量綱化和規(guī)范化，在對(duì)運(yùn)動(dòng)方程簡(jiǎn)化的基礎(chǔ)上利用解析積分求得了狀態(tài)變量的一階解析解，進(jìn)一步利用解析延拓方法求得了狀態(tài)變量的二階解析解。文獻(xiàn)[3]利用解析積分求得了飛行器滑翔段射程的近似解析式，提出并證明了采用最大升阻比平衡滑翔可獲得最大射程的結(jié)論。文獻(xiàn)[4]利用譜分解的方法求解了平衡滑翔橫向航程、縱向航程和方位角的解析解，基于所求解析解設(shè)計(jì)的再入制導(dǎo)律，能滿足多種任務(wù)需求，且對(duì)初始狀態(tài)誤差不敏感。文獻(xiàn)[5]采用正則攝動(dòng)的方法求解了平衡滑翔高度、速度傾角和縱向加速度的解析解，利用所求解析解設(shè)計(jì)了一種控制平滑、彈道收斂快，且具有良好魯棒性的平衡滑翔方案。文獻(xiàn)[6]在常升阻比條件下，通過查找有理函數(shù)積分表，求解了射程、飛行高度和速度之間的關(guān)系式，分析了不同初始狀態(tài)時(shí)的彈道特性。文獻(xiàn)[7]利用平衡滑翔條件求解了飛行器射程的解析解，分析了升阻比、初始狀態(tài)等參數(shù)對(duì)彈道射程的影響，從能量的角度提出了彈道方案的選擇方法。

通過對(duì)以上文獻(xiàn)的分析可知，對(duì)飛行器運(yùn)動(dòng)規(guī)律，即飛行器狀態(tài)變化規(guī)律的分析至關(guān)重要[8-9]。為此，本文對(duì)高超聲速滑翔飛行器在縱向平衡滑翔情況下，飛行器狀態(tài)變量的解析表達(dá)式進(jìn)行了求解分析，以期為目標(biāo)跟蹤模型構(gòu)建、彈道軌跡預(yù)測(cè)、彈道特性分析、目標(biāo)預(yù)警探測(cè)等提供參考。

1 高超聲速滑翔飛行器運(yùn)動(dòng)模型

根據(jù)高超聲速滑翔飛行器在滑翔段的受力情況，建立其運(yùn)動(dòng)方程[10-11]:

(1)

式中：v為飛行速度；γ為速度傾角；(x,z)為飛行器的位置坐標(biāo)；m為飛行器質(zhì)量；g0為重力加速度常數(shù)；L為飛行器所受升力；D為飛行器所受阻力。

其中升力、阻力的計(jì)算可由式(2)求得

(2)

式中：S為飛行器的參考面積；CL為飛行器的升力系數(shù)；CD為飛行器的阻力系數(shù)[12]；ρ為大氣密度，如式(3)所示：

ρ(z)=ρ0ez/ξ，

(3)

在此采用指數(shù)模型計(jì)算飛行器所在高度的大氣密度，ρ0為海平面大氣密度常數(shù)1.225 kg/m3；ξ為歸一化高度常數(shù)8 434 m；R0為地球平均半徑，取為6 371 km。

縱向平衡滑翔是飛行器在縱向平面受力平衡，需要滿足平衡滑翔條件[13-14]：

(4)

飛行終端約束式為

Ω={(xf,zf)||zf|≥hf,|xf-xt|≤df}，

(5)

式中：(xf,zf)為滑翔段結(jié)束時(shí)刻飛行器的位置坐標(biāo)；xt為目標(biāo)點(diǎn)橫坐標(biāo)；hf為終端高度約束；df為滑翔段結(jié)束時(shí)刻飛行器與目標(biāo)點(diǎn)的距離約束。

2 飛行器狀態(tài)變量數(shù)值解

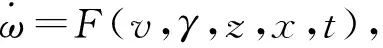
(6)

式中：ti=t0+iΔt,(i=0,1,2,…);Δt為迭代時(shí)間步長(zhǎng)。

3 平衡滑翔狀態(tài)變量求解

3.1 飛行速度、縱程和高度

由平衡滑翔條件式(4)可得

(7)

所以可推導(dǎo)出飛行速度表達(dá)式為

(8)

式(8)對(duì)z求微分可得

(9)

又因?yàn)?/p>

(10)

將式(1)代入式(10)可得

(11)

由式(7),(9)和式(11)可得

(12)

又因?yàn)?/p>

(13)

將式(1)代入式(13)可得

(14)

將式(2)代入式(14)可得

(15)

將式(7)代入式(15)可得

(16)

對(duì)式(16)整理可得

(17)

將式(12)代入式(17)整理可得

(18)

對(duì)式(18)積分可得

(19)

式(19)中Cx為常數(shù)，將式(12)代入式(19)可得飛行縱程x的解析式:

(20)

由式(8)和式(12)可得

(21)

對(duì)式(21)整理可得

(22)

由式(3)和式(22)可得z的解析式為

(23)

3.2 速度傾角

因?yàn)槠胶饣鑿椀佬铦M足平衡滑翔條件，速度傾角變化率為0，且文獻(xiàn)[16]已證明速度傾角為負(fù)的小量，所以無法通過理論推導(dǎo)求出速度傾角的解析表達(dá)式。為了求解速度傾角的近似解，通過龍格-庫(kù)塔求得速度傾角的數(shù)值解，利用正交多項(xiàng)式擬合速度傾角的數(shù)值解[17]。分別采用1,2,3階正交多項(xiàng)式擬合速度傾角的數(shù)值解，擬合函數(shù)分別如式(24)～(26)所示，P0(t),P1(t),P2(t),P3(t)為擬合函數(shù)的基函數(shù)，其中Pj(t),(j=0,1,2,3)是關(guān)于t的j次正交多項(xiàng)式。

γ(t)=d0P0(t)+d1P1(t),

(24)

γ(t)=d0P0(t)+d1P1(t)+d2P2(t),

(25)

γ(t)=d0P0(t)+d1P1(t)+d2P2(t)+d3P3(t).

(26)

(27)

(28)

3.3 仿真校驗(yàn)及分析

為驗(yàn)證平衡滑翔條件下所求狀態(tài)變量解的正確性，以美國(guó)洛克希德·馬丁公司研發(fā)的高超聲速通用氣動(dòng)飛行器CAV-H(common aero vehicle)為例[18]。取目標(biāo)點(diǎn)位置(4 000×103，-100)，飛行器以最大升阻比攻角α=12°飛行，hf=20 km，df=200 km。其滑翔段初始狀態(tài)為，v0=6 078.383 m/s，γ0=-0.085 7°，x0=0，z0=-54.006×103。

如圖1所示為速度傾角數(shù)值解與近似解，圖2為不同階次近似解的RMSE。由圖2可知，速度傾角的一階近似解存在較大誤差，說明平衡滑翔條件下速度傾角與飛行時(shí)間不滿足線性關(guān)系。二階近似解和三階近似解均能很好的表征速度傾角的變化規(guī)律，但三階近似解的精度更高。

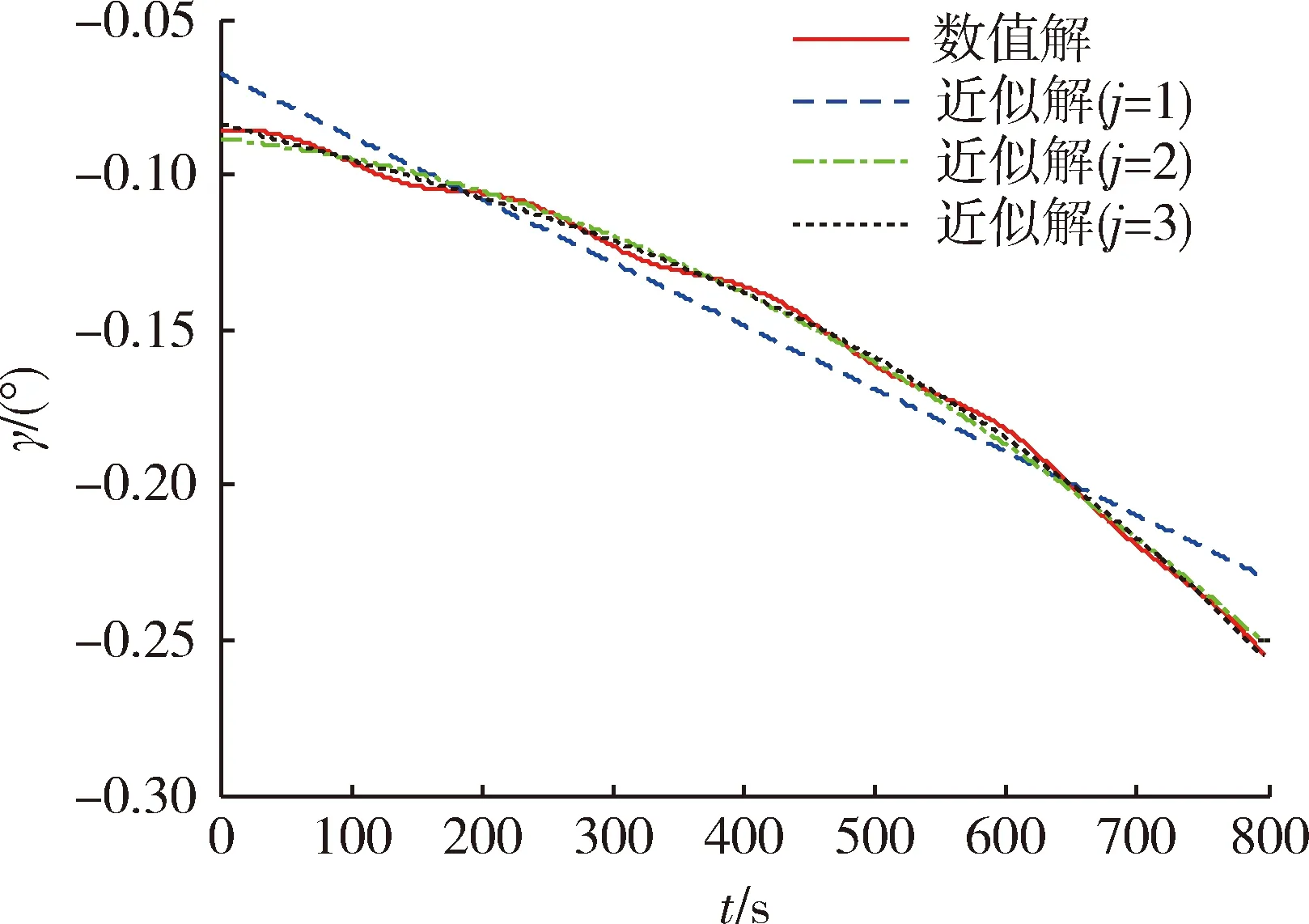
圖1 速度傾角數(shù)值解與近似解Fig.1 Numerical and approximate solution of flight path angle

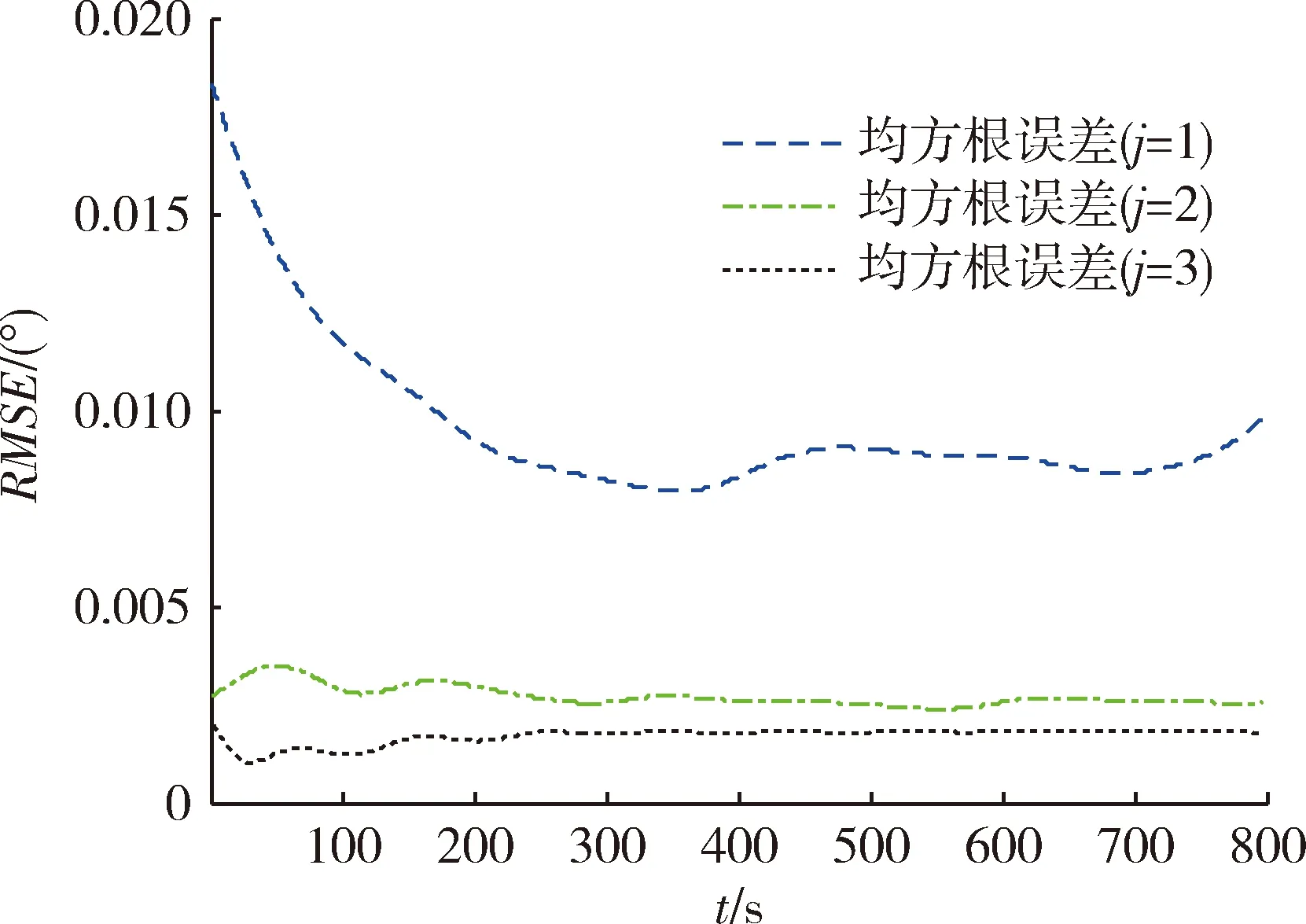
圖2 速度傾角近似解的RMSEFig.2 Approximate solution RMSE of flight path angle

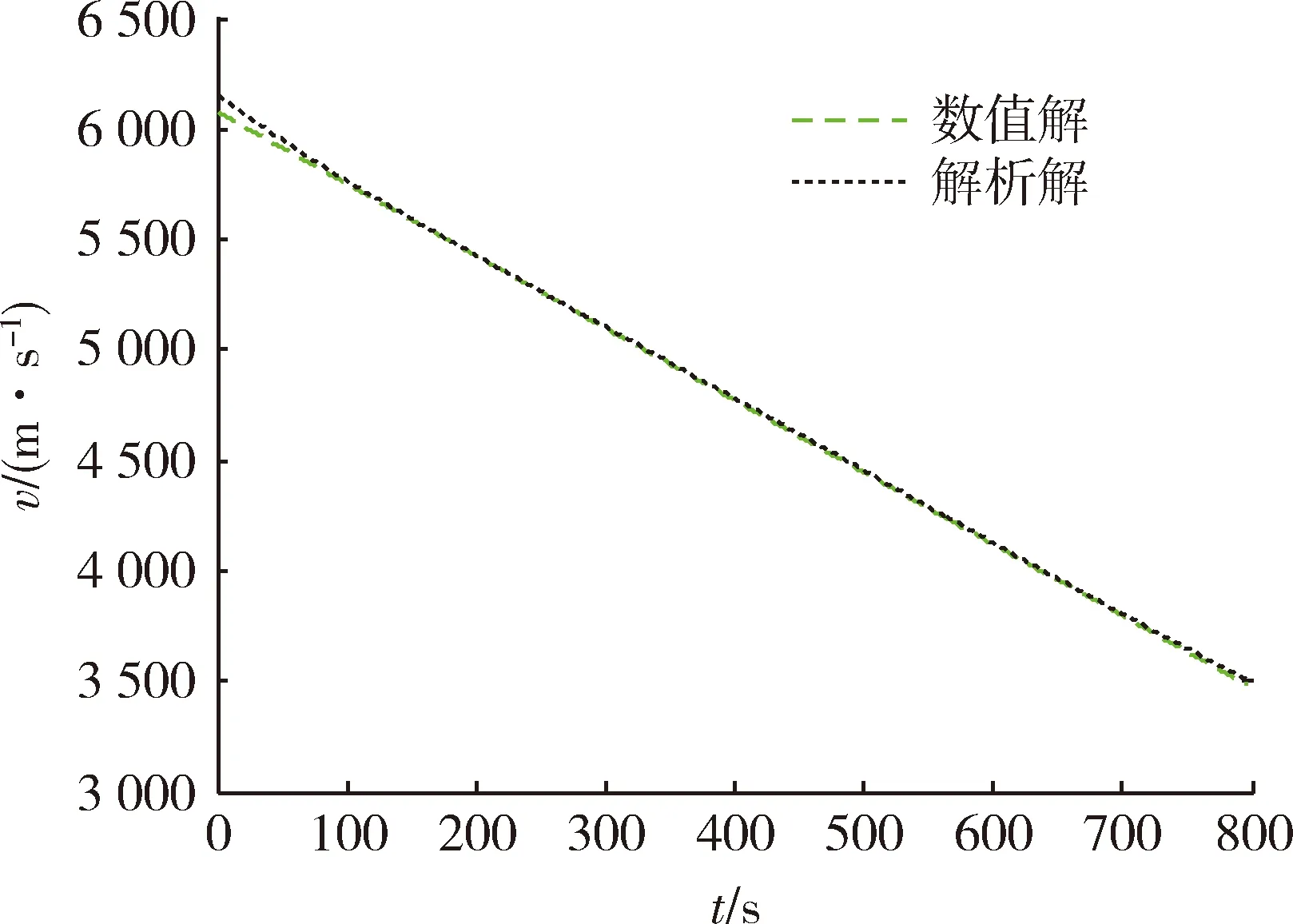
圖3 飛行速度數(shù)值解與解析解Fig.3 Numerical and analytical solution of flight speed

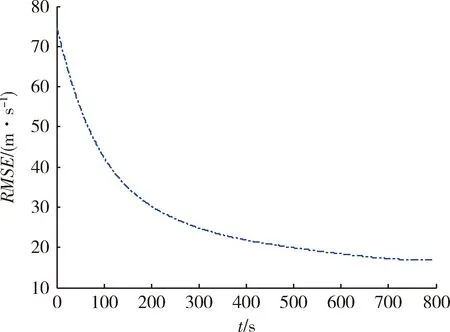
圖4 飛行速度解析解的RMSEFig.4 Analytical solution RMSE of flight speed

將速度傾角的三階近似解分別代入式(12)，(19)，(23)，可得到飛行速度、縱程及高度的解析解。圖3為飛行速度數(shù)值解與解析解，圖4為飛行速度解析解的RMSE。圖5為飛行縱程數(shù)值解與解析解，圖6為飛行縱程解析解的RMSE。圖7為飛行高度數(shù)值解與解析解，圖8為飛行高度解析解的RMSE。由圖4，6，8可知，飛行速度解析解的RMSE最大不超過80 m/s，在滑翔段結(jié)束時(shí)解析解的RMSE小于20 m/s；飛行縱程解析解的RMSE最大不超過140 km，在滑翔段結(jié)束時(shí)解析解的RMSE約為30 km；飛行高度解析解的RMSE最大不超過220 m，在滑翔段結(jié)束時(shí)解析解的RMSE小于50 m。由以上分析可知，飛行速度、縱程、高度的解析解均能以較高精度表征相應(yīng)狀態(tài)變量的數(shù)值解。

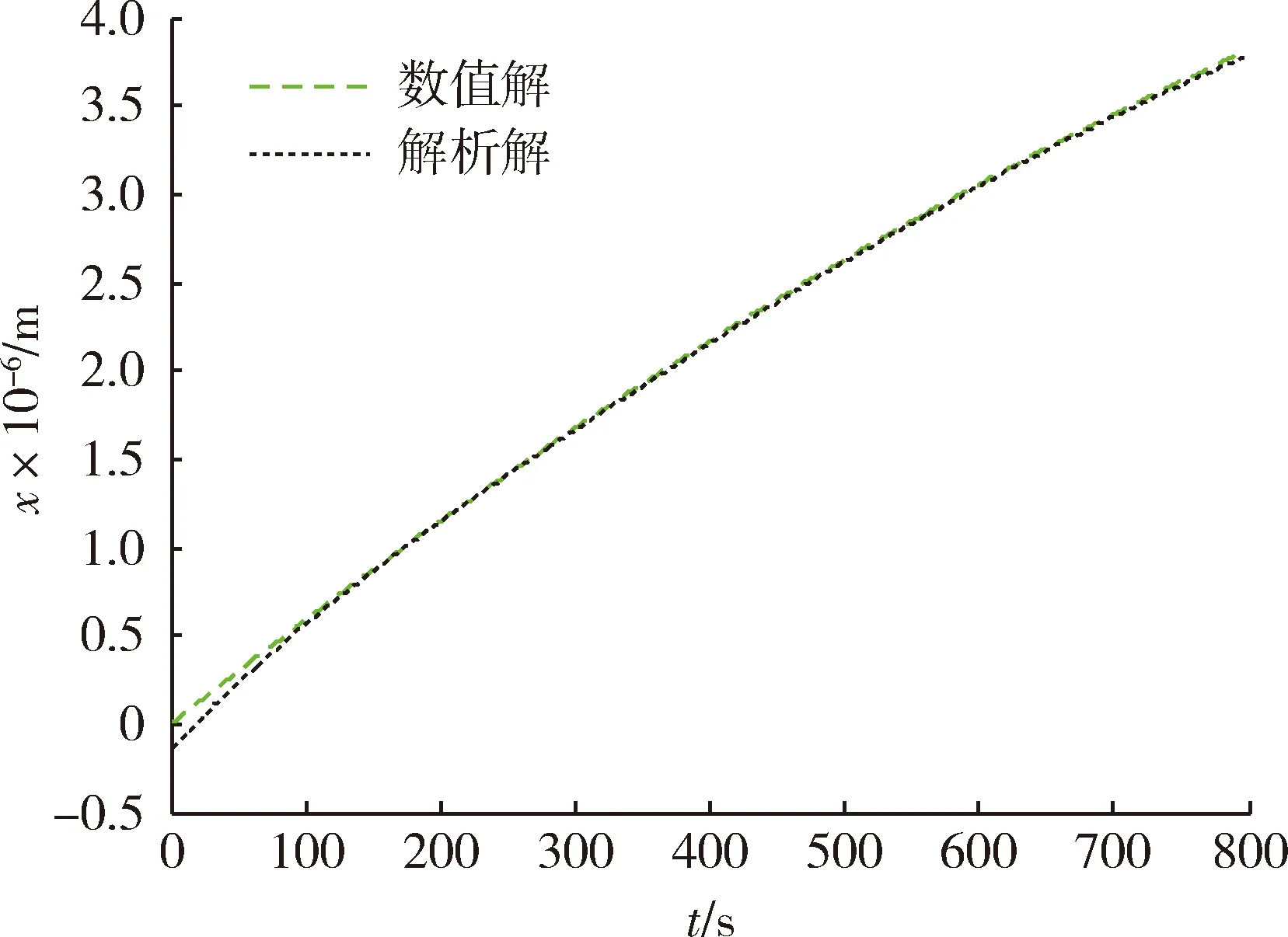
圖5 飛行縱程數(shù)值解與解析解Fig.5 Numerical and analytical solution of longitudinal range

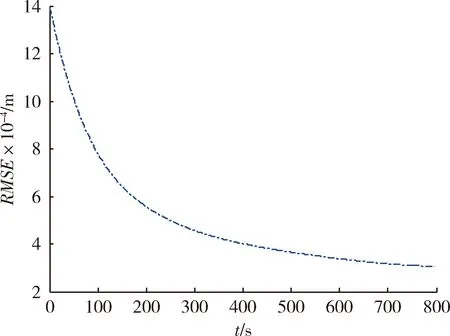
圖6 飛行縱程解析解的RMSEFig.6 Analytical solution RMSE of longitudinal range

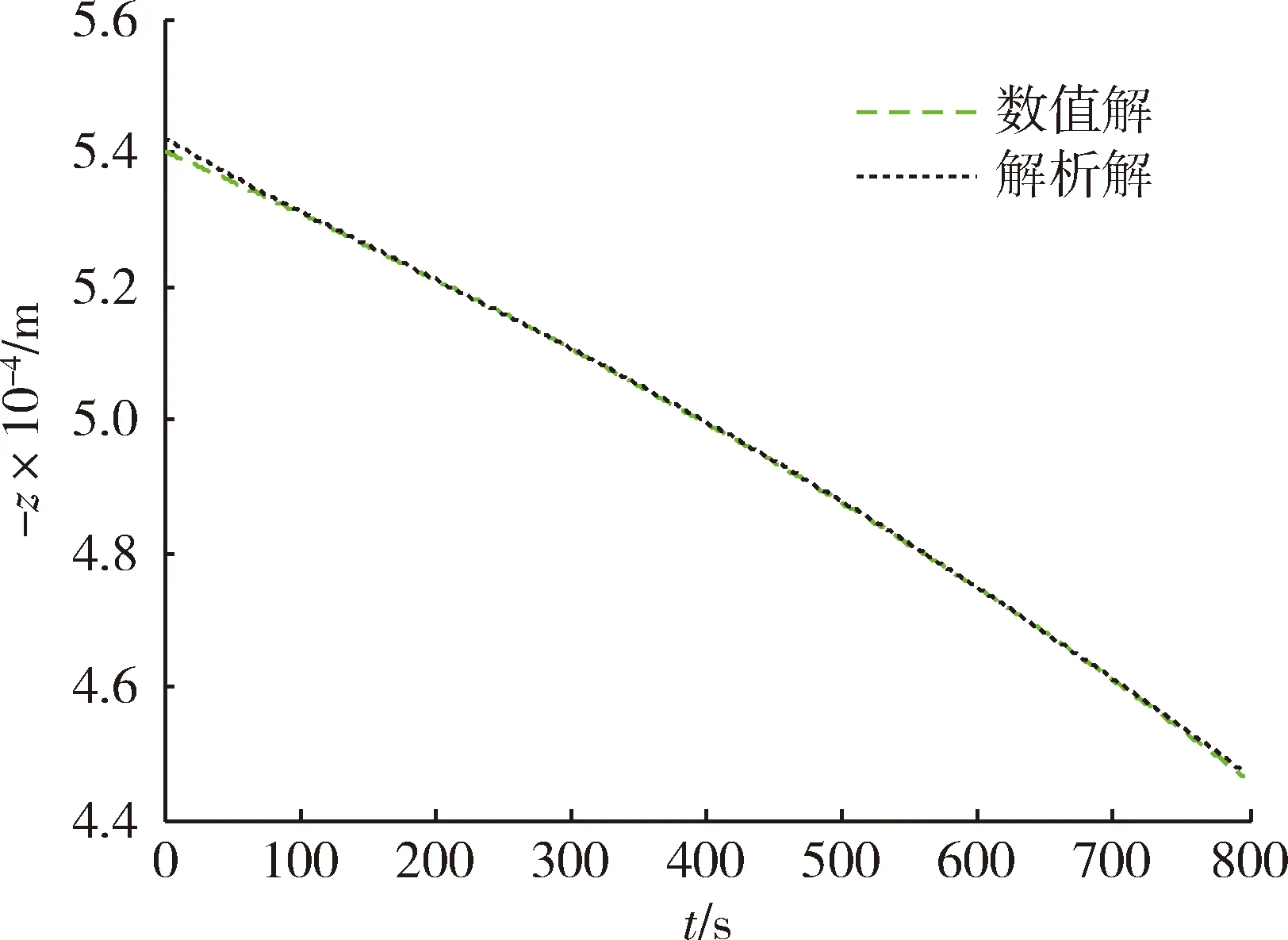
圖7 飛行高度數(shù)值解與解析解Fig.7 Numerical and analytical solution of flight altitude

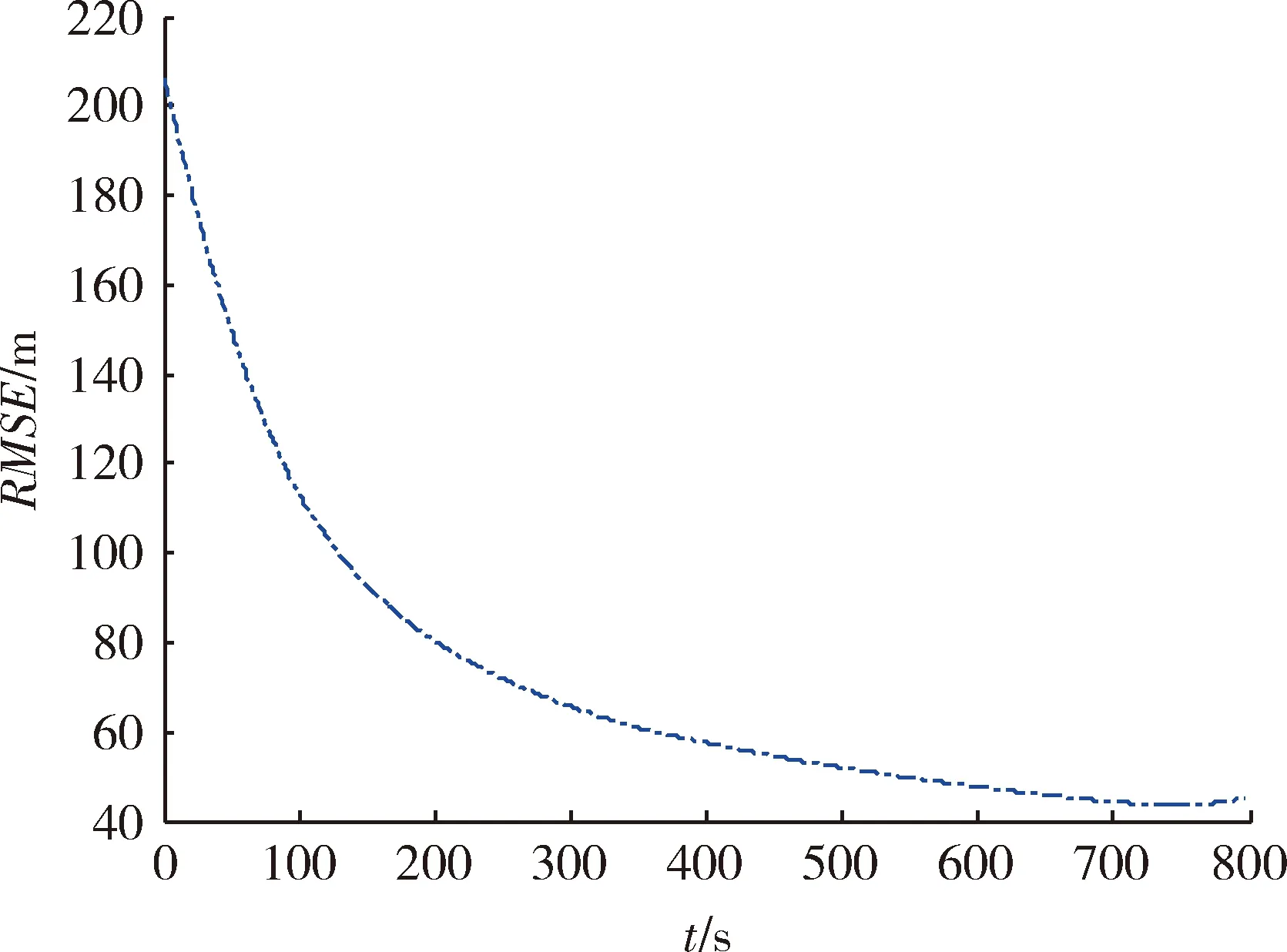
圖8 飛行高度解析解的RMSEFig.8 Analytical solution RMSE of flight altitude

4 結(jié)束語(yǔ)

針對(duì)高超聲速滑翔飛行器滑翔段狀態(tài)變量的求解問題，理論推導(dǎo)了平衡滑翔條件下飛行速度、飛行縱程、飛行高度的解析式，利用曲線擬合得到的速度傾角三階近似解的平均RMSE不大于0.003°。由仿真結(jié)果，可得到如下結(jié)論：

平衡滑翔條件下，速度傾角-飛行時(shí)間呈現(xiàn)非線性關(guān)系，利用二階或三階正交多項(xiàng)式均能很好的擬合速度傾角的數(shù)值解，三階近似解精度比二階近似解高0.001°左右。在得到速度傾角近似解的基礎(chǔ)上，飛行速度、飛行縱程和飛行高度的解析解都能以較高精度表征相應(yīng)狀態(tài)變量的數(shù)值解。在滑翔段結(jié)束時(shí)，飛行速度解析解的RMSE小于20 m/s，飛行縱程解析解的RMSE約為30 km，飛行高度解析解的RMSE小于50 m。