試飛階段軍用飛機任務可靠性增長建模及評估

高雅娟,馬濤,武紅姣

(中國飛行試驗研究院，陜西 西安 710089)

0 引言

可靠性是衡量飛機持續作戰能力的重要特性，對其進行科學、經濟、有效的評估與驗證具有重要意義。而軍用飛機的任務可靠性作為型號設計定型/鑒定試飛重要的評估驗證內容之一，對于裝備作戰適用性及作戰效能評估具有重要影響[1-2]。文獻[3-4]從工程應用的角度提出結合測試性驗證以及基于相似產品信息的任務可靠性評估方法。文獻[5]提出了基于飛行剖面的軍用飛機任務可靠性評估方法。文獻[6-7]考慮了環境、應力等因素對可靠性的影響，分別提出飛行參數折合系數法和基于比例風險模型的環境折合系數法。

根據文獻[8-9]，如果在設計定型試飛中安排專門的任務剖面進行試飛，則按照點估計進行評估;若定型試飛中未安排專門的任務剖面進行試飛，只是結合其他任務剖面進行評估時，則按照區間估計進行評估計算。由于目前，在型號設計定型/鑒定試飛中，一般不安排專項任務可靠性試飛剖面，只是結合性能試飛同步進行，一般采用文獻[10]中的點估計方法計算。

在軍用飛機及航空裝備設計定型/鑒定試飛期間，存在部分航空裝備早期故障并未完全排除，而是在試飛過程中“邊試驗、邊設計更改”，使得航空裝備的可靠性呈增長趨勢。文獻[11]提出復雜系統的壽命并不總是基于指數分布的，應該基于數據檢驗來確定其分布形式。如果不考慮可靠性增長的因素，則其評估結果無法反映試飛結束時任務可靠性的真實水平。

本文考慮設計定型/鑒定試飛期間軍用飛機可靠性增長的現象，分析研究廣義Gamma分布曲線特點及其與試飛階段軍用飛機可靠性增長現象的符合性的前提下，提出基于Gamma分布的軍用飛機任務可靠性評估模型，并以某型飛機的試飛數據為例，給出該方法的應用示例。

1 可靠性增長理論模型

文獻[12]中介紹了幾種常用的可靠性增長模型，主要包括AMSAA模型，Duane模型以及Weibull分布等。在具體的工程應用中，AMSAA模型由于約束條件太多且對數據的規律性要求較高，限制其在工程中的應用;而Duane模型則無法給出可靠性的區間估計結果;在Weibull分布中,由于其形狀參數的變化，對于故障率遞增、遞減及不變的情況都有較好的適應性。但是Weibull分布參數的極大似然估計變化呈現不規范性，即使在位置參數為0，且在形狀參數大于1時，Weibull分布的故障率從0遞增到無窮大，這與工程實際表現出了不相符性。

而Gamma分布故障率曲線較特殊，類似于Weibull分布，且其故障率曲線單調性只與形狀參數有關，且不論是單調遞增或是遞減，Gamma分布的故障率始終有界。文獻[13-14]對幾種Gamma分布及其與指數分布、威布爾分布進行了對比。Gamma分布的密度函數為

(1)

式中：k為形狀參數；θ為尺度參數，取θ=1。

利用E.Glaser準則，其失效率函數為

(2)

當k>1，λ(t)單調遞增，失效率增加，可靠性處于下降過程；當k=1，λ(t)為定值，Gamma分布退化為指數分布，失效率為常數即可靠性不變；當k<1，λ(t)單調遞減，失效率減小，可靠性處于增長過程。

由圖1可以看出，與Weibull分布不同，Gamma分布的故障率是有界的，且當k<1時，和浴盆曲線的早期故障階段到偶然故障階段的過渡相似。因此，Gamma分布可以很好地描繪可靠性增長的過程中，故障率逐漸降低，最后趨于穩定值的過程。正是由于Gamma分布的這種特性，文獻[15-16]提出將廣義Gamma分布用于可靠性評估。

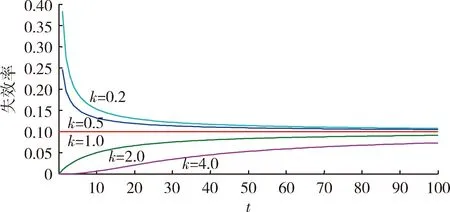
圖1 Gamma分布失效率Fig.1 Failure rate of Gamma distribution

2 基于Gamma分布的任務可靠性增長評估模型

鑒于Gamma分布的特點，可利用其將變母體的可靠性增長數據有效地利用起來，評估最終飛機裝備的任務可靠度,文獻[17-18]給出了Gamma分布參數的估計方法。由于傳統的Gamma分布參數的極大似然估計很難求解，本文引入廣義Gamma分布，其概率密度函數為

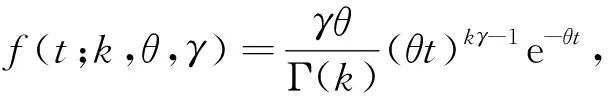
(3)

式中:γ為位置參數。顯然，當γ=1時，廣義Gamma分布和Gamma分布相同。其似然方程組為

(4)

解上面的方程組即可得到Gamma分布的極大似然估計為

(5)

(6)

(7)

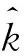
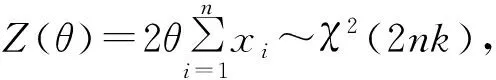
3 基于Gamma分布的某型軍用飛機任務可靠性評估

3.1 數據預處理

基于Gamma分布模型的任務可靠性增長評估結果的準確性，主要受到任務成功判據的合理性以及數據收集的準確性的影響。在任務可靠性評估時，故障收集的對象為“會導致飛機任務失敗的故障”，主要包括：

(1) 導致飛機延誤或取消飛行；

(2) 提前返航或提前著陸；

(3) 任務中斷或被迫改變飛行任務；

(4) 導致任務失敗或等級事故。

下述情況不計入影響飛機任務可靠性的故障統計次數：

(1) 在執行任務過程中，有余度的系統或設備中的單臺發生故障，或與執行本次任務不直接相關的設備或系統發生故障；

(2) 非設備故障所致的任務降級或任務失敗。

依據以上任務可靠性評估數據收集及評判原則，對某型軍用飛機設計定型試飛期間的數據進行統計。在該評估周期內，某型軍用飛機共發生3次故障，分別為200X年X月X1日的2起故障和200X年X月X2日的1起故障。將200X年X月X1日的2個故障拆開，取當天任務時間為這2個相鄰故障的間隔時間；第3個故障后的幾次試飛未發生故障，則該段時間取為截尾時間；得到故障間隔時間數據如表1所示。

表1 故障間隔時間Table 1 Time Between Failure h

由于觀測到的故障較少，且包含1個截尾數據，因此區間估計不采用極大似然估計，而采用填充數據的方法，設最后一個故障間隔時間為以參數估計值為真值的條件分布的期望。

設Z=(z1,z2,…zn-r)為未觀測到的失效時間，T=(t1,t2,…tr)為所有觀測到失效時間。ρ=(k,θ)，ρ(i)=(k(i),θ(i))為第i次迭代結果。Z服從條件分布，Z～P(Z≤z|Z>tr)。

首先求期望：

(8)

L(T,Z|ρ)=lgp(T,Z|ρ)為完全數據情況下的對數似然函數。給定第i次迭代后的參數估計值ρ(i)，則對Z取條件期望，得到結果：

Q(i)=n(klgθ-lg Γ(k))+

(n-r)(k-1)EZ(lgZ|ρ(i),T)-

(n-r)EZ(Z|ρ(i),T).

(9)

EZ(lgZ|ρ(i),T)和EZ(Z|ρ(i),T)均為無窮積分，且較難計算，因此可采用Monte Carlo模擬得到二者的近似值。

對期望最大化：

(10)

得到

(11)

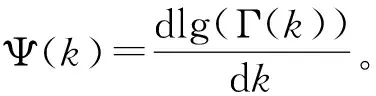
不斷重復以上過程，直至最終滿足|k(i+1)-k(i)|<ε或|θ(i+1)-θ(i)|<ε，ε為絕對誤差限。但是考慮到求期望過程中采用的模擬近似存在一定的波動性，可以對連續多個k(i)值取平均，隔幾次迭代后，再對多個k(i)值取平均，比較2次均值的差是否在誤差限ε內。為減少收斂時間并考慮模擬期望的波動性，ε可選取稍大一點的值，如取ε=0.05。

3.2 計算過程

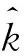
(12)

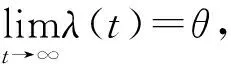
3.3 計算結果

根據以上計算方法，可得某型軍用飛機基于Gamma分布的任務可靠性評估結果，且該結果可反映本階段試飛結束時，該型軍用飛機任務可靠性增長后達到的水平。表2給出了某型軍用飛機對應不同置信度的任務可靠度下限評估結果。

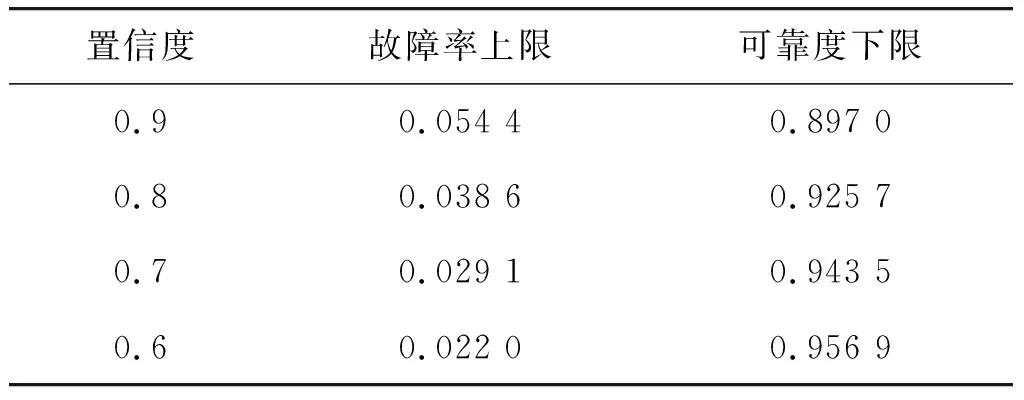
表2 Gamma分布方法的故障率上限和可靠度下限Table 2 Upper limit of failure rate & lower limit of reliability based on gamma distribution

4 結束語

本文通過對幾種常用的可靠性增長評估模型的適用性的分析，利用Gamma分布對于設計定型試飛期間，軍用飛機的失效率從浴盆曲線的早期故障階段過渡到偶發故障階段這一過程的良好符合性及分布的有界性，建立基于Gamma分布的軍用飛機任務可靠性增長評估模型，并以某型軍用飛機的任務可靠性評估為例，對該方法的工程適用性進行驗證，結果表明：該方法可用于試飛階段軍用飛機任務可靠性增長評估。