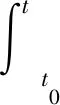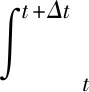一類線性隨機時變系統的采樣控制
劉厚良,吳小太
(安徽工程大學 數理金融學院,安徽 蕪湖 241000)
時變系統在自然界與工程界中廣泛存在,需要建立時變的系統模型,并分析其性質特征。時變系統的穩定性研究受到了專家學者們的廣泛關注。由于系統的時變特征導致現有文獻中時不變系統穩定性的相關研究方法不能被應用到時變系統上來,這給時變系統穩定性的研究帶來了極大的挑戰。近年來,線性時變系統的穩定性與穩定化研究取得了一定的進展,例如:Zhou[1]給出了線性時變系統漸近穩定性、指數穩定性和一致指數穩定性的充要條件。Yu[2]等總結了研究時變系統的幾個關鍵問題,隨后給出了兩種不同的時變系統模型描述方法并分析討論了不同的時變系統控制方法,最后就時變系統研究趨勢及核心問題探討了時變系統控制問題的研究方向。Date[3]等研究了一類線性時變控制系統,并且給出了一種設計線性狀態反饋控制器和Luenberger觀測器的方法。Zhou[4]等在Razumikhin定理和Krasovskii定理條件下對時變時滯系統進行穩定性分析,并推廣了經典Razumikhin和Krasovskii條件下時滯系統的穩定性定理。
由于對系統的所有狀態進行連續時間的觀測反饋非常困難,近年來離散時間的反饋控制受到了廣大學者們的重視。例如:Krishnasamy[5]等在Wirtinger不等式的基礎上,構造分段Lyapunov-Krasovskyii泛函,研究了基于采樣-數據控制的切換中立型系統的鎮定問題。Briat[6]將確定性脈沖系統的結論推廣到隨機集上,利用駐留時間的工具給出了系統的穩定性條件,并將所得結果應用于隨機采樣數據系統的分析與控制。Wang[7]等通過構造一類分段Lyapunov-Krasovskii泛函,解決了基于狀態量化的采樣數據神經網絡系統的鎮定問題。Zhao[8]等研究了具有異步切換與量化輸入的切換中立系統的采樣控制問題,并最終設計了一種基于采樣數據的具有傳輸延遲的控制器。Zhang[9]等研究了一類線性時變系統的采樣數據控制問題,首先將Halanay不等式擴展到時變采樣數據系統,然后基于比較原理和擴展的Halanay不等式,給出了相應閉環系統的全局一致指數穩定性和全局一致漸近穩定性的新判據,接著提出了一種求解增益矩陣問題的算法,最終給出了一個例子以證明所得到結果的有效性。
在現實中系統往往會受到隨機因素的干擾,需要建立隨機微分系統對隨機擾動進行建模分析。例如:Wu[10]等研究了具有時變時滯的切換隨機神經網絡的全局指數穩定性。利用數學歸納法、分段李雅普諾夫函數和平均駐留時間方法研究了具有穩定子系統的切換隨機時滯神經網絡的穩定性。Florchinger[11]利用LaSalle不變性原理,設計出隨時間變化的反饋定律,證明了系統依概率漸近穩定。
綜上所述,雖然對于連續時間系統采樣控制的研究取得了豐富的成果,但對于隨機時變系統采樣控制的研究仍需進一步完善。文獻[9]對確定性時變系統的采樣控制問題進行了深入地探討,而對隨機時變系統的采樣控制問題有待于進一步去探索。同時,文獻[9]中的方法并不能被直接應用到隨機時變系統的采樣控制研究。對于隨機時變系統的采樣控制,需要使用隨機分析的方法進行研究,其分析方法遠比確定性系統復雜。因此,研究了一類線性時變系統的采樣控制問題,相關理論結果可以拓廣文獻[9]的部分結論。
1 模型構建
研究如下線性隨機時變微分系統:
dx(t)=[A(t)x(t)+B(t)u(t)]dt+C(t)x(t)dW(t)。
(1)
式中,x(t)∈Rn為系統的狀態向量;A(t)∈Rn×n以及B(t)∈Rn×m為時變矩陣;W(t)是一個標準的布朗運動;u(t)∈Rm為控制輸入;記系統初值x(t0)?x(0)。假定采樣控制器滿足
u(t)=K(tk)x(tk),t∈[tk,tk+1)。
(2)
式中,K(tk)為控制增益矩陣。樣本序列tk(k=0,1,2,…)滿足t0 將系統(2)代入系統(1),可得到如下離散時間采樣的閉環系統: dx(t)=[A(t)x(t)+B(t)K(tk)x(tk)]dt+C(t)x(t)dB(t)。 (3) 下面將對系統(3)的穩定性進行討論。在此之前,需要一些相關定義。對于每一個V∈C1,2,針對系統(1),定義算子LV:[t0,∞)×Rn。 LV(t,x(t))=Vt(t,x(t))+Vx(t,x(t))[A(t)x(t)+B(t)u(t)]+ (4) 在證明主要結論前需要給出一些相關定義和引理。 定義1[9]假定函數β(·,·)為KL函數,對于?t≥t0滿足 ‖x(t)‖≤β(‖x(t0)‖,t-t0), 則稱系統(2)滿足全局一致漸近穩定性。進一步,如果存在兩個正常數M0和α滿足 ‖x(t)‖≤M0e-α(t-t0), 則稱系統(3)滿足全局一致指數穩定性。 引理1[9]若l(t)為[t0,+∞)上的全局一致穩定函數,則存在3個非負常數c,d與T,使得對?t≥t0有 (5) 假設1 對于線性隨機時變系統(3),存在可導對稱矩陣值函數P(t),全局一致穩定函數l(t)以及一個常量0≤p1≤p2滿足 (6) 和 p1In≤P(t)≤p2In。 (7) (8) 證明由常數變易法可知: 下面將使用引理2來研究線性時變系統的穩定性。 定理1 設l(t),h(t)為[t0,+∞)上的連續函數,|l(t)|≤γ。若存在函數y(t)∈R+滿足 y(t)≤l(t)y(t)+h(t)y(tk),t∈[tk,tk+1)。 (9) 記 ②若u(t)為全局一致穩定函數,則 這里c,d為非負常數,如引理1定義。 證明首先,構造方程 (10) 這里y1(tk)=y(tk),k∈N。注意到系統(9)與系統(10)的形式,由比較定理可得: y(t)≤y1(t)。 (11) 此時根據引理2可得: 也即 (12) 由式(12)有 (13) 與 (14) 將式(14)代入(13)可得: (15) (16) 結合式(11),有 (17) 由式(12),有 (18) 以及 (19) 推論1 設l(t),h(t)為[t0,+∞)上的連續函數,|l(t)|≤γ。若存在函數y(t)∈R+滿足 (20) 記 ②若u(t)為全局一致穩定函數,則存在常數c,d使得 證明注意到ln(1+x)≤x,對于x>0,可得: ln(1+ak) (21) (22) 同理,由定理1的證明可知推論1成立。 注1:由推論1可知,定理1拓廣了文獻[9]中定理1的假定條件,可以有效降低文獻[9]中結論的保守性。 定理2 在假設1成立的條件下, ①存在一個正常量η使得: ②若存在一個正常數η使得l(t)+η+h(t)e(γ+η)h為全局一致穩定函數,則系統(3)滿足全局一致指數穩定。 證明①對于系統(3),由依藤公式可得: (23) 對上式兩邊同時取期望可得: (24) 于是,對于t,t+Δt∈(tk,tk+1),有 (25) 注意到LV(x,x(t))的連續性,可得: ELV(t,x(t)),t∈[tk,tk+1)。 (26) 假定V(t,x(t))=xT(t)P(t)x(t),t∈[tk,tk+1)。注意到xT(t)cT(t)P(t)c(t)x(t)是一維變量,由于 LV(t,x(t))=Vt(t,x(t))+Vx(t,x(t))((A(t)x(t)+B(t)K(tk)x(tk))+ xT(t)cT(t)P(t)c(t)x(t), 代入可得: xT(tk)KT(tk)BT(t)P(t)x(t)+xT(t)P(t)B(t)K(tk)x(tk)≤l(t)V(t,x(t))+ (27) 有 由定理1可知系統(3)滿足全局一致穩定。 ②參考定理2的證明可以很容易得出該結論。 注2:根據文中定理2的結論,結合文獻[9]中的時變系統采樣控制器設置的方法,可以類似給出相應系統(3)的采樣控制器。由于文章篇幅有限,不再對控制器的設置進行贅述。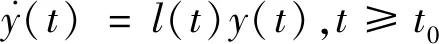
2 主要結果