奇妙的三階幻方

【例1】在下圖的3×3陣列中填入了1～9的自然數，構成了大家熟悉的三階幻方。

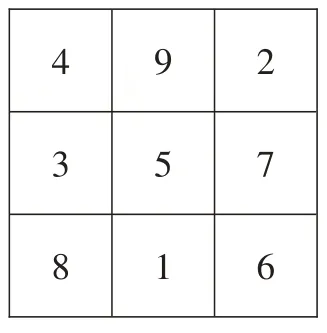
現在另有一個3×3的陣列，請選擇九個不同的自然數填入九個方格中，使其中最大者為20，最小者大于5，且每行、每列及每條對角線上的三個數的和都相等。

【思路點睛】最基本的三階幻方中，填入的是1～9 這九個不同的自然數，其中最大的為9，最小的為1。要使新編制的幻方中最大數為20，而9+11=20，因此，如果在所給幻方中各數都增加11，就能構成一個新幻方，并且滿足最大數為20，最小數大于5。如下圖：

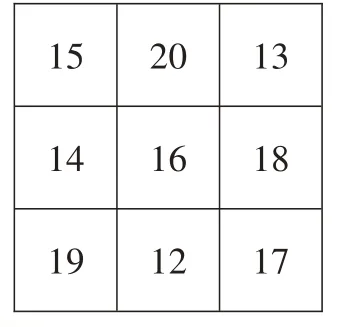
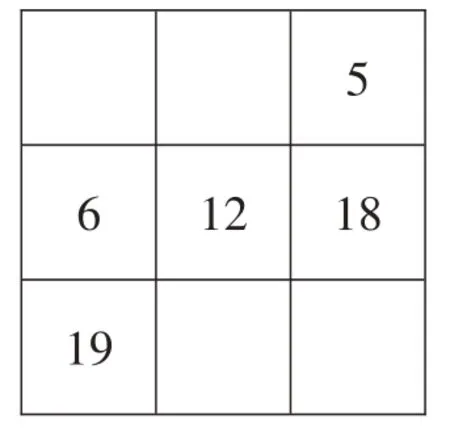
【例2】在3×3 的陣列中，第一行第三列的位置上填5，第二行第一列的位置上填6，如下圖。請你在其他方格中填上適當的數，使方陣橫、縱、斜三個方向的三個數之和為36。

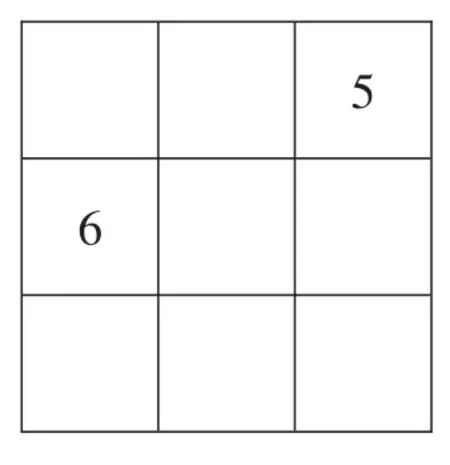
【思路點睛】因為三個數的和是36，所以可求出三個數的平均數是36÷3=12，這個12也就是中心數，即填在幻方中間的數。

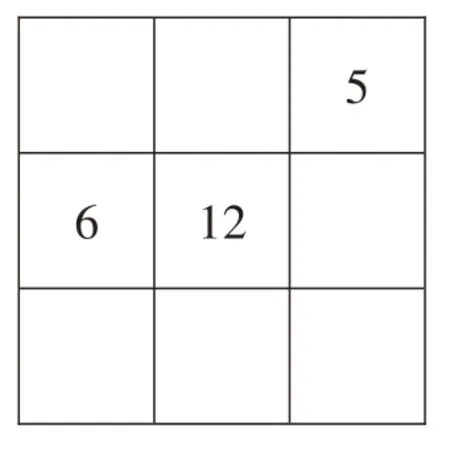
填出了中間數，那么第二行右邊的數就是36-12-6=18；對角線左下角的數是36-12-5=19。

得到了這兩個數，剩下的就好辦了。用36減去已知數，得到剩下的數：

36-19-6=11；36-18-5=13；36-11-5=20；36-19-13=4。

從上面的例題我們不難看出：要填出一個三階幻方，中心數起著至關重要的作用。利用“三個數的和=中心數×3”這個關系式，在已知和的情況下，可先求出中心數；在得到中心數的情況下，利用三個數的和，求出其他數。