一種用于求解TSP問題的隨機最佳插入煙花算法 *
吳俊斌,吳 晟,吳興蛟
(1.昆明理工大學信息工程與自動化學院,云南 昆明650500;2.華東師范大學計算機科學與技術學院,上海 200062)
1 引言
旅行商問題TSP(Traveling Salesman Problem)自1959年提出已經過去了半個多世紀, TSP問題是一個NP難問題[1-3],目前為止都沒有一種高效且精準地求解方法。高效精準地求解TSP問題在車輛路徑規(guī)劃、O2O物流配送等很多領域都有著非常重要的意義。TSP問題的目標是在一系列點集中尋找一條最短回路,并要求每個點只訪問一次,目前主要的求解方法為啟發(fā)式智能算法,如遺傳算法、蟻群算法和蝙蝠算法等。近幾年,很多學者致力于研究現(xiàn)代啟發(fā)式智能算法及其優(yōu)化算法,如張瑾等人[4]提出的離散蝙蝠算法以及袁汪凰等人[5]提出的自適應模擬退火蟻群算法。
煙花算法FWA(FireWorks Algorithm)[6]2010年由Tan等人提出,是一種模擬煙花爆炸產生火花以照亮夜空的現(xiàn)象探索鄰域的群體智能優(yōu)化算法。在求解復雜的優(yōu)化問題時,該算法不僅具有較強的局部搜索能力,同時還保留了良好的全局搜索能力。近年來煙花算法受到廣大學者的關注,并被成功運用到許多領域,如Web服務組合優(yōu)化[7]、智能診斷齒輪箱故障[8]、多維背包[9]、多無人機任務分配[10]和作業(yè)車間調度[11,12]等,各項研究表明煙花算法具有較好的收斂性和穩(wěn)定性[13]。
本文針對TSP問題的特點,考慮煙花算法的尋優(yōu)機制,設計了一種基于隨機最佳插入的煙花算法RBIFWA(Randomized Best Insertion FireWorks Algorithm)。該算法改進了傳統(tǒng)煙花算法爆炸資源的分配方式,創(chuàng)新性地提出了2個全新算子:拋棄節(jié)點重新插入的爆炸算子和拋棄路徑重新插入的變異算子。然后通過精英與輪盤賭相結合的選擇策略對煙花進行選擇,能夠很好地求解TSP問題。算法基本思想如下:初始生成的煙花為TSP問題的一條完整路徑,煙花爆炸產生的火花為原有煙花在鄰域搜索得到的一條新的路徑,質量較優(yōu)的煙花爆炸產生的火花數(shù)量較多,但爆炸半徑較小,即其局部搜索的能力較強;質量較差的煙花爆炸半徑較大,但火花數(shù)量較少,即其可提高算法全局搜索能力。煙花質量的優(yōu)良由適應度值決定,根據(jù)適應度分配煙花資源,有效平衡了算法全局和局部的搜索能力[14]。為驗證算法的有效性,最后使用TSPLIB標準庫進行測試,并與基本煙花算法、混沌煙花算法CFWA(Chaotic FireWorks Algorithm)[15]、離散蝙蝠算法DBA(Discrete Bat Algorithm)[4]和自適應模擬退火蟻群算法SA-MMAS(Simulated Annealing Max-Min Ant System)[5]進行比較。
2 TSP問題模型
TSP問題可描述為:由n個點構成的點集V={v1,v2,…,vn}表示n個城市的集合,一個商品推銷員需到這n個城市推銷商品,要求從某一城市出發(fā),剩余的n-1個城市必須且僅能經過1次,最后回到出發(fā)城市,若已知每對城市之間的距離,求如何安排各城市的訪問次序才能獲得最短的路徑。
假設d(vi,vj)表示城市vi到城市vj的距離,i,j∈{1,…,n},該商品推銷員訪問城市的次序為p={v[1],v[2],…,v[n],v[1]},其中v[i]∈V表示訪問的第i個城市,則這條路徑的長度為:
(1)
若D(p)的值最小,則由p構成的路徑為該TSP問題的最優(yōu)解。
3 改進型隨機最佳插入算法
隨機最佳插入RBI(Randomized Best Insertion)是一種隨機性啟發(fā)式算法,該算法實現(xiàn)簡單,并能有效平衡精度和計算性能,常用于快速構建一個次優(yōu)解。然而實驗發(fā)現(xiàn),RBI算法在求解TSP問題時很容易將距離較遠的點優(yōu)先插入,造成交叉路徑,使解的質量降低。考慮到最優(yōu)TSP路徑的相鄰節(jié)點均是距離較近的幾個節(jié)點[16],本文對RBI算法進行了改進,描述如下:
假設p(t)是算法在第t次迭代時的部分TSP封閉路徑:
p(t)={v[1],v[2],…,v[t],v[1]}
(2)
W(t)=V-p(t)為第t次迭代時尚未訪問的節(jié)點的集合,其中V={v1,v2,…,vn}為TSP所有節(jié)點的集合,|W(t)|=n-t為第t次迭代尚未訪問的節(jié)點數(shù)量。
定義vc為p(t)的幾何中心,wi(wi∈W(t))與vc的距離可以表示為式(3)所示:
dc(wi)=d(wi,vc)
(3)
定義wi在p(t)中的最佳位置滿足式(4):
(4)
其中,wi∈W(t),Δd[j](wi)滿足式(5),表示將wi插入到p(t)第j個位置所增加的長度。
Δd[j](wi)=d(v[j-1],wi)+
d(wi,v[j])-d(v[j-1],v[j])
(5)
通過改進RBI算法構建TSP路徑的算法如算法1所示。
算法1改進RBI算法
輸入:V={v1,v2,…,vn}。//TSP所有節(jié)點的集合
輸出:p={v[1],v[2],…,v[n],v[1]}。//一條完整路徑
t←1;
隨機選擇v[1]∈V;
初始化路徑p(t)={v[1],v[1]};
初始化W(t)←V-p(t);
While|W(t)|≠0Do
計算p(t)的幾何中心vc;
通過式(3)計算W(t)中各點wi距幾何中心vc的距離dc(wi);
從W(t)中找出dc(wi)最小的r個點,構成Wr(t)={w[1],w[2],…,w[r]};
隨機選擇w∈Wr(t);
通過式(4)找到w的最佳插入位置;
將w插入到p(t)的最佳位置;
將w從W(t)中刪除;
t←t-1;
EndWhile
其中,r=min(n-r,R),R為隨機因子,R越小越接近貪心策略,使每次插入的節(jié)點都是p(t)附近的幾個節(jié)點,R越大越能提高解的多樣性。通過與原RBI算法進行對比發(fā)現(xiàn),當R選擇合適數(shù)值時可以抑制交叉路徑的產生,提高解的質量,同時又能保證解的多樣性。
4 改進型煙花算法
煙花算法主要由初始煙花、爆炸算子、變異算子和選擇策略4部分組成[17]。本文針對TSP問題的離散特性,改進了爆炸資源分配的方式,創(chuàng)新性地提出了拋棄節(jié)點重新插入的爆炸算子和拋棄路徑重新插入的變異算子,然后通過精英與輪盤賭相結合的煙花選擇策略,能夠很好地求解TSP問題。其中,煙花和火花對應TSP中的一條完整路徑,初始煙花由改進RBI算法隨機產生,共計得到M個初始煙花;爆炸算子和變異算子用于搜索,并得到新的火花;選擇策略將對煙花進行篩選,以進行下一次迭代。改進的煙花算法流程如圖1所示。
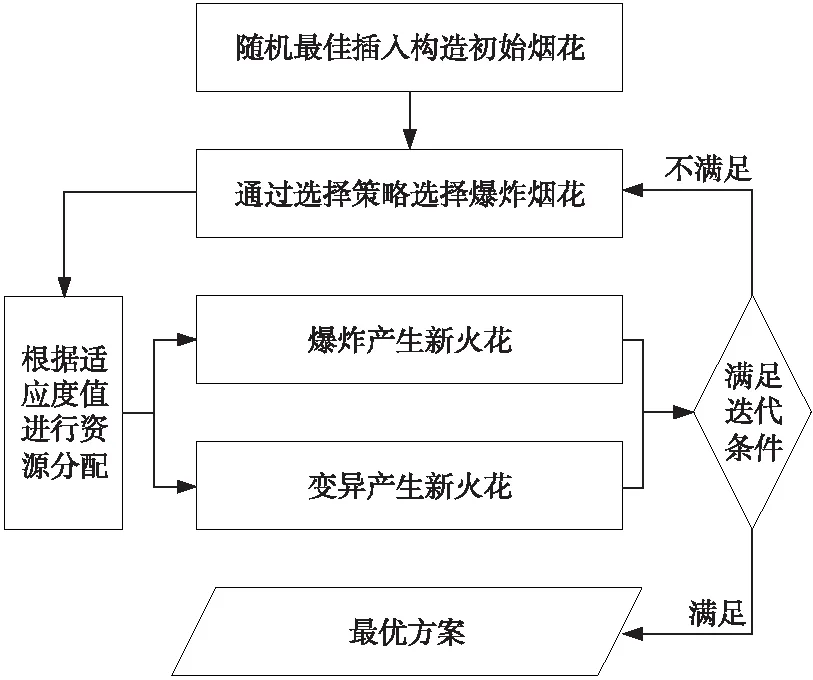
Figure 1 Flowchart of improved fireworks algorithm圖1 改進的煙花算法流程示意圖
4.1 適應度評估函數(shù)
適應度評估函數(shù)用于評估解的優(yōu)劣程度,適應度值[18]越小,則表示適應度較優(yōu),解的質量較高;適應度值越大,則表示適應度較差,解的質量較低。
設一條完整的TSP路徑為一個有效解,路徑訪問節(jié)點的順序為pi={v[1],v[2],…,v[n],v[1]},則定義這條路徑的適應度值如式(6)所示:
f(pi)=D(pi)=
(6)
即TSP路徑的適應度值為這條路徑的總長度,由此可知,最短的TSP路徑有最優(yōu)的適應度值。
4.2 爆炸資源分配
煙花算法的基本思想如下:煙花為解空間中的部分可行解,煙花爆炸產生的火花會照亮周圍的夜空,其中周圍夜空表示鄰域解構成的空間,其大小由爆炸半徑來度量,爆炸產生的火花為煙花在鄰域空間中搜索的新解。圖2所示為實際煙花爆炸與煙花算法的類比。

Figure 2 Analogy of the fireworks explosion and fireworks algorithm圖2 實際煙花爆炸與煙花算法的類比圖
煙花爆炸的資源分配遵循一個共同的原則,即適應度值較優(yōu)的煙花能夠產生更多的火花,爆炸的半徑較小,適應度值較差的煙花能夠產生較少的火花,但爆炸半徑更大[19]。根據(jù)這一原則,在爆炸前需要根據(jù)適應度計算各煙花的爆炸半徑和爆炸產生火花的數(shù)量,選擇m個煙花作為煙花種群參與爆炸,計算方法如式(7)和式(8)所示:
(7)
(8)
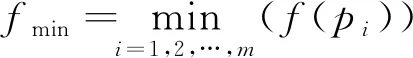
本文針對TSP的特征,經過多次實驗,設計了求解A和S的方法,如式(9)和式(10)所示:
(9)
S=m·k
(10)
其中,m為參與爆炸的煙花數(shù)量,n為TSP的節(jié)點數(shù),n/l和k為煙花的平均爆炸半徑和平均爆炸數(shù)量。在這個問題中,l∈[2,3],k∈[10,20]。當n較小時,適當增大l并減小k可以提高算法局部搜索能力,使得算法更快收斂;當n較大時,適當減小l并增大k可以提高算法全局搜索能力,有利于跳出局部最優(yōu)解。
由于TSP問題離散的性質,一般期望處理結果是一個整數(shù),然而式(7)和式(8)得到的是一個實數(shù)。同時為避免求得的爆炸半徑或產生的火花數(shù)量過大或過小,可以通過式(11)和式(12)將得到的實數(shù)轉換為整數(shù),并將其控制在一定范圍內。

(11)
(12)
其中,Amax,Amin,Smax,Smin皆為預設的整數(shù)常數(shù),代表爆炸半徑的最大值和最小值及爆炸火花數(shù)量的最大值和最小值。
4.3 爆炸算子
當煙花獲得爆炸資源A和S后,將在周圍發(fā)生爆炸,產生一組新的火花,用于探索鄰域解。為了更好地探索鄰域解,本文設計了一種新穎的爆炸操作算子。

提示:(1)根據(jù)氧化還原反應的規(guī)律,次氯酸鈣與濃鹽酸反應生成氯化鈣、氯氣與水,反應的化學方程式為Ca(ClO)2+4HCl(濃)==CaCl2+2Cl2↑+2H2O。
當產生的火花優(yōu)于原煙花時,則接收該解,并將該火花加入煙花種群中,以供下次迭代時選擇;當產生的火花與原煙花相同時,則拋棄該火花;當產生的火花劣于原煙花時,則以一定概率接收較差的解,接收概率如式(13)所示:
(13)
其中,fin為原煙花的適應度值,fout為產生的火花的適應度值,θ為控制參數(shù),取[1,2]較為合適。由此可知,適應度越接近原煙花的火花,被接收的概率越大。為描述方便,本文將被接收的火花稱為有效火花,被拋棄的火花稱為無效火花。有效煙花構成的集合稱為煙花種群。
4.4 變異算子
變異算子與爆炸算子不同,能夠增加煙花種群的多樣性,一定程度上能夠跳出局部最優(yōu)解,探索更優(yōu)解。針對TSP問題,本文設計了一種合適的變異操作算子。
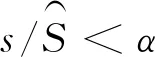
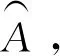

(14)
其中,xmin為允許變異刪除的最小連續(xù)節(jié)點數(shù),xmax為允許變異刪除的最大連續(xù)節(jié)點數(shù),C為迭代總次數(shù),c為當前迭代的次數(shù)。
4.5 選擇策略
隨著煙花種群數(shù)量的增加,如何選擇煙花參與下一次爆炸顯得至關重要。為此本文使用精英選擇與輪盤賭相結合的選擇策略。假設要從種群中挑選m個煙花參與下一次爆炸,那么種群中的最優(yōu)個體將被確定性地選擇,剩余m-1個煙花則通過輪盤賭的方式從種群中進行選擇。對于煙花種群中的每一個煙花pi,其被選擇的概率如式(15)所示:
(15)
其中,M為煙花種群的數(shù)量。通過概率做出的選擇,適應度值更優(yōu)的煙花有更大的機會參與下一次迭代。
4.6 算法偽代碼
使用隨機最佳插入的煙花算法求解TSP問題的流程如算法2所示:
算法2基于改進RBI的煙花算法
輸入:V={v1,v2,…,vn}。//TSP所有節(jié)點的集合
輸出:p={v[1],v[2],…,v[n],v[1]}。//一條完整路徑
(1)初始化。
初始化最大迭代次數(shù)C,煙花種群數(shù)M,爆炸煙花數(shù)m,爆炸參數(shù)Amax、Amin、Smax、Smin,變異參數(shù)xmin和xmax,常量l和k,控制參數(shù)α和θ,迭代次數(shù)c←1,Explosive集置空,Abandoned集置空。
(2)初始煙花。
改進RBI生成M個不同的初始煙花,并將其加入煙花種群集合Fireworks中。
(3)開始迭代。
Whilec≤CDo
(4)選擇策略。
通過式(6)計算Fireworks中煙花的適應度值;
從Fireworks中選擇最優(yōu)煙花加入Explosive;
通過式(15)計算Fireworks集中剩余M-1個候選煙花的選擇概率;
輪盤賭選擇m-1個煙花加入Explosive集中;
(5)資源分配。
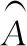
ForpinExplosiveDo
(6)爆炸算子。
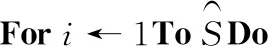
pin←p;
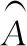
用改進RBI算法將刪除點重新插入pin中,得到新路徑pout;
通過式(6)計算pout的適應度值;
若fout>fin,則將pout加入Fireworks中;
若fout EndFor (7)變異算子。 統(tǒng)計煙花p產生的有效火花數(shù)s; pin←p; 通過式(14)計算x; 隨機刪除pin中的一段包含x個節(jié)點的路徑; 用改進RBI算法將刪除點重新插入pin中,得到新路徑pout; 將pout加入Fireworks中; 將煙花p從Fireworks集移至Abandoned集中; EndIf EndFor (8)更新變量。 c←c+1,Explosive集置空; 更新M為Fireworks集的煙花個數(shù); EndWhile (9)返回結果。 返回Fireworks和Abandoned中適應度最優(yōu)的解 (10)結束。 由于算法總迭代次數(shù)是C,每次迭代產生的火花數(shù)為S=m·k,每個火花平均探索n/l的城市規(guī)模,最多探索n的城市規(guī)模,因此算法的時間復雜度為O(kmnC)。 為檢測本文算法的性能,從TSPLIB數(shù)據(jù)集中選取了Oliver30、Eil51等6個數(shù)據(jù)集進行測試,并使用本文算法RBIFWA與基本煙花算法FWA[6]、混沌煙花算法CFWA[15]、離散蝙蝠算法DBA[4]、自適應模擬退火蟻群算法SA-MMAS[5]進行實驗對比。實驗環(huán)境為Python,CPU 3.2 GHz,內存8 GB,Windows 10 64位操作系統(tǒng)。本文算法RBIFWA的參數(shù)取值如下:總迭代次數(shù)C=1000,隨機因子r=10,初始煙花種群數(shù)M=10,爆炸煙花數(shù)m=5,爆炸半徑的最大值Amax=0.8n(n為城市的規(guī)模)和最小值Amin=3,爆炸火花數(shù)量的最大值Smax=0.8n和最小值Smin=3,允許變異的最大節(jié)點數(shù)xmax=0.6n和最小節(jié)點數(shù)xmin=8,常量l=2,平均爆炸火花數(shù)量k=5,控制參數(shù)α=0.25,θ=2。此時算法每次迭代都產生mk=25個左右的煙花種群數(shù)量。其余算法的參數(shù)設置均參考相應論文實驗,時間復雜度及主要參數(shù)設置如表1所示。 Table 1 Comparison of algorithm time complexity and main parameters 其中,C為最大的迭代次數(shù),M為每次迭代參與的種群數(shù)量,n為城市的規(guī)模。由于算法的時間復雜度相同,城市規(guī)模n大于25時,RBIFWA收斂到最優(yōu)解所用的迭代次數(shù)小于其他算法的,即可表明本文算法優(yōu)秀的求解能力。由于不同算法每次迭代的運算量不同,因此結合迭代次數(shù)及目標函數(shù)評估次數(shù)(FEs)進行比較,共計進行30次實驗,實驗結果如表2所示。 從表2可以看出,RBIFWA 的求解精度優(yōu)于其他算法的。針對這6個數(shù)據(jù)集,DBA的平均誤差為2.87%,SA-MMAS的為0.44%,F(xiàn)WA的為5.34%,CFWA的為0.51%,RBIFWA的為0.16%。從平均迭代次數(shù)和平均目標函數(shù)評估次數(shù)上來看,RBIFWA具有明顯的優(yōu)勢,可見RBIFWA用更少的目標函數(shù)評估次數(shù)和更少的種群數(shù)量,便可以得到相對更優(yōu)的結果。與FWA相比,改進的隨機最佳插入算法能夠構造精度更高的解,極大減少了搜索時的迭代次數(shù)和種群數(shù)量,使煙花算法擁有更強的收斂能力。與DBA和SA-MMAS相比,RBIFWA表現(xiàn)出更出色的求解能力,這主要是因為適應度更優(yōu)的煙花能夠產生更多的火花,使其能夠在鄰域中多次探索更優(yōu)解,優(yōu)秀的局部搜索能力使算法更快收斂,在減少迭代次數(shù)的同時,也提高了算法的精度。在選擇策略上,適應度更優(yōu)的煙花更有機會加入下一次爆炸,也進一步提高了算法局部搜索能力。因此整體來說,RBIFWA擁有更加優(yōu)秀的性能,能夠更快地收斂,且求得的最優(yōu)解更加精確。 Table 2 Results comparison of five algorithms 但是,當問題規(guī)模進一步擴大時,RBIFWA使用較小的種群數(shù)量極易陷入局部最優(yōu)解,為此適當增大種群數(shù)量可以增加種群多樣性,提高算法全局搜索能力。圖3對比了煙花種群數(shù)量分別設為L1:25(m=5,k=5),L2:50(m=5,k=10),L3:50(m=10,k=5)時求解TSPLIB數(shù)據(jù)集中城市規(guī)模為280的子集a280數(shù)據(jù)集的進化趨勢的結果,由于每次迭代的種群數(shù)量不同,因此實驗以最大目標函數(shù)評估次數(shù)為20 000次作為迭代終止的條件,并各進行了10次實驗,得到如圖3所示的不同種群數(shù)量的進化趨勢圖。其中圖3a和圖3c所示分別為最優(yōu)適應度值和種群多樣性的進化趨勢,圖3b和圖3d所示分別為圖3a和圖3c前700次的局部放大圖。 Figure 3 Evolutionary trends of different populations圖3 不同種群數(shù)量的進化趨勢圖 (1)圖3a中,煙花種群數(shù)量為L1時RBIFWA算法最終收斂至2 712.22,而煙花種群數(shù)量為L2和L3時RBIFWA算法分別收斂至2 689.45和2 651.47,可見隨著種群數(shù)量的增加,算法的尋優(yōu)能力也得到加強,使解的精度得到提升(圖3b和圖3c解釋了其原因)。 (2)圖3b中,煙花種群數(shù)量為L1時RBIFWA算法收斂都較煙花種群數(shù)量為L2和L3時快,但尋優(yōu)能力較弱,這說明當種群數(shù)量較小時,算法收斂速度較快,極易陷入局部最優(yōu)解。 (3)圖3c中,煙花種群數(shù)量為L2和L3時RBIFWA算法種群多樣性較煙花種群數(shù)量為L1時有很大的提升,這說明隨著種群數(shù)量的增加,更容易探索到新解,結合圖3a可見,種群多樣性的提升使算法更容易跳出局部最優(yōu)解,因此有更強的全局搜索能力。 (4)對比種群數(shù)量相同的L2和L3發(fā)現(xiàn),煙花種群數(shù)量為L3時算法較煙花種群數(shù)量為L2時有更高的種群多樣性,但煙花種群數(shù)量為L2比煙花種群數(shù)量為L3時的收斂速度更快,這主要是因為隨著m的增大,更多的煙花參與探索,提高了煙花爆炸產生有效火花的能力,即決定了全局搜索能力;而平均爆炸數(shù)量k的增加,使煙花能夠在鄰域中進行多次探索,更有機會得到更優(yōu)解,即決定了局部搜索能力。圖3d中,煙花種群數(shù)量為L3時與煙花種群數(shù)量為L1時算法結果差距明顯,而煙花種群數(shù)量為L2時的多樣性與煙花種群數(shù)量為L1時相當,也進一步說明了m對全局搜索能力的作用。 因此,對于問題規(guī)模較大的測試算例,適當增加煙花種群的數(shù)量,可以提升解的精度。另外,當種群數(shù)量相同時,增大m減小k可以提高算法全局搜索能力;增大k減小m可以提高算法局部搜索能力。 本文考慮了TSP離散的特征以及煙花算法的尋優(yōu)機制,設計了一種隨機最佳插入煙花算法。該算法在減少迭代次數(shù)的同時也提高了求解精度。這是由于算法改進了爆炸資源的分配方式和煙花選擇的策略,使適應度更優(yōu)的煙花能夠在爆炸過程中產生更多的火花去探索鄰域最優(yōu)解,從而有效提升算法的收斂速度。通過對比實驗發(fā)現(xiàn),本文算法無論在時間性能上還是求解精度上都有著優(yōu)秀的表現(xiàn)。為了進一步改進以及拓展算法,未來將探索引入并行操作,并結合鄰域搜索等算法,進一步提高算法性能和求解精度,以期解決更大規(guī)模的TSP問題。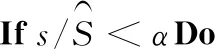
5 實驗仿真與結果分析


6 結束語

