變壓器在線監測數據異常值檢測與清洗

2020-11-30 08:32:32錢宇騁甄超季坤趙常威付龍明張亞靜

哈爾濱理工大學學報 2020年5期

錢宇騁甄超季坤趙常威付龍明張亞靜

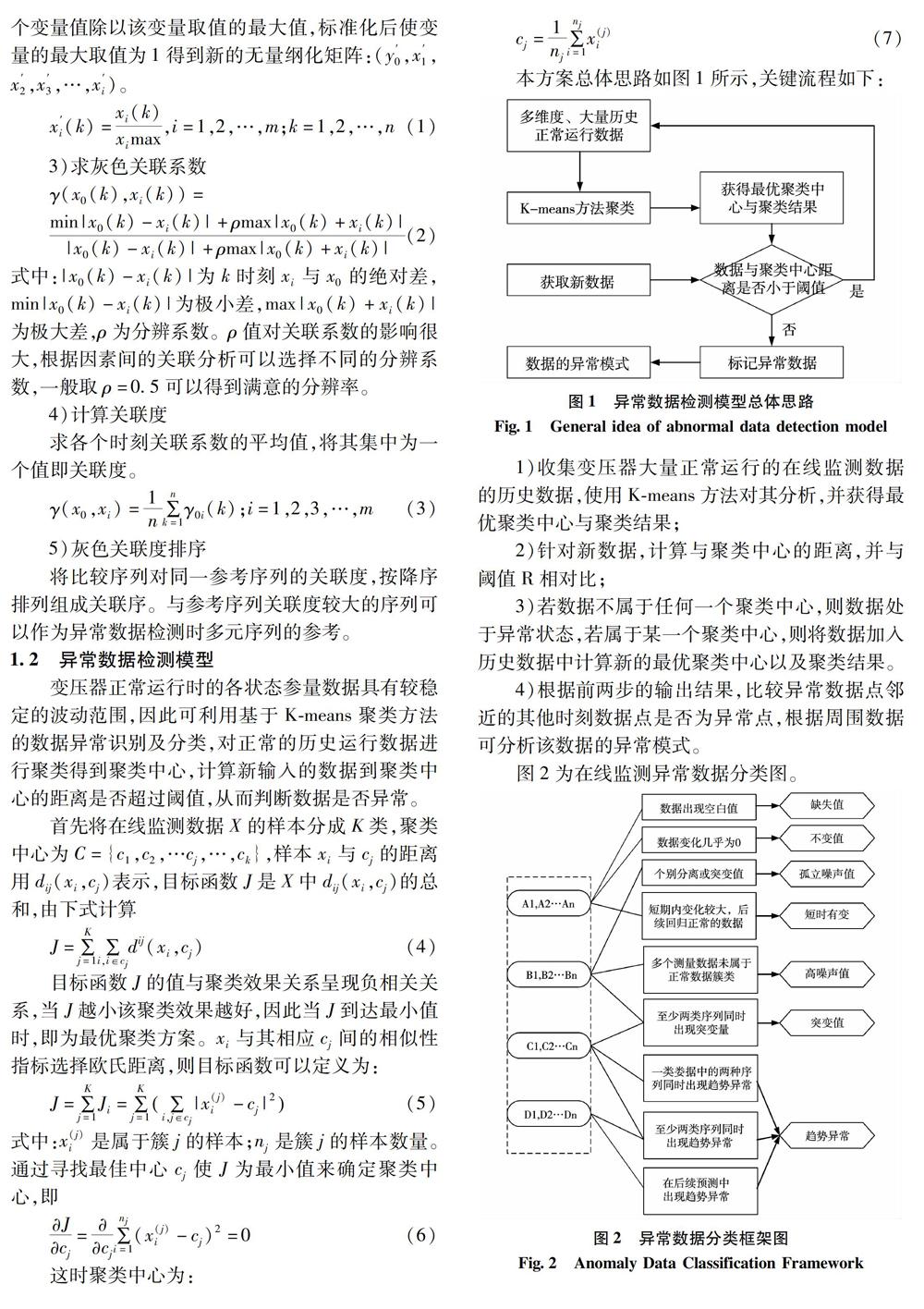
摘要：在線監測數據能夠實時監測變壓器狀態，然而經調查發現存在數據不可靠的問題，直接關系到后續狀態評估的準確性。針對在線監測數據中異常值特點，以及一般的異常狀態檢測方法是基于閾值，噪聲數據難以及時甄別的問題，提出了一種基于灰色關聯度和K-means聚類的方法。利用灰色關聯法對在線監測的多元時間序列數據進行關聯度挖掘，提取出關聯性強的序列為后續多元序列異常數據檢測提供依據;其次建立基于k-means聚類的方法建立數據的異常檢測模型;最后研究了時間序列預測方法，完成趨勢預測并填充缺失值和噪聲值，保持數據完整性。通過某變電站的在線監測數據對此算法進行驗證，結果表明該方法可及時完成異常檢測及清洗，清洗后準確率93.9%，完備率可達98.6%，有較高使用價值。

關鍵詞：變壓器;在線監測數據;K-means聚類;異常值檢測;時間序列

DOI：10.15938/j.jhust.2020.05.003

中圖分類號： TM411

文獻標志碼： A

文章編號： 1007-2683（2020）05-0015-08

Abstract：The online monitoring data can monitor the status of the transformer in real time. However， it is found that there is a problem of unreliable data， which is directly related to the accuracy of the subsequent status assessment. In view of the characteristics of abnormal values in online monitoring data， and the general abnormal state detection method is based on the threshold， it is difficult to distinguish the noise data in time， so a method based on gray correlation and K-means clustering is proposed. The gray correlation method is used to mine the degree of association of online multivariate time series data， and the strong correlation sequence is extracted to provide a basis for the subsequent multivariate sequence anomaly data detection. Secondly， an anomaly detection model based on k-means clustering method is established. Finally， the time series forecasting method is studied， the trend forecast is completed and the missing values and noise values are filled to maintain data integrity. The algorithm is verified by the online monitoring data of a substation. The results show that the method can complete abnormal detection and cleaning in time. The accuracy rate after cleaning is 93.9%， and the completion rate can reach 98.6%， which has high use value.

Keywords：transformer; online monitoring data; K-means clustering; outlier detection; time series

0 引言

近年來，電力系統是否能安全穩定運行等問題引起用戶廣泛關注，電力公司不斷推進智能電網建設，逐步擴大變壓器實時監測的廣度與深度，利用傳感器裝置不間斷地測量反映設備運行狀態的關鍵特征參量。針對變壓器的狀態監測手段在國內外已有較多的研究，主要包括變壓器的繞組溫度[1]、頂層油溫、局部放電、油中氣體含量分析（dissolved gas analysis，DGA）[2]等。然而數據的質量不高會影響狀態評估時準確率，因此診斷分析之前，進行異常數據檢測與清洗十分必要。

現階段針對變壓器的油中溶解氣體分析、基于頻率響應的繞組狀態監測[3]以及基于油中糠醛、紙聚合度[4]等單一系統的設備信息異常數據的檢測，通過設定閾值[5]進行分析，方法簡單但準確率不高。

聚類方法作為大數據中的一項成熟技術[6]，通過將聚類方法與神經網絡[7]、滑動窗口[8]、層次分析法[9]、支持向量機等方法結合，實現參數優化或樣本轉換，有許多用于變壓器檢測的程序。但是，分離的噪聲數據會被直接刪除，這會破壞狀態數據的連續性。上述研究導致數據清理過程中的數據丟失，這不利于后續狀態評估。近年來，國內外研究人員也將時間序列模型（auto regressive moving average，ARMA）引入電力應用[10]，主要應用于電路故障診斷及階段故障率預測[11]、發電量預測[12]、電力負荷預測[13]，通過ARMA時間序列分析模型將去除的噪聲數據補足以提高狀態評估時的準確性。總的來說，應用在負荷預測中較多，但在狀態監測方面很少，由于時間序列能夠表征狀態監測的數據流，將成為狀態監測中大數據技術的一個發展趨勢。

基于以上分析，提出一種基于K-means和時間序列分析的變壓器異常值檢測與清洗的方法。通過灰色關聯法從多維的在線監測數據流中篩選關聯度高的相關序列，然后基于K-means方法對在線監測數據進行異常檢測，利用時間序列預測方法完成噪聲數據清洗及趨勢預測。本文方法可完成在線監測數據異常檢測，完成修正噪聲點填補缺失值的清洗工作，祛除外界噪聲值或突變值的影響，并且對后期時間序列數據預測分析，及時發現趨勢異常。

1 異常數據檢測模型的建立

變壓器在線監測狀態信息數據，通過傳感器采集、傳輸后集成在數據信息平臺上。按時間先后順序排列的特征量數據，可認為采集的在線數據形成了一個連續而完整的時間序列。但由于傳感器短時失效、通訊端口異常、裝置老化以及一些人工失誤等多種因素的存在，收集的狀態信息數據會不可避免出現多種狀態的異常值[14]。在線監測異常數據的產生有多種原因，噪聲值，這部分數據是與變壓器自身無關，數據測量或傳輸系統受到外部環境因素的干擾而意外失靈包括缺失值、不變數據值、孤立噪聲值、短時有變數據值。由裝置異常引起的異常數據，持續性缺失值，高噪聲或高方差異常數據，關聯性性強的狀態量同時出現突變，關聯性強的檢測量上升趨勢異常。因此，提出基于灰色關聯分析與K-means聚類方法對在線監測數據異常檢測。

1.1 多元時間序列關聯挖掘

在線監測數據類型繁多，實現特征提取顯得十分必要，本節將對在線監測數據的多元時間序列進行關聯度挖掘，提取出關聯性強的序列為后續多元序列異常數據監測提供依據。實時狀態信息中提取關鍵參量不僅能縮減處理時間，降低在線監測數據的復雜性，更能有力保證狀態數據處理高效性、有效性，為電網運行實時提供檢修、調度決策。

在線監測參量大都是隨時間發生連續變化的數據[15]，灰色關聯分析非常適合于歷史動態分析，可以提供發展和變化情況的定量度量，因此使用灰色關聯方法來度量相關序列。該分析法衡量關聯程度是根據變量間發展趨勢的相似程度，若兩條曲線同步波動變化相似，則關聯度較高，反之較低[16]。下面給出灰色關聯分析模型計算的5個步驟。

1）確定分析的序列矩陣

2）對變量序列進行無量綱化

由于在線監測數據屬性差異不同，導致度量標準也亦不同，會對最后的結論造成一定的影響。因此根據式（1）無量綱化，采用極值化的方法，即每一個變量值除以該變量取值的最大值，標準化后使變量的最大取值為1得到新的無量綱化矩陣：（y′0，x′1，x′2，x′3，…，x′i）。

3）求灰色關聯系數

4）計算關聯度

求各個時刻關聯系數的平均值，將其集中為一個值即關聯度。

5）灰色關聯度排序

將比較序列對同一參考序列的關聯度，按降序排列組成關聯序。與參考序列關聯度較大的序列可以作為異常數據檢測時多元序列的參考。

1.2 異常數據檢測模型

變壓器正常運行時的各狀態參量數據具有較穩定的波動范圍，因此可利用基于K-means聚類方法的數據異常識別及分類，對正常的歷史運行數據進行聚類得到聚類中心，計算新輸入的數據到聚類中心的距離是否超過閾值，從而判斷數據是否異常。

首先將在線監測數據X的樣本分成K類，聚類中心為C={c1，c2，…cj，…，ck}，樣本xi與cj的距離用dij（xi，cj）表示，目標函數J是X中dij（xi，cj）的總和，由下式計算目標函數J的值與聚類效果關系呈現負相關關系，當J越小該聚類效果越好，因此當J到達最小值時，即為最優聚類方案。xi與其相應cj間的相似性指標選擇歐氏距離，則目標函數可以定義為：

1）收集變壓器大量正常運行的在線監測數據的歷史數據，使用K-means方法對其分析，并獲得最優聚類中心與聚類結果;

2）針對新數據，計算與聚類中心的距離，并與閾值R相對比;

3）若數據不屬于任何一個聚類中心，則數據處于異常狀態，若屬于某一個聚類中心，則將數據加入歷史數據中計算新的最優聚類中心以及聚類結果。

4）根據前兩步的輸出結果，比較異常數據點鄰近的其他時刻數據點是否為異常點，根據周圍數據可分析該數據的異常模式。

2 基于ARMA模型的在線數據預測模型建立

上一節對變壓器在線監測狀態量，利用聚類及關聯分析分析出異常數據，并劃分了不同類型，本節利用時間序列ARMA分析模型清洗異常數據，并預測后續發展及時發現趨勢異常。

2.1 在線監測數據時間序列表征

通過各個傳感器完成變壓器在線狀態量的監測結果，按時間先后順序排列的特征量數據[15]，可認為采集的在線數據形成了一個連續而完整的時間序列。由影響因素發生作用的大小和方向變化不同可分為三類。

平穩時間序列：隨著時間的變化，狀態變量并不隨之變化。波動幅度隨時間變化：隨著時間變化，狀態變量的方差發生變化。非平穩時間序列：有兩種，趨勢性時間序列，表現為監測變量隨著時間的變化呈現出變動趨向，持續性、長期性出現較緩慢的上下。周期性時間序列，表現為監測變量隨著季節或者其他周期的交替出現高峰與低谷，周期內的時間序列有相似的特征。由此選取變壓器在線監測的實時數據以下幾類，作為后續在線數據預測算法的基礎。然而閃絡放電的電壓、電流等突變的數據類型，屬于有用的故障信息不能舍去，所以在此不能適用于時間序列分析方法。

1）短期平穩長期緩慢上升序列：該類數據包括微水、氫氣、CH4、C2H4、C2H6等。

2）長期平穩序列：無明顯下降趨勢，僅在設備狀態異常時數值會明顯升高。該類數據包括鐵芯接地電流、C2H2、套管全電流等。

3）短至長期均為緩慢上升序列：監測數據中的CO和CO2數據長期表現為向上的趨勢。這類數據可通過差分運算進行變換，對非平穩序列的均值平穩化預處理，通過這種方法可以將趨勢性去除，變為平穩性序列。

4）周期性序列，通常以天為單位：包括變壓器繞組、頂層、底層等的油溫，在實際清洗過程中先用季節差分將這些數據變為平穩時間序列，再進行擬合，以降低計算的復雜度。

2.2 基于時間序列異常數據預測模型

對變壓器未來的異常狀況進行預測，需要對變壓器未來的在線監測數據的情況進行分析。時間序列的趨勢會持續到最近的未來，因此通過自回歸滑動平均模型ARMA來分析研究時間序列[17]，對于一個時間序列{x1，x2，…，xn，…}表達式如下。

3 算例分析

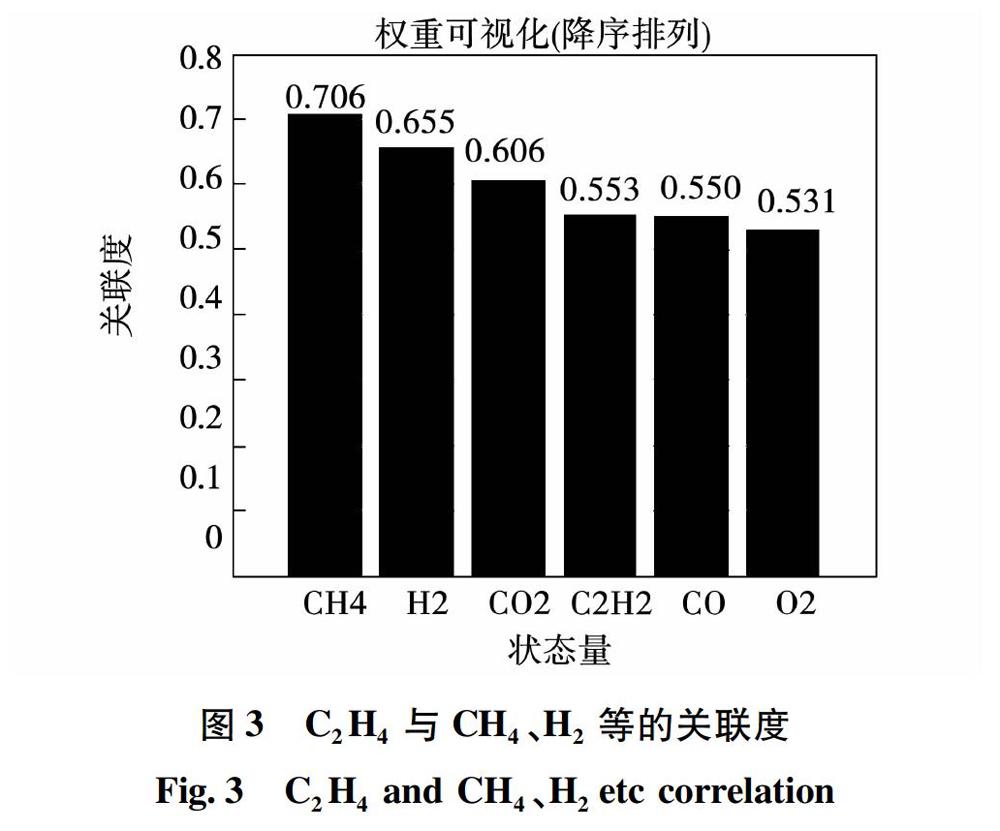
選取某變電站1號變壓器為例，對繁多的在線監測數據類型實現特征提取，按照1.1節中灰色關聯分析法的計算步驟，對多元時間序列進行關聯度挖掘。以將C2H4作為參考序列，CH4、H2、C2H2、CO、CO2、O2作為比較序列為例，建立分析矩陣，對矩陣中的各個序列按式（1）進行無量綱化，得到新的矩陣，計算關聯系數后由式（3）即可得到關聯度如圖3所示。可知C2H4和H2及CH4三種參量關聯較高，聚類分析時綜合考慮這三種氣體。

應用改進的K-means算法進行變壓器異常狀態快速識別。對此變壓器2016年1月2日-2016年8月25日間，以CH4為例將其327組變壓器正常歷史數據樣本輸入到聚類算法中，按照正常數據類型的性質取k=3。如圖4所示，聚類結果輸出3個聚類簇，三個聚類簇中數據與中心距離的最大值分別是209.3751、272.0998與232.7127。

將3個聚類簇中數據與中心距離的最大值乘上常數D作為R。選取該變電站同型號設備100組待檢測數據，判斷數據是否異常，D取不同值時檢測結果有不同準確率，當D取1時檢測效果較好。但是D的取值范圍并非一成不變，在實際運行中需要根據具體數據或經驗進行調整，可選取待測數據進行調試，選取準確率最高時的D值。

將選取的待檢測數據根據1.2節K-means聚類分析模型，通過判斷數據集里每個時間點的數據與聚類中心間的距離與閾值的大小，來判斷是否屬于正常簇，結果如圖5所示（1表示異常數據，0表示正常數據），關聯度分析可知C2H4和H2及CH4的關聯較高，所以將這三種氣體綜合考慮。

以異常數據判斷結果圖中的CH4聚類結果為例可以看出，主要存在以下種類型的數據：

1）在T=50、T=201等時間點，均不屬于3個聚類簇，但是其周圍時刻的數據均正常，則此時是噪聲點，可能是由于某傳感器不穩定造成，可以將此忽略，去除此時的孤立噪聲值，并通過進一步的時間序列分析方法，對去除噪聲值的部分填充，以免去除值后的空白對后續的變壓器狀態評估造成影響。

2）在T=100～110，出現連續數據為異常數據點，推斷可能是傳輸設備在該段時間出現了不穩定的運行狀態或者受到了干擾，經查驗采集設備并未發生狀態異常，可能是因為數據錄入導致的數據空白，此時需要通過進一步的時間序列分析方法，對空白數據填充，以免空缺值對后續的變壓器狀態評估造成影響。

3）在T=240之后，大段連續數據均出現異常，由此推斷設備在該時刻后出現了可能的異常狀態。此時參考C2H4和H2兩種氣體的聚類結果，兩類氣體大概在T=255左右均出現連續數據異常，由此可以推斷出大概率變壓器出現了病變，應該發出告警，并需要盡快安排設備健康狀態評估以及相應的檢修手段。

對時間T=50、T=201去除了噪聲值，T=100～110時為數據缺失值，出現數據丟失的情況，通過ARMA時間序列分析模型擬合在線監測數據，將其補足以提高評估準確性，以CH4為例說明方法的有效性。根據自相關系數和偏自相關系數確定 ARMA（p，q）模型階數，繪制序列的自相關函數和偏相關函數分別如圖 6和圖 7所示。

4 結語

1）本文針對在線監測數據中異常值特點，提出基于灰色關聯度和K-means聚類算法對變壓器在線監測數據異常檢測。可表征關聯度高的相關序列，并快速及時完成在線監測數據異常檢測并分類，并利用時間序列預測方法完成噪聲清洗，祛除外界噪聲值或突變值的影響，提高告警準確率，解決了傳統閾值判定方法誤判情況。但存在一定局限性，如聚類算法對如何選取參數、聚類個數k均沒有合適的方法，需要基于訓練數據進行參數優化。

2）利用時間序列預測方法針對異常數據中的噪聲點，進一步進行補充優化，為后續預測數據趨勢打下基礎，解決了因數據噪聲點引起的數據預測失誤問題，提高后續狀態診斷的準確率。

3）改進之處在于本文提出的方法目前僅針對變壓器的在線監測數據實行了現實應用，并能達到較高效用，但是對于其他的電力設備如輸電線路、GIS等設備在線監測數據的異常檢測需進一步驗證。

參考文獻：

[1] 張喜樂，何松坡，王建民，等.換流變壓器繞組損耗及熱點溫升的仿真研究[J].變壓器，2019，56（7）：24.

ZHANG Xile，HE Songpo，WANG Jianmin，et al. Numerical Simulation of Winding Loss and Hot Spot Temperature Rise for Converter Transformer[J]. Transformer，2019，56（7）：24.

[2] 李文志，朱娟.變壓器油色譜數據異常的原因分析及處理[J].電工技術，2020（1）：115.

LI Wenzhi，ZHU Juan. Cause Analysis and Treatment of Abnormal Oil Chromatographic Data of Transformer[J]. Electric Engineering，2020（1）：115.

[3] 陳一鳴，梁軍，張靜偉，等.基于改進參數辨識的三繞組變壓器繞組狀態在線監測方法[J].高電壓技術，2019，45（5）：1567.

CHEN Yiming，LIANG Jun，ZHANG Jingwei，et al. Method of Online Status Monitoring for Windings of Three-winding Transformer Based on Improved Parameter Identification[J]. High Voltage Engineering，2019，45（5）：1567.

[4] 李元，張崟，唐峰，等.利用近紅外光譜定量評估絕緣紙聚合度的建模方法研究[J].中國電機工程學報，2019，39（S1）：287.

LI Yuan，ZHANG Yin，TANG Feng，et al. Investigations on Quantitative Evaluation Modeling for Determining the Degree of Polymerization of Insulating Paper by Near Infrared Spectroscopy[J]. Proceedings of the CSEE，2019，39（S1）：287.

[5] 中華人民共和國國家經濟貿易委員會.變壓器油中溶解氣體分析和判斷導則：DL/T722—2000[S].北京：中國電力出版社，2001.

[6] 王亞萍，李士松，葛江華，等.等距離映射和模糊C均值的滾動軸承故障識別[J].哈爾濱理工大學學報，2019，24（3）：41.

WANG Yaping，LI Shisong GE，Jianghua，et al. Rolling Bearing with Isometric Feature Mapping and Fuzzy C-means Fault Identification Method[J]. Journal of Harbin University of Science and Technology，2019，24（3）：41.

[7] 徐京京. 基于聚類和神經網絡的異常數據識別算法研究[D].北京：華北電力大學，2019.

[8] 嚴英杰，盛戈皞，劉亞東，等.基于滑動窗口和聚類算法的變壓器狀態異常檢測[J].高電壓技術，2016，42（12）：4020.

YAN Yingjie，SHENG Gehao，LIU Yadong，et al.Anomalous State Detection of Power Transformer Based on Algorithm Sliding Windows and Clustering[J]. High Voltage Engineering，2016，42（12）：4020.

[9] 王楠，王偉，張鑫，等.改進的層次分析法在變壓器油紙絕緣狀態評估中的應用[J].高壓電器，2019，55（12）：187.

WANG Nan，WANG Wei，ZHANG Xin，et al. Application of Improved Analytic Hierarchy Process in Transformer Oil-paper Insulation State Evaluation[J]. High Voltage Apparatus，2019，55（12）：187.

[10]李波，林聰，劉清蟬，等.基于時序建模的光纖電流互感器隨機噪聲卡爾曼濾波方法[J].電機與控制學報，2017，21（4）：83.

LI Bo，LIN Cong，LIU Qingchan，et al. Kalman Filter Offiber Optical Current Transducer's Stochastic Noise Based on Time Series Model[J]. Electric Machines and Control，2017，21（4）：83.

[11]邊寧，許允之.基于ARMA和遺傳算法優化的BP神經網絡電動機斷條故障診斷[J].煤礦機電，2017（3）：23.

BIAN Ning，XU Yunzhi. Fault Diagnosis of BP Neural Network Based on ARMA and Genetic Algorithm Optimization[J]. Colliery Mechanical & Electrical Technology，2017（3）：23.

[12]范金驥.基于ARMA與ANN模型組合交叉方法的電網日負荷預測[J].浙江電力，2018，37（8）：35.

FAN Jinji. Daily Grid Load Forecasting Based on ARMA and ANN Model Combined Crossing Method[J]. Zhejiang Electric Power，2018，37（8）：35.

[13]徐桐陽.ARMA模型對山西省火電在全國比重的擬合應用[J].中國市場，2015（34）：93.

XU Tongyang. The Fitting Application of ARMA Model to the Proportion of Thermal Power in Shanxi Province in the Country [J]. Chinese Market， 201534）： 93.

[14]何堯，梁宏池，連鴻松，等.基于滑動窗口和多元高斯分布的變壓器油色譜異常值檢測[J].高壓電器，2020，56（1）：203.

HE Yao，LIANG Hongchi，LIAN Hongsong，et al. Outlier Detection of Power Transformer Oil Chromatographic Data Based on Algorithm Sliding Windows and Multivariate Gaussian Distribution[J]. High Voltage Apparatus， 2020， 561）： 203.

[15]FAN Jingmin，FU Chenyang，YIN Hao，et al. Power Transformer Condition Assessment Based on Online Monitor with SOFC Chromatographic Detector[J]. International Journal of Electrical Power and Energy Systems，2020，118：105805.

[16]PRAKASH K Soorya，GOPAL PM，KARTHIK S. Multi-objective Optimization Using Taguchi Based Grey Relational Analysis in Turning of Rock Dust Reinforced Aluminum MMC[J]. Measurement，2020，157：107664.

[17]DING Feng，WAN Lijuan，GUO Yunze，et al. The Filtering-Based Auxiliary Model Generalized Extended Stochastic Gradient Identification for a Multivariate Output-error System with Autoregressive Moving Average Noise Using the Multi-innovation Theory[J]. Journal of the Franklin Institute，2020，357（9）：5591.

[18]CHRISTIAN H，WEI B. Regime-Switching Discrete ARMA Models for Categorical Time Series[J]. Entropy，2020，22（4）：458.

[19]KIM J Y， SOHN I， LEE K. Bayesian Cumulative Logit Random Effects Models With Arma Random Effects Covariance Matrix[J]. Journal of the Korean Statitical Society， 2020， 49（1）：32.

[20]汪磊，楊星月，高杉.基于時間序列模型的民航擦機尾事件預測研究[J].安全與環境工程，2020，27（2）：216.

WANG Lei，YANG Xingyue ，GAO Shan. Prediction of the Incidence of Tail Striking Based on Time Series Model[J]. Safety and Environmental Engineering， 2020，272）： 216.

（編輯：溫澤宇）