基于BP神經網絡技術的電離層VTEC融合

郭承軍，龐國強

電子科技大學 電子科學技術研究院，成都 611731

電離層是指60 km至幾千千米的區域，電離層會隨著季節和經緯度的變化而發生變化[1]。隨著季節的變化，太陽和地球的相對位置不斷變化，太陽對電離層的輻射強度不同，導致電子含量變化，一般夏季電離層高，電子含量大，而冬季電離層低，電子含量小[2]。在衛星導航系統中，電離層會對導航信號在空間的傳輸過程產生影響[3]。電離層也會對人們的生產生活產生影響，因此研究電離層的物理特性變得很重要，提高電離層反演精度的要求越來越高，獲得高精度的全球電離層地圖也變得尤為重要。全球電離層地圖由世界范圍內幾百個地面基站測繪而成[4]，按照緯度間隔2.5°、經度間隔5°，將全球劃分為5 183個格網點，利用全球范圍內的監測站計算出全球電離層總電子含量(total electron content，TEC)分布圖[5]。隨著電離層探測技術的發展，電離層觀測資料增多，使用單一的電離層觀測數據獲得電離層精度不能滿足人們的要求，針對這一問題，通過數據融合技術將多種來源的觀測資料融合在一起提高電離層的反演精度。

為了更好地探測電離層，許多學者進行了電離層數據融合技術方面的研究。Fisher等將數據融合技術與多層前饋神經網絡相結合，以改善斜入射電離圖的反演，與直接融合電離圖陣列數據相比，在融合之前使用分層網絡對電離圖進行反轉，會獲得更好的結果[6]。Hu等提出一種融合模型使用人工神經網絡技術補償二維多項式電離層延遲校正模型的偏差，并將其與二維多項式電離層延遲校正模型進行比較，所提出的模型比二維多項式電離層延遲校正模型具有更好的精度[7]。Zheng等通過BP神經網絡技術開發了用于補償IRI2012偏差的融合模型，BP神經網絡和IRI2012模型的預測值分別與觀察到的數據進行比較，提出的模型優于IRI2012模型[8]。Yazdan等提出了一種基于IRI 2007和伊朗永久GPS網全球定位系統觀測數據的新型區域VTEC模型。該模型由IRI模型的給定參考部分和未知修正項組成，更適用于在區域電離層模擬中比球諧函數更適用[9]。Mallika等提出一種基于主成分分析和人工神經網絡融合的電離層預測算法，以預測電離層總電子含量值，利用網格點的太陽指數、地磁指數和20年TEC數據來應用人工智能方法，實驗結果強調了該算法在預測電離層時延效應方面的可靠性[10]。

本文提出使用基于BP神經網絡進行地基觀測數據和IRI數據融合來獲得高精度的電子含量，將該方法應用到無觀測資料或者觀測資料較少的區域以獲得滿足要求的電離層電子含量精度。

1 電離層反演

電離層經驗模型主要有IRI模型、Bent 模型、Klobuchar模型等。IRI模型是由國際空間研究委員會(International Union of Radio Science，URSI)和空間研究委員會(Committee on Space Research，COSPAR)合作建立的，使用的是電離層實測數據[11-13]。由于IRI模型更精確，本文選擇IRI模型作為背景模型。

電離層分布在地表上空，電子含量與高度相關，為了將電離層模型化，電離層假設為距離地面一定高度的薄層，此為電離層單層模型，整個電離層的帶電粒子都集中分布在這個薄層上，薄層電子密度最大。因此，衛星發射信號與地面觀測站接收信號時要穿過該球殼，衛星與觀測站連線與該薄層的交點稱為穿刺點(ionospheric pierce point，IPP)，如圖1所示。通常設定電離層最大電子密度所在的高度為400 km，能更準確地描述電離層特征。圖1為電離層地基反演示意。

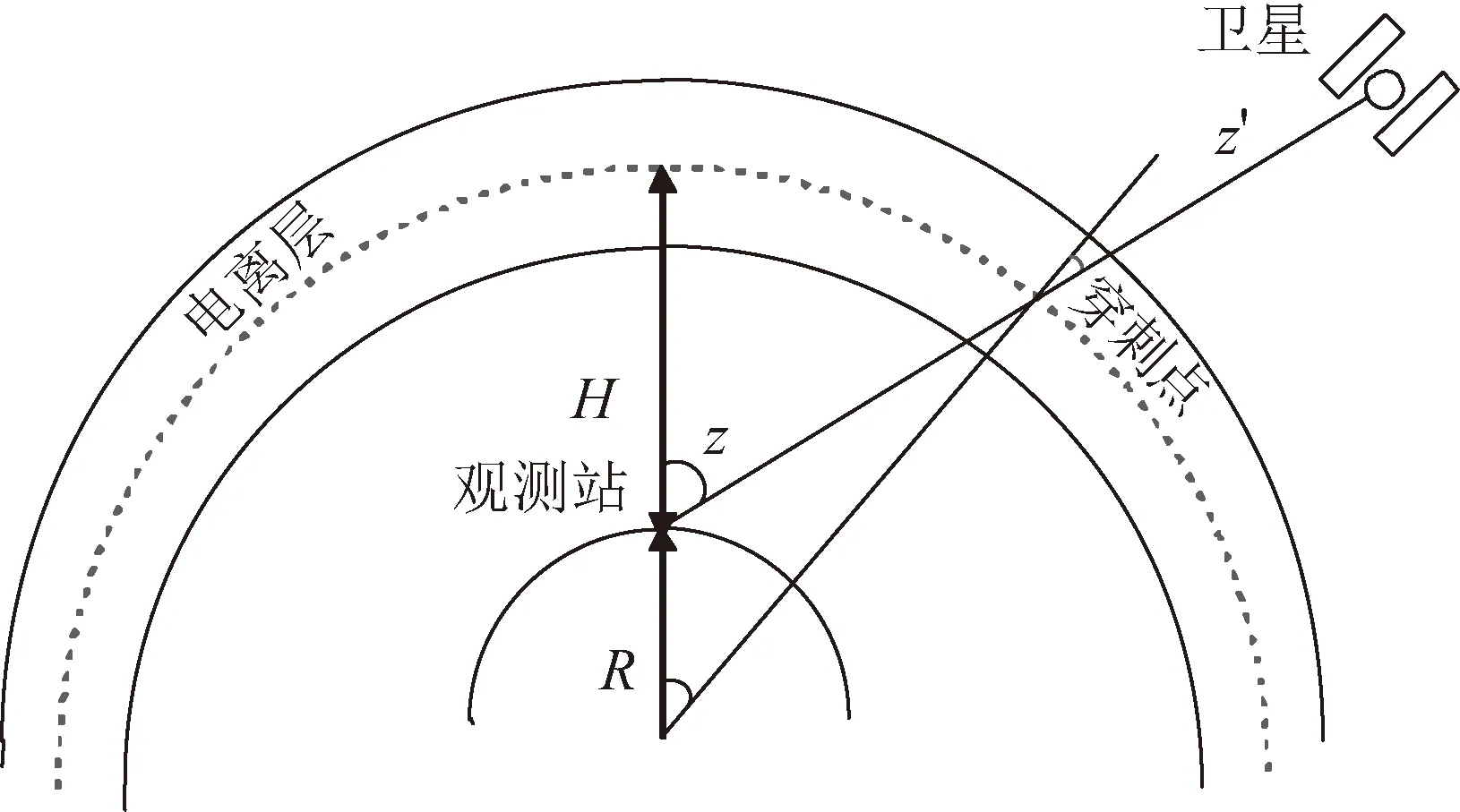
圖1 地基反演示意Fig.1 Ground-based inversion diagram

對同一電離層而言，衛星信號在電離層中的傳播路徑隨著觀測站至衛星天頂距z的增大而增大，而且傾斜總電子含量(slant total electron content， STEC)值也隨之增大。在觀測站位置天頂垂直方向上(z=0)的電子含量為電離層VTEC，在單層電離層模型中，VTEC與STEC可以建立如下關系式：

STEC=MF(z)·VTEC

(1)

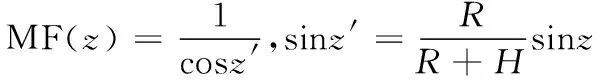
(2)

式中：H為電離層的高度；R為地球的半徑；z為觀測站信號路徑天頂距；z′為電離層穿刺點處的信號路徑天頂距；MF(z)為投影函數。

地基觀測值中包含偽距觀測值和載波觀測值。偽距測量雖然精度較低，但是可靠性高；載波相位測量精度高，但是需解算整周模糊度，計算過程復雜。所以，本文綜合利用載波相位測量精度高和偽距測量可靠性高的優點，采用載波相位平滑偽距的方式來提高觀測精度。

電離層TEC根據偽距觀測方程和載波相位觀測方程獲得，如下式所示：

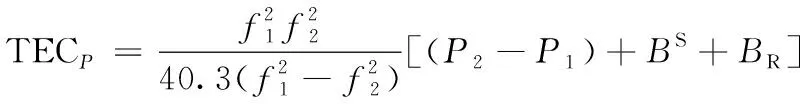
(3)

(λ1N1-λ2N2)-bS-bR]

(4)

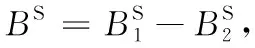
同一個觀測歷元n時，ΔTECn由TECP,n與TECΦ,n獲得：

ΔTECn=TECP,n-TECΦ,n

(5)

由遞歸算法獲得第N個歷元的ΔTECN的表達式如下：

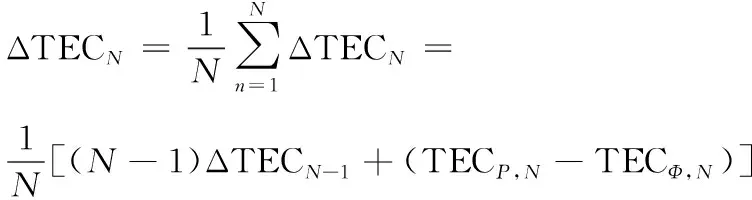
(6)

第N個歷元的TECN由式(7)計算獲得：

TECN=TECΦ,N+ΔTECN=

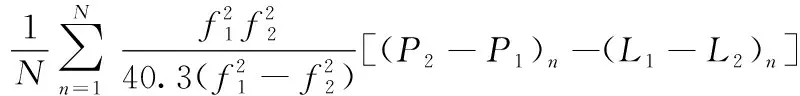
(7)

電離層單層模型是將電離層假設為一個薄球殼，雖然計算方便，但是仍然受觀測站數量以及分布情況的制約，地基電離層反演精度不是很理想[14]。因此，將地基觀測數據與IRI數據通過BP神經網絡方法獲得更高的電離層反演精度變得很重要。

2 基于BP神經網絡技術的電離層 VTEC融合

2.1 BP神經網絡

本文基于BP神經網絡的信號前向傳遞、誤差反向傳播的特點，根據預測誤差調整BP神經網絡的權值，從而更加接近期望輸出[15]。BP神經網絡的結構如圖2所示。

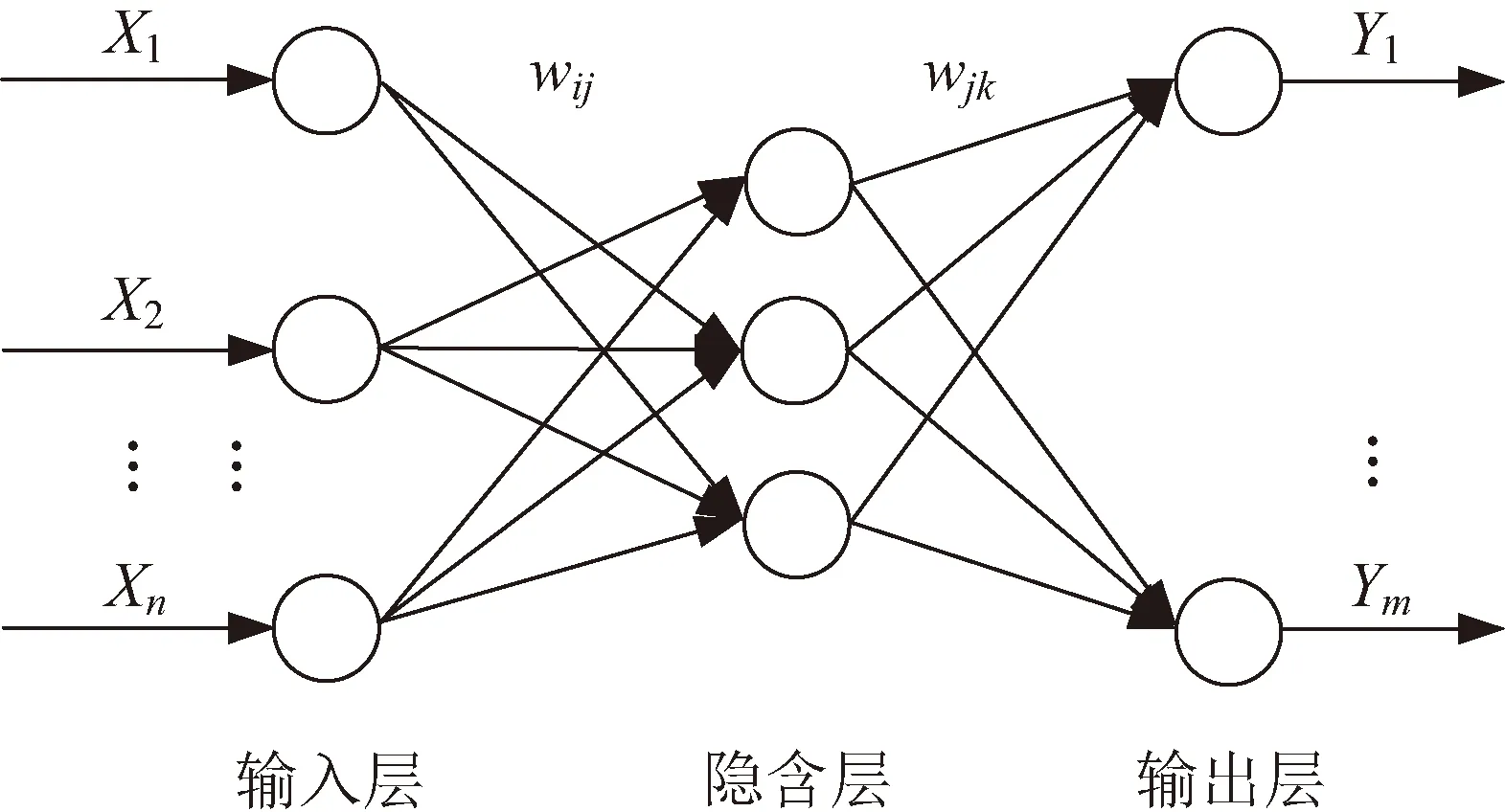
圖2 BP神經網絡結構圖Fig.2 BP neural network structure diagram

圖2中,X1，X2，…,Xn是輸入值，Y1,Y2,…,Ym是輸出值,wij和wjk為權值。本文選擇BP神經網絡將IRI模型和地基反演獲得的VTEC進行數據融合來獲得ΔTEC。

2.2 克里金插值法

克里金插值法是一種對變量的取值進行最優和無偏估計的方法[16-18]。

權值確定后采用式(8)計算待求點電子含量差值，即：

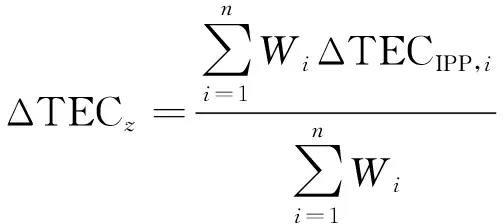
(8)

式中：ΔTECIPP,i為穿刺點電離層電子含量差值；Wi為電子含量數據的變異函數的倒數。

2.3 電離層VTEC融合方法

電離層數據融合方法就是將各種電離層觀測資料和電離層背景模型進行電離層觀測數據融合[19]。本文提出將IRI電離層模型作為背景模型，利用BP神經網絡及克里金插值法將地基觀測數據融合到IRI電離層模型來提高電離層的反演精度。該方法先利用BP神經網絡將IRI模型和地基反演獲得VTEC進行數據融合來獲得ΔVTEC，再通過克里金插值法獲得待求處的ΔTEC，并以待求處IRI為背景模型獲得待求處的VTEC。電離層VTEC融合流程如圖3所示。

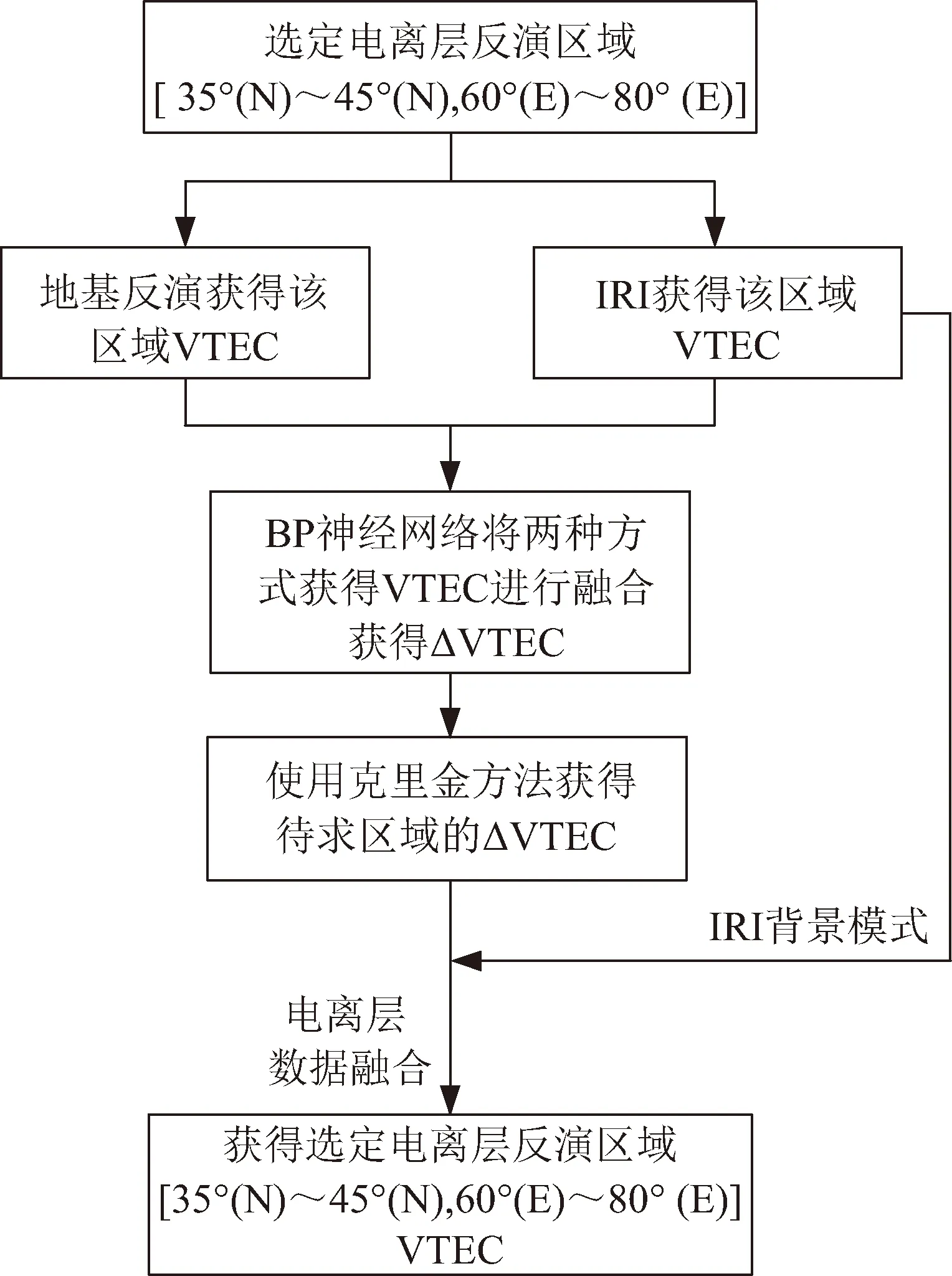
圖3 電離層VTEC融合流程Fig.3 Ionospheric VTEC fusion flowchart

3 試驗結果與分析

溫帶地區四季分明，所以使用溫帶地區[35°(N)～45°(N)，60°(E)～80°(E)]反演，選擇四季代表月1月、4月、7月、10月中的某一天(即2016年1月11日、4月11日、7月11日、10月11日)10時進行電離層反演試驗，將BP神經網絡數據融合和地基反演兩種方法獲得的VTEC與國際GNSS服務機構(International Globa1 Navigation Sate1lite System Service，IGS)的VTEC進行比較，以VTEC值小者除以大者獲得相對比值，相對比值范圍為0～1。用這兩種方式獲得的電離層反演試驗結果如圖4～圖7所示，反演效果評價標準如表1所示。反演試驗選擇該溫帶區域的3個觀測站，分別是烏茲別克斯坦境內的觀測站TASH00UZB(41.328 05，69.295 566 7，439.7)和觀測站KITG00UZB(39.133 386 4，66.886 738 2，620.631)，吉爾吉斯坦境內的觀測站BIK000KGZ(42.854 194 4，74.533 194 4，749.2)。

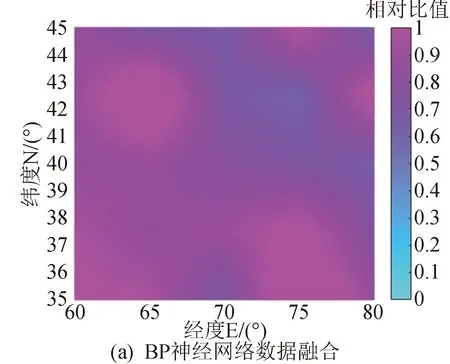
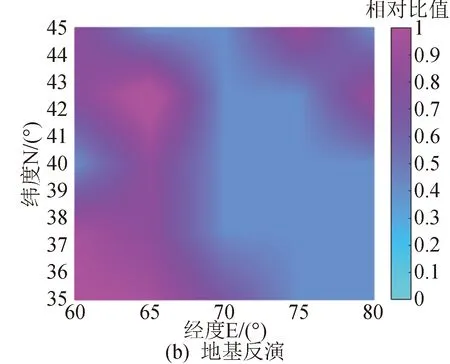
圖4 1月11日反演相對IGS的VTEC比值圖Fig.4 VTEC relative ratio map of inversions to IGS on January 11

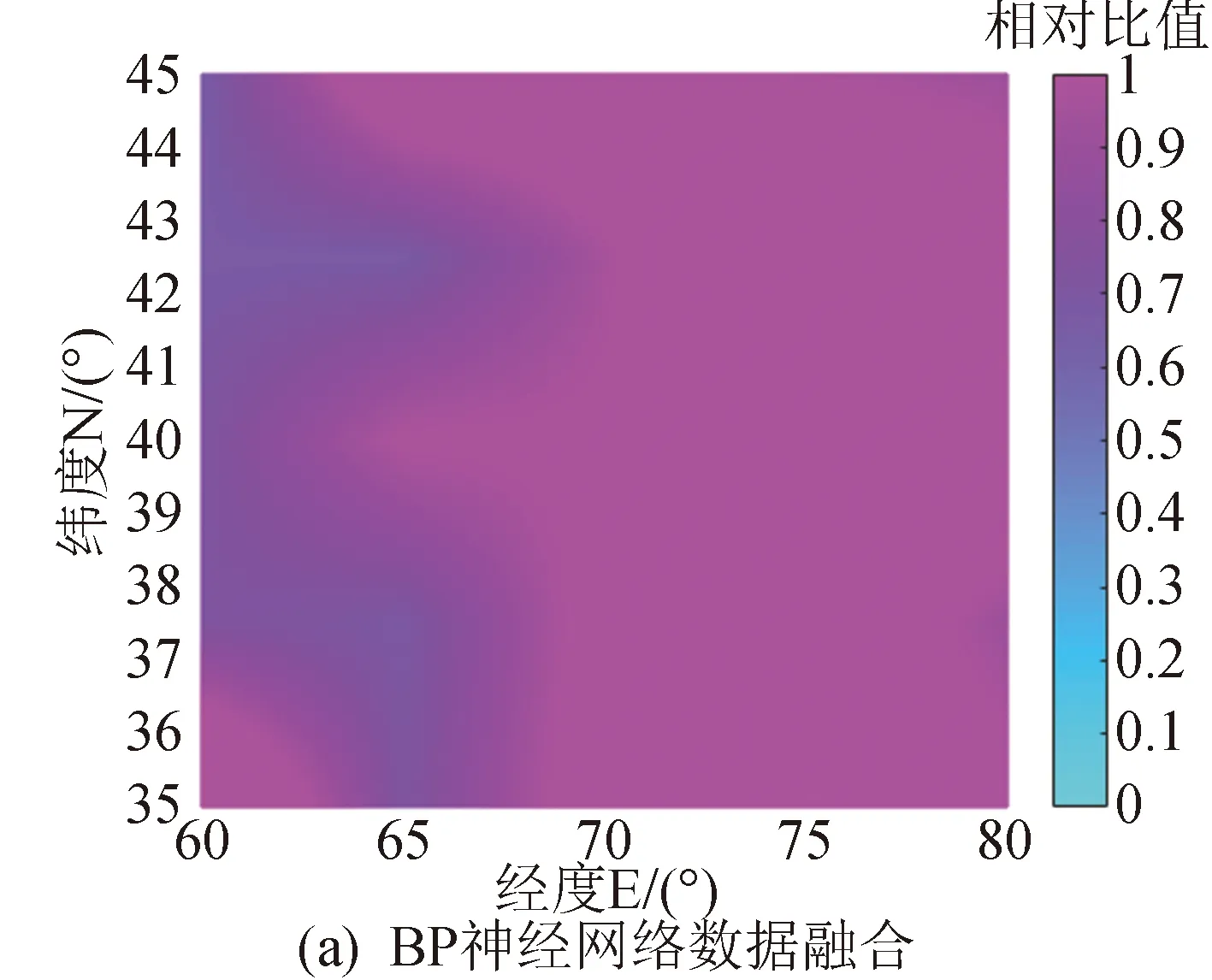
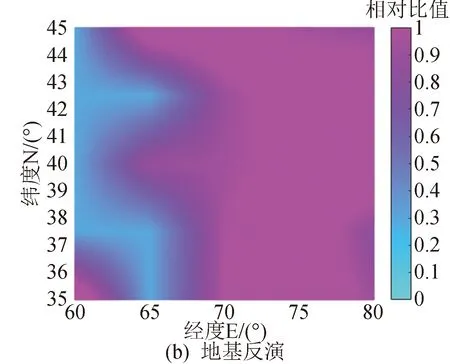
圖5 4月11日反演相對IGS的VTEC比值圖Fig.5 VTEC relative ratio map of inversions to IGS on April 11

圖6 7月11日反演相對IGS的VTEC比值圖Fig.6 VTEC relative ratio map of inversions to IGS on July 11

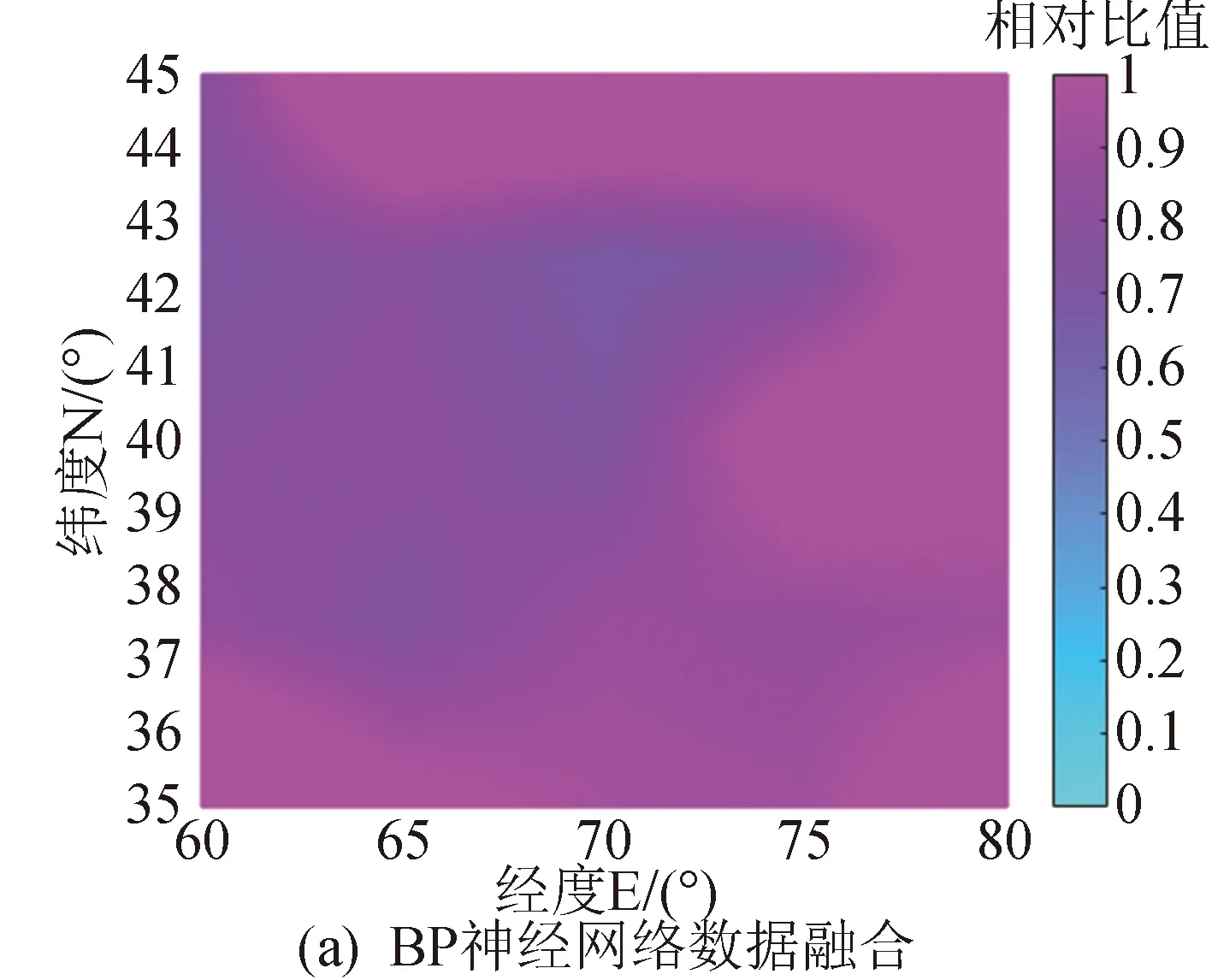
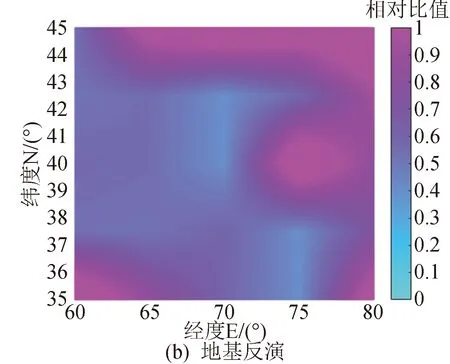
圖7 10月11日反演相對IGS的VTEC比值圖Fig.7 VTEC relative ratio map of inversions to IGS on October 11

從圖4～圖7可知，無論在春夏秋冬哪個季節，兩種方法都能獲得很好的反演效果，但基于BP神經網絡技術的數據融合比地基反演的結果更好，進一步提高了電離層反演精度。

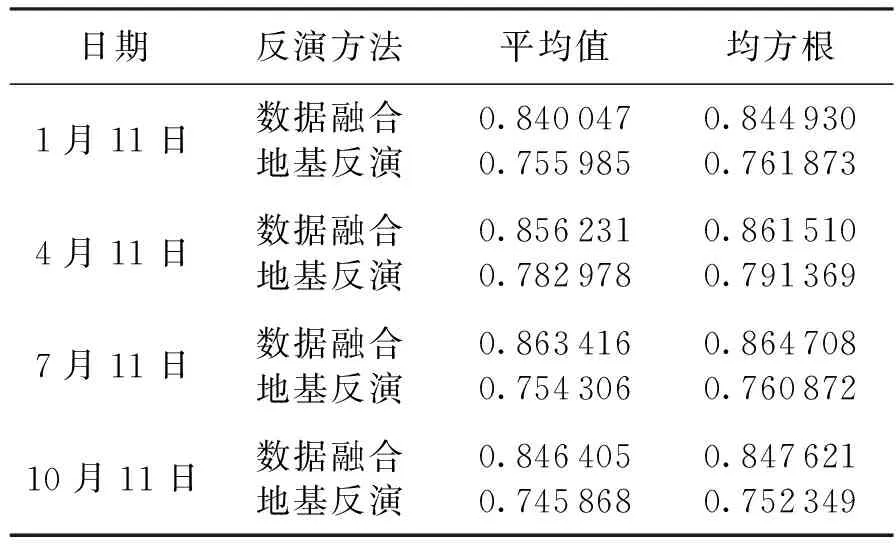
表1 反演效果評價標準

從表1可以看出，BP神經網絡技術數據融合獲得的相對比值的平均值和均方根均大于地基反演方法，說明利用BP神經網絡技術的數據融合反演效果優于地基反演效果。

4 結束語

本文利用基于BP神經網絡技術將電離層電子含量數據融合，以IRI為背景模式，融合地基反演電離層數據。通過對溫帶地區[35°(N)～45°(N)，60°(E)～80°(E)]的烏茲別克斯坦和吉爾吉斯坦境內的3個觀測站進行電離層反演，試驗結果表明，基于BP神經網絡的電離層數據融合和地基反演方法獲得電離層反演效果均比較好，但基于BP神經網絡技術的電離層VTEC融合效果更好，電離層反演精度更高，基于BP神經網絡技術的數據融合方法能夠在觀測站較少的情況下仍然可以獲得高的電離層反演精度。