直線與平面垂直教學設計
陽青柏
教學目標:
(一)教學知識點:1.直線和平面垂直的定義(通過觀察、探索、類比引出)。2.直線和平面垂直的判定定理(直觀感知并操作確認、證明不作要求)。3.直線和平面垂直的性質定理(直觀感知、操作確認、思辨論證、歸納并證明)。
(二)能力訓練要求(重要數學思想的滲透):1.轉化思想:空間問題轉化為平面問題是處理立體幾何問題的重要思想。空間中線線位置關系與線面位置關系的互相轉化。2.類比思想:研究線面平行時研究了定義,判定定理和性質定理,類比研究線面垂直。3.培養數學思維過程。
教學重點:直線與平面垂直判定與性質、數學思想的滲透。
教學難點:
性質定理的證明(反證法引入)、數學思想的滲透。
主要教學方法:
啟發誘思、實驗操作。
啟發誘導學生正確認識:“任意一條直線”“一個平面內兩條相交直線”正確尋求性質定理的證明思路,清楚直線、平面滿足何種條件就具有垂直關系。
教學過程:
一、引入課題
回顧直線與平面平行的研究思路,類比直線與平面垂直的研究
二、創設情境,引入新知
由生活中的實例引入,由前面學習的正投影和圓錐軸與底面垂直的形象,讓學生直觀感知直線與平面垂直的形象。
通過對圓錐軸與底面圓內的任意一條直線垂直關系的研究,師生共同總結直線與平面垂直的定義。
三、抽象概括直線與平面的定義
理解垂線、垂面、垂足的概念,掌握直線與平面的畫法與符號表示。熟悉定義的雙重功效,初步體會定義對于垂直關系的轉化作用。
四、定義的應用
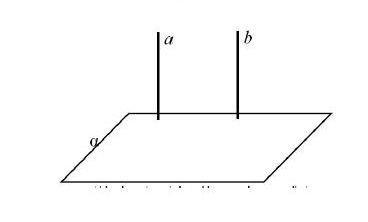
例1、(P36例1)求證:如果兩條平行線中的一條垂直于一個平面,那么另一條也垂直于這個平面。
已知:a∥b,a⊥a,求證:b⊥a
五、操作確認直線與平面垂直的判定定理
問題:直線與平面內一條直線垂直?兩條?無數條?(學生動手操作,直觀感知)
通過三角形折紙實驗操作,讓學生自主探究直線與平面垂直的判定定理。
六、判定定理
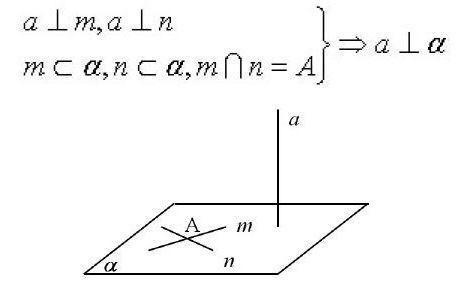
如果一條直線與一個平面內的兩條相交直線垂直,那么這條直線垂直于這個平面。
用符號語言表示這個判定定理的條件和結論
七、性質定理
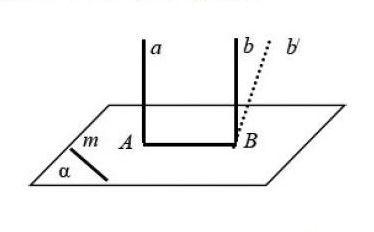
如果兩條直線垂直于同一平面,那么這兩條直線平行。
抽象為數學問題,已知:a⊥a,b⊥a,求證:a∥b
性質定理可以用來證明線線平行,也給出了空間中的平行關系與垂直關系的一種聯系。
它的證明思路是把空間中的問題轉化為平面問題來解決。
八、今天這節課,你學到了什么?有哪些收獲?(學生說,老師補充)

