融通算術教學 發展代數思維

○夏小進

運算教學在小學數學教學中占有重要地位。運算遵循一定的法則，按照一定的步驟，經歷較長時間的數量加工與操作求得答案，這個過程是程序性的，體現的是算術思維。而代數思維是由關系或結構來描述的，它的目的是發現（一般化的）關系，明確結構，并把它們連接起來，是表征和分析數量關系、解決問題、陳述和證明一般規律的有效途徑。

盡管《義務教育數學課程標準（2011年版）》已將“數與代數”設置為獨立的學習領域，并對小學代數課程內容進行了清晰的表述，但算術和代數之間的一致性和整體性仍未盡如人意。如何在算術教學中培養學生的代數思維，實現算術教學與代數教學的有效銜接與融通？這是小學數學教學必須正視、思考和解決的問題。我們可以從以下幾個方面展開思考。

一、在觀察中感悟代數思維的結構性

小學算術中蘊含著不少代數思維的素材，在低年級就可以適時向學生滲透一定形式和層次的代數思維。教師要引導學生用代數的眼光觀察算術問題，關注算術中的結構，思考、識別、提取包含于其中的關系，感受其中結構的變換和表達。

例如下面這道題，在□里填上合適的數。

以第一個算式為例，有兩種思考方法：第一種方法是先計算等號左邊，再依據“除數=被除數÷商”算出右邊方框里的數，體現了算術思維的程序性；第二種方法則從整體上觀察分析，36縮小4倍后是9，要想得數相等，右邊方框里的數應該是24縮小4倍后的結果，從而快速得出答案6，避免了繁瑣的計算，體現了代數思維的結構性。

這道題根據“商不變”“和不變”“差不變”“積不變”規律，引導學生從對數量的加工與操作轉向對算式結構的探討，從算術練習轉向了代數學習，提升了思維水平，并能有效推動后續學習，如分數的約分、比的化簡等。

二、在探尋中體悟代數推理的實用性

代數推理要求較高的抽象思維能力和演繹論證能力，具有豐富的思維訓練價值，有助于培養學生思維的嚴謹性，促進小學生從具體形象思維向抽象邏輯思維過渡。小學高年級算術教學可以提供適當的機會，引導學生用代數的思維思考算術問題，探尋蘊藏其中的代數關系和結構。

例如，在學習與倍數相關的內容時，呈現下列算式，要求學生先筆算。

教師可以設計如下的教學流程——

小結：學生算完后總結這些數都是4的倍數。

提問：仔細觀察這些數，它們有什么共同之處？

預設：這些數的末兩位都是4的倍數。

猜想：一個數的末兩位是4的倍數，那這個數本身也一定是4的倍數。

啟發：你能證明這一猜想嗎？

驗證：兩位以上的自然數，我們都可以用（100x+ab）來表示，其中ab就是它的末兩位，因為100是4的倍數，所以100x也一定是4的倍數，如果ab是4的倍數，那么它們的和（100x+ab）也一定是4的倍數。

這種規律的探尋過程既有合情推理，又有初步的演繹推理。學生在觀察、猜想、歸納、證明的過程中不僅獲得了數學知識，發展了代數推理能力，也培養了嚴謹的理性精神和科學態度。

三、在分析中領悟代數表達的多樣性

代數知識可被展示為言語表征、直觀表征（動作、實物和圖畫等）、符號表征等多種形式，每種表征都反映了某一方面的特征。借助多元表征有利于學生從多角度展開數學探索，既豐富了對數學的理解，又豐富了問題解決的策略。教師應創造機會引導學生用代數的語言從多角度表達算術問題，培養代數思維，發展學生的思維能力。

例如，計算：1005×2004-1004×2005。

由于直接計算特別繁瑣，教師可以引導學生從整體上觀察這個算式，嘗試從多角度分析、表征算式的結構，發展代數思維，加強數學理解。

表征一：字母符號表征

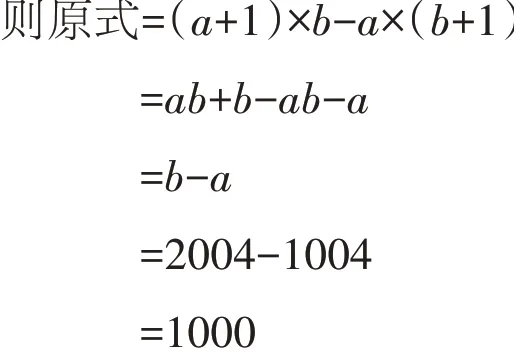
表征二：圖形表征

把1005×2004表征為長方形AEFG的面積，1004×2005表征為長方形ABCD的面積。于是原式就被表征為求長方形AEFG與長方形ABCD的面積之差，也就是求長方形DHFG與長方形EBCH的面積之差，容易看出長方形DHFG與長方形EBCH的 寬 都 是1，所以兩者之差為：2004×1-1004×1=1000。

四、在對比中體會代數方法的優越性

算術方法是設法通過已知量求出未知量，在此過程中未知量被置于特殊地位，學生是逆向思維解題。如果題干中有多條信息且彼此存在復雜關系時，學生難免會產生一些困惑，從而產生解題障礙；而用代數方法解題屬于順向思維，先用字母代替未知數，等于增加了一項條件，未知量和已知量均參與運算，這就可以順利建立等量關系。隨著學習的深入，問題難度逐漸加深，代數方法的優勢越發明顯。教學中應加強學生對代數方法的學習、理解與運用，使學生意識到算術方法的局限性，從而自發產生代數學習的動力和興趣。

例如，這道題：某工廠生產A、B兩種商品，生產的A商品比B商品少12件。已知B商品全部合格，而A商品只有合格，兩種商品合格的共有57件，兩種商品各生產了多少件？

用算術方法解決這個問題需要較多的逆向思考和較復雜的解題技巧；而用代數方法（方程）可以根據題意正向建立等量關系式：合格的A商品數+合格的B商品數=57件。設生產A商品x件，則生產B商品（x+12）件，列方程為=57。從而簡化解題過程，順利解出答案。

綜上，教師應引導學生意識到代數思維的優越性，讓代數思維方式成為學生的內在需要，促進學生從算術思維向代數思維的跨越，為小學和初中數學學習內容的有效銜接搭建橋梁。