數學課堂節奏與調控教學案例
車紅妮
課堂節奏指的是一節課的張馳快慢及其有規律的變化。課堂教學節奏把握得好壞,直接影響教學效果。因此,在課堂教學中教師應根據教材特點和學生實際,調控好課堂節奏,自始至終牽動學生的注意力,維系學生的學習熱情,使學生在和諧優美的節奏中快樂主動地學習,身心得到全面的發展。
下面將高中數學教學中的案例展示出來,與大家分享,有不足之處,請各位批評指正。
案例:函數的極值
本節內容是在利用導數研究函數單調性基礎上,進一步研究函數極大值和極小值,是導數在研究處理函數性質問題中的一個重要應用。
重點:利用導數求函數極值
難點:函數的極值與導數的關系
疑點:(1)函數極值的理解;(2)導數f′(x)=0時,x不一定是極值點。
教法:以自主探究,合作交流法為主,講授法、啟發法等為輔。
(一)知識回顧
函數的單調性
在(a,b)內可導函數f(x),f′(x)在區間(a,b)內不恒等于0,則
f′(x)≥0?f(x)在區間(a,b)上是? ______?? ;
f′(x)≤0?f(x)在區間(a,b)上是 ______???? .
【設計意圖】復習上節課所學知識,為學習新知做鋪墊。先提問個別學生,再全體回答。
(二)自主探究
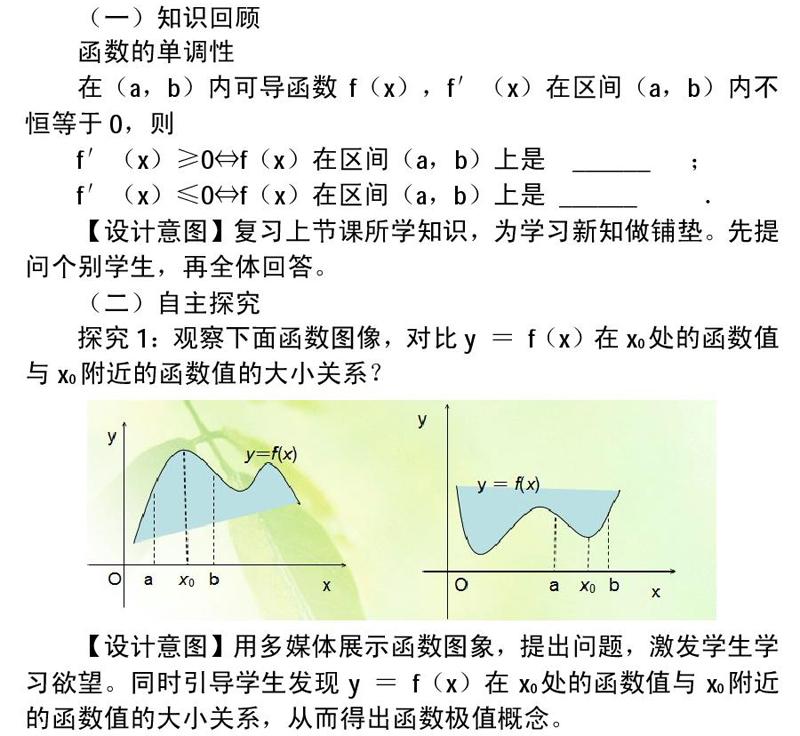
探究1:觀察下面函數圖像,對比y = f(x)在x0處的函數值與x0附近的函數值的大小關系?
【設計意圖】用多媒體展示函數圖象,提出問題,激發學生學習欲望。同時引導學生發現y = f(x)在x0處的函數值與x0附近的函數值的大小關系,從而得出函數極值概念。
1.函數的極值
(1).極大值;(2).極小值;(3).極值
【設計意圖】學生試著總結極大值,極小值概念,教師及時補充。不僅提高了學生觀察能力,識圖能力,語言表達能力;而且培養了學生遇到問題,自主解決的習慣。
思考:
(1)極值點與極值的區別?
(2)極值是函數的整體性質,還是局部性質?
(3)函數極值唯一嗎?
(4)極大值一定比極小值大嗎?
【設計意圖】設置問題,采取分組討論,合作交流的方式,進一步加深對概念的理解。也突破了本節課的第一個疑點。
探究2:極值與導數有什么關系?如何用導數判別函數的極值?
【設計意圖】再次觀察函數圖像,發現極值處兩側函數的單調性不同,從而歸納出判斷函數極值的方法。
2.判別極值的方法
【設計意圖】學生試著總結判別極值的方法,教師及時補充。增強了學生自主探究的信心,提高了學生學習的積極性。
思考:函數f(x)=x3在x=0處有極值嗎?
【設計意圖】設置問題懸念,使其熱情高漲。采取分組討論,合作交流的方式,重在突破本節課的第二個疑點。
探究3:如何求可導函數的極值?試通過例題的解答總結。
[例1] 求函數f(x)=2x3-3 x2-36x+5的極值
3.求可導函數的極值的步驟
【設計意圖】通過動手實踐,將所學知識加以應用,并總結求函數的極值的步驟。提高了學生總結歸納的能力,知識應用能力。
(三)鞏固訓練
求函數f(x)=3x3-3 x+1的極值。
【設計意圖】進一步掌握求可導函數的極值的方法步驟。
(四)課時小結
(1)通過本節課的學習,我們學到了哪些知識?
(2)我們是怎樣學習利用導數求函數極值的?
【設計意圖】讓學生自己小結本節課的學習內容,采用回顧的方式,不斷總結,不斷補充。
(五)跟蹤練習
下列各點是函數f(x)=1+3x-x3的極值點的是(?????? )。
A. x=0????? B. x=1????? C. x=2????? D. x=3
(2)求f(x)=x - ㏑x的極值。
【設計意圖】通過訓練,檢測學生對所學知識的理解和掌握。
(六)作業布置
課本62頁 練習,習題3-1組3題
教學過程節奏:
1. 復習回顧所學導數與函數單調性知識。(一般占用3分鐘)
2. 觀察函數圖象得出關于函數極值的相關結論。(一般占用25分鐘)
3. 鞏固訓練(一般占用5分鐘)
4. 課時小結(一般占用2分鐘)
5. 跟蹤練習(一般占用8分鐘)
6. 作業布置(一般占用2分鐘)
案例分析:
反觀整個教學過程,對于已學過的知識,通過復習喚起學生回憶,一般占用3分鐘的時間。重點放在本節課的內容,對于新的內容和學生學習中存在的難點和疑點采用自主探究和合作交流的方法,通過觀察函數圖象引導學生識圖獲得具體明確的感性認識,設置問題加深對概念規律的理解,在此基礎上讓學生學習提出問題、分析問題和解決問題的方法。雖然每個環節都是精心設計的,每道例題都是認真挑選的,但是學生必須全神貫注步步緊跟,否則就要掉隊。一節課下來,所有學生均有如釋重負的感覺。究其原因,這節課的速度太快,知識容量略大,以致不能很好地控制時間甚至是出現拖堂的情況,這樣會降低課堂教學效果。

