相場模型及其在電化學儲能材料中的應用*

張更 王巧 沙立婷 李亞捷? 王達 施思齊

1) (阿卜杜拉國王科技大學物理科學與工程系， 圖瓦， 沙特阿拉伯 23955-6900)

2) (上海大學材料基因組工程研究院， 上海 200444)

3) (上海大學材料科學與工程學院， 上海 200444)

隨著計算機技術的快速發展， 計算研究在探究材料體系微結構演化方面展示出巨大的優勢. 作為材料動力學的一種計算研究方法， 相場模型不僅可以避免復雜的界面追蹤， 而且便于處理各類外場因素， 因而受到廣泛關注. 藉此本文介紹了相場模型的理論框架以及目前主流的多元多相系相場模型： Carter 模型， Steinbach模型和Chen 模型， 并從相場變量的解釋、耦合熱力學數據庫的方式、體系自由能密度的構建方式以及演化方程等方面對上述三個模型進行了系統地概括和比較. 進一步， 聚焦于相場模型在各向異性輸運和相分離、彈性和塑性變形、裂紋擴展和斷裂、枝晶生長機制等方面的應用， 系統展示了相場模型在描述電化學儲能材料微結構演化以及改進其性能方面的巨大潛力. 最后， 從相場模型的理論改進和應用拓展兩個方面， 討論并展望了電化學儲能材料相場模擬的未來發展方向和亟待解決的關鍵問題.

1 引 言

在能源危機和環境污染日益嚴重的背景下， 發展綠色可再生能源是社會發展的必然趨勢. 太陽能、風能等可再生能源發電具有不穩定、不連續、不可控等特點. 大規模儲能系統可有效進行可再生能源發電的調幅調頻與平滑輸出， 實現能源跨越時間和空間的分配調節， 對可再生能源的生產和消費具有革命性意義. 電化學儲能是當前主要的儲能技術之一， 主要的電化學儲能設備包括鋰離子電池、鉛酸電池和超級電容器等， 具有使用方便、環境污染少、不受地域限制和能量轉化效率高等特點. 提高電化學儲能材料的能量/功率密度、循環壽命和安全性能， 是當前主要的研究方向， 而建立能夠反映電化學儲能體系基本物理化學機理的模型， 對開發高效安全的電化學儲能材料具有重要意義[1]. 隨著計算機技術的飛速發展， 模擬研究越來越多地受到科研工作者的青睞. 在建立可靠的模型并設計優良的數值算法的前提下， 可以節約人力物力地高效開展研究. 模擬研究不僅有助于了解材料的微觀組織結構演化， 還可以根據預測結果設計材料、探索材料組分、加工方式等與材料性能之間的聯系. 到目前為止， 模擬研究方法已經涵蓋了廣泛的時空尺度， 包括密度泛函理論(density functional theory，DFT)[2，3]、分子動力學(molecular dynamics， MD)[4]、蒙特卡洛(Monte-Carlo， MC)[5]、有限元分析(finite element analysis， FEA)[6]和相場模型(phase-field model， PFM)[7]等.

相場模型是一種基于熱力學來研究材料微結構演化的模擬研究方法. 與DFT， MC， MD 和FEA 等方法相比， 相場模擬在微觀和宏觀模擬之間架起了橋梁， 是描述和預測材料微結構演化的有力計算方法[7]. 在熱力學中， 相是性質均勻穩定的空間結構， 場是時空變量的函數， 相場即為用時空變量的函數來描述材料的微結構演化. 相場模型的一個重要特點是擴散界面， 斯洛文尼亞物理學家Stefan 在19 世紀80 年代提出處理相邊界問題的尖銳界面方法并廣泛用于解釋擴散相變動力學[8].求解尖銳界面模型需要相邊界處的銜接條件， 這需要對相邊界進行追蹤. 但在實際問題中， 相邊界的形狀和運動往往十分復雜， 這導致求解尖銳界面模型的演化方程極其困難. 相場通過引入擴散界面模擬解決了這一問題， 圖1 顯示相變界問題中的尖銳界面和擴散界面的對比. 相場模型引入相場變量來標度相態， 其演化直接反映相變過程， 無需追蹤界面， 這大大降低了問題的復雜性. 相場模型的另一特點是處理外場的便利性. 若體系除了相變以外還有濃度、溫度、外加電磁場等參與， 則還需引入其他場變量來描述體系的狀態. 所有描述體系的場變量構成完備場變量集， 它們可以構建出體系的自由能泛函. 場變量的演化方程可依據自由能最小化原理[9]和局域平衡原理[10]導出， 它們通常為非線性偏微分方程. 相場模型中的外場被視為對總自由能的一部分貢獻， 其對體系微結構演化的影響可以通過其對自由能的影響體現出來. 通過數值求解演化方程得到場變量在模擬區域和時間節點上的值， 便可得出材料體系的微結構演化. 可以看出， 相場模型對材料體系的描述方法與Maxwell 理論對電磁場的描述方法完全一致， 所以本質上相場模擬是經典場論思想在材料科學中的應用. 然而目前的相場模型也存在不足， 對于二相系， 大部分模型都相當成功， 但拓展到多相系時， 目前的相場模型具有數學處理不嚴謹或物理描述不自洽等問題. 過去的三十年中， 相場模型在模擬材料微結構演化方面發揮了重要作用. 最初的相場模型用來研究二元合金的凝固[11]， 發展到今天， 涉及材料力學和熱力學性能的大部分微觀過程都由此得到了比較深入的研究，如晶粒生長[12]、枝晶生長[13]、形核[14，15]、析出[16，17]、燒 結[18，19]、位 錯[20，21]、彈 性[22，23]、塑 性[24，25]和 斷裂[26，27]等.

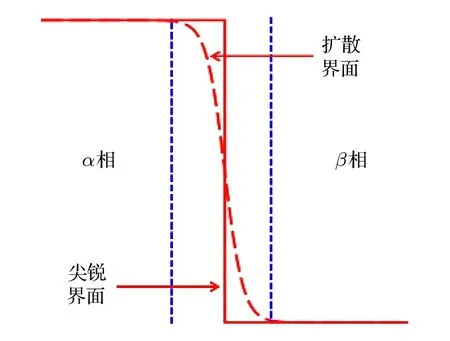
圖1 相變界問題的尖銳界面和擴散界面的對比Fig. 1. Comparison between sharp and diffusive interfaces for phase boundary problems.

2 相場理論框架及關于目前主要相場模型的評述

2.1 相場模型的理論框架

本文中約定： 當相指標和組分指標都出現時，相指標為上標， 組分指標為下標； 當相指標和組分指標單獨出現時， 它們均為下標. 在相場模型中，最基本的場變量是描述相態的相場變量φα(α=1,··· ,n). 在不同的模型中相場變量的含義不盡相同， 但是由于相可以生成或消失， 相場變量都被當作非守恒變量， 它們遵循Allen-Cahn 方程[28]：

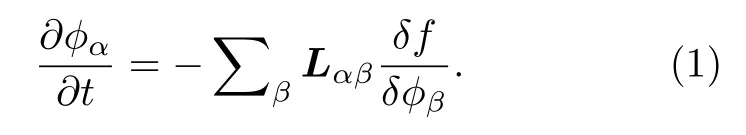
一般體系都需要引入描述組分的濃度變量ci(i=1,··· ,m). 在沒有化學反應的前提下， 濃度變量被當作守恒變量. 它們遵循Cahn-Hilliard 方程[29]：

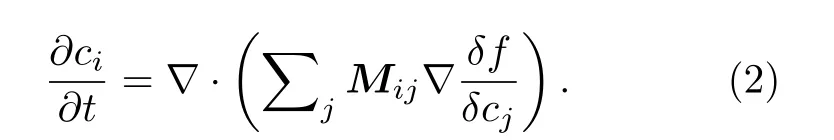
方程(1)和方程(2)中， (Lαβ)n×n為界面遷移率矩陣， (Mij)m×m為組分的移動性參數矩陣， 它們均為半正定矩陣，f為體系的自由能密度，稱為變分導數. 與普通導數相比， 變分導數還包含了場變量梯度的貢獻.

事實上， 上述兩個方程都是自由能最小化的表達. 設描述體系的完備場變量集為{ui,?ui}， 則體系的自由能泛函可以表達為

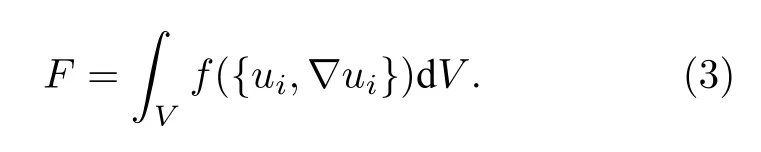
固定邊界條件(邊界條件的改變意味著研究問題的改變)， 對上述方程關于時間求導得

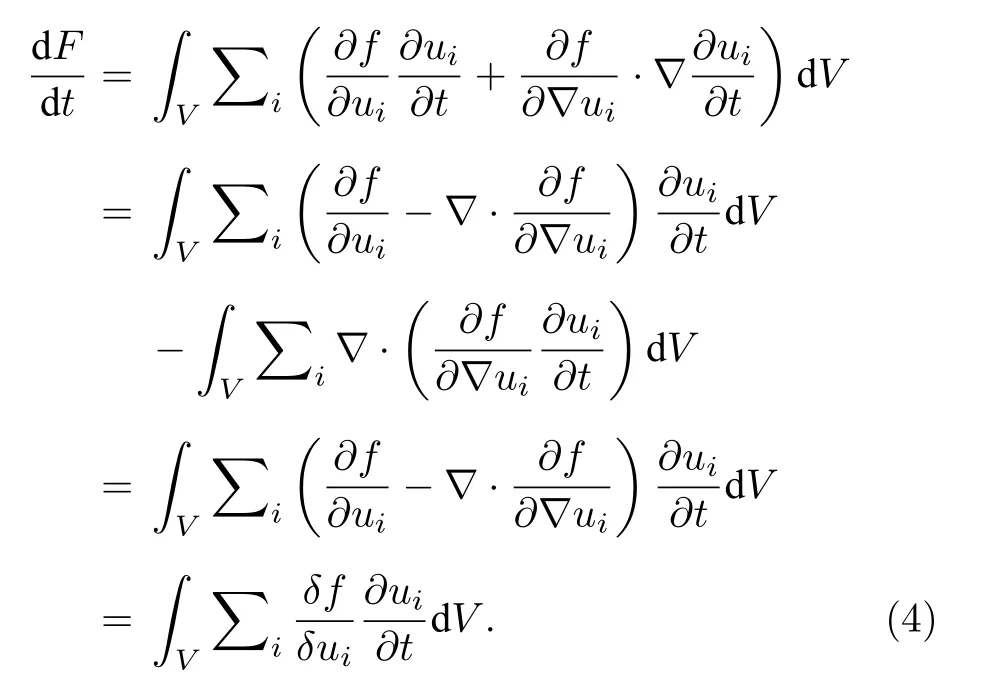
將方程(1)和方程(2)分別代入上述方程得到：

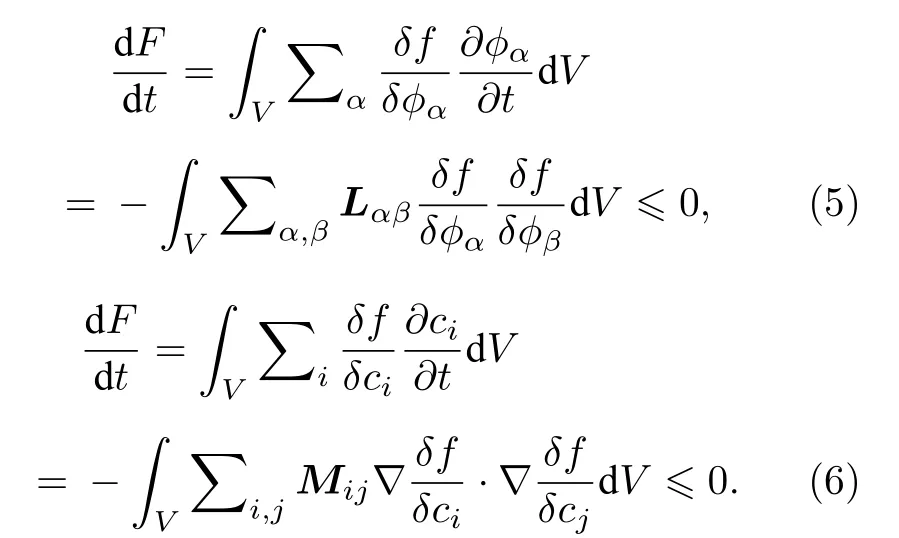
方程(1)和方程(2)是相場模型的基礎， 不同的相場模型是指濃度描述方式和總自由能密度表達方式的差異.

2.2 常見相場模型及其特點

相場模擬通常分為三個層次： 第一層次描述材料體系的微結構演化， 是定性、半定量、定量研究的混合； 第二層次分析材料的微結構和宏觀性能的關聯， 根據研究體系的模擬結果預測其性能， 是半定量、定量研究的混合； 第三層次消除模擬中可調參數， 通過理論計算和實驗測量確定所有模擬參數， 進一步通過調控體系的物理環境改進和控制體系的性能， 是完全的定量研究. 不管是哪種層次的模擬， 都需要精準的熱力學數據庫來識別所研究的體系. 在計算熱力學中， 體系的熱力學數據庫是由相濃度(相摩爾分數， 本文用y表達)來構造的， 但是擴散動力學只表達總濃度(總摩爾分數， 本文用c表達)的演化方程——Fick 擴散方程. 所以， 要實現熱力學數據庫與相場模擬的耦合主要有以下兩種方式： 1) 采用總濃度的演化方程， 將求解得到的總濃度以一定的方式分解為相濃度與熱力學數據庫對接， 代表為KKS 模型[30]； 2) 直接構造相濃度的演化方程與熱力學數據庫對接， 代表為Steinbach模型[31，32]. 耦合熱力學數據庫的方式， 相場變量的解釋， 體系自由能密度的構建方式以及演化方程等要素一起區分了不同的相場模型. 由于二相系模型是多相系模型的特例， 故這里只討論多相系(兩相及以上)模型， 包括當前主流的Carter 模型、Steinbach 模型和Chen 模型. 下述討論中， 假定體系存在n個相，m個組分，fα為α相的自由能密度.有時為了更細致地區分一個相(通常是固相)的不同狀態， 需要用多個相場變量去描述該相， 例如晶粒的不同取向. 此時可將該相的不同狀態視為若干個更精細的“亞相”， 每個“亞相”引入一個相場變量， 意味著一個相(普通意義)可以用若干個相場變量描述. 為了表述上的方便， 下述討論中， 每個相(“亞相”意義)引入一個相場變量描述體系的相態.

2.2.1 Carter 模型

在Carter 模型中， 相場變量被解釋為相分數，滿足歸一化條件， 即總濃度以相同的值分配到各個相， 即組分i在每個相中的相濃度都相同， 等于總濃度. 該模型使用如下的自由能密度[33]進行描述：

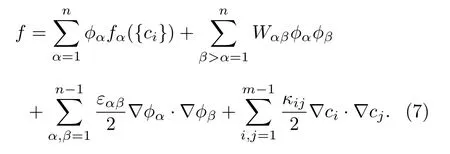
上式中Wαβ為勢壘高度，εαβ和κij分別為相場和濃度的梯度能系數， 它們均為模型的唯象參數. 方程(7)表達的自由能密度具有非常明晰的物理意義：右邊前兩項只與場變量有關， 稱為均勻自由能密度， 它包含兩部分： 各相自由能密度的加權平均相間勢壘后兩項與場變量的梯度相關， 稱為非均勻自由能密度， 也包含兩部分： 相場梯度的貢獻和濃度梯度的貢獻

Carter 模型的相場變量和濃度變量的演化方程分別為

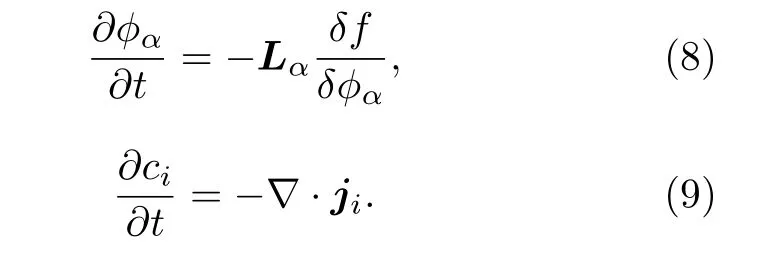
容易看出， 方程(8)是方程(1)的特殊情形，它滿足自由能最小化原理. 該模型的演化方程形式簡單， 計算復雜度較低， 編程求解時比較方便. 但是相場方程與相場變量的歸一化條件不相容， 這意味著獨立相場變量的不同選取將影響模擬結果， 然而真實材料體系的微結構演化是一個確定的過程，它應該與對體系的描述方式無關. 在實際求解中需要數值截斷和重整化來確保每一個相場變量都在區間[0， 1]中， 盡管這些處理對模擬效率影響甚微，但卻喪失了數學上的合理性和嚴謹性.

2.2.2 Steinbach 模型

同Carter 模型一樣， Steinbach 模型的相場變量也被解釋為相分數， 并區分了相濃度和總濃度ci， 用相濃度來構造相能量密度. 其自由能密度為[31]

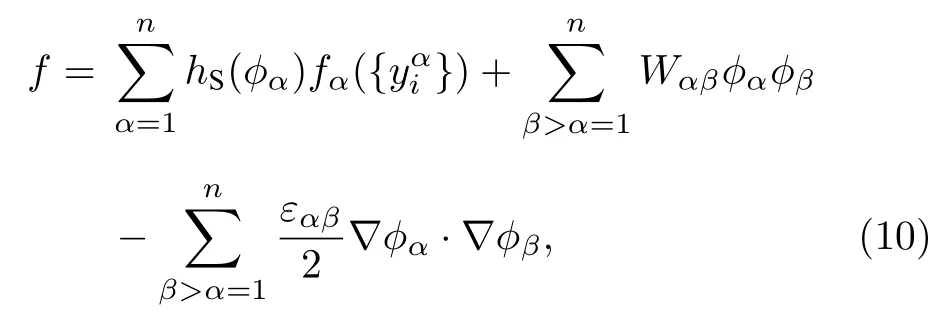
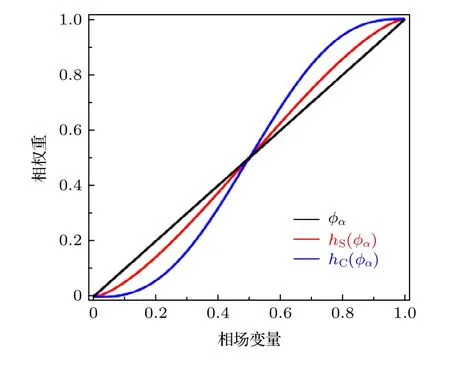
圖2 相場變量與Steinbach 模型、Chen 模型中的相權重函數的比較Fig. 2. Comparison of phase field and phase-weight functions in Steinbach and Chen models.

Steinbach 模型的相場方程和相濃度方程分別為[31]

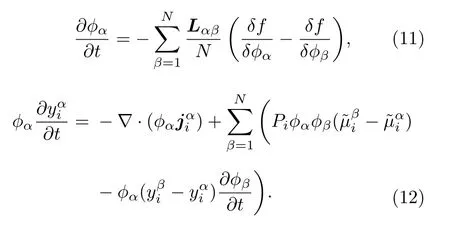
需要注意， 上述兩方程中的N是局域相數， 與上面自由能密度表達式中n(整體相數)是不同的.該模型的相場方程不僅滿足自由能最小化原理， 而且還與相場變量的歸一化條件相容， 這意味著該模型的模擬結果與獨立相場變量的選取方式是無關的. 為了便于耦合熱力學數據庫， 該模型第一次構造了相濃度的演化方程. 在Steinbach 模型之前，解決熱力學數據庫和總濃度方程對接的方法就是依據等化學勢原則將總濃度分解為相濃度， 這個思想由KKS 模型首先給出[30]. 隨著組元和相的增加，這種處理方法的計算量增加很快， 而且等化學勢原則對平衡、弱非平衡體系是適用的， 但不適用于強非平衡體系. 而Steinbach 模型依據演化方程來確定相濃度， 不僅大大降低了處理多元多相系的復雜性， 而且也適用于強非平衡過程， 如快速凝固. 雖然該模型克服了Carter 模型的與相場變量的歸一化條件不相容的缺陷， 但它也引入了其他問題. 方程(11)包含了不連續的量—局域相數， 這導致模擬結果違背近距作用， 即兩相即便不接觸也可能出現相互作用. 方程(11)是對體系相演化的局域描述(在φα=0 時，φα的演化方程沒有意義)， 在實際應用中， 需要根據一定的準則判斷相對于α相的鄰近界面區(包含： 界面和接近界面的體相)與非鄰近界面區. 對多相系而言， 相對于α相的相區判斷需要大量的計算， 這會降低模擬效率.

2.2.3 Chen 模型

與Carter 模型和Steinbach 模型不同， Chen模型中的相場變量被解釋為序參量， 它們只是相的標度， 沒有明確的物理意義. 該模型用總濃度ci描述組分演化， 用相濃度構建相自由能密度， 它用KKS 模型的處理實現總濃度方程與體系的自由能密度的對接， 即按照一定的原則將總濃度分解為相濃度. 其自由能密度為[19，34]

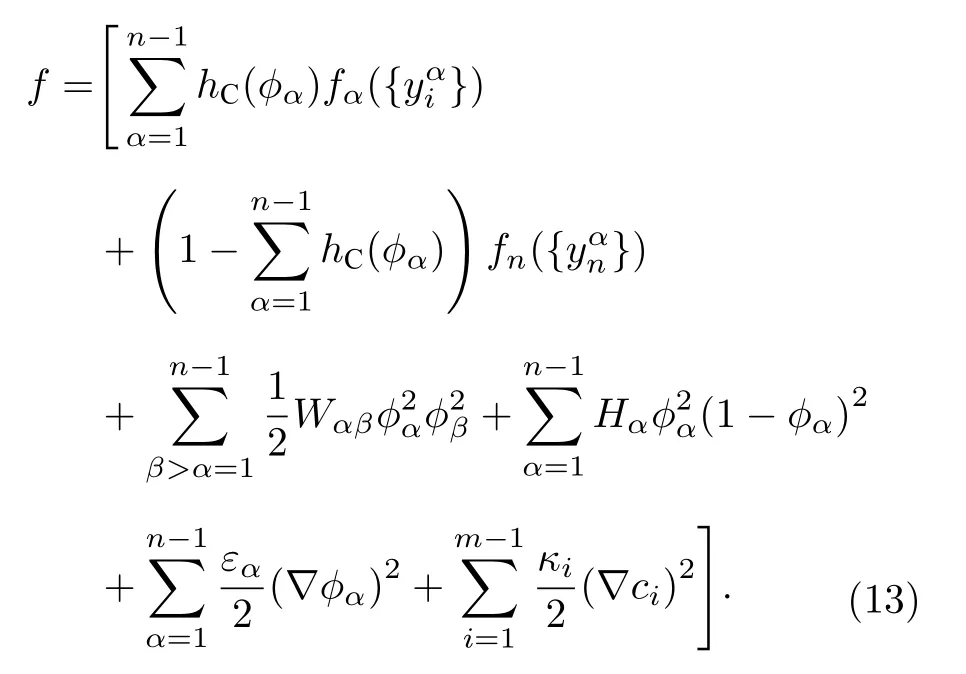
Chen 模型的相場和濃度方程形式與Carter模型的完全一樣， 但如上所述， 它們將總濃度分解成相濃度的方式是不一樣的. 由于方程(13)中的相間勢壘項在φα=0 和φα=1 時有最小值， 該模型的相場方程可以自動將相場變量約束在區間[0， 1]內， 即使數值求解不做截斷處理， 也可以得到符合物理事實的結果. 和Steinbach 模型相比， 該模型的相場方程是對體系演化的整體描述， 數值求解時無需相區判斷， 故模擬效率比較高. 由于該模型舍棄了相平權， 所以選取α為參考相與選取β為參考相的模擬結果在理論上存在差異. 事實上， 真實材料體系的微結構演化是一個確定的過程， 它應該與對體系的描述方式無關.

三種多相系的相場模型相比， 在模擬效率方面， Carter 模型最高， Chen 模型次之， Steinbach模型最低； 在耦合熱力學方面， Steinbach 模型最方便， Chen 模型次之， Carter 模型耦合真實數據庫會和相圖存在偏差； 在數學處理方面， Chen 模型的嚴謹性(可以不使用數值截斷和重整化處理得到合理模擬結果)比Steinbach 模型和Carter 模型高； 在相態描述方面， Steinbach 模型自洽性(模擬結果與參考相的選取無關)比Chen 模型和Carter 模型高； 在組分描述方面， 三種多相場模型都只有在摩爾體積與組分無關的情況下在物理上自洽(模擬結果與參考組元的選取無關). 盡管這三個多相場模型都有不完善的地方， 但從解決實際工程問題的角度來看， 上述相場模型在研究材料微結構演化方面均發揮了巨大的作用. 材料的微結構演化是一個極其復雜的動力學過程， 如果從一開始就苛求模型在數學上高度嚴謹， 在物理上高度自洽，那么相場理論可能就不會誕生或不能取得如此豐富的成果.

3 電化學儲能材料的已有相場模擬結果簡介

電化學儲能系統是一個十分復雜的體系， 充電和放電對應金屬陽離子在陽極和陰極之間的反復遷移， 這往往涉及多個組分的擴散和固態相變[35]，因而帶來了許多問題， 如各向異性輸運和相分離，彈性和塑性變形， 裂紋擴展和斷裂， 以及枝晶生長等等. 相場模型是解決這些問題的強有力的工具之一. 將相場方法應用于電化學儲能系統的最初嘗試是研究電極材料(如LiFePO4)在充放電過程中的相 分 離. Carcia 等[36]將Cahn-Hilliard 方 程 與Maxwell 方程耦合， 闡明了電磁活性體系的變分原理； Guyer 等[37，38]提出了模擬電化學界面的雙層和Butler-Volmer 動力學的相場模型； Han 等[39]利用Cahn-Hilliard 方程模擬了鋰離子在LiFePO4中的擴散行為. 以上工作被公認為相場模擬應用于電化學儲能材料的奠基工作， 啟發了科研工作者利用相場模型研究電化學儲能材料的各種微結構演化過程. 利用相場模擬研究電化學儲能材料微結構演化的一般步驟如圖3 所示.

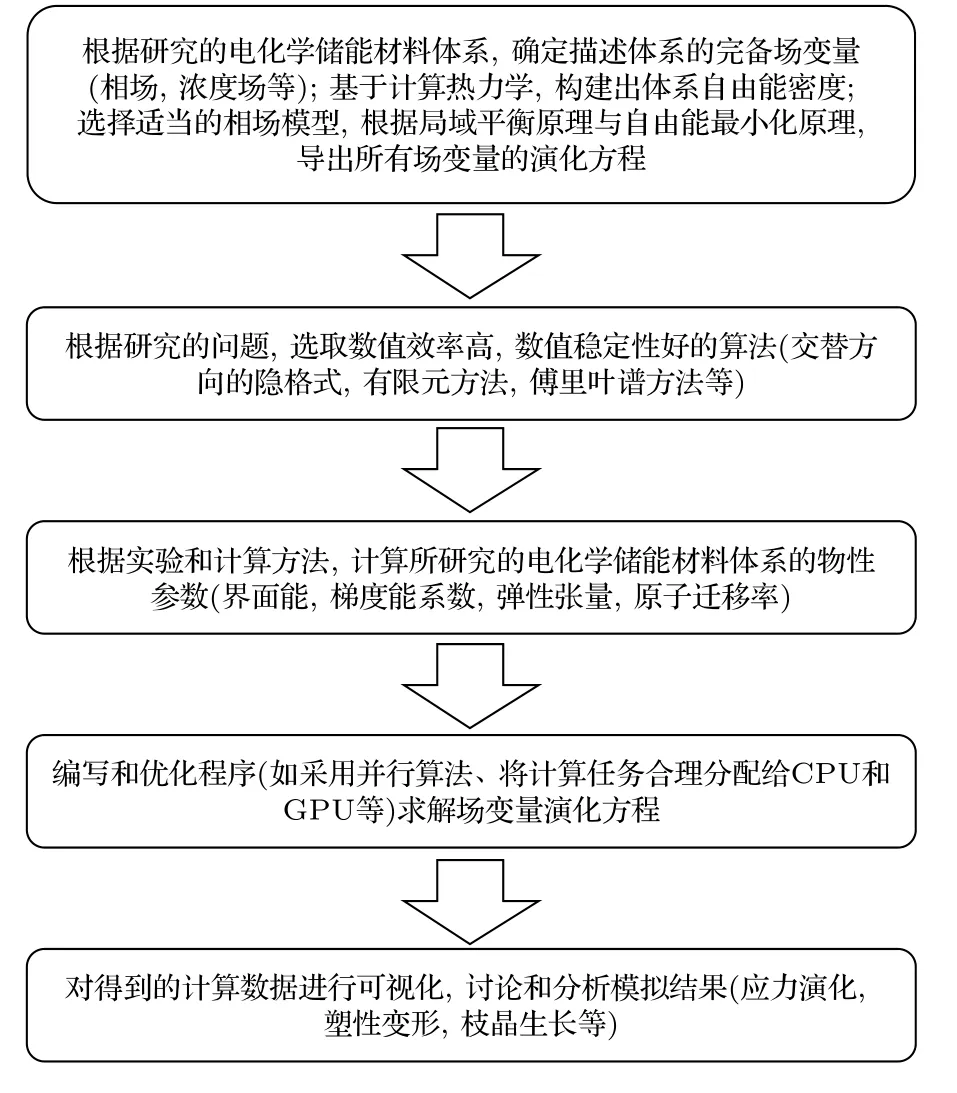
圖3 相場模型中研究電化學儲能材料微結構演化的步驟Fig. 3. Steps for investigating microstructure evolution of electrochemical energy storage materials in phase-field model.

3.1 電化學相場模擬中的化學反應、電場、彈性

由于電化學反應的存在， 相場和濃度的演化方程中考慮源項nα,i(單位體積和時間內組分i生成的物質的量)， 方程(1)和方程(2)相應修改為

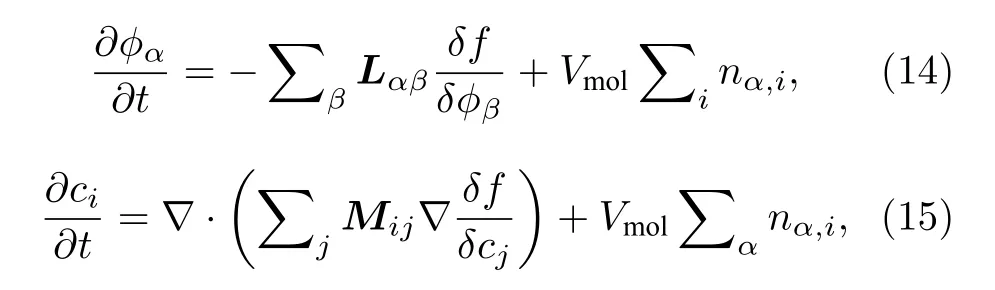
其中nα,i通常是電流密度、相場和濃度的函數.

將相場模型應用于電化學儲能材料體系， 總自由能密度中需要考慮電場的貢獻. 引入電勢場Φ來描述電化學儲能材料體系的電場， 則電場能密度felec可以表達為

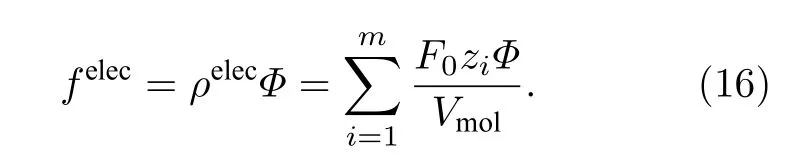
這里ρelec為電荷密度；F0為法拉第常數；zi為組分i的化合價；Vmol是系統的摩爾體積. 電勢場是描述電化學儲能材料體系的基本場變量， 其演化方程由電荷守恒定律給出：

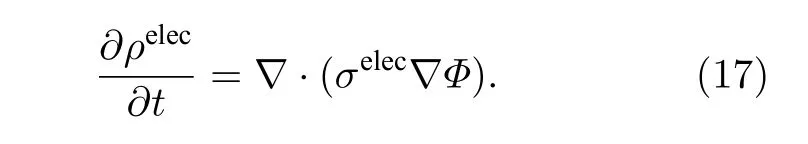
這里σelec為電化學儲能材料的電導率.

電化學儲能材料體系的力學性能涉及到彈性，此時總自由能密度中需要考慮彈性的貢獻. 引入應變張量ε描述電化學儲能材料體系的形變， 則felas可以表示為

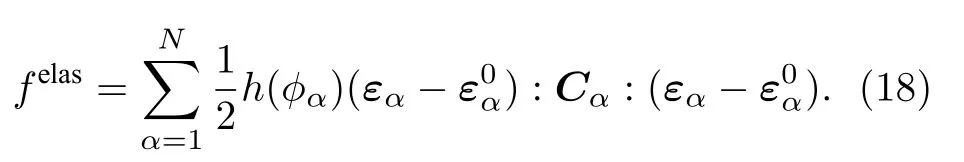
這里εα和分別為α相的總應變張量和本征應變張量，Cα為α相的彈性張量. 由于應力的弛豫時間遠遠小于相變和擴散的弛豫時間， 一般認為應力始終平衡， 故應變張量εα的演化方程為

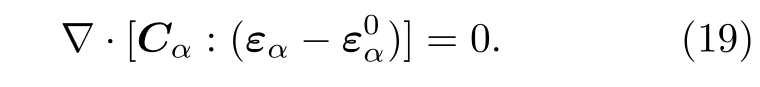
3.2 相場模型在電化學儲能材料中的應用

3.2.1 離子輸運和相分離

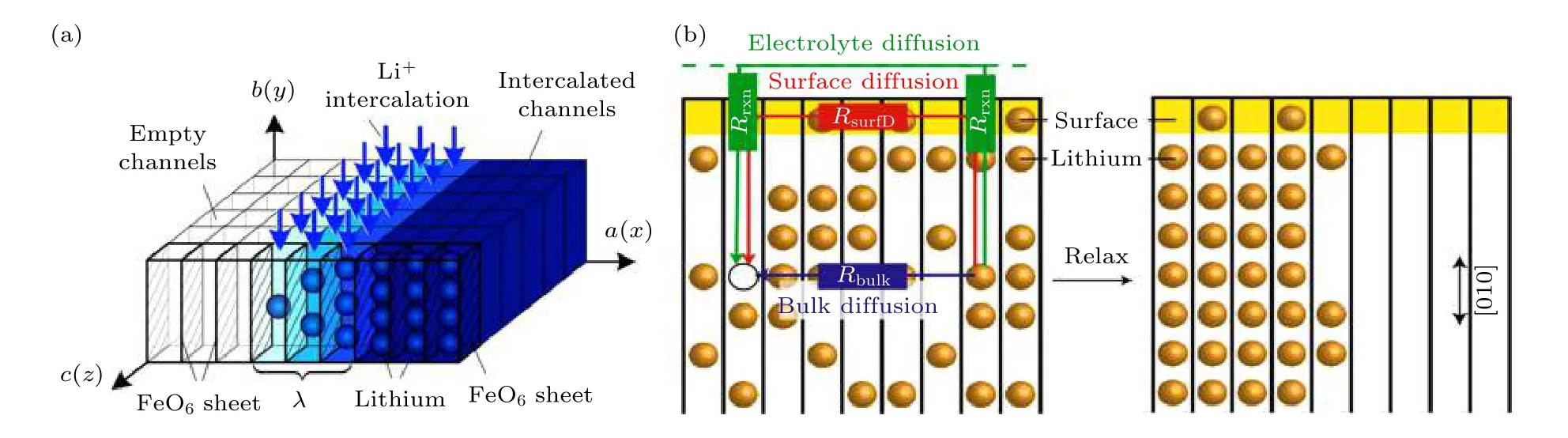
圖4 (a) 鋰離子嵌入到FePO4 時活躍面(010)快速擴散(藍色箭頭)和相分離示意圖[43]； (b) LiFePO4 相變過程中的三種可能的擴散路徑： 體擴散、表面擴散和電解液擴散[45]Fig. 4. (a) Schematic diagram of diffusion of active surface (010) (blue arrows) and phase separation when Li-ion intercalates FePO4[43]； (b) three potential migration paths in phase transition of LiFePO4： bulk， surface， and electrolyte diffusions[45].

在可充電電池中， 離子輸運對于正極材料電極容量、充放電效率和電池體系的循環性能等關鍵性質具有很大的影響. 例如， 鋰離子電池充電過程中，在電池正負極施加足夠大的電流， 若鋰離子在電池內部的擴散速度不夠快， 就會出現濃度梯度， 可能會導致電極材料晶體結構內鋰離子的重組， 進而引起相分離. 電化學儲能系統中通過描述離子輸運特性刻畫微觀物理圖像至關重要. 實驗研究發現鋰在FePO4晶體中的擴散具有很強的各向異性，LixFePO4具有分離成富鋰相和貧鋰相的強烈傾向.LixFePO4完美晶體中的Li 輸運局限于y方向的一維通道， 橫向擴散的可能性很小(圖4(a))， 這一觀點也從相場角度得到了驗證[40-43]. Hong 等[44]運用相場模型為鋰離子擴散各向異性和相邊界遷移機制提供了重要的理解(圖4(b)). Chueh 等[45]通過相場模擬研究了LixFePO4納米顆粒的相干非平衡亞表面相形態. Fleck 等[46]發展了一個考慮各向異性(正交)和非均勻彈性效應的連續相場模型，并模擬了FePO4納米粒子中嵌入Li 時的FePO4相和LiFePO4相之間的轉變過程. 目前， 通過相場模擬方法可較清晰刻畫電化學儲能材料中的離子輸運物理圖像.

雖然已經有大量的相場研究工作為離子輸運行為的實驗現象提供了理論解釋， 但仍有很多問題需要深入研究. 例如， 電池極片的電化學分布特性和充放電過程的相演化規律， 正極材料的相變熱力學特性， 帶電晶格缺陷對電子和空穴濃度以及局部自由電荷的影響等. 第一性原理計算、分子動力學、相場模擬、有限元分析和機器學習等多種尺度的計算方法都可以用于描述電池材料離子輸運過程中的關鍵科學問題[6]， 如何將相場模擬與其他計算方法相結合， 通過多尺度探究離子輸運特性等物理圖像來指導電池的設計， 也是未來需要研究的問題.

3.2.2 電極材料中的力學行為

金屬陽離子嵌入和脫出電極的過程， 會導致電極晶體結構膨脹和收縮從而產生應力[47，48]. 陽離子在固態電極中的擴散會使電極成分偏離其化學計量狀態， 同樣會導致體積變化并產生應力[47，49]. 應力的產生通常會造成電極的彈性和塑性變形(圖5)[50].Chen 等[51]將相場模型與彈塑性變形相結合以研究硅電極嵌鋰過程中內部的相、形貌和應力的變化. 該模型中引入總變形梯度乘法分解F=FeFpFs，其中Fe，Fp和Fs分別是彈性、塑性和鋰離子的嵌入/脫出對變形梯度的貢獻. 可以看出， 總變形可以看作是一個非彈性變形和一個彈性變形的累積[52]，這一理論適用于需要考慮間隙原子擴散和彈塑性變形耦合效應的情況. 隨后， Zhao 等[53，54]和Bower等[55]設計了模擬擴散誘導塑性變形的計算框架.Walk 等[56]分別采用小變形和大變形耦合Cahn-Hilliard 方程分析應力演化. Gao 和Hong[50]進一步發展了彈塑性相場模型， 該模型將體積和偏非彈性變形(deviatoric inelastic deformation)都視為鋰化的直接結果.

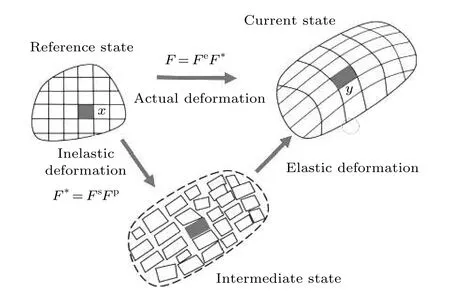
圖5 硅顆粒的彈性和塑性變形[50-52]Fig. 5. Elastic and plastic deformations of Si particles[50-52].

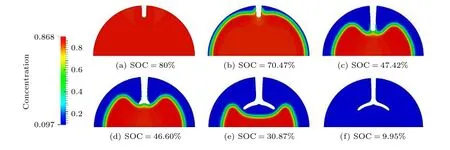
圖6 鋰化過程中的裂紋擴展 (a)初始狀態； (b)相偏析導致裂紋擴展； (c)相界面趕上裂紋尖端； (d)裂紋尖端在相界面處開始分叉； (e)相界面離開裂紋尖端向中心移動； (f)反應停止[73]Fig. 6. Crack propagation during lithiation process： (a) Initial state； (b) phase segregation generates crack propagation； (c) the phase interface catches up with the crack tip； (d) the crack tip starts to branch at the phase interphase； (e) phase interface leaves crack tip and moves towards center； (f) the reaction stops [73].

當金屬陽離子嵌入和脫出電極材料過程中產生的應力較大時， 可能導致電極材料產生微裂紋，理解裂紋擴展的機理對評價與改善電極的可靠性至關重要[48]. 2009 年， Hakim 和Karma[26]以及Aranson 等[57]發展了一個研究裂紋擴展的相場模型. 之后， Marconi 和Jagla[58]， Spatschek 等[59]和Miehe 等[60-62]利用該模型進行了大量的研究.Bhandakkar 等建立了裂紋擴展的內聚模型， 探討了裂紋擴展的臨界特征維數[63，64]. Woodford 等[65]，Zhu 等[66]， Gao 和Zhou[67]以及Klinsmann[68]等分別利用改進的相場模型研究了擴散誘導應力、鋰誘導軟化、實際的電化學加載條件和慣性對鋰電池斷裂的影響等. Zhao 等[54，69]和Zuo 與Zhao[48]利用相場模型研究了Si 粒子中裂紋的萌生條件和裂紋擴展過程. Huttin 和Kamlah[70]以及Liang 和Chen[71]分別研究了LixMn2O4和LiFePO4顆粒的應力產生和裂紋演化. Miehe 等[72]和Zhao 等[73]采用相場模型研究了化學反應對斷口表面組分與微結構的影響 (圖6)， 發現最初的Li 分布濃度是均勻的， 外層失去Li 后出現兩相分布和相偏析， 從而導致了裂紋的擴展.

目前， 通過相場模型對電極材料力學行為的研究較為廣泛， 并成功地解釋了幾個關鍵的實驗觀察結果， 這為設計穩定的鋰電池電極提供了理論指導. 然而， 實際電極材料的內部結構往往非常復雜，仍需進一步研究電極材料中力學行為的決定因素，以及電極中應力改變對電極性能的影響等. 后續的研究還需考慮鋰離子的插層速率、電極顆粒的幾何形狀、電極中的粘彈性力學行為以及微觀尺度上的位錯系統等因素對電極彈塑性變形的影響. 例如，Zhang 等[74]通過第一性原理計算與力學-電化學耦合方程相結合的方法探討了鋰在銅、鋁等集流體中的擴散機理， 結果表明鋰能在具有一定量空位的集流體中以單空位機制擴散， 擴散帶來的體積膨脹可以顯著促進離子在“無負極”電池材料中的擴散， 這也是將來相場模擬需要考慮的問題之一. 鋰離子電池電極的斷裂會破壞電極結構的完整性， 進而對電池安全性及電化學性能造成嚴重的影響. Lu 等[75]綜述了電極斷裂的三種典型類型： 活性層斷裂、界面脫層和金屬箔斷裂， 并揭示了復合電極和薄膜電極中的不同斷裂現象及其相應的機理. 文中提到，目前關于電極斷裂的研究主要是基于實驗觀察與典型機械損傷理論模型， 有關電化學性能和電極斷裂之間的關系的定量研究還很缺乏. 為了推進力學與電化學交叉學科的發展， 從多尺度、多物理的角度認識斷裂是十分必要的. 此外， 對于有裂紋的電極， 裂紋擴展后暴露出新的表面， 并在與電解液接觸的區域發生電化學反應， 導致富鋰相成核. 裂紋尖端附近的應力更容易引起電極變形， 這種變形對成核的影響還需要進一步研究. 為了加快電池材料的設計和優化， 往往需要結合DFT， MD， MC 以及相場模擬等方法進行多尺度模擬， 以獲得對材料體系的整體性理解. Hong 和Viswanathan[76]總結了目前具有相場模擬功能的開源軟件包， 強調了建立完全開源的多尺度模擬框架的重要性， 并提出了“完全開源多尺度仿真框架”的概念.

3.2.3 枝晶生長

鋰枝晶的形成是鋰離子電池廣泛應用的主要障礙之一， 它會導致可逆容量的降低和內部短路[76].因此， 了解這種復雜的非平衡體系的基本物理機制對于提高鋰離子電池的性能至關重要. 在過去的十幾年里， 研究者們從熱力學、動力學和電化學結合的角度出發， 提出了幾種相場模型來理解鋰的沉積和溶解行為[77-82].

2003 年， Monroe 和Newman[83]首次建立了電化學枝晶生長模型， 該模型是鋰聚合物電池中鋰枝晶尖端高度和生長速度演化的綜合數學模型.2004 年， Guyer 等[37，38]建立了一維相場模型， 研究了電沉積過程中的界面電荷分離和動力學行為. 隨后Shibuta 等[84]將Cahn-Hilliard 方程與Butler-Volmer 方程耦合， 模擬二維電沉積過程. 圍繞電極反應過程中電極/電解質界面動力學與界面形貌展開研究， 并考察了界面形貌與外加電壓和反應系數的關系， 證實了超電勢是影響電沉積速率的因素，并發現電沉積尖端半徑與枝晶生長速度的平方根成反比， 這與凝固過程中的枝晶生長理論一致[85].然而， 以上模型都以線性電化學反應動力學為基礎， 當體系遠離平衡時， 該反應動力學將不再適用.針對這一情況， Miehe 等[72]和Liang 等[86]提出了一個非線性相場模型， 該模型考慮了Butler-Volmer反應動力學， 可以在不考慮SEI 層效應的情況下模擬和預測鋰離子電池充電過程中的鋰沉積行為. 在此基礎上， Chen 等[87]建立了熱力學一致的相場模型來研究鋰枝晶結構， 圖7 為序參量、Li+濃度和電勢分布的演變. 在充電過程中， 相場的演化與鋰離子濃度和電勢有關， 這是由于電極和/或鍍層附近存在濃度梯度和電位梯度. 由于尖端效應， 沉積鋰的尖端有較大的Li+濃度和電勢梯度， 從而產生較大的過電位加速其生長最終形成枝晶結構.

Tan 等[88]采用拉格朗日描述法對各向異性電解質溶液中的枝晶生長模型進行了改進. Yurkiv等[89，90]改進了Tan 等的模型以研究應力和SEI 對鋰電沉積的影響， 重現了實驗中經常觀察到的Li 的絲狀結構. Yan 等[91]通過相場方法研究了熱效應對鋰枝晶生長的影響， 并定義了垂直和水平方向的枝晶長度比用以描述枝晶形貌的變化. Hong和Viswanathan[92，93]在開源軟件MOOSE上建立了一個基于大電位的非線性相場模型， 揭示了枝晶生長與離子輸運和電化學反應之間的密切競爭關系， 定義出“各向異性生長因子”(AGF)來量化尖端和谷底區域界面生長的不均勻性. 為研究電池自生熱抑制枝晶的現象， Hong 和Viswanathan[94]結合能量平衡方程提出了一個完全熱耦合的相場模型. 將離子輸運和電化學反應速率之間的相互作用視為溫度的函數， 探索了利用自生熱誘導抑制樹枝晶的可能性. 研究發現， 根據電化學反應勢壘和離子擴散勢壘的不同， 自加熱可以加速(較大的反應勢壘)或減慢(較大的擴散勢壘)枝晶的形成. Jana等[79]使用相場方法評估了電流密度對鋰枝晶生長的影響， 研究表明， 在低電流密度下， 鋰枝晶生長的驅動力來源于尖端控制， 但形態通過塑性流動形成， 使得金屬鋰表面生長較平整. 在高電流密度下，由于彈性能的局域性， 電沉積速率主導應力弛豫動力學， 有利于枝晶的分支. 對于非常高的電流密度，質量快速積聚導致尖端應力弛豫很慢， 因此仍局限于在低級的分支. 由于尖端處應力局域化與濃度梯度的作用， 形成了樹枝狀形貌. 這種非均相電沉積形成小的表面擾動， 形成了細長并高度分支的鋰枝晶. Mu 等[95]通過相場模擬發現致密的SEI 結構可以更好地抑制鋰枝晶的生長. Zhang 等[96]采用相場模型描述了不同導電結構的Li 枝晶生長， 發現枝晶的形態與不同的電子導電結構有關.

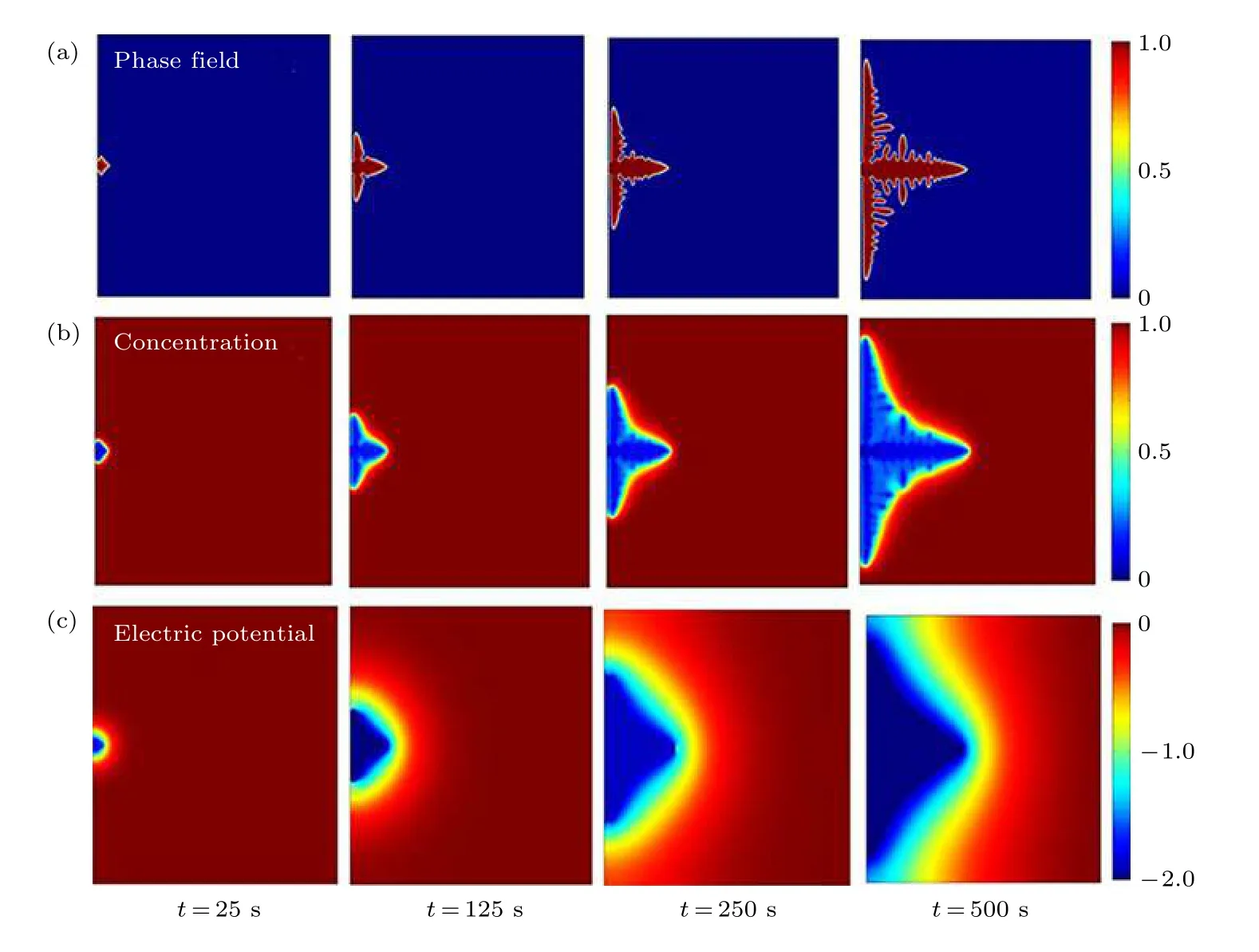
圖7 相場模型模擬的Li 枝晶生長 (a) 序參量， (b) Li+濃度和(c)電勢的演化[87]Fig. 7. Dendrite growth of Li simulated by phase-field model： evolution of (a) order parameter， (b) concentration of Li+， and(c) electric potential [87].

針對鋰離子電池中的枝晶生長， 已有大量的相場模擬研究， 但是需要進一步解決不少問題， 如模型中缺乏熱力學數據庫的耦合， 導致模擬結果與實驗結果無法較好的吻合， 相場模擬只能粗略地重現和解釋實驗現象， 而難以準確預判或改善材料性能. 在目前研究固態電解質對枝晶生長影響的相場模擬中， 電子傳導的影響還未考慮. 電解液中的添加劑可有效地抑制枝晶生長， 但是具體的抑制機制還需深入的探究. 雜合離子電解質對枝晶生長的抑制機制還未在相場模型中進行研究. 電流密度對枝晶的形成有顯著影響， 但其內在控制機理還有待進一步探究. 另外， 金屬負極電極反應的本質是沉積-溶解機制， 然而目前相場模擬關于枝晶的研究主要集中于沉積過程， 而溶解過程很少考慮.

4 總結與展望

4.1 理想的新相場模型及其應有的性質

目前電化學儲能材料的相場模擬已從二相系邁向多相系， 從二元系邁向多元系， 從無外場體系邁向一個或多個外場的體系， 其微結構演化模擬需要一個適用于多元多相系的更嚴謹更自洽的相場模型. 理想的多元多相系的新相場模型應具以下性質：

1) 場變量的演化方程在時間和空間上連續.在此情況下， 相數、組分數等不連續量不能在演化方程中出現. 如果模型給出相濃度方程， 則在相界面過渡到體相時， 它應該自然退化為Fick 擴散方程.

2) 場變量的演化方程直接反映其滿足的約束條件， 選擇不同的獨立變量將給出相同的模擬結果. 因此， 相場方程需要與相容， 相濃度方程需要與為α相中i組分的摩爾分數)相容.

3) 場變量的演化方程可自動確保其在恰當的區間范圍， 模擬中除了數值誤差外， 盡量避免截斷處理.

4) 在數值模擬中， 應嚴格按照演化方程和能量泛函來計算場變量， 剔除為了使得模擬結果與物理事實相一致而運用的非邏輯性數學處理方式. 例如， 為了控制界面散開而引入的平均界面驅動力；為了控制界面移動速度而引入的截斷驅動力.

5) 場變量的演化方程與近距作用觀點相一致.因此， 如果β相逐漸消失， 則它對α相演化的貢獻要逐漸變為0； 如果j組分逐漸消失， 則它對i組分的擴散通量貢獻也要逐漸變為0.

6) 相場方程全域而非局域描述相的演化， 無需任何關于模擬區域的判斷準則. 在這種情況下，不論是在有α相的區域還是在無α相的區域， 實際模擬中的φα都可以通過在整個模擬區域求解其演化方程而得到.

4.2 相場模型在電化學儲能材料領域的應用展望

目前， 可充電電池中大多數的相場模擬仍然處于定性、半定量和定量研究混合的層次. 可充電電池相場模擬向定量化發展需要體系的精確熱力學和動力學數據庫. 畢竟， 相場模型的有效性和合理性在很大程度上依賴于體系的物理、化學和力學參數以及準確的熱力學和動力學數據庫. 此外， 實際的可充電電池是十分復雜的體系， 電池中發生的物理過程跨越多個空間和時間尺度， 這使得電池的直接建模非常困難， 目前仍然缺乏將不同尺度的建模工作進行整合的統一多尺度計算模型. 因此， 進一步的相場模型需要結合DFT， MD 等計算方法發展成多尺度模型， 消除可調參數， 通過理論計算或實驗測量得到模擬中的所有參數.