動態異面壓縮下鋁蜂窩平均坍塌應力分析與試驗驗證
朱宇博,榮吉利,宋乾強,張 濤,吳志培
(1.北京理工大學宇航學院,北京 100081;2.北京宇航系統工程研究所,北京 100076;3.中國運載火箭技術研究院,北京 100076)
0 引 言
鋁蜂窩材料具有相對密度低、質量輕、比剛度比強度高、緩沖吸能性能好、耐腐蝕耐老化、制造工藝成熟等特點[1-3],常作為一種緩沖器材及防撞結構應用在航天器上吸收著陸沖擊能量[4-7]。鋁蜂窩優越的緩沖性能主要歸功于其良好的異面壓縮性能。
如圖1所示,當沿著z軸方向壓縮鋁蜂窩時,稱之為異面壓縮;而在xy平面內壓縮鋁蜂窩時,稱之為面內壓縮。
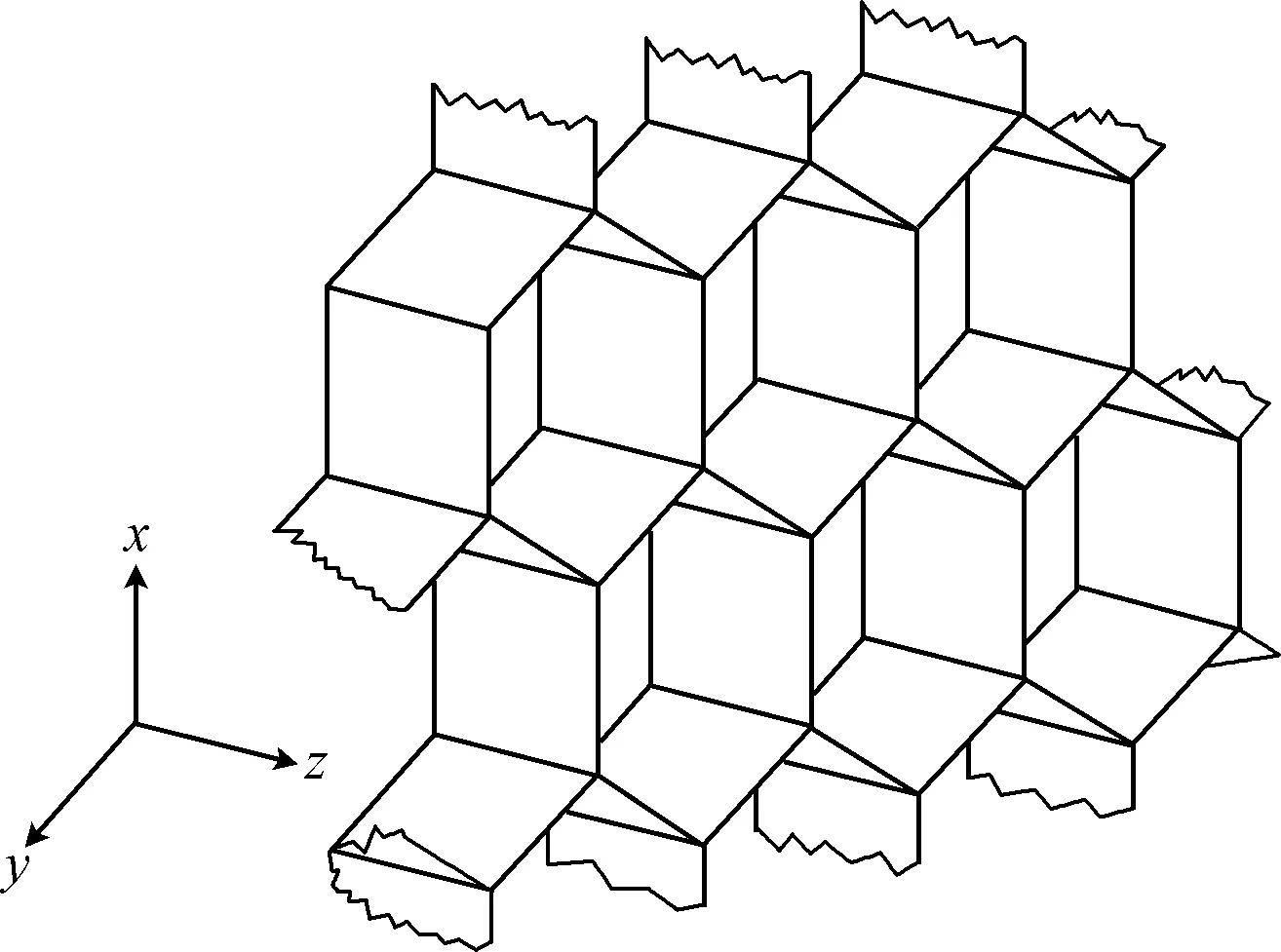
圖1 鋁蜂窩異面示意圖
在鋁蜂窩異面壓縮的理論研究方面,Wierzbicki[8]于1983年給出了單雙壁規則(鋁蜂窩單元的六個面中有四個面具有單倍壁厚、兩個面具有雙倍壁厚),并提出了“超折疊單元理論”。Gibson等[9]在Wierzbicki的研究基礎上,通過對六邊形鋁蜂窩的理論及試驗研究后給出了六邊形鋁蜂窩受準靜態異面壓縮時的平均塑性坍塌應力計算公式
(1)
式中:σ0為鋁蜂窩的屈服應力,t為鋁蜂窩壁厚,l為鋁蜂窩邊長。式(1)為鋁蜂窩異面壓縮中平均塑性坍塌應力的經典計算公式,但是由于簡化假設,使得理論應力值與實際應力值之間常常存在較大偏差(超過15%)。
榮吉利等[10]簡化了超折疊單元理論,給出了兩個準靜態異面壓縮下鋁蜂窩平均塑性坍塌應力的理論計算公式,理論計算應力值與試驗應力值相比誤差較小(小于10%)。不過,由于在動態沖擊中,材料具有應變率效應,榮吉利等的研究不適用于動態沖擊工況。
而在鋁蜂窩吸能裝置的使用過程中,通常承受的是動態沖擊載荷,所以研究動態沖擊載荷下鋁蜂窩的平均塑性坍塌應力具有很高的工程意義。羅昌杰等[11]基于蜂窩材料的對稱性特點,根據能量守恒原理,推導了動態壓縮下鋁蜂窩的平均坍塌應力,不過與試驗應力相對比,誤差在-6.08%~12.04%之間,精度并不高。
本文在榮吉利等[10]研究的基礎上,考慮鋁蜂窩材料應變率效應對力學性能的影響,根據Cowper-Symonds模型,求取了應變率的表達式,推導了鋁蜂窩動態平均塑性坍塌應力計算公式,并通過落錘沖擊試驗及仿真計算,驗證了理論推導的正確性與有效性,本文提出的理論公式較前人研究成果具有更高的計算精度。
1 鋁蜂窩異面壓縮理論推導
鋁蜂窩受異面載荷作用下典型的應力-應變曲線如圖2所示,鋁蜂窩變形依次經過彈性變形段、坍塌平臺段以及密實段。鋁蜂窩在坍塌平臺段應變不斷增加,而應力基本保持不變,形成平臺應力,是能量吸收的主要部分,也是研究的重點,此階段的平均應力就稱為鋁蜂窩的平均塑性坍塌應力[10]。

圖2 鋁蜂窩典型應力-應變曲線
1.1 準靜態壓縮下鋁蜂窩平均塑性坍塌應力推導
圖3所示為鋁蜂窩基本折疊單元示意圖。鋁蜂窩在壓縮過程中會形成重復性的折疊單元,一個基本折疊單元長度為2H(稱為折疊波長),一般以基本折疊單元為研究對象分析鋁蜂窩的異面壓縮性能。

圖3 鋁蜂窩基本折疊單元示意圖
榮吉利等[10]以如圖4所示的六邊形鋁蜂窩單元為研究對象,此單元包括4個雙倍壁厚的面和8個單倍壁厚的面。

圖4 單個完整鋁蜂窩單元
根據能量守恒定律及能量最低原理,得到了Tresca屈服準則下的準靜態平均塑性坍塌應力
(2)
以及Mises屈服準則下的準靜態平均塑性坍塌應力
(3)
該模型只體現了鋁蜂窩結構平均塑性坍塌應力與鋁蜂窩材料屈服應力、鋁蜂窩結構的胞壁厚度t和胞元邊長l間的關系,只適用于準靜態壓縮工況,沒有考慮動態壓縮工況中材料應變率效應對鋁蜂窩結構坍塌變形的影響。
1.2 動態壓縮下鋁蜂窩平均塑性坍塌應力推導
根據Cowper-Symonds模型[12-14],考慮鋁蜂窩材料應變率效應對力學性能的影響,其動態平均塑性坍塌應力
(4)
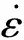
為了計算鋁蜂窩單元的應變率,將一個正六邊形單元等效為半徑為R的薄壁圓筒來處理[11]。鋁蜂窩的六邊形單元(不含支線)包含2個雙倍壁厚的面和4個單倍壁厚的面,所以根據周長相等原則,有
2πR=4l+2×2l=8l
(5)
可以求得等效圓的半徑
(6)
基本折疊單元如圖5所示。
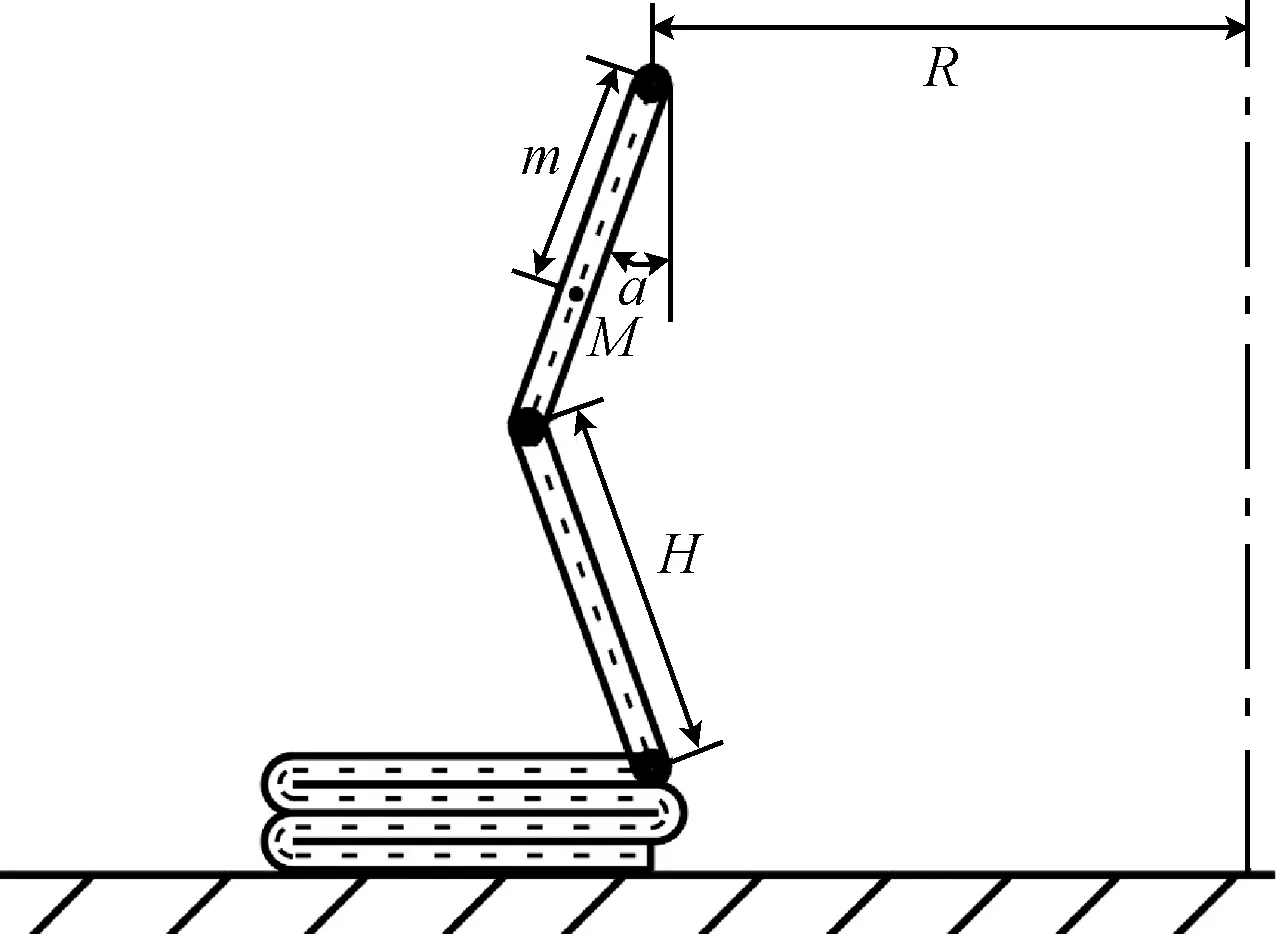
圖5 基本折疊單元
基本折疊單元上任意一點M(距離塑性鉸距離為m)的應變為
(7)
一個基本折疊單元折疊完成后,α=π/2,所以,折疊單元的平均應變
(8)
由此可求得應變率
(9)
式中:T為壓縮時間,vm為平均壓縮速度,H為折疊半波長。
對于落錘沖擊加載,初速為v0,由于壓縮時間很短,可近似認為vm=v0/2,由此可得應變率
(10)
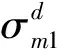
(11)
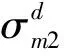
(12)
2 鋁蜂窩異面壓縮試驗驗證
2.1 鋁蜂窩試驗件相關參數
為了驗證以上理論推導的正確性,本文以5052鋁蜂窩為試驗對象,做了若干準靜態及動態壓縮試驗。5052鋁蜂窩的材料參數如表1所示。

表1 5052鋁蜂窩材料參數
5052鋁蜂窩的物理參數如表2所示。

表2 5052鋁蜂窩物理參數
正六邊形鋁蜂窩在加工成所需形狀時,其橫截面中每個六邊形單元很難精確切割成完整的單元,針對圖6中的鋁蜂窩結構常采用圖中虛線所示的分割方法將其分割成Y型單元來計算其橫截面面積。
圖6中Y型單元的面積SY
(13)
正六邊形鋁蜂窩在切割成正六邊形形狀時,其Y型單元的個數NY
NY=6n2+12n+6
(14)
式中:n=(N-1)/2,N為正六邊形形狀鋁蜂窩最長邊上完整的六邊形單元個數(由于鋁蜂窩切割成正六邊形形狀,故N為奇數,圖6中N=3)。

圖6 六邊形鋁蜂窩結構Y型單元劃分
結合式(13)和式(14)可得正六邊形鋁蜂窩結構橫截面積S,
(15)
本文采用的5052鋁蜂窩試件,N=11,S= 4489.476 mm2。
2.2 鋁蜂窩的準靜態壓縮試驗
對鋁蜂窩試件進行了3次準靜態壓縮,得到的力與位移曲線如圖7所示,其中力是鋁蜂窩受試驗機壓縮的力,位移是鋁蜂窩頂端的位移也是鋁蜂窩的壓縮變形量。試驗中壓縮速度為2 mm/min。從圖7可以看出,鋁蜂窩在準靜態壓縮下力-位移曲線具有很好的一致性,塑性坍塌力約為3919 N。
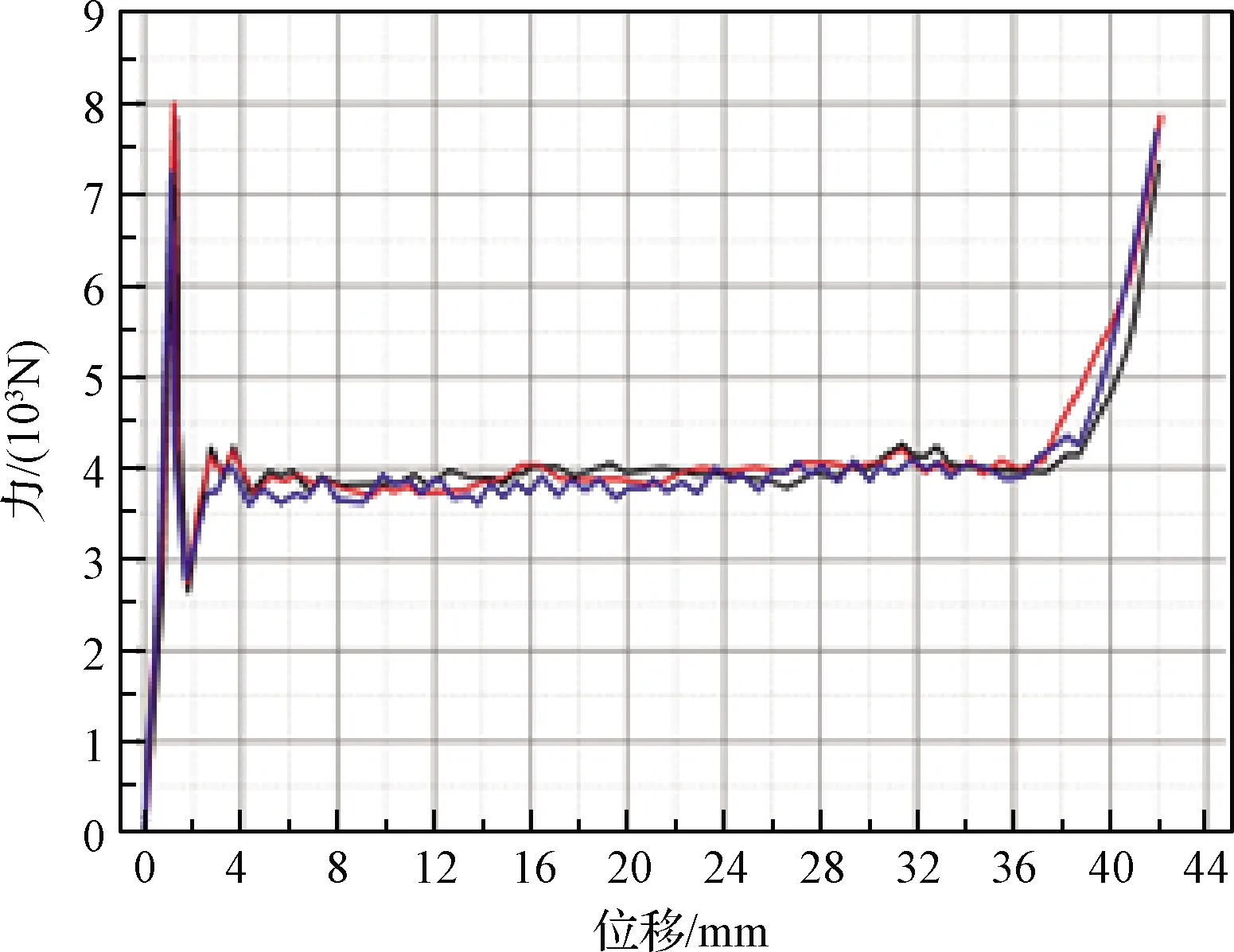
圖7 5052鋁蜂窩準靜態壓縮力-位移試驗曲線
鋁蜂窩的平均塑性坍塌應力的試驗結果及理論值如表3所示,從表3可以看出:經典的半經驗公式即式(1)相對于試驗值偏小,誤差為17.068%;式(3)的計算結果相對于試驗值偏大,誤差為-6.529%;式(2)的計算結果與試驗結果高度吻合,誤差僅為0.916%。

表3 5052鋁蜂窩準靜態壓縮試驗結果與理論計算對比
2.3 鋁蜂窩動態異面壓縮試驗研究
2.3.1試驗工裝
采用WANCE落錘沖擊試驗機測量鋁蜂窩動態壓縮性能,試驗工裝如圖8所示。

圖8 鋁蜂窩動態壓縮試驗工裝
在中質錘體下落壓縮鋁蜂窩前一刻通過速度傳感器測量中質錘體的壓縮速度,試驗的反作用力通過中質錘體中的力值傳感器進行測量。為了防止損壞力值傳感器,在中質錘體下面安裝了緩沖器,中質錘體從一開始接觸鋁蜂窩到與緩沖器接觸整個過程行程約為24 mm(即鋁蜂窩的有效壓縮長度)。
2.3.2動態壓縮試驗結果
對鋁蜂窩試件進行了如表4所示的6種不同工況下的試驗,試驗中設定了錘體不同的壓縮能量,并在試驗中用測速傳感器對錘體壓縮鋁蜂窩前一刻的壓縮速度進行精確測量,不同工況下的壓縮速度測量結果如表4所示。

表4 動態壓縮試驗工況
6種工況下5052鋁蜂窩動態壓縮力-位移曲線如圖9所示。在工況1中,由于壓縮能量較小,中質錘體沒有與緩沖器接觸,鋁蜂窩并未到達密實階段。在工況2~6中,由于壓縮能量較大,中質錘體從剛接觸鋁蜂窩開始運動24 mm后即與緩沖器相接觸,其后的測量值并不準確,即工況2~6中力-位移曲線在24 mm內有效。錘體與緩沖器接觸后,部分力被緩沖器吸收,越往后壓縮緩沖器吸收的能量越大,作用在鋁蜂窩上的力越小,直到為零,故導致工況2~6中力-位移曲線在24 mm以后力值逐漸減小。

圖9 鋁蜂窩動態壓縮力-位移試驗曲線
3 鋁蜂窩動態壓縮的有限元仿真校驗
3.1 有限元模型的建立
有限元仿真采用ANSYS/DYNA軟件,使用全尺寸有限元模型對鋁蜂窩試件進行有限元分析。如圖10所示,鋁蜂窩自由放置在剛性面上,上剛性面質量為中質錘體總質量8.8 kg,并施加不同工況下對應的初始速度。鋁蜂窩采用Belytschko-Tsay型殼單元,材料模型采用與應變率相關的隨動塑性材料模型,鋁蜂窩之間采用單面接觸,鋁蜂窩的材料參數見表1及表2。

圖10 鋁蜂窩有限元模型
3.2 仿真計算結果
在工況1的壓縮速度下,鋁蜂窩在變形過程中的應力變化情況如圖11所示。從圖11(b)~(f)可以看出:鋁蜂窩在壓縮過程中頂部的應力值最大,底端其次,中間最小。鋁蜂窩在很短的時間內(約0.05 ms),上部應力達到最大值,此值對應鋁蜂窩彈性變形階段的峰值壓力。在隨后的壓縮過程中鋁蜂窩頂部、中部以及底部的應力值均減小并趨于平穩,圖11(c)~(f)中上部的最大應力值對應鋁蜂窩的塑性坍塌應力。鋁蜂窩中部除了在其剛受到壓縮的很短時間內應力較大外,其余時間均較小。圖11中鋁蜂窩的應力分布及變化情況與實際壓縮過程中鋁蜂窩的變形過程吻合。

圖11 鋁蜂窩變形過程
圖12為鋁蜂窩在工況1~工況6下的力-位移仿真曲線。值得說明的是在計算工況1和工況2時,由于初始速度較小,鋁蜂窩壓縮的時間較長,為了節約計算資源,并未計算鋁蜂窩的整個壓縮過程。
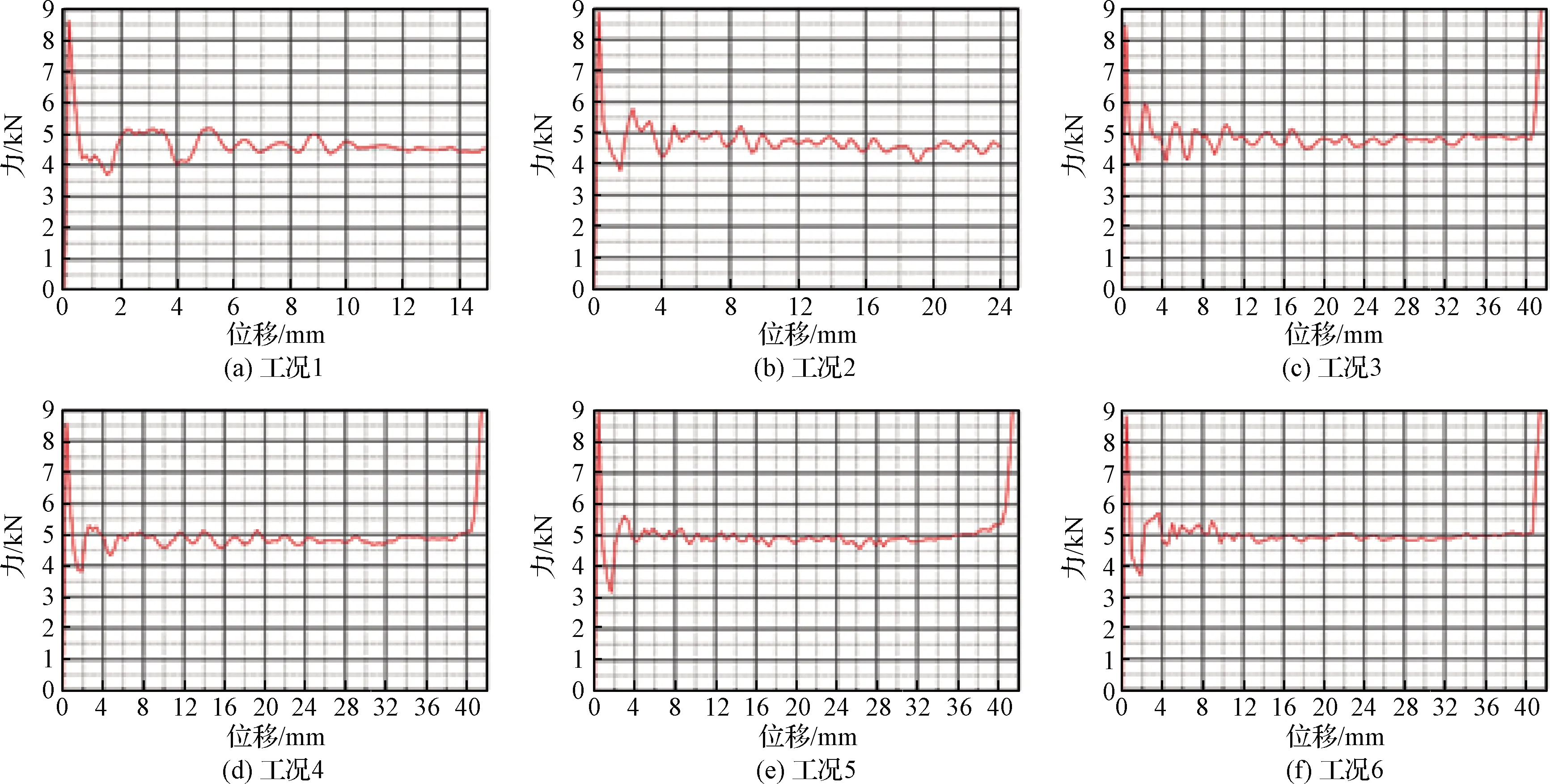
圖12 鋁蜂窩動態壓縮力-位移仿真曲線
4 理論、試驗及仿真結果討論


表5 各工況下試驗應力、計算應力、仿真應力對比
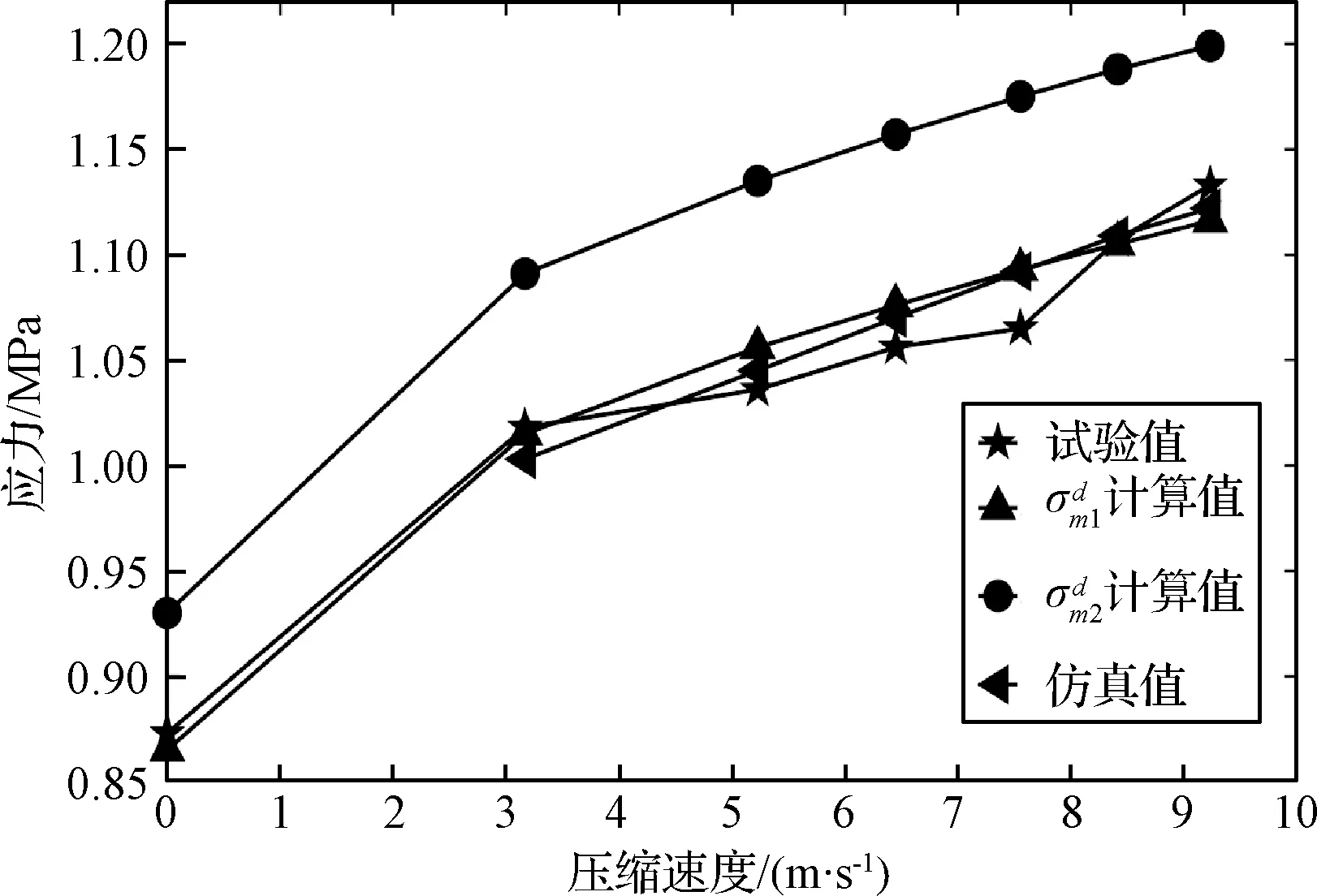
圖13 動態壓縮下鋁蜂窩應力-壓縮速度曲線
5 結 論

本文所做工作可對動態壓縮下鋁蜂窩的異面壓縮性能研究提供一定的工程借鑒,以便為鋁蜂窩吸能裝置的設計提供理論指導。

