離心泵負載下的電機定子電流特性研究*

龔 波， 袁壽其， 駱 寅， 韓岳江， 董 健

(江蘇大學國家水泵及系統工程技術研究中心 鎮江,212013)

引 言

離心泵被廣泛應用于生產和生活中，監測離心泵運行狀態，保證離心泵的安全可靠運行一直是眾多學者研究的焦點。陳長盛等[1]研究了利用了振動信號來監測離心泵運行狀態。Pavesi等[2]利用壓力脈動信號來監測離心泵內部不穩定流動。這些方法使用的傳感器普遍成本高、安裝難度大；使用的數據采集、傳輸、分析系統一般較復雜，信號采集容易受到干擾，結構可靠性較低[3]。

基于電機定子電流的監測技術興起于20世紀70年代，其原理是將感應電動機作為轉矩傳感器，通過監測電機定子電流信號來監測電機負載的運行狀態。國內多用此技術來診斷電機本體的機械部件的故障，而鮮有將其運用于離心泵狀態監測上。

由電機驅動的離心泵在運行過程中，葉輪葉片會受到輸送介質的反作用力[4]，形成水力負載轉矩。水力負載轉矩在軸上傳遞，最終傳遞到電機轉子軸端，并在電機的定子電流上形成響應，因此監測和分析電機定子電流即可實現離心泵的狀態監測。Siegler等[5]就將這種監測方法應用于海水淡化泵葉輪腐蝕程度的監測上，其準確率高達90%。此后，美國橡樹嶺國家實驗室(oak ridge national laboratory，簡稱ORNL)對此方法進行了深入研究，ORNL主要是利用電機定子電流監測法診斷泵部件的結構故障。Casada[6]研究了離心泵各工況下轉子不對中時的定子電流和瞬時功率的時頻特征。Ahonen等[7-8]建立了一種通過變頻器來實現離心泵運行工況監測的方法，通過從變頻器中讀出當前電流值和電機的轉速，根據已知的泵特性，計算出當前泵的運行工況。

相比于振動信號監測法[9]和壓力脈動監測法等，利用電機定子電流信號分析(motor current signature analysis，簡稱MCSA)方法監測離心泵運行狀態具有以下優點：①非接觸式測量,無需直接在監測設備上安裝傳感器；②采集的信息集成度高，電機及其負載的幾乎全部信息都通過電機定、轉子繞組間的氣隙磁場變化反映在定子電流中；③能用于振動噪聲分析法等不能應用的場合，如潛水泵等[10]。

在離心泵與電機組成的系統中，當前關于定子電流的研究工作集中于故障特征頻率的提取和故障信號能量變化的計算[11]，卻很少有關于離心泵運行在多工況下電機定子電流信號特征的研究。文中以IS-65-50-160型單級單吸離心泵和Y160M-2 B3型電機組成的系統為對象，研究離心泵不同工況下的電機定子電流特性，從定子電流中提取與離心泵運行相關的信息，為實現用定子電流監測離心泵運行和分析離心泵內部流動狀態提供參考。

1 數值模擬與理論分析

在水泵中，轉子軸系上的葉輪葉片會受到輸送流體介質的反作用力，產生反向扭轉力矩。泵在不同工況、流態下運行會產生不同的扭轉力矩[12-14]。扭轉力矩經過轉子軸系傳遞后會在電機轉子上產生扭轉響應，電機的轉子與定子之間存在磁耦合現象，可以通過提取、分析電機定子電流來分析離心泵運行工況。如圖1所示，若能獲得不同流態下水力負載轉矩特征及其經過泵轉子軸系傳遞后的在電機定子電流中響應特性，就可依據電機輸出信號實現流態診斷。因此基于計算流體動力學(computational fluid dynamics，簡稱CFD)技術模擬了不同工況下的離心泵水力負載轉矩特征，通過理論分析電機定子電流與離心泵負載轉矩的關系，并用試驗提取了離心泵不同運行狀態下電機定子電流的特征。

圖1 基于電機電流信號監測泵狀態原理Fig.1 Condition monitoring principle of pump based on MCSA

1.1 離心泵非定常水力負載矩分析

文中選用IS-65-50-160型單級單吸離心泵的設計參數為：設計流量Qd為50 m3/h，揚程為37 m，轉速為2 900 r/min，比轉速為81.5，葉片數為6。對離心泵進行3維建模，對過流部件進行網格劃分，所有網格均為6面體網格，網格質量均滿足非定常計算要求，并對網格無關性進行了驗證，最終確定全流場網格總數為2 926 876。圖2為離心泵流道網格劃分圖。對全流場進行模擬計算,可獲得離心泵在各個工況點下的水力矩特征。圖3為不同工況下的水力矩時域圖。可見，在不同工況下水力矩均成周期性變化，且水力矩整體值隨流量Q增大而增大。水力矩的脈動分量強度隨運行工況點偏離設計點的距離增大而增大，水力矩脈動分量強度的RMS值如圖4所示。

圖2 離心泵流道網格劃分圖Fig.2 Mesh of model pump flow field

圖3 不同工況下的水力矩時域圖Fig.3 Time domain of hydraulic moment fluctuation under different operating conditions

圖4 不同工況下的離心泵水力矩脈動的RMS值Fig.4 RMS of hydraulic moment under different operating conditions

對水力矩時域信號進行快速傅里葉變換(fast Fourier transform，簡稱FFT)得到水力矩脈動分量的頻譜圖。在水力矩頻譜圖中，葉頻分量f2在水力矩脈動強度變化中居于主導地位，如圖5所示，其中:f2為葉頻;f為頻率變量。

圖5 不同工況下離心泵水力矩脈動分量頻譜圖Fig.5 Frequency domain of hydraulic moment fluctuation under different operating conditions

水力矩經過轉子軸系傳遞后會在離心泵軸端產生對應的扭矩響應，并最終作為負載施加到電機上。通過水-機-電的聯合仿真，即通過Fluent進行水力矩非定常計算，通過Workbench進行軸系扭矩的提取，運用神經網絡進行水力矩到電機負載轉矩的辨識，通過Simulink進行電機建模，并用Fluent中的自定義函數功能(user defined function，簡稱UDF)與Matlab腳本文件的編寫實現Fluent與Simulink的數據傳遞，水力矩與軸端矩在穩態時相等，在瞬態時相關性也極高，總體上可視為相等[15]。湍流、邊界層旋渦脫落等不穩定流動現象及不平衡的旋轉質量等機械因素也會一定程度上造成軸端扭矩的波動，但這些比水力矩脈動作用要小很多。

1.2 交流感應電動機數學模型

交流感應電動機系統數學模型[16]可以表示為

(1)

其中:第1個式子是傳動系統的轉矩平衡方程式，Te,TL，J，pn，ω分別為電磁轉矩、離心泵負載引起的軸端扭矩、機組的轉動慣量、電機極對數及旋轉角速度。

由第1個式子可見，TL存在擾動時會引起ω發生變化。第2個式子為電機電壓平衡方程。式中u,R,i,L分別為電機定子電壓、電阻、電流和電感參數，θ為機械扭轉角。式中的第2項和第3項為電磁感應電動勢，Ldi/dt是由于電流變化引起的感應電動勢，ωidL/dθ為轉子和定子之間的相對位置變化引起的感應電動勢。

由于電網容量較大，u可視為不隨負荷變化。結合轉矩平衡方程可知，當軸端扭矩TL存在擾動時會導致ω變化，會導致i發生變化，i的改變最終會改變Te，從而形成新的轉矩平衡。

可以看出，電流、磁通、扭矩之間的關系較復雜，不能直接由電流的變化情況反映扭矩波動情況。在此采用M-T坐標變換[17]法將問題簡化得到各向電流與產生Te的電流分量isT和產生恒定的有效磁通的勵磁電流分量isM的關系。

(2)

簡化后的電磁扭矩、磁場、電流的關系可用下式表示

(3)

其中:P為電機的結構常數；λs為定子磁通，與電機輸入電壓、電機結構和負載相關，在泵與電機組成的系統中離心泵可視為穩定負載，擾動轉矩對電流的影響很小，所以λs可視為常數。

因此，可認為Te與其電流分量isT線性相關。由此可見，雖然isT不能直接測量，但通過坐標變換，isM，isT與相電流之間有著定量關系，因此電磁轉矩可以間接反映在定子電流中。

假設轉軸扭矩的擾動頻率是f0，則感應電動機的氣隙扭矩T包括平均轉矩T0和軸轉矩波動T1之和

T=T0+T1cos(2πf0t+φ)

(4)

其中：φ為電機轉軸可能產生的扭振相位。

定子電流由isM和isT組成。isM和isT可分解為平均部分和波動部分

Is M=Is M0+As Msin(2πf0t+φM)

(5)

IsT=IsT0+AsTsin(2πf0t+φT)

(6)

因此,各相電流可分解成isM和isT的組成形式，如A相

Is a=Is Msin(2πfet)+IsTcos(2πfet)

(7)

化簡可得

(8)

其中:IsM0=I0cosφ0;IsT0=I0sinφ0;φ0=tan-1(IsT0/IsM0)

由式(8)可看出，扭矩的波動頻率f0會對電網工頻形成調制；定子電流主要由平均電流分量和波動電流分量組成，平均電流對應的頻率為fe，波動電流在f0-fe和f0+fe處會有對應的分量，且f0-fe處的幅值要大于f0+fe處。由前面分析知水力矩與軸端扭矩可認為近似相等，水力矩脈動是造成軸端扭矩波動的最主要原因，因此水力矩脈動的頻率對應的為軸端扭矩的波動頻率f0，以調制的方式反應在定子電流信號中。

其他因素，如湍流、邊界層旋渦脫落等不穩定流動現象以及不平衡的旋轉質量等機械因素，也會一定程度上導致扭矩的波動，但是其影響會遠遠小于水力矩的影響，并最終也反映在定子電流諧波中。

仔蝦期餌料投喂用配合飼料（蝦片）與大鹵蟲輪投，每2～3h一次，并隨時觀察仔蝦胃腸飽滿情況適時加以調整，以滿足仔蝦攝食量的要求。此階段水溫控制在25～26℃，出池前5d逐漸將水溫降至自然溫。日換水量為1/2左右，換水網箱網目為40目。充氣量呈翻騰狀，以防止餌料沉積，敗壞水質。適度保持水中大鹵蟲數量（每升水1～2個），避免仔蝦期出現殘食現象。

2 試驗與數據采集

在江蘇大學國家水泵及系統工程技術研究中心實驗室的閉式試驗臺上對離心泵進行測試。試驗裝置由儲水罐、真空泵、進出水管閥、電機、測試泵、渦輪流量計、壓力傳感器、扭矩儀、軸編碼器、直流穩壓電源等組成。試驗裝置示意圖如圖6所示，裝置現場布置圖如圖7所示。試驗采集的數據有流量、進、出口壓力等，采集頻率為10 kHz。其中渦輪流量計安裝在排出管路上，基本誤差限為；進口閥門為手動式蝶閥，出口閥門為電動閥門，閥門控制器的精度可達0.1%；進出口壓力傳感器均為WIKA S-10型，精度為0.25%，安裝在進口法蘭上游和出口法蘭下游2倍的管徑處；采集的數據通過采集板卡NI-USB6343傳輸到計算機，由計算機完成數據的處理和運行的控制；通過霍爾傳感器測得電機定子電流。

圖6 試驗裝置示意圖Fig.6 Schematic of experimental rig

圖7 試驗臺Fig.7 The test platform

整個測試系統是基于NI公司的虛擬儀器技術，結合了PXI系統和多功能動態數據采集卡組成的硬件測試系統與由LabVIEW開發的軟件系統，最終形成的一套自動采集數據的系統。其測試原理如圖8所示。

圖8 測試原理Fig.8 The principle of test system

通過調節出口電動閥門來改變離心泵運行工況，調節閥門后靜待2 min至工況穩定，開始記錄采集到的數據，采樣頻率為10 kHz，連續采集10 s并保存。再次調節閥門，重復上述操作。直至采集到0.1Qd, 0.2Qd,0.3Qd, 0.4Qd, 0.5Qd, 0.6Qd, 0.7Qd, 0.8Qd, 0.9Qd, 1.0Qd, 1.1Qd, 1.2Qd和1.3Qd工況下的試驗數據，結束試驗。

3 試驗結果與信號預處理

為了使得試驗數據更加可靠，對每個工況點的試驗數據持續采集10 s，取10 s內的平均值，計算得到相關的揚程功率等。根據3次外特性試驗中采集到的數據繪制該泵的外特性曲線，如圖9所示。

圖9 測試泵外特性曲線Fig.9 Performance characteristics of the test pump

從圖9中可以看出,3次試驗曲線基本一致，可見試驗數據可靠性較高。由揚程特性曲線看出，該泵的揚程性能曲線存在著駝峰現象，當流量在0～20 m3/h時，揚程隨流量的增加呈小幅增加趨勢，當流量大于20 m3/h時揚程隨流量增加呈下降趨勢。小流量(0～20 m3/h)下離心泵內部流動不穩定，流動損失較大，此時離心泵內部流體的流動不穩定可能會使得泵產生較大振動，也會造成泵軸上扭矩的波動，產生更多的諧波。由效率曲線可以看出，當離心泵運行在設計工況附近時效率較高，因為當離心泵運行在設計工況附近時流動更穩定，水力損失較小；當離心泵運行偏離設計工況時，因為離心泵偏離設計工況運行時水力損失較大，導致效率降低。

3.1 定子電流信號時域分析

定子電流的時域圖如圖10所示。由圖10可知，定子電流總體上符合正弦交流信號特征,頻率為與電網工頻相同的50 Hz,可見電網工頻信號在定子電流中占據著主導地位，而離心泵負載轉矩波動導致的定子電流波動則較弱。對比標準工況下的電機定子電流信號與電源電流發現，其與電源電流正弦交流信號波形有些許偏差，這種偏差可能與離心泵負載有關。定子電流信號的平均大小隨著離心泵運行工況而改變，可采用RMS來衡量定子電流的平均大小。定子電流的均方根隨流量的變化趨勢如圖11所示。

圖10 設計工況下的定子電流時域信號Fig.10 Stator current time domain signal at the design point

圖11 定子電流和水力矩隨流量變化圖Fig.11 Stator current value and hydraulic torque versus operation point

從圖11中可見，定子電流與離心泵水力矩隨運行工況變化的規律相似，這主要是因為流量的增大流體對葉片的反作用增大導致水力矩增大，水力矩增大使得軸端扭矩增大，電機的輸出功率增大，反應在定子電流中為定子電流的增大。因此，定子電流在一定程度上可作為運行工況監測的參考指標。

3.2 定子電流信號的頻域分析

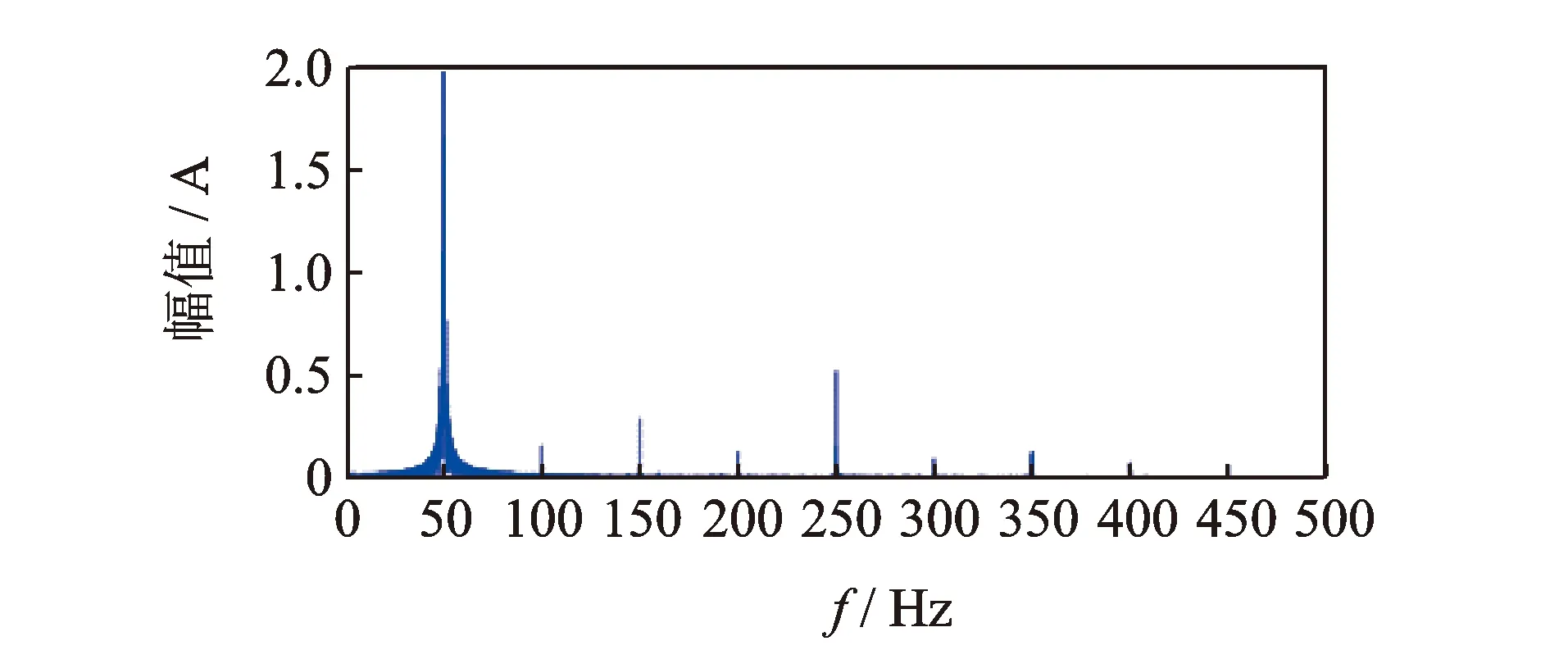
圖12 設計工況下定子電流頻譜圖Fig.12 Frequency characteristic component of the stator current at the design point

3.2.1 定子電流信號的預處理

為了更好地比較不同工況下的定子電流特征，將定子電流按照式(9)作歸一化處理，以便在相同的幅值區間內比較不同工況下的定子電流特征。

I1=(I-Imin)/(Imax-Imin)

(9)

奇異值分解法(singular value decomposition,簡稱SVD)[18]是一種消除電網工頻干擾獲得弱信號的有效方法。SVD是一種起源于線性代數的矩陣分解法，其基本原理在于通過SVD處理后信號中的特征成分被分解到不同的正交子空間，在定子電流中，電網工頻在定子電流信號中占據著主分量地位，因此電網工頻會被分解到第1主分量對應的相空間中，這樣就可以剔除電網工頻對應的電流分量。

奇異值分解法首先需將一組離散的定子電流信號重構成一個N×M的矩陣A，其中M為一個周期的信號長度[19]。

(10)

然后，將矩陣A分解成U,Λ,V相乘的形式[10]

(11)

取U中第1列u1，Λ中第1個元素σ1，V的第1列v1轉置相乘構成矩陣，即為基頻對應的奇異矩陣

(12)

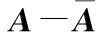
圖13 消除電網工頻后設計流量下定子電流頻譜圖Fig.13 Current spectrum after elimination of power frequency at the design point

對比圖12,13可知，經過SVD處理后，50 Hz軸頻是主要頻率，之前被淹沒在電網電流信息中的與離心泵運行狀況相關的弱信號開始顯現出來，信噪比得以提升。

3.2.2 諧波分析

軸端扭矩的波動會以諧波的形式反映在電機定子電流中[20]。總諧波失真(total harmonic distortion,簡稱THD)是指所有高次諧波幅值均方根與基頻幅值之比。THD反映的是諧波成分的大小,高的諧波失真值意味著高次諧波成分越多，扭矩波動愈強烈，因此計算定子電流的總諧波失真值可用來判斷扭矩波動情況，進而反映泵內的流動狀態的穩定性。

運用LabVIEW程序測得SVD處理后的定子電流，得到處理后的定子電流的總諧波失真。各工況下的總諧波失真值如圖14所示。

圖14 消除電網工頻后不同工況下定子電流THD值Fig.14 THD of the current at the operation point after elimination of power frequency

結合圖4、圖9及圖14分析可知，當離心泵運行在小流量(0～20 m3/h)時，離心泵運行效率低，揚程隨著流量的增加而增加，此時對應的定子電流的THD較大。小流量時離心泵內部流動的不穩定性較強，水力矩脈動也較大，導致了軸端扭矩的波動較為強烈，反映在定子電流中為THD較大，但是小流量時THD隨流量變化不敏感。隨著流量從20 m3/h增加到設計流量附近時，定子電流的THD減小，因為隨著流量的增加水力矩脈動減弱，泵內部流動趨于穩定。當離心泵運行在高效區(45～55 m3/h)，水力矩脈動較弱，泵內部流動較為穩定，定子電流THD較低。可見，定子電流的總諧波失真在一定程度上可以反映離心泵內部流動的穩定性。

4 結束語

基于CFD數值模擬和理論分析了不同工況下離心泵的水力負載轉矩特征及其在電機定子電流上的響應。搭建了試驗臺，借助于霍爾電流傳感器及虛擬儀器技術,測得離心泵在不同運行工況下電機定子電流并對其特征進行了分析。離心泵運行狀態改變會引起水力負載轉矩的變化，最終通過轉子軸系傳遞到電機定子電流中。分析定子電流特征可實現離心泵運行工況的監測。定子電流均方根與離心泵水力矩隨著流量的變化有著相似的變化趨勢，可用定子電流均方根實現工況監測。水力矩脈動的頻率和強度會以信號調制的方式反映在定子電流中。通過SVD分解可實現消除電網工頻提取弱信號的目的。消除電網工頻后的定子電流THD值可為離心泵運行工況和內部流動狀態識別提供參考依據。