凸曲面拼接模具球頭銑刀的瞬時銑削力預測*

吳 石, 張添源, 劉獻禮, 劉海瑞, 楊 琳

(哈爾濱理工大學先進制造智能化技術教育部重點實驗室 哈爾濱, 150080)

引 言

轎車覆蓋件模具具有加工形面曲率變化大、形面復雜、尺寸精度和表面質量要求高的特點，其模具材料大多是為Cr12MoV 和7CrSiMnMoV 等模具鋼[1]。為降低覆蓋件模具整體加工的復雜性，多采用模體和鑲塊式模件拼接結構，整體銑削加工時模具拼接區域存在多種硬度差，鑲塊間硬度差 HRC5-HRC10，鑲塊與模體間硬度差高達 HRC15[2]。在球頭銑刀銑削加工模具拼接區域時，一方面多硬度拼接區的銑削加工易于引發載荷突變，對刀具造成明顯的振動沖擊；另一方面，多硬度拼接區曲面曲率不斷變化，引起未變形切屑厚度、切屑體積隨之變化，導致加工過程中瞬態銑削力變化明顯。這是導致模具加工表面精度下降，表面質量不高的主要原因。因此，研究復雜型面拼接模具球頭銑削的瞬態銑削力具有重要工程意義。

在曲面球頭銑刀瞬態銑削力的研究過程中，Altintas等[3-4]基于微元法將球頭銑刀刃線的空間特征和加工過程時間特征結合起來，引入切削刃微元和瞬時切削寬度求解瞬態銑削力。Zhang等[5]延續了該方法，分析了圓弧角銑削加工過程中銑削力的變化規律。Wei等[6-8]同樣基于時間離散方法研究了自由輪廓曲面和三維曲面加工的瞬態銑削力預測方法。Tuysuz等[9]在考慮球頭銑刀加工變形的情況下修正了三軸銑削和五軸銑削過程的瞬態銑削力，提出了自由曲面球頭刀銑削犁耕力的模型。

在瞬態銑削力預測模型中，切屑厚度是極為重要的時間變量，它聯系著切削加工條件與銑削力微元。Wan等[10]分析了薄壁件銑削加工時切入角對瞬時切屑厚度的影響，提出了未變形切屑厚度的迭代算法。文獻[11-13]提出了基于球頭銑刀刃的二維次擺線軌跡方程的等效切屑厚度，分析了未變形切屑厚度隨著刀具工件接觸區的瞬時徑向切觸角和軸向觸角變化規律。Liang等[14]進一步發展了擺線軌跡方程，建立了三維擺線軌跡方程，基于刀工接觸區邊界建立了球頭銑刀未變形切屑厚度的幾何模型，分析了切屑厚度的時空變化特征。Huang等[15]基于軸向切觸角和刀傾角對切屑厚度進行數值解耦，實現了曲面瞬態銑削力的預測。

在模具曲面加工中，由于形面復雜，刀具與工件的切觸關系沿切削軌跡不斷變化，是曲面加工的最顯著的特點，同時銑削模具不同硬度拼接區域時，瞬時沖擊力對銑削力的影響不能忽視。文中針對凸曲面模具拼接處的瞬時沖擊力，以“弱剛性銑削系統+剛性拼接曲面”加工模式為研究對象，研究瞬時沖擊力及模具曲面曲率變化對未變形切屑厚度時空特征的影響規律，并基于微元法對曲面拼接模具球頭銑刀的瞬時銑削力進行預測。

1 沖擊振動球頭銑刀三維次擺線軌跡

球頭銑刀任意j齒切削刃上的離散點需要經歷四次坐標變換，四次坐標變換矩陣分別為進給矩陣T1-0(fx,fy,fz,t)，旋轉矩陣T2-1(ω,t)，沖擊振動引起的位移矩陣T3-2(Ac)和刀具齒間角矩陣Tj-3(φj)。其中，刀具坐標系O3X3Y3Z3到主軸回旋轉坐標系O2X2Y2Z2的平移變換由于經過模具拼接區域，要考慮沖擊振動引起的位移變化。從j齒切削刃局部坐標系到模具空間坐標系的變換矩陣為

T=T1-0(fx,fy,fz,t)tT2-1(ω,t)T3-2(Ac)Tj-3(φj)

(1)

推導得

(2)

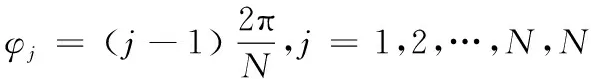
第j齒切削刃參數方程在模具空間坐標系內的表達式為

(3)

第j齒切削刃局部坐標系下的球頭切削刃方程

(4)

其中：R為球頭銑刀半徑;θ(z)為切削刃任意點軸向位置角;μ=(1-cosθ(z))tanβ為切削刃任意點的螺旋滯后角;β為刀具螺旋角。

將式(4)代入式(3)可得球頭銑刀曲面銑削切削刃軌跡方程

(5)

其中:fxt,fyt和fzt為刀具在模具空間坐標系內相對于模具沿O0x0軸、O0y0和O0z0軸方向t時刻內平移距離。

fxt,fyt和fzt可分別表示為

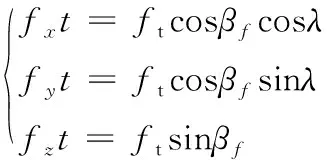
(6)

其中:βf為刀具前傾角;λ為進給方向角。

2 沖擊振動的未變形切屑厚度模型

加工曲面模具過程中，越靠近球頭刀尖時的切削刃實際切削半徑越小，將刀齒運動軌跡近似為圓平移軌跡計算的未變形切屑厚度值，與刀齒運動軌跡為次擺線軌跡計算的未變形切屑厚度值的差越大。為簡化球頭銑刀曲面銑削切削刃軌跡方程，假設進給方向在xOy面投影與x軸重合，即fy=0。在t時間，位置角θ(z)處的切削刃離散微元運動軌跡為

(7)

該運動軌跡即考慮了刀齒三維次擺線運動，又考慮了過模具拼接區域時的沖擊振動，其第j-1齒的刀齒運動軌跡為

(8)

關于曲面銑削第j齒的z向軸向位置角θj(z)與第j-1齒的z向軸向位置角θj-1(z)的關系為

(9)

球頭銑刀的刀齒三維次擺線軌跡如圖1所示，在切削刃θ(zi)位置進行離散，兩齒分別為第j齒和第j-1齒，兩齒在xOy面的軌跡也如圖1所示Oj-1為Oj的前一刀具坐標點。

圖1 兩齒球頭銑刀的三維次擺線軌跡示意圖Fig.1 Schematic diagram of three-dimensional trochoid trajectory of the two teeth ball end cutter

在第j齒和第j-1齒的切削表面分別取切屑厚度控制點Pj-1,Pj,則當t時間第j齒的瞬時未變形切屑厚度為

h(t,θ(z))=|Pj-1Pj|=

(10)

計算瞬時未變形切屑厚度時，需要保證當前刀具中心Oj(xoj,yoj)，與相鄰刀齒的切屑厚度控制點Pj-1,Pj共線，即滿足如下方程

(11)

Pj點、Pj-1點和Oj點在位置角θ(z)的平面運動軌跡，如下式所示

(12)

(13)

(14)

由式(12)得到sinθj(z)，由于球頭銑刀不同位置(zi)的瞬時未變形切屑厚度不同，不同位置(zi)的刀具變形也不同，所以球頭銑刀球頭任意離散位置(zi)的瞬時未變形切屑厚度為

hj(t,θjzi) = (Ri+Lisin(ωt+ (j-1)π +δ?0)-

(15)

其中：

Li=|Oi,j-1Oi,j|=

(16)

如圖2所示，銑削凸曲面模具試件時，刀位點1～3位置為銑削凸曲面模具的上坡過程，刀位點4～6位置為銑削凸曲面模具的下坡過程，其切削參數和球頭銑刀參數如表1所示。根據未變形切屑厚度計算不同刀位點的切屑體積，根據UG實體造型仿真不同刀位點的切屑幾何形狀。如表2所示，切屑空間位置隨刀具前傾角的變化而變化，在刀位點1～3,4～6時，刀具前傾角在±6°～±16°之間，各位置點的切屑體積不穩定，且略有上升，在前傾角±16°附近切屑體積較大。

表1 曲面球頭銑削仿真參數Tab.1 Parameters of ball-end milling of curved surface

表2 不同刀位點前傾角及切屑UG仿真結果Tab.2 Lead angle of different positions and simulation result of UG

圖2 凸曲面模具試件及仿真位置點Fig.2 Convex surface mould and simulation position

6個刀位點上的刀工接觸區的時空特性仿真結果如圖3所示，x軸為瞬時切削位置角，用來揭示刀工接觸區的時間特征，y軸為切削層面積，用來揭示刀工接觸區的空間特征[16]。

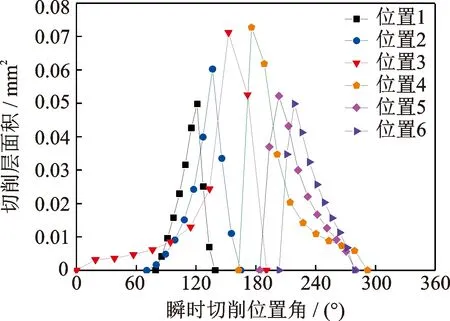
圖3 不同刀位點的單齒刀工接觸區時空特性Fig.3 Space-time characteristics of single-tooth cutter contact zone with different tool positions

從圖3中可以看出，從刀位點1～3的切削層面積逐漸減小，從刀位點4～6的切削層面積逐漸增加；在刀位點3和4、刀具前傾角為±6°左右時，此時切削層面積最大，切削力最大。凸曲面模具試件頂端刀位點的切削力最大，試件上坡位置點和下坡位置點的切削層面積呈現不對稱減小趨勢，上坡位置點的切削力明顯小于下坡位置點的切削力。 同時，從如圖3中可以看出，模具試件拼接區域的沖擊振動也引起不同刀齒的切削層面積不同，即第j齒的切削層面積增加的量和第j-1齒的切削層面積減小的量相等；考慮沖擊振動的兩個刀齒的切削層面積最大值的和不考慮沖擊振動的兩個刀齒的切削層面積最大值的和相等。

3 振動沖擊對拼接模具瞬時銑削力的影響

基于文獻[16-17]的瞬態銑削力模型和切削刃離散單元化的方法，瞬態銑削力模型由剪切力和犁耕力構成，剪切力和犁耕力分別表示瞬時切削層面積和瞬時切削刃長度的函數，球頭銑刀切削刃上離散的任意微元切向力、徑向力和軸向力表示為

(17a)

(17b)

(17c)

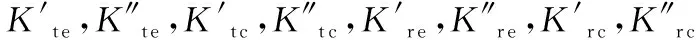
(18)

db為每一個切削刃微元所對應的切削寬度，可以表示為

(19)

由金屬切削原理可知，未變形切削厚度與切削寬度的乘積為切削層面積AD，則瞬時切削刃微元切削層面積為

Rsinθjzidθjzi

(20)

瞬時切削層面積為

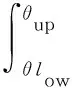
Rsinθjzidθjzi

(21)

基于文獻[18]的方法，測得不同硬度模具試件的銑削力系數。球頭銑刀銑削凸曲面時刀具前傾角不斷變化，不同刀具前傾角下的銑削力系數如圖4、圖5所示。

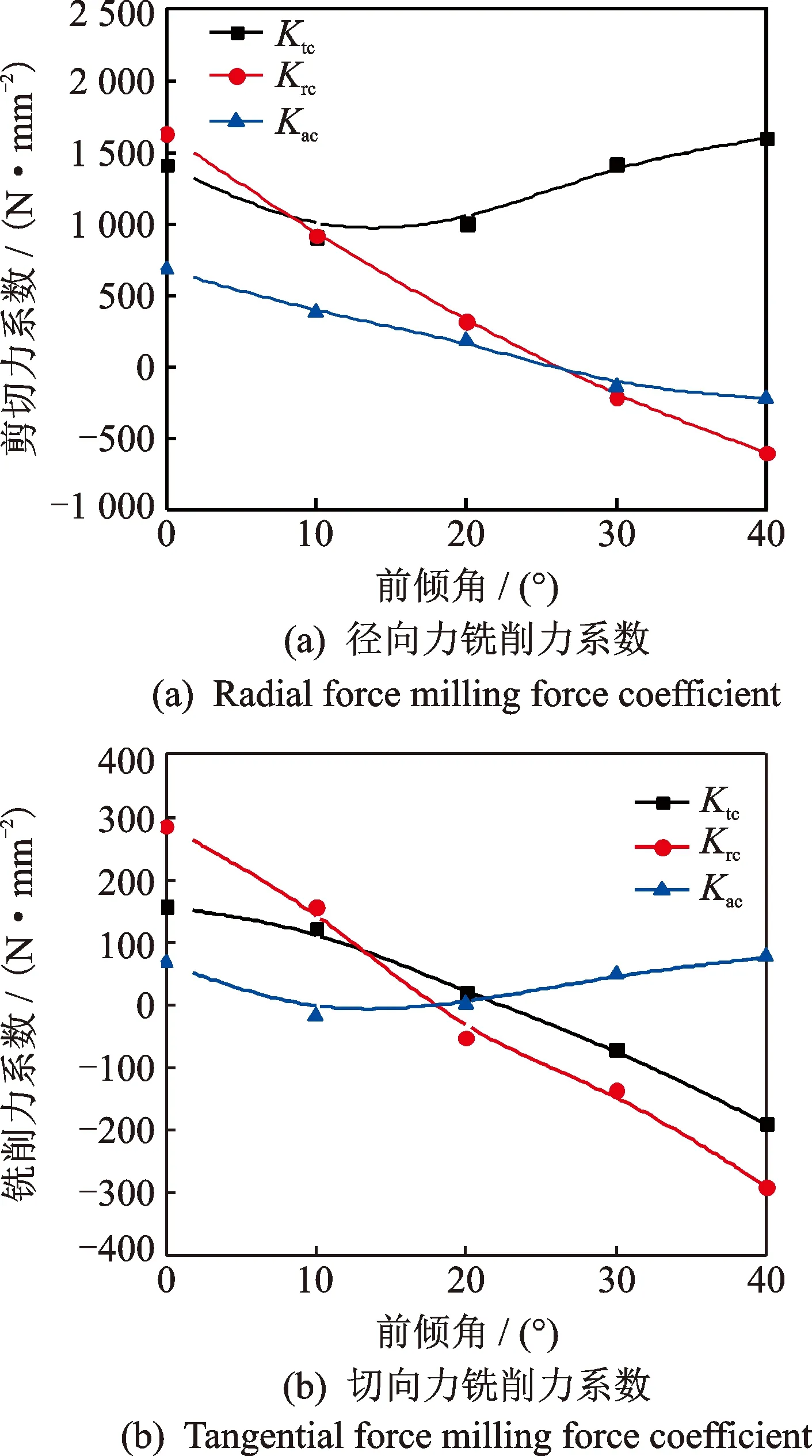
圖4 在45HRC硬度條件下刀具前傾角對銑削力系數的影響Fig.4 Effect of tool lead angle on milling force coefficients under 45HRC hardness

圖5 在60HRC硬度條件下刀具前傾角對銑削力系數的影響Fig.5 Effect of tool lead angle on milling force coefficients under 60 HRC hardness

4 凸曲面拼接區球頭銑刀瞬時銑削力實驗

加工設備為VDL-1000E型三軸立式銑床，刀具為二刃整體硬質合金球頭立銑刀；實驗樣件為不同硬度的凸曲面拼接模具試件，樣件材料為Cr12MoV模具鋼，樣件尺寸為200 mm×200 mm×60 mm，樣件分為不同硬度的3個部分，通過螺栓連接成整體，每部分硬度分別為HRC52,HRC58,HRC45。瞬時銑削力數據采集系統由Kistler9257B型測力儀、Kistler5007型電荷放大器型號、東華DH5922信號采集系統等組成，實驗樣件及測試系統布置如圖6所示。凸曲面拼接區球頭銑刀銑削采用順銑切削、切削參數如表1所示。

圖6 凸曲面淬硬鋼模具銑削現場Fig.6 Experiments of convex surface hardened steel mold

實驗過程中PCB加速度傳感器所測得的振幅值小于10 m/s2，切削平穩。切削路徑如圖2所示，切削路徑為L(P1,P2,P3,P4,P5,P6)，測得的瞬時銑削力大小如圖7所示。沖擊振動頻率由拼接區域測得的瞬時銑削力經過傅里葉變換后得到。

圖7 凸曲面拼接模具樣件的瞬時銑削力Fig.7 Instant milling force at convex surface splicing mould

在球頭銑刀銑削凸曲面拼接區過程中，由于拼接區域的沖擊振動對x和y方向的瞬時銑削力影響較大，對軸向瞬時銑削力影響相對較小，故瞬時銑削力仿真時只研究x向和y向瞬時銑削力。

當球頭銑刀從凸曲面下坡到頂端時，選取刀位點1,2,3，刀位點1位于拼接縫前，刀位點2位于拼接縫處，刀位點3位于拼接縫后，經過拼接縫時，球頭銑刀會收到了沖擊振動，在一個切削周期內進行銑削力仿真和實驗對比，如圖8～10所示。

圖8 在位置點1上瞬時銑削力的預測及實測Fig.8 Prediction and actual of milling force in position point 1

圖9 在位置點2上瞬時銑削力的預測及實測Fig.9 Prediction and actual of milling force in position point 2

圖10 在位置點3上瞬時銑削力的預測及實測Fig.10 Prediction and actual of milling force in position point 3

如圖8～10所示，發現刀位點2,3處的瞬時銑削力振蕩加強，同一個刀齒的瞬時銑削力存在分叉。刀位點1～3銑削過程中，刀具前傾角βf由大變小，刀位點x方向的銑削力Fx明顯大于y向的銑削力Fy，此時側偏角較大，為球頭刀側銑切削，x軸方向分力增加。在刀位點3處，刀具前傾角βf較小，同時工件自由曲面曲率半徑K趨近于無窮大，此時水平切觸角φ和未變形切屑厚度h(θ,φ)較大。

實驗樣件頂端兩側的銑削力由于受前傾角和側偏角的影響，x向和y向銑削力減小。由于沿著y向進給，刀具側傾角和前傾角和分別影響刀具工件接觸區相對于刀具軸線的水平切觸角和軸向切觸角的位置，導致x向和y向的瞬時銑削力Fx和的方向改變[16]。

刀位點4位于凸模頂端，既是上一個縫1的縫后，也是縫2的縫前。發現球頭銑刀經過凸模頂端時，進給方向的力反向，行距方向的力方向不變，大小略有增加，軸向力逐漸增大，到凸模頂端時軸向力最大。

如圖8～10所示，發現傾角大的切削位置，兩齒切削力的差值大，證明此時刀具受沖擊振動較大。在銑削力相同的情況下，刀具工藝系統剛度弱的位置，刀具振動明顯，同時兩齒間切削力波動增大。

當球頭銑刀從凸曲面由頂端下坡時，選取刀位點5,6，刀位點5位于拼接縫處，刀位點6位于拼接縫后，經過拼接縫時，球頭銑刀會收到了沖擊振動，在一個切削周期內進行銑削力仿真和實驗對比，如圖11、圖12所示。

圖11 在位置點5上瞬時銑削力的預測及實測Fig.11 Prediction and actual milling force in position point 5

圖12 在位置點6上瞬時銑削力的預測及實測Fig.12 Prediction and actual milling force in position point 6

如圖11,12所示，發現刀位點5,6處的瞬時銑削力同理也變得振蕩加強，同一個刀齒的瞬時銑削力有分叉。當球頭銑刀從凸曲面頂端下坡時，相比于凸曲面銑削上坡過程，刀位點5和6的刀具側偏角和行距方向曲率半徑增大，軸向切觸角的范圍增大。同時，由于球頭銑刀存在螺旋升角，任意刀齒在一個切削周期內軸向力方向會產生變化，銑削力出現正負變化，波動范圍增大。由于沖擊振動的影響，在5個刀位點上的瞬時銑削力都不相同。

總之，基于次擺線軌跡方程和沖擊振動的瞬時銑削力仿真結果與實測結果基本一致，在不同位置點上的球頭銑刀瞬時最大銑削力的預測值和實驗值的誤差如表3所示。

表3 不同位置點上的瞬時最大銑削力的預測值與實驗值之間的誤差Tab.3 Error between of the predicted value and the experimental value of the maximum milling force at different points

5 結 論

1) 球頭刀銑削中，每齒進給量與實際切削半徑的比率越大，三維次擺線軌跡對未變形切屑厚度的影響越大；距離刀尖越近的微元，刀具振動越大；球頭銑刀的瞬時銑削力預測需要基于刀齒三維次擺線運動軌跡方程，同時考慮球頭銑刀振動的影響。

2) 當球頭銑刀的前傾角最小時，切屑體積最大，瞬時銑削力最大，瞬態變化復雜；銑削凸曲面模具上坡時銑削力平穩性要好于下坡時銑削力平穩性；切屑空間位置隨刀具前傾角的變化而變化，刀具前傾角在±6°～±16°之間，各位置點的切屑體積不穩定，且略有上升，在前傾角±16°附近切屑體積較大，兩齒銑削力差值較大，刀具受沖擊振動較大，加工穩定性下降。

3) 當球頭銑刀從凸曲面頂端下坡時、從凸曲面下端到頂端上坡時，經過拼接縫時都受到沖擊振動，使拼接區域的瞬時銑削力振蕩加強，同一個刀齒的銑削力有分叉現象，這是由于在過縫處產生的沖擊力震蕩衰減所影響的。在上坡時，x方向的銑削力Fx明顯大于y向銑削力Fy，此時側偏角較大，為球頭刀側銑切削，x軸方向分力增加。進給方向(y方向)銑削力Fx明顯增大。在下坡時，刀具側偏角和行距方向曲率半徑增大，軸向切觸角的范圍增大，同時，銑削力出現正負變化，波動范圍增大。

4) 實驗結果表明，瞬時銑削力預測值和實驗測量值在幅值上和周期變化趨勢上具有一致性，在平穩切削時最大瞬時銑削力的預測誤差值基本在15%以內。考慮球頭銑刀過拼接縫時沖擊振動對凸曲面模具銑削力的影響，有益于拼接區域的加工誤差及表面形貌預測。