共振碎石機振動機理及參數研究

李吉祥，范晨光，李彥達

(西南交通大學 力學與工程學院，四川 成都 611756)

0 引言

水泥路面共振碎石化技術是舊水泥路面碎石化改造及再生利用的一項關鍵工程技術。由于其高效環保的施工特點，已經成為目前舊水泥路面最有效的改造方法。作為共振破碎機進行碎石作業的核心系統，共振系統工作端的響應輸出受共振梁各結構參數、激振器頻率及激振力大小等因素的影響。在共振系統的設計過程中，可以通過控制共振系統結構參數的方法來控制系統頻率及響應。因此，針對共振系統的力學建模和理論分析，可以加深對共振碎石化機械工作原理和系統性能的認識。

隨著對混凝土路面的大量修復的需要，共振碎石化技術的自主研發和產業化需求日益迫切。美國的共振機械有限公司(RMI)是目前國際上唯一掌握共振碎石化核心技術并研發出共振式道路破碎機用于現場施工的企業。1980年，Raymond等[1-2]申請了共振試驗臺架的專利，對共振式道路破碎機共振梁的支撐節點位置及激振頻率展開研究，并申請了共振式道路破碎機的發明專利。國內研究起步較晚。徐海[3]結合多體系統動力學理論知識，運用虛擬樣機技術，對共振破碎機振動系統進行了動力學仿真研究。Zhang等[4]基于共振式路面破碎車共振系統的結構，給出了破碎機的共振頻率和振幅的參數模型。基于比例泵空馬達，建立了頻率調節的控制模型，針對共振系統模型中的不確定參數設計了一套自適應的算法，從而得出各個參數的自適應規律，利用Lyapunov函數，驗證了頻率的輸入的規律。李萬莉等[5]通過經典力學方法在理論上建立了共振梁受迫振動的動力學模型，并利用振型疊加法對此動力學方程進行求解，但并沒有給出求解結果及各項系統參數對共振頻率的影響。黃家善等[6]釆用控制器得到了破碎機的電氣系統。晏星凡[7]以反求理論為理論基礎，運用多剛體多力學、智能優化和有限元等技術，對破碎機的振動系統進行了反求仿真分析，獲得了1組設計參數，在這組參數下，動力學模型的分析結果跟原型機結果相近，并且能滿足平順性要求。紀秀業[8]借助仿真分析技術，對共振破碎機的車架結構進行設計研究，進一步完善了對車架的優化設計。王曉友[9]建立了剛柔耦合的虛擬樣機模型，研究了整梁柔性化和分段柔性化對振動特性的影響，并研究了激振器不同的頻率時路面的響應特性。李盛等[10]研究了不同頻率和行進速度對共振碎石化整體破碎效果的影響，發現共振破碎機行進速度對破碎粒徑大小、回彈模量和彎沉值的大小均有影響。

比較來看, 國內對共振碎石化技術的研究并不深入，雖然部分企業開始了共振碎石化機械的應用，但是一直還處在道路施工技術摸索階段[11-18]，目前尚缺乏對共振系統振動機理及其參數控制的完整動力學理論分析及參數研究的文獻報道。本研究根據共振碎石化機械的特點，建立共振系統的動力學模型，并推導其運動微分方程，利用假設模態法離散，計算系統固有頻率及強迫振動響應，研究各系統參數對固有特性及響應特性的影響。

1 共振系統運動方程的建立

1.1 共振系統的模型及簡化

共振破碎機通過控制激振端的振動頻率，使共振大梁帶動錘頭產生振動。當振動頻率等于或接近水泥混凝土路面的固有頻率時，在錘頭作用下，激勵路面板塊產生共振，當混凝土路面強迫響應超過混凝土顆粒間最大摩擦力時，混凝土內部產生剪切破環，從而達到破碎路面的效果。目前，常用的共振碎石化機械的共振系統結構簡圖如圖1所示[3]。

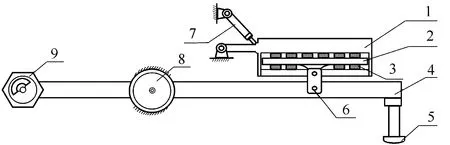
1—配重體; 2—承載體; 3—減振材料; 4—共振梁; 5—碎錘頭;6—吊耳;7—舉升油缸; 8—橡膠減震器; 9—激振器圖1 共振結構示意圖Fig.1 Schematic diagram of resonance structure

由于共振大梁振動時產生彎曲變形，為方便動力學方程建模，做出如下簡化[3]:

(1)將共振梁視為等截面梁。忽略吊耳及橡膠減振器部位的鉸接孔對梁橫向彎曲剛度的影響。

(2)忽略激振器及錘頭的細節，將其簡化為集中質量塊，分別位于共振梁的兩邊。

(3)與共振梁連接的支承部分簡化為彈簧。

簡化后的動力學模型如圖2所示，Fsin(wt)為外激勵，激振器和破碎錘頭分別簡化為共振梁兩端的集中質量m1及m2，共振大梁支承部分簡化為彈簧，等效剛度分別為k1,k2，在錘頭端的等效彈簧處加一阻尼器，阻尼系數為c。以m1為原點建立坐標系，共振大梁總長度為l，a為原點到第1個彈簧的距離，b為原點到第2個彈簧的距離。

圖2 簡化后的共振系統動力學模型Fig.2 Simplified dynamic model of resonance system

1.2 共振系統的動力學方程推導

結合實際的共振碎石機，將系統的振動分為兩部分，分別為剛體振動和彈性體振動。共振系統的動力學方程應同時包含兩部分的振動。首先計算剛體振動階段的固有頻率和模態，再通過假設模態法離散系統方程，最后計算響應。

1.2.1剛體振動固有頻率的推導與計算

共振系統的剛體振動分為剛體平移和剛體轉動兩部分。設系統做剛體平移的豎向位移為xd，做剛體轉動的角度為θ，C為共振梁的質心，如圖3所示。

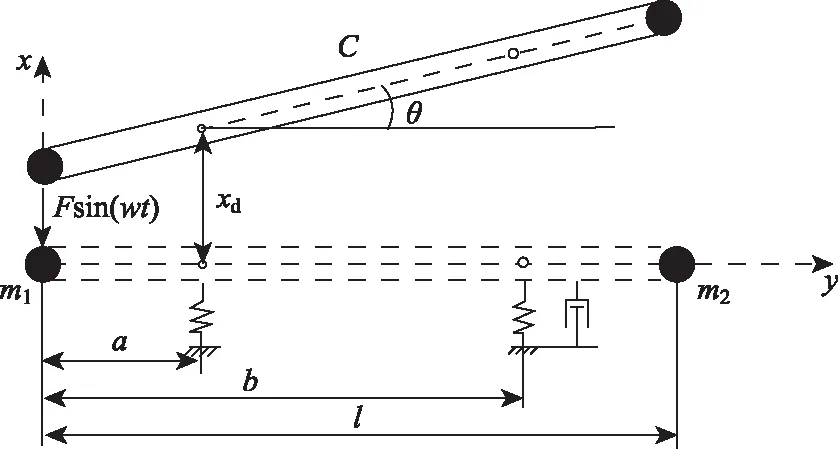
圖3 共振梁的剛體振動示意圖Fig.3 Schematic diagram of rigid body vibration of resonance beam

考慮梁上的附加質量及彈性支撐，系統做剛體振動的動能及勢能可表示為：

(1)

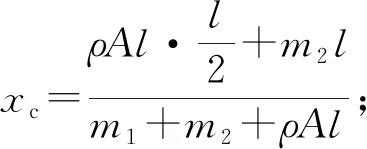
由拉格朗日方程，

(2)

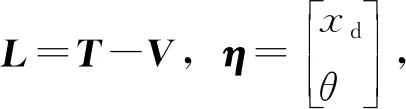
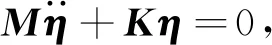
(3)

式中，

將式(2)整理成標準特征值問題可得：

|K-ω2M|ψ=0。

(4)

通過特征值分析，即可求出系統做剛體振動時的兩階固有頻率ω及模態ψ，分別為ω1和ω2，ψ1和ψ2。

1.2.2共振系統運動方程

設y(x,t)為梁的橫向位移，梁上作用有單位長度分布力q(x,t)，根據文獻[10]得到系統橫向振動偏微分方程為：

(5)

式中EI為共振大梁的抗彎剛度。

設共振梁的第i階振型函數為ψi(x)，系統的響應可表示為：

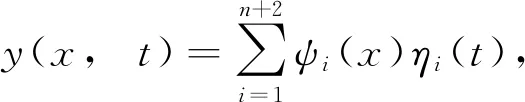
(6)

式中,ηi(t)為廣義坐標，當i=1，2時，ψ1和ψ2是上一小節中計算得到的剛體振動階段的模態,η1(t)，η2(t)為相應的廣義坐標。當i≥3時，假設其模態為兩端自由梁的模態[18]，表示為：

(7)

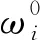
然后列出系統共振運動時的動能和勢能為：

(8)

將系統響應代入整理可得：

(9)

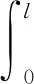
由于結構一旦確定且材料不變的情況下，結構阻尼的變化是十分小的，所以為了研究阻尼比對共振大梁的影響，在錘頭端彈簧處加有一個阻尼器，其阻尼系數定為c1，以此作為整個系統的阻尼。所以阻尼矩陣即可表示為：

C=c1ψT(b)ψ(b)。

(10)

采用式(5)離散后的系統運動方程的一般矩陣形式：

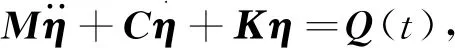
(11)

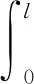
激振器通過偏心質量塊旋轉產生激振力。激振力F的大小可表示為[3]:

F=meω2，

(12)

式中，e為轉子質心的偏心半徑；m為轉子的質量；ω為外激勵頻率。

由于激振力是作用于梁激振端的集中力，故需要將集中力轉變為分布力進行表示。引入狄拉克函數δ(x-xi)，其中xi為集中力作用點的坐標，則廣義力表示為：

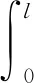
(13)

由此，將連續系統振動問題離散為多自由度系統振動問題。

2 系統響應求解

(K-ω2M)κ=0。

(14)

解得ωi為系統第i階固有頻率，κi為對應特征向量。

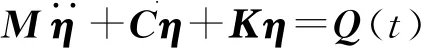
(15)

式中第i個方程為：

(16)

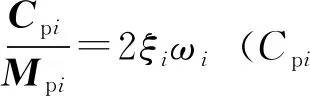
(17)

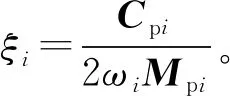
又因為Qi(t)=Pi(t)sin(ωt)，其中Pi(t)為同一頻率的簡諧激振力，所以式(15)可寫為：

(18)

由單自由度強迫振動的結論，主坐標下的穩態解為：

(19)

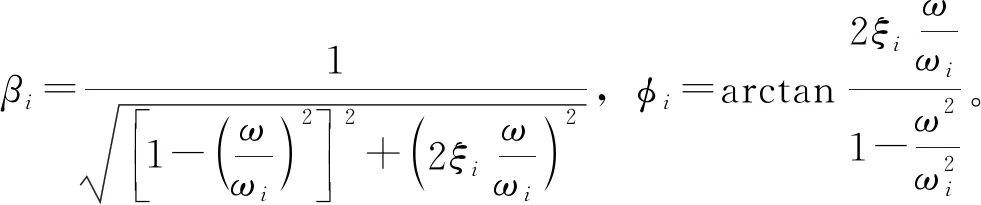
所以，可以得到：

(20)

系統的響應為：

ψ2η2。

(21)

3 計算結果分析

3.1 系統固有頻率計算

根據文獻[3]中數據進行計算：振動梁長度l=3.85 m，截面寬b=0.5 m，截面高h=0.15 m，激振端集中質量m1=300 kg；錘頭集中質量m2=100 kg；材料彈性模量E=2.1×1011Pa；材料密度ρ=7 850 kg/m3；激振器參數，轉子質心半徑e=56 mm；轉子質量m=23 kg；激振頻率35～53 Hz。在滿足精度要求的前提下，為簡化計算，取n=5。

共振碎石機工作過程中，要求錘頭的振動頻率為35～53 Hz。當共振碎石機的固有頻率與激振力的頻率相近時，才能實現共振碎石機的最佳工作狀態。由式(12)求得系統前5階固有頻率，如表1 所示。

由表1可以發現，固有頻率與文獻[3]中對比，低階誤差很小，在5階頻率開始出現誤差，考慮是由于模態選取數量較少產生的誤差，由于共振碎石機的工作頻率在35～53 Hz之間，故可忽略高階頻率的誤差。此外，系統做剛體振動時的固有頻率非常小，實際的振動過程中以彈性振動為主，與文獻[10]對比后發現，共振碎石機頻率和行進速度較佳組合為：振動頻率為48 Hz，共振時行進速度為1.3 km/h。與計算結果的43.06 Hz誤差不大，較為可信。

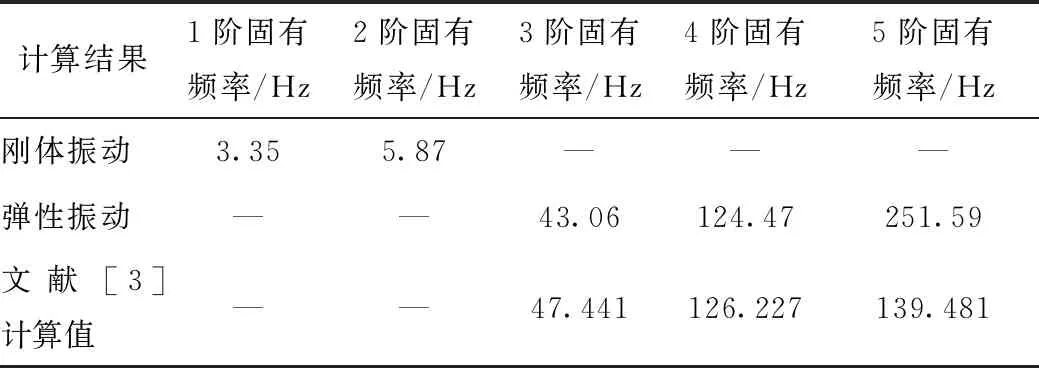
表1 系統前5階固有頻率Tab.1 First 5 natural frequencies of system

3.2 系統參數對固有頻率的影響

共振系統的頻率與系統的結構參數有密切關系。通過改變系統結構參數，可以對系統固有頻率進行控制。共振大梁截面高度及寬度、激振端質量、錘頭端質量、激振端和錘頭端減振器等效剛度等都可能會對系統固有頻率產生影響。圖4(a)～(f)分別給出了各個參量對系統的固有頻率的影響。

可以看出，共振梁截面高度及寬度、激振端質量、錘頭端質量、激振端和錘頭端減振器等效剛度等參數都會對系統固有頻率產生影響。其中，系統各階固有頻率隨著共振梁截面寬度、截面高度的增大而增大，隨著激振端質量、錘頭質量的增大而減小；增大激振端減振器等效剛度，系統各階固有頻率增大；增大錘頭端減振器等效剛度，系統各階固有頻率也將增大。對比可見，共振梁截面高度的變化對系統模態的影響最為顯著，可以通過控制共振梁截面高度來有效改變梁的各階頻率。

3.3 外界激振頻率對錘頭端振幅的影響

激振力的頻率及大小是由激振器提供的。改變激振器激振頻率會引起錘頭振幅的改變。選取了兩階剛體模態及第3階彈性體模態所求得的錘頭端響應關系，并且使用不同的彈簧減震器剛度值進行對比，如圖5所示。

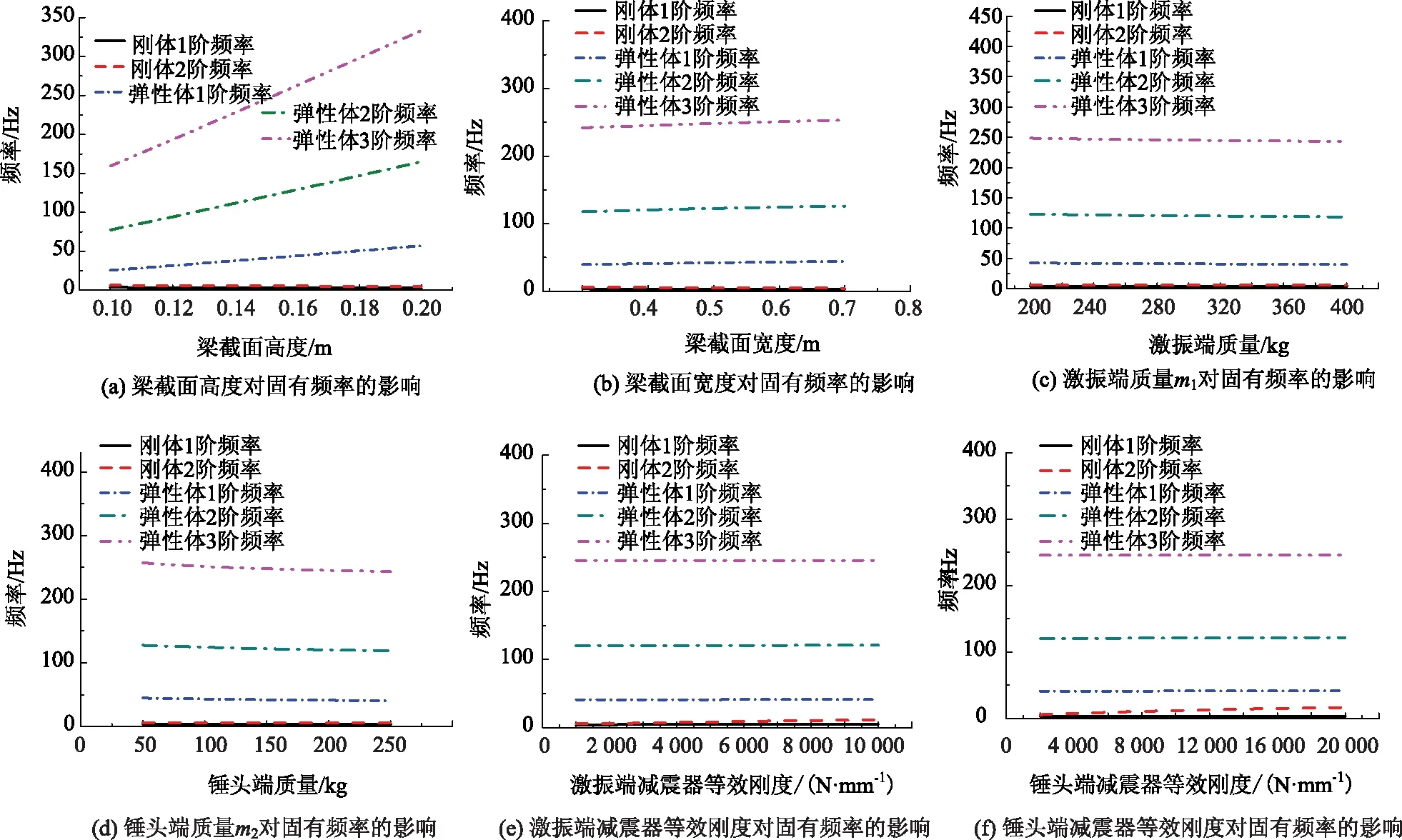
圖4 系統結構參數對固有頻率的影響Fig.4 Influence of system structure parameters on natural frequency

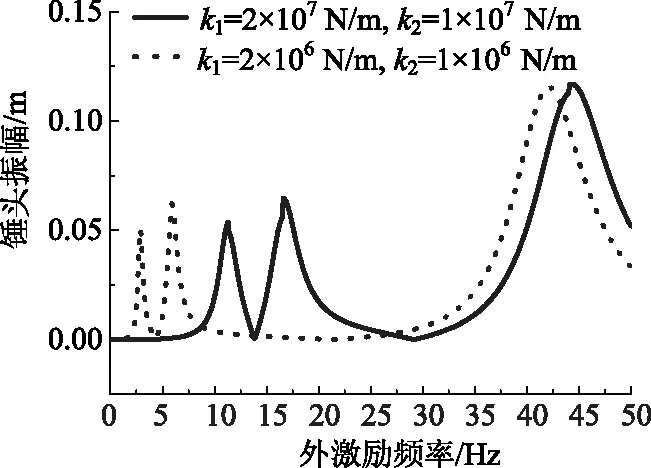
圖5 外激勵頻率與錘頭振幅的關系曲線Fig.5 Curves of external excitation frequency vs. hammerhead amplitude

在激振器結構確定的情況下，激振力的頻率逼近系統固有頻率時，錘頭振幅變大。所以在激振力頻率接近系統固有頻率的情況下，對能量的利用更為高效。

3.4 阻尼系數對錘頭端振幅的影響

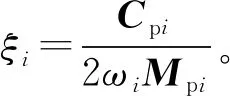
圖6為系統以彈性振動1階固有頻率發生共振時的共振大梁阻尼系數取值與錘頭振幅的關系。可以看出，隨著阻尼系數的增大，錘頭的振幅也逐漸變小，與阻尼影響振動衰減一致。

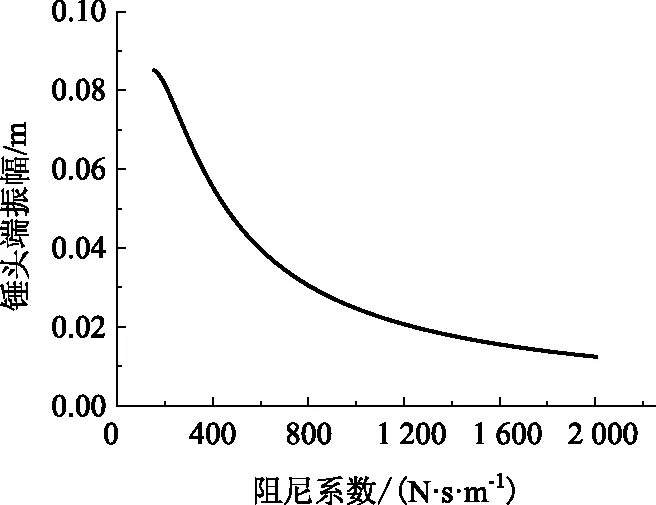
圖6 阻尼器的阻尼系數與錘頭振幅的關系曲線Fig.6 Curve of damping coefficient of damper vs. hammerhead amplitude

4 結論

本研究從共振大梁的剛體振動和彈性振動出發，建立了共振碎石機共振大梁的動力學模型。基于假設模態法，求解了系統參數對其固有頻率及強迫響應的影響，對工程應用上更好地理解共振碎石機的振動原理起到了積極的作用，填補了目前共振碎石機振動機理理論計算的空白，著重研究了系統參數對共振頻率的影響，結論如下：

(1)在本研究的參數下，系統做剛體振動時的固有頻率分別為3.35，5.87 Hz，不在共振碎石機的工作頻率范圍內，計算獲得的工作頻率為43.06 Hz，發生在彈性振動階段，共振大梁的梁高在0.1～0.16 m 區間內時為最佳工作頻率，有助于工程應用中控制共振梁的固有頻率。

(2)當外激勵頻率接近共振大梁的固有頻率時發生共振，錘頭的振幅會變大，且彈簧剛度越大，發生共振的頻率越高，此時對能量的利用率更為高效。

(3)阻尼系數在200～2 000 (N·s)/m范圍內變化時，最大錘頭振幅為0.084 m，其對錘頭振幅的影響呈反比趨勢，與阻尼影響振動衰減一致。